I2P: Signature and Signature Verification EdDSA
In a previous article , we examined the implementation of the Ed25519 curve itself, the operations of addition and multiplication by a number, and the restoration of the second coordinate. This article discusses the effective use of these operations for electronic signature of messages and work in I2P.
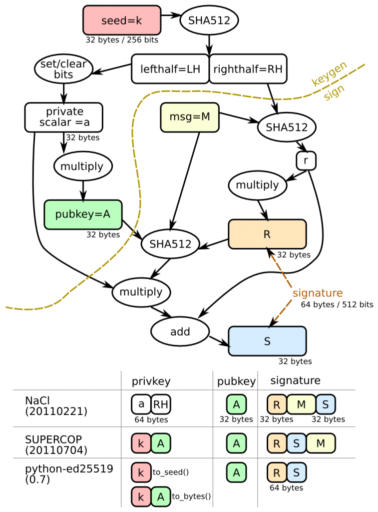
Unlike RSA, where the secret and public key can be used directly, here you have to use a more complex scheme and enter some additional object. EdDSA conceptually implements the DSA algorithm , extending it to the case of curves. The signature is a pair of numbers (R, S), for EdDSA each is 32 bytes long, total the length of the signature is 64 bytes. Not the data itself is signed, but a hash of it. As a hash function, SHA512 is used. Next, small letters will denote numbers, and in capital letters the corresponding point on the curve obtained by multiplying the number by the base point B.
Let h be the hash of the message to be signed, a be the secret key, and A the corresponding public key (A = a * B). Take a random number r, and calculate R = r * B and s = r + h * a. The pair (R, s) will be a signature, where R is represented by its y coordinate.
When verifying the signature, the recipient knows A and h and it is necessary to verify the truth of (R, s). To do this, verify the equality: s * B = R + h * A.
Indeed (r + h * a) * B = r * B + h * a * B = R + h * A.
Note that s is calculated directly on the basis of the secret key, and not the point it generated, because errors in the implementation can lead to its immediate compromise. In particular, the unsuccessful choice of r. To avoid this, Bernstein suggests calculating r as a hash from half the hash of the secret key combined with the signed data itself, however, choosing r in some other way will not interfere with the algorithm, that is, the signature values themselves will be different, but the result of the verification will be the same. We will calculate r, as Bernstein suggests and how it is done in the official I2P.
For further calculations, a previously unused curve parameter l =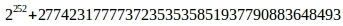 , such that l * B = 0, will be required .
, such that l * B = 0, will be required .
It immediately follows from this equality that the values of the factor in front of the point should not exceed l, otherwise this will only lead to an increase in the amount of computation. If the factor exceeds l, then it must be taken modulo, in particular, the value of h, which is a 64-byte SHA512 hash.
From this, in turn, it follows that the multiplier in the multiplication operation does not exceed 32 bytes and the most significant bit is always zero.
As can be seen from the formulas, a signature requires one multiplication by a base point, and to verify a signature, two: one by a base point, and the second by a public key.
For the base point, it makes sense to calculate the result of multiplying by different factors in advance. The simplest is a series (B, 2 * B, 4 * B, 8 * B, ...) of only 255 points, which allows eliminating the doubling operation at each step. You can go further and expand the factor not in powers of two, but in powers of 16, and for every 4 bits of the factor add the calculated point from the array to the result. To do this, you need to calculate and store 32 * 2 * 16 points, but this is done once for the duration of the work. Thus, the multiplication by B reduces exactly to 64 additions and the message is signed quickly. This is how it looks in code.
Here Bi16 is an array of 64x16 points, and e is a 32-byte multiplier in Little Endian. Instead of powers of 16, expansions in powers of 256 can be used, this will lead to some acceleration, at the same time it will be necessary to store 32 * 256 points already.
To verify the signature, we need to multiply the public key as well, although it is the result of multiplying B, we do not know the multiplier, since this is the secret key. If you apply this method, you will have to keep such an array for each of them, and there are a lot of public keys in I2P - there is a separate key for each node from netdb, of which there are about several thousand, which would lead to unjustified memory consumption. Therefore, in order to achieve a work speed comparable to other elliptical curves, it is necessary to improve the addition operation.
As noted in a previous article , the slowest operation is division at each addition, which you can get rid of by going to uniform coordinates. The implementation becomes less obvious, but all implementations of elliptical cryptography are arranged there. Instead of the two coordinates of the point (x, y), a third coordinate is entered that stores the common denominator, and instead of x and y their numerators are stored, that is, from the homogeneous coordinates (X, Y, Z), the true coordinates are obtained as (X / Z, Y / Z ) In addition, the fourth coordinate T = X * Y / Z is entered. The coordinates of the addition result are calculated by the following formulas:
X = (X1 * Y2 + Y1 * X2) * (Z1 * Z2-d * T1 * T2)
Y = (Y1 * Y2 + X1 * X2) * (Z1 * Z2 + d * T1 * T2)
Z = (Z1 * Z2-d * T1 * T2) * (Z1 * Z2 + d * T1 * T2)
T = (Y1 * Y2 + X1 * X2) * (X1 * Y2 + Y1 * X2)
As you can see, the time-consuming operation of raising to a power in the process of addition and multiplication is no longer applied.
Another disadvantage of homogeneous coordinates is the complexity of comparing two points: the X and Y coordinates cannot be directly compared - they need to be brought to a common denominator in one way or another, which requires additional calculations. To verify the signature, you need to compare the points.
We rewrite the expression for verifying the signature s * B = R + h * A in the form R = s * Bh * A.
Then, instead of restoring the X coordinate of the point from the Y coordinate from the signature, you can take the Y coordinate from (s * Bh * A), thereby saving another exponentiation and comparing numbers instead of points. This method requires a subtraction operation, which is implemented through addition and unary minus, defined as (-X, Y, Z, -T). Thus, the subtraction operation is performed at the same speed as the addition, and can be used for expansion in degrees with negative coefficients, which reduces the memory size by 2 times.
The length of the I2P address with EdDSA is 391 bytes, the signature type code is 7, it is indicated in the documentation as EdDSA_SHA512_Ed25519.
The length of the secret and public keys is 32 bytes, the signature length is 64 bytes, the first 32 bytes are R in the form of the y coordinate, the second 32 bytes are s.
All numbers are transferred to Little Endian.
EdDSA is currently the recommended signature type for RouterInfo.
Thus, two articles describe the full and transparent implementation of EdDSA on top of the library for working with large numbers from the openssl library, working at high speed and practically used in i2pd .
EdDSA Signature Algorithm
Unlike RSA, where the secret and public key can be used directly, here you have to use a more complex scheme and enter some additional object. EdDSA conceptually implements the DSA algorithm , extending it to the case of curves. The signature is a pair of numbers (R, S), for EdDSA each is 32 bytes long, total the length of the signature is 64 bytes. Not the data itself is signed, but a hash of it. As a hash function, SHA512 is used. Next, small letters will denote numbers, and in capital letters the corresponding point on the curve obtained by multiplying the number by the base point B.
Let h be the hash of the message to be signed, a be the secret key, and A the corresponding public key (A = a * B). Take a random number r, and calculate R = r * B and s = r + h * a. The pair (R, s) will be a signature, where R is represented by its y coordinate.
When verifying the signature, the recipient knows A and h and it is necessary to verify the truth of (R, s). To do this, verify the equality: s * B = R + h * A.
Indeed (r + h * a) * B = r * B + h * a * B = R + h * A.

Note that s is calculated directly on the basis of the secret key, and not the point it generated, because errors in the implementation can lead to its immediate compromise. In particular, the unsuccessful choice of r. To avoid this, Bernstein suggests calculating r as a hash from half the hash of the secret key combined with the signed data itself, however, choosing r in some other way will not interfere with the algorithm, that is, the signature values themselves will be different, but the result of the verification will be the same. We will calculate r, as Bernstein suggests and how it is done in the official I2P.
Effective Multiplication Implementation
For further calculations, a previously unused curve parameter l =
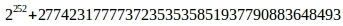 , such that l * B = 0, will be required .
, such that l * B = 0, will be required . It immediately follows from this equality that the values of the factor in front of the point should not exceed l, otherwise this will only lead to an increase in the amount of computation. If the factor exceeds l, then it must be taken modulo, in particular, the value of h, which is a 64-byte SHA512 hash.
From this, in turn, it follows that the multiplier in the multiplication operation does not exceed 32 bytes and the most significant bit is always zero.
As can be seen from the formulas, a signature requires one multiplication by a base point, and to verify a signature, two: one by a base point, and the second by a public key.
For the base point, it makes sense to calculate the result of multiplying by different factors in advance. The simplest is a series (B, 2 * B, 4 * B, 8 * B, ...) of only 255 points, which allows eliminating the doubling operation at each step. You can go further and expand the factor not in powers of two, but in powers of 16, and for every 4 bits of the factor add the calculated point from the array to the result. To do this, you need to calculate and store 32 * 2 * 16 points, but this is done once for the duration of the work. Thus, the multiplication by B reduces exactly to 64 additions and the message is signed quickly. This is how it looks in code.
EDDSAPoint res {zero, one};
for (int i = 0; i < 32; i++)
{
uint8_t x = e[i] & 0x0F; // 4 low bits
if (x > 0)
res = Sum (res, Bi16[i*2][x-1], ctx);
x = e[i] >> 4; // 4 high bits
if (x > 0)
res = Sum (res, Bi16[i*2+1][x-1], ctx);
}
Here Bi16 is an array of 64x16 points, and e is a 32-byte multiplier in Little Endian. Instead of powers of 16, expansions in powers of 256 can be used, this will lead to some acceleration, at the same time it will be necessary to store 32 * 256 points already.
To verify the signature, we need to multiply the public key as well, although it is the result of multiplying B, we do not know the multiplier, since this is the secret key. If you apply this method, you will have to keep such an array for each of them, and there are a lot of public keys in I2P - there is a separate key for each node from netdb, of which there are about several thousand, which would lead to unjustified memory consumption. Therefore, in order to achieve a work speed comparable to other elliptical curves, it is necessary to improve the addition operation.
Addition in homogeneous coordinates
As noted in a previous article , the slowest operation is division at each addition, which you can get rid of by going to uniform coordinates. The implementation becomes less obvious, but all implementations of elliptical cryptography are arranged there. Instead of the two coordinates of the point (x, y), a third coordinate is entered that stores the common denominator, and instead of x and y their numerators are stored, that is, from the homogeneous coordinates (X, Y, Z), the true coordinates are obtained as (X / Z, Y / Z ) In addition, the fourth coordinate T = X * Y / Z is entered. The coordinates of the addition result are calculated by the following formulas:
X = (X1 * Y2 + Y1 * X2) * (Z1 * Z2-d * T1 * T2)
Y = (Y1 * Y2 + X1 * X2) * (Z1 * Z2 + d * T1 * T2)
Z = (Z1 * Z2-d * T1 * T2) * (Z1 * Z2 + d * T1 * T2)
T = (Y1 * Y2 + X1 * X2) * (X1 * Y2 + Y1 * X2)
As you can see, the time-consuming operation of raising to a power in the process of addition and multiplication is no longer applied.
Another disadvantage of homogeneous coordinates is the complexity of comparing two points: the X and Y coordinates cannot be directly compared - they need to be brought to a common denominator in one way or another, which requires additional calculations. To verify the signature, you need to compare the points.
Subtraction of two curve points
We rewrite the expression for verifying the signature s * B = R + h * A in the form R = s * Bh * A.
Then, instead of restoring the X coordinate of the point from the Y coordinate from the signature, you can take the Y coordinate from (s * Bh * A), thereby saving another exponentiation and comparing numbers instead of points. This method requires a subtraction operation, which is implemented through addition and unary minus, defined as (-X, Y, Z, -T). Thus, the subtraction operation is performed at the same speed as the addition, and can be used for expansion in degrees with negative coefficients, which reduces the memory size by 2 times.
I2P Addresses with EdDSA
The length of the I2P address with EdDSA is 391 bytes, the signature type code is 7, it is indicated in the documentation as EdDSA_SHA512_Ed25519.
The length of the secret and public keys is 32 bytes, the signature length is 64 bytes, the first 32 bytes are R in the form of the y coordinate, the second 32 bytes are s.
All numbers are transferred to Little Endian.
EdDSA is currently the recommended signature type for RouterInfo.
Thus, two articles describe the full and transparent implementation of EdDSA on top of the library for working with large numbers from the openssl library, working at high speed and practically used in i2pd .
