"Let me explain: or why a programmer needs a mathematician." A book about how not to be bored in math lectures
TL; DR A small book about mathematics for programmers. Electronic and paper version of the link .
I have been teaching at universities for 9 years. During this time, students have changed. My subjective impression - a modern freshman appreciates his time much more strongly. In the conditions of free attendance, even excellent students should be sure that a particular lecture will bring them benefits comparable to 1.5 hours on Kaggle or Coursera. It seems that the availability of guaranteed qualitative explanations already kills the classic lecture format.. Therefore, the second lecture of the course for many lecturers usually takes place in front of a significantly smaller audience. In a smaller audience, students have a larger maneuver for questions, and the most frequent question that I heard on pairs in algorithms and discretes is “Why?”.
Why combinatorial formulas? What is the catch of all these conditional probabilities, which are usually explained on baskets and balls? Why multiply matrices? And why are inverse matrices necessary? Well, ok, here's the search in width, and what?
Not to say that during my own IT-students I received distinct answers to all these questions. But experience in companies of completely different types partially brought me closer to understanding. On my own pairs, I try to give examples not on cats, to build not obvious analogies, and generally somehow bring the industry closer to mathematics. At the same time, the total audience of all my occupations over the years hardly passed for 1000 people. So I came up with a bunch of explanations and a book with examples for programmers.
Below I give a little fragment. You can get a book in paper or electronic form,by clicking on the link . Feedback is welcome! They drove.
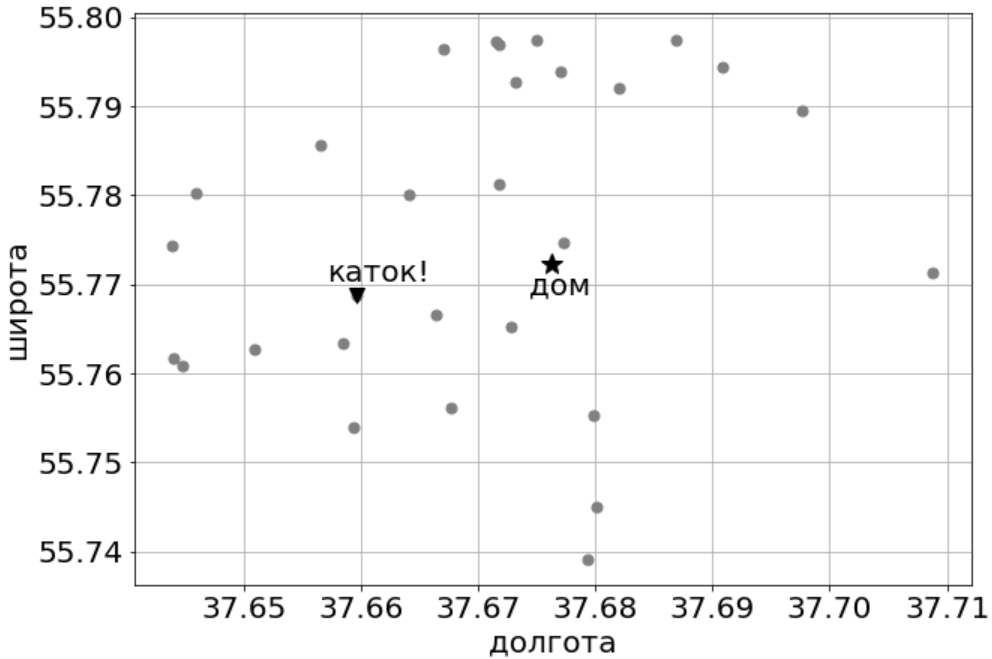
Moscow. It's winter, not very cold, sunny. Sunday morning. You have passed the test or even the exam on linear algebra, and you have your own skates. What else is needed for happiness?
You want a skating rink!
For a cup of tea you have developed a plan. You are interested in skating rinks that are fairly close to home, but this is not enough, you need more amenities. Better to let these rollers be free, with Wi-Fi and a toilet.
You named a lot of similar roller A , and user-friendly - Bed and . And since we are interested in, and the proximity and convenience, our goal - the intersection of the sets A ∩ Bed and . Where do we get these sets?
Going through sites rinks or read reviews "Posters" - not your method. Therefore, you go to the portalMoscow’s open data , or rather, for you, this is done by a Python script, an example of which can be found on the book’s website in document M02 - vectors (skating) . You find that there are a lot of skating rinks in Moscow - 1350. How are we going to search? Here you remember the textbook on linear algebra and understand that you need to map the rollers into two signs you need: a two-dimensional coordinate (latitude, longitude) and three-dimensional — convenience (Wi-Fi, toilet, free of charge) .
In the second space, the presence of a sign will be one, and the absence will be zero, which means that it is no longer necessary to rationalize these data. We will not normalize the coordinates either, since they are comparable in our latitudes (otherwise, we would have to choose a reference point and convert degrees to meters). And then choose only the most interesting options - why do you need a skating rink, which is on the other side of the city or in which there are obviously no amenities? For any of the spaces, we will take only the data with the smallest Euclidean distance to the target.
All is ready. It remains only to peek somewhere our own coordinates (now this can be done in any application with maps) and find all the suitable rollers at the
intersection of the sets A and B :
For the data from the example, among the 30 nearest skating rinks we get one skating rink on the Old Basmannaya, but with all the conveniences. And you can even walk.
Try using the Moscow open data portal to independently find the open Wi-Fi closest to you, a summer cinema or courtyard surveillance cameras.
I have been teaching at universities for 9 years. During this time, students have changed. My subjective impression - a modern freshman appreciates his time much more strongly. In the conditions of free attendance, even excellent students should be sure that a particular lecture will bring them benefits comparable to 1.5 hours on Kaggle or Coursera. It seems that the availability of guaranteed qualitative explanations already kills the classic lecture format.. Therefore, the second lecture of the course for many lecturers usually takes place in front of a significantly smaller audience. In a smaller audience, students have a larger maneuver for questions, and the most frequent question that I heard on pairs in algorithms and discretes is “Why?”.
Why combinatorial formulas? What is the catch of all these conditional probabilities, which are usually explained on baskets and balls? Why multiply matrices? And why are inverse matrices necessary? Well, ok, here's the search in width, and what?
Not to say that during my own IT-students I received distinct answers to all these questions. But experience in companies of completely different types partially brought me closer to understanding. On my own pairs, I try to give examples not on cats, to build not obvious analogies, and generally somehow bring the industry closer to mathematics. At the same time, the total audience of all my occupations over the years hardly passed for 1000 people. So I came up with a bunch of explanations and a book with examples for programmers.
Below I give a little fragment. You can get a book in paper or electronic form,by clicking on the link . Feedback is welcome! They drove.
Moscow skating rinks
Moscow. It's winter, not very cold, sunny. Sunday morning. You have passed the test or even the exam on linear algebra, and you have your own skates. What else is needed for happiness?
You want a skating rink!
For a cup of tea you have developed a plan. You are interested in skating rinks that are fairly close to home, but this is not enough, you need more amenities. Better to let these rollers be free, with Wi-Fi and a toilet.
You named a lot of similar roller A , and user-friendly - Bed and . And since we are interested in, and the proximity and convenience, our goal - the intersection of the sets A ∩ Bed and . Where do we get these sets?
Going through sites rinks or read reviews "Posters" - not your method. Therefore, you go to the portalMoscow’s open data , or rather, for you, this is done by a Python script, an example of which can be found on the book’s website in document M02 - vectors (skating) . You find that there are a lot of skating rinks in Moscow - 1350. How are we going to search? Here you remember the textbook on linear algebra and understand that you need to map the rollers into two signs you need: a two-dimensional coordinate (latitude, longitude) and three-dimensional — convenience (Wi-Fi, toilet, free of charge) .
In the second space, the presence of a sign will be one, and the absence will be zero, which means that it is no longer necessary to rationalize these data. We will not normalize the coordinates either, since they are comparable in our latitudes (otherwise, we would have to choose a reference point and convert degrees to meters). And then choose only the most interesting options - why do you need a skating rink, which is on the other side of the city or in which there are obviously no amenities? For any of the spaces, we will take only the data with the smallest Euclidean distance to the target.
deftopN(expected, data, N):
norms = list(map(
lambda row, number:
(np.linalg.norm(row - expected), number),
data,
range(len(data)))) # пары (расстояние, индекс)
norms.sort(key=lambda r: r[0]) # рейтингreturn set(map(lambda r: r[1], norms[:N])) # множество индексовAll is ready. It remains only to peek somewhere our own coordinates (now this can be done in any application with maps) and find all the suitable rollers at the
intersection of the sets A and B :
me_geo = np.array([37.676289, 55.772266]) # мои долгота и широта
me_conv = np.array([1.0, 1.0, 1.0]) # всё: Wi-Fi, туалет, бесплатно
depth = 1
A, B = set(), set() # пока в пересечении ничего нет — расширяем поискwhilenot A & B:
A = topN(me_geo, latlon, depth)
B = topN(me_conv, convenience, depth)
depth += 1for rink in A & B:
print(rinks[rink]["Address"])
For the data from the example, among the 30 nearest skating rinks we get one skating rink on the Old Basmannaya, but with all the conveniences. And you can even walk.

Try using the Moscow open data portal to independently find the open Wi-Fi closest to you, a summer cinema or courtyard surveillance cameras.
