Useless deferred non-blocking messaging in MPI: light analytics and tutorial for those who are a little "in the subject"
Most recently, I had to solve another trivial learning task from my teacher. However, solving it, I managed to pay attention to things about which I had not thought about at all, maybe you did not even think about it. This article is more likely to be useful to students and to all who begin their journey into the world of parallel programming using MPI.

So, the essence of ours, in the essence of the computational problem, is to compare how many times a program using non-blocking delayed point-to-point transmissions is faster than one that uses blocking point-to-point transmissions. We will carry out measurements for input arrays with dimensions of 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 elements. By default, it is proposed to solve it by four processes. And here, actually, and that we will consider:
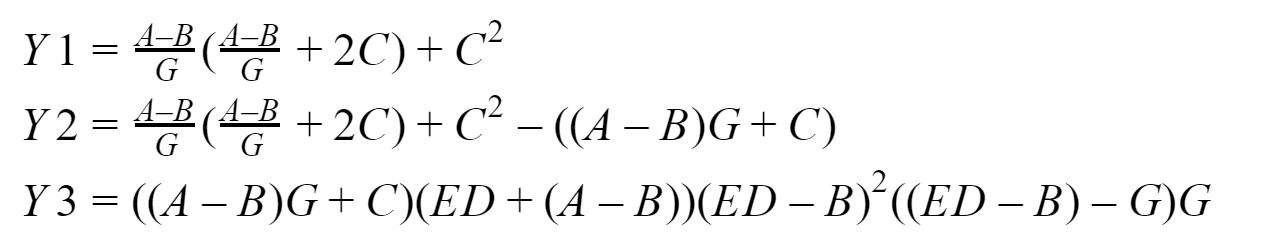
At the output we should have three vectors: Y1, Y2 and Y3, which the zero process will collect. I will test the whole thing on my system based on an Intel processor with 16 GB of RAM. To develop programs, we will use the implementation of the MPI standard from Microsoft version 9.0.1 (at the time of this writing, it is relevant), Visual Studio Community 2017 and not Fortran.
I would not like to describe in detail how the functions of MPI work, which will be used, you can always follow it and look into the documentation , so I will only give a brief overview of what we will use.
For blocking point-to-point messaging, we will use the functions:
MPI_Send - performs blocking message sending, i.e. after calling the function, the process is blocked until the data sent to it is written from its memory into the internal buffer of the MPI environment, after the process continues to work further;
MPI_Recv - performs blocking message reception, i.e. after calling a function, the process is blocked until data from the sending process is received and until this data is completely written to the buffer of the receiving process by the MPI environment.
For deferred non-blocking point-to-point messaging, we will use the functions:
MPI_Send_init — in the background, prepares the medium for sending data that will occur in some future and no locks;
MPI_Recv_init - this function works similarly to the previous one, only this time to receive data;
MPI_Start - starts the process of receiving or sending a message, it also runs in the background ak.a. without blocking;
MPI_Wait- used to check and, if necessary, wait for the completion of the parcel or receive a message, and here it just blocks the process if necessary (if the data is “underreported” or “not received”). For example, a process wants to use data that has not reached it yet - not well, therefore we insert MPI_Wait before the place where it will need this data (we insert it even if there is just a risk of data corruption). Another example, the process started the background data transfer, and after starting the data transfer it immediately began to somehow change the data - not good, so we insert MPI_Wait before the place in the program where it starts to change this data (we also insert it here even if there is just the risk of data corruption).
Thus semantically The sequence of calls for deferred non-blocking exchange is as follows:
I also used MPI_Startall , MPI_Waitall in my test programs , their meaning is basically the same as MPI_Start and MPI_Wait, respectively, only they operate with several packages and / or transmissions. But this is far from the entire list of start and wait functions, there are several more functions for checking the completeness of operations.
For clarity, we construct a graph for performing calculations using four processes. At the same time, it is necessary to try to distribute all vector arithmetic operations relatively evenly among the processes. Here's what I got:
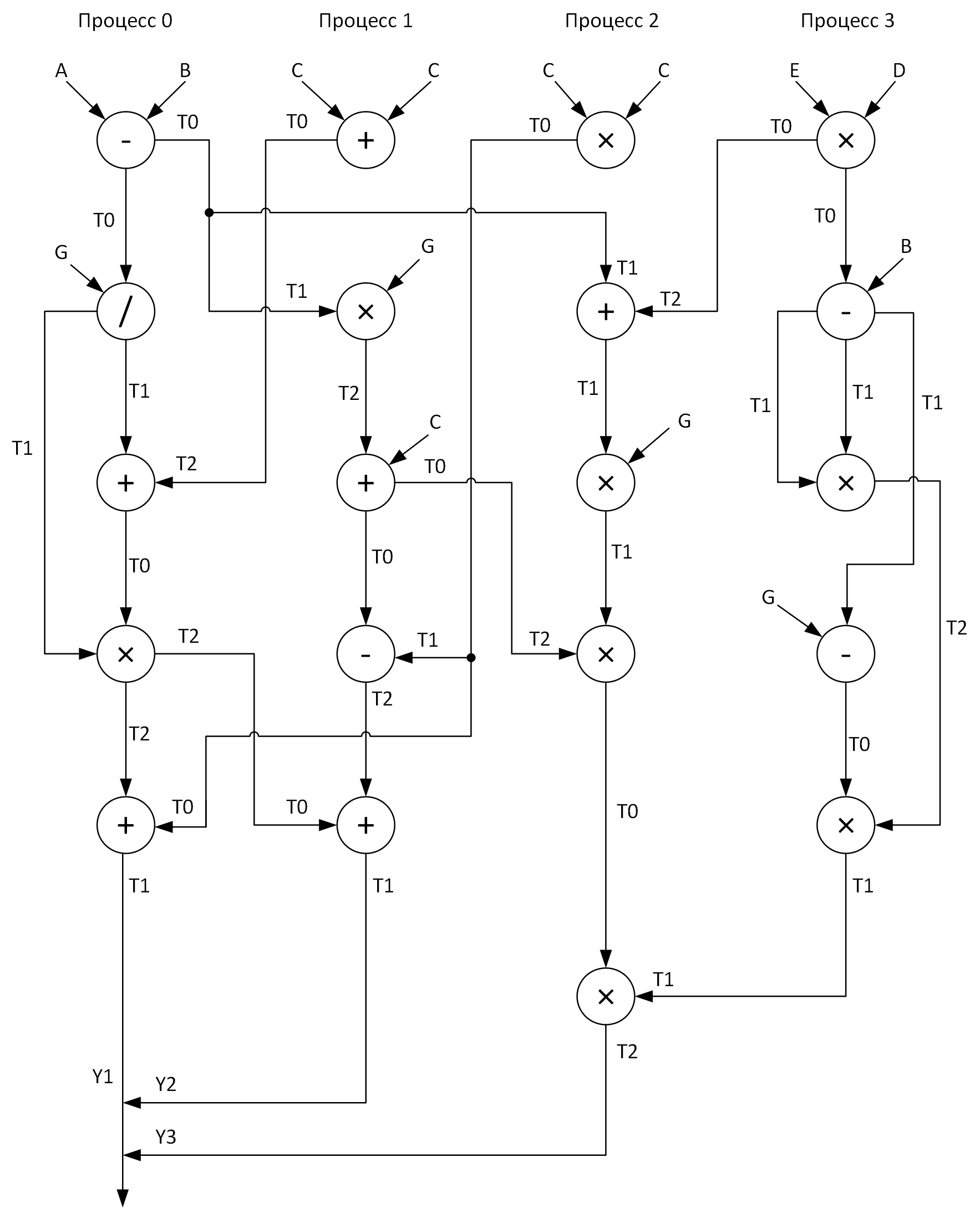
See these T0-T2 arrays? These are buffers for storing intermediate results of operations. Also on the graph in the transmission of messages from one process to another at the beginning of the arrow is the name of the array, whose data is transmitted, and at the end of the arrow - the array that receives this data.
Well, when we finally answered the questions:
It remains only to solve it ...
Next, I will present the codes of the two programs that were discussed above, but first I will give a little more explanation of what and how.
I carried out all vector arithmetic operations in separate procedures (add, sub, mul, div) in order to increase the readability of the code. All input arrays are initialized in accordance with the formulas that I have indicated almost randomly. Since the zero process assembles the results of work from all other processes, therefore, it works the longest, so it is logical to consider its work time equal to the program execution time (as we remember, we are interested in: arithmetic + messaging) in both the first and second cases. We will measure the time intervals using the MPI_Wtime function and at the same time I decided to deduce what resolution I had there withMPI_Wtick (somewhere in the shower, I hope that they will tie up to my invariant TSC, in this case, I am even ready to forgive them for the error associated with the call time of the MPI_Wtime function). So, let's put together everything about which I wrote above and, in accordance with the graph, we will finally develop these programs (and of course we will debug too).
Who is interested to see the code:
Let's run our programs for arrays of different sizes and see what happens. Test results are tabulated in the last column which calculate and write acceleration factor which is defined as follows: By the Start = T exc. non-block. / T block
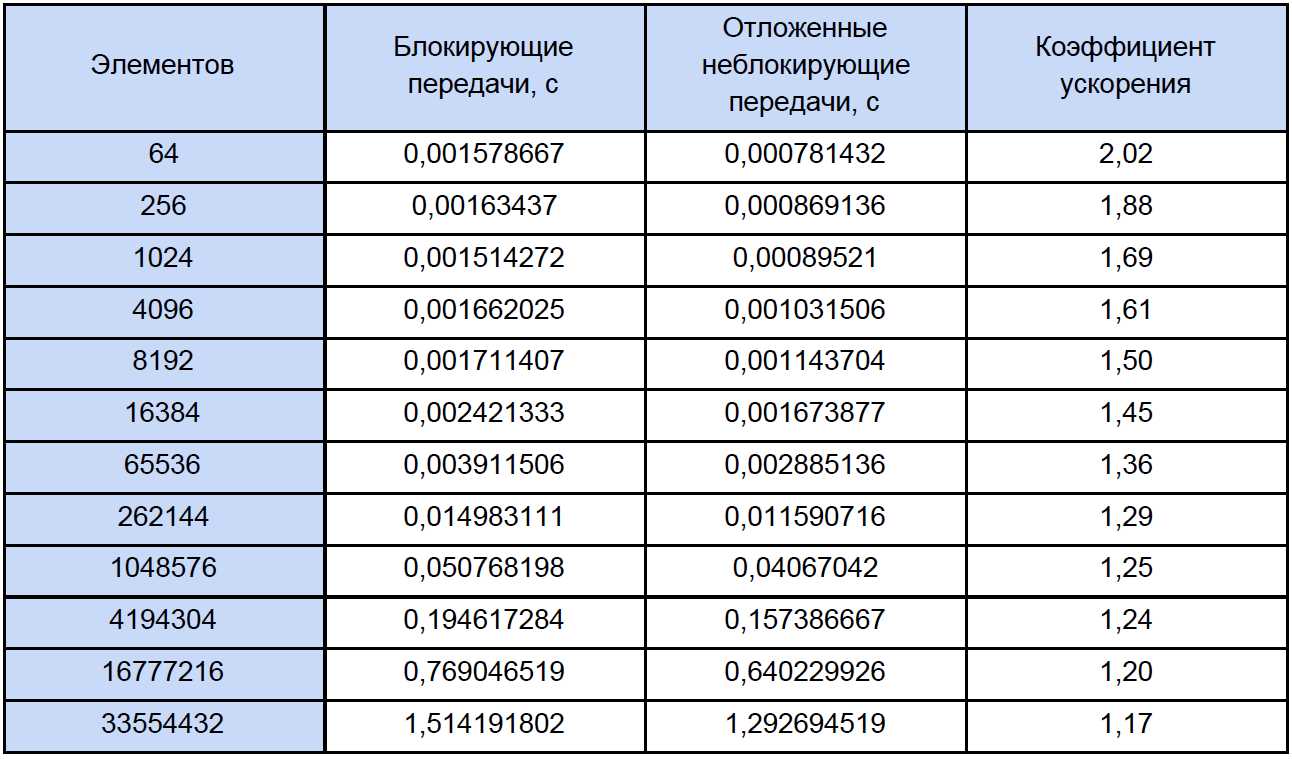
If you look at this table a little more attentively than usual, then you will notice that with an increase in the number of elements being processed, the acceleration factor decreases somehow like this:

Let's try to determine what is the matter? To do this, I propose to write a small test program that will measure the time of each vector arithmetic operation and carefully reduce the results into an ordinary text file.
Here, in fact, the program itself:
At startup, she asks for the number of measurement cycles to enter, I tested for 10,000 cycles. At the output we get the average result for each operation:
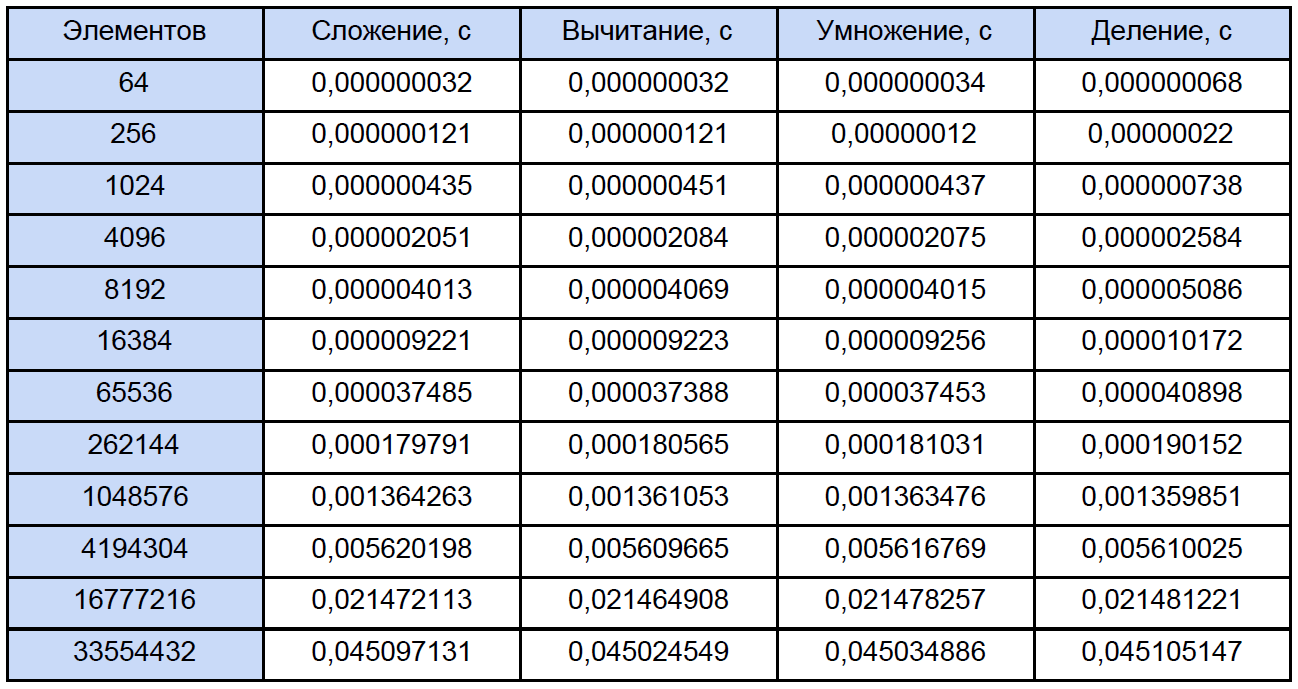
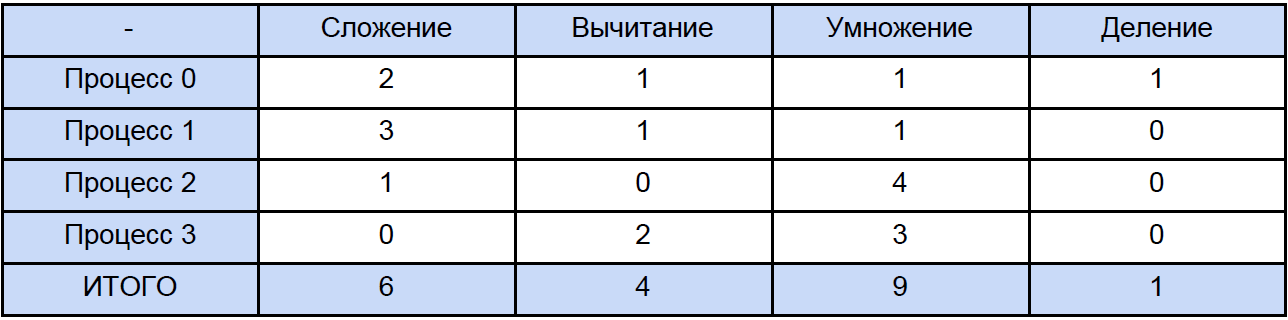
To measure the time I used a high-level QueryPerformanceCounter . I strongly recommend reading this FAQso that most questions on the measurement of time by this function disappear by themselves. According to my observations, it clings to TSC (but theoretically it may not be for it), but returns, according to the certificate, the current number of ticks of the counter. But the fact is that my counter physically cannot measure the time interval of 32 ns (see the first row of the results table). This result is due to the fact that between two calls to the QueryPerformanceCounter, 0 ticks pass, then 1. For the first row in the table, we can only conclude that about a third of the 10,000 results equals 1 tick. So the data in this table for 64, 256 and even for 1024 elements is something quite approximate.Now, let's open any of the programs and calculate how many total operations of each type it meets, traditionally “spreading” the next table:
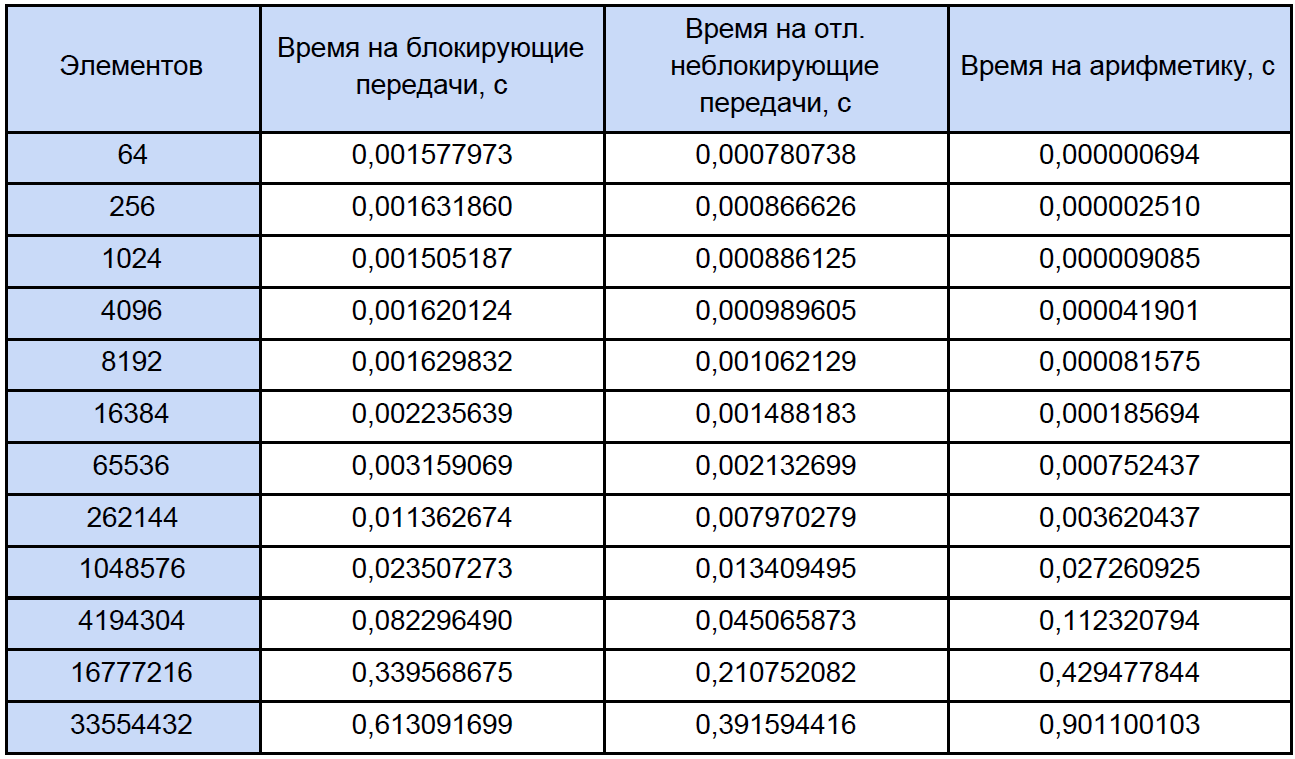
Finally, we know the time of each vector arithmetic operation and how much in our program, try to find out how much time is spent on these operations are in parallel programs and how much time is spent on the blocking and pending non-blocking data exchange between processes and again, for clarity, we put it into the table:
Based on the results of the data, we plot three functions: the first describes the change in time spent on blocking transfers between processes, on the number of array elements, the second on changing the time spent on deferred non-blocking transfers between processes on the number of array elements and the third one on changing time spending on arithmetic operations, from the number of elements of arrays:
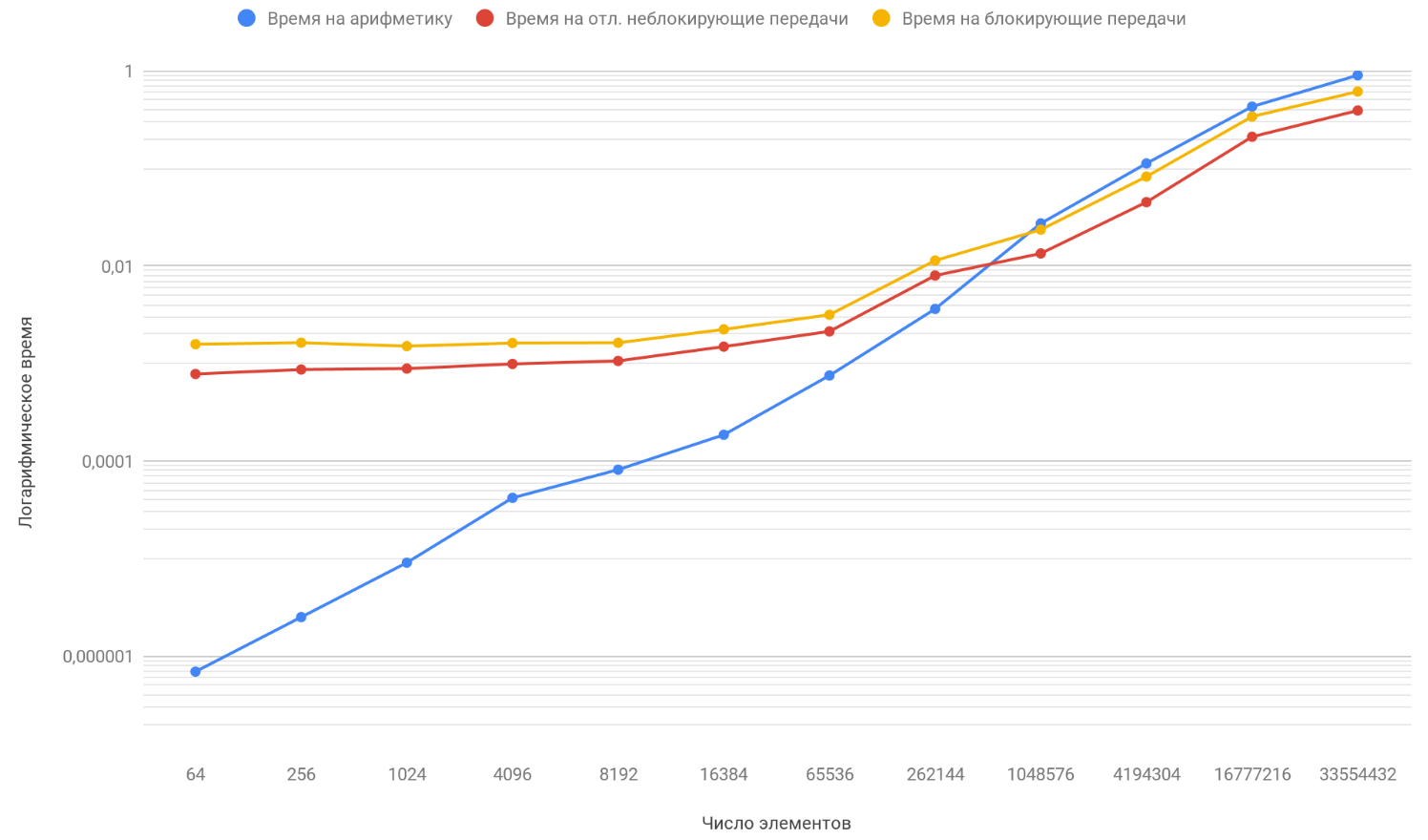
As you have already noticed, the vertical scale of the graph is logarithmic, it is a necessary measure, since the scatter of times is too large and on a regular chart you would not see anything at all. Pay attention to the function of the dependence of the time spent on arithmetic on the number of elements, it successfully overtakes the other two functions by about 1 million elements. The thing is that it grows at infinity faster than its two opponents. Therefore, with an increase in the number of processed elements, the running time of programs is increasingly determined by arithmetic, and not by transmissions. Suppose that you have increased the number of transfers between processes, conceptually you will see that the moment when the arithmetic function will overtake the other two will happen later.
Thus, continuing to increase the length of the arrays, you will come to the conclusion that a program with deferred non-blocking transfers will be only quite a bit faster than the one that uses blocking exchange. And if you rush the length of the arrays to infinity (well, or just take too long arrays), then the time of your program will be 100% read by calculations, and the acceleration factor will safely strive for 1.

Our "Given:"
So, the essence of ours, in the essence of the computational problem, is to compare how many times a program using non-blocking delayed point-to-point transmissions is faster than one that uses blocking point-to-point transmissions. We will carry out measurements for input arrays with dimensions of 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 elements. By default, it is proposed to solve it by four processes. And here, actually, and that we will consider:
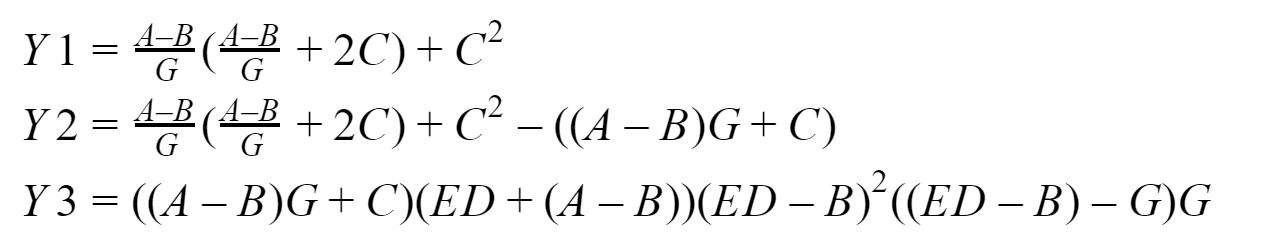
At the output we should have three vectors: Y1, Y2 and Y3, which the zero process will collect. I will test the whole thing on my system based on an Intel processor with 16 GB of RAM. To develop programs, we will use the implementation of the MPI standard from Microsoft version 9.0.1 (at the time of this writing, it is relevant), Visual Studio Community 2017 and not Fortran.
Materiel
I would not like to describe in detail how the functions of MPI work, which will be used, you can always follow it and look into the documentation , so I will only give a brief overview of what we will use.
Blocking exchange
For blocking point-to-point messaging, we will use the functions:
MPI_Send - performs blocking message sending, i.e. after calling the function, the process is blocked until the data sent to it is written from its memory into the internal buffer of the MPI environment, after the process continues to work further;
MPI_Recv - performs blocking message reception, i.e. after calling a function, the process is blocked until data from the sending process is received and until this data is completely written to the buffer of the receiving process by the MPI environment.
Deferred non-blocking exchange
For deferred non-blocking point-to-point messaging, we will use the functions:
MPI_Send_init — in the background, prepares the medium for sending data that will occur in some future and no locks;
MPI_Recv_init - this function works similarly to the previous one, only this time to receive data;
MPI_Start - starts the process of receiving or sending a message, it also runs in the background ak.a. without blocking;
MPI_Wait- used to check and, if necessary, wait for the completion of the parcel or receive a message, and here it just blocks the process if necessary (if the data is “underreported” or “not received”). For example, a process wants to use data that has not reached it yet - not well, therefore we insert MPI_Wait before the place where it will need this data (we insert it even if there is just a risk of data corruption). Another example, the process started the background data transfer, and after starting the data transfer it immediately began to somehow change the data - not good, so we insert MPI_Wait before the place in the program where it starts to change this data (we also insert it here even if there is just the risk of data corruption).
Thus semantically The sequence of calls for deferred non-blocking exchange is as follows:
- MPI_Send_init / MPI_Recv_init - prepare the environment for reception or transmission
- MPI_Start - start the transmit / receive process
- MPI_Wait - we call if there is a risk of damage (including “underrepairing” and “underpatching”) of transmitted or received data
I also used MPI_Startall , MPI_Waitall in my test programs , their meaning is basically the same as MPI_Start and MPI_Wait, respectively, only they operate with several packages and / or transmissions. But this is far from the entire list of start and wait functions, there are several more functions for checking the completeness of operations.
Process Relationship Architecture
For clarity, we construct a graph for performing calculations using four processes. At the same time, it is necessary to try to distribute all vector arithmetic operations relatively evenly among the processes. Here's what I got:

See these T0-T2 arrays? These are buffers for storing intermediate results of operations. Also on the graph in the transmission of messages from one process to another at the beginning of the arrow is the name of the array, whose data is transmitted, and at the end of the arrow - the array that receives this data.
Well, when we finally answered the questions:
- What kind of problem we solve?
- What tools will we use to solve it?
- How will we solve it?
It remains only to solve it ...
Our "Solution:"
Next, I will present the codes of the two programs that were discussed above, but first I will give a little more explanation of what and how.
I carried out all vector arithmetic operations in separate procedures (add, sub, mul, div) in order to increase the readability of the code. All input arrays are initialized in accordance with the formulas that I have indicated almost randomly. Since the zero process assembles the results of work from all other processes, therefore, it works the longest, so it is logical to consider its work time equal to the program execution time (as we remember, we are interested in: arithmetic + messaging) in both the first and second cases. We will measure the time intervals using the MPI_Wtime function and at the same time I decided to deduce what resolution I had there withMPI_Wtick (somewhere in the shower, I hope that they will tie up to my invariant TSC, in this case, I am even ready to forgive them for the error associated with the call time of the MPI_Wtime function). So, let's put together everything about which I wrote above and, in accordance with the graph, we will finally develop these programs (and of course we will debug too).
Who is interested to see the code:
Program with blocking data transfers
#include"pch.h"#include<iostream>#include<iomanip>#include<fstream>#include<mpi.h>usingnamespacestd;
voidadd(double *A, double *B, double *C, int n);
voidsub(double *A, double *B, double *C, int n);
voidmul(double *A, double *B, double *C, int n);
voiddiv(double *A, double *B, double *C, int n);
intmain(int argc, char **argv){
if (argc < 2)
{
return1;
}
int n = atoi(argv[1]);
int rank;
double start_time, end_time;
MPI_Status status;
double *A = newdouble[n];
double *B = newdouble[n];
double *C = newdouble[n];
double *D = newdouble[n];
double *E = newdouble[n];
double *G = newdouble[n];
double *T0 = newdouble[n];
double *T1 = newdouble[n];
double *T2 = newdouble[n];
for (int i = 0; i < n; i++)
{
A[i] = double (2 * i + 1);
B[i] = double(2 * i);
C[i] = double(0.003 * (i + 1));
D[i] = A[i] * 0.001;
E[i] = B[i];
G[i] = C[i];
}
cout.setf(ios::fixed);
cout << fixed << setprecision(9);
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
if (rank == 0)
{
start_time = MPI_Wtime();
sub(A, B, T0, n);
MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD);
MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD);
div(T0, G, T1, n);
MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status);
add(T1, T2, T0, n);
mul(T0, T1, T2, n);
MPI_Recv(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status);
MPI_Send(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD);
add(T0, T2, T1, n);
MPI_Recv(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status);
MPI_Recv(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status);
end_time = MPI_Wtime();
cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl;
cout << "Thread " << rank << " execution time: " << end_time - start_time << endl;
}
if (rank == 1)
{
add(C, C, T0, n);
MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status);
MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
mul(T1, G, T2, n);
add(T2, C, T0, n);
MPI_Recv(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status);
MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD);
sub(T1, T0, T2, n);
MPI_Recv(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status);
add(T0, T2, T1, n);
MPI_Send(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
}
if (rank == 2)
{
mul(C, C, T0, n);
MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status);
MPI_Recv(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status);
MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD);
MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
add(T1, T2, T0, n);
mul(T0, G, T1, n);
MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status);
mul(T1, T2, T0, n);
MPI_Recv(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status);
mul(T0, T1, T2, n);
MPI_Send(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
}
if (rank == 3)
{
mul(E, D, T0, n);
MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD);
sub(T0, B, T1, n);
mul(T1, T1, T2, n);
sub(T1, G, T0, n);
mul(T0, T2, T1, n);
MPI_Send(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD);
}
MPI_Finalize();
delete[] A;
delete[] B;
delete[] C;
delete[] D;
delete[] E;
delete[] G;
delete[] T0;
delete[] T1;
delete[] T2;
return0;
}
voidadd(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] + B[i];
}
}
voidsub(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] - B[i];
}
}
voidmul(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] * B[i];
}
}
voiddiv(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] / B[i];
}
}
Program with deferred non-blocking data transfers
#include"pch.h"#include<iostream>#include<iomanip>#include<fstream>#include<mpi.h>usingnamespacestd;
voidadd(double *A, double *B, double *C, int n);
voidsub(double *A, double *B, double *C, int n);
voidmul(double *A, double *B, double *C, int n);
voiddiv(double *A, double *B, double *C, int n);
intmain(int argc, char **argv){
if (argc < 2)
{
return1;
}
int n = atoi(argv[1]);
int rank;
double start_time, end_time;
MPI_Request request[7];
MPI_Status statuses[4];
double *A = newdouble[n];
double *B = newdouble[n];
double *C = newdouble[n];
double *D = newdouble[n];
double *E = newdouble[n];
double *G = newdouble[n];
double *T0 = newdouble[n];
double *T1 = newdouble[n];
double *T2 = newdouble[n];
for (int i = 0; i < n; i++)
{
A[i] = double(2 * i + 1);
B[i] = double(2 * i);
C[i] = double(0.003 * (i + 1));
D[i] = A[i] * 0.001;
E[i] = B[i];
G[i] = C[i];
}
cout.setf(ios::fixed);
cout << fixed << setprecision(9);
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
if (rank == 0)
{
start_time = MPI_Wtime();
MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[0]);//
MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]);//
MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);//
MPI_Recv_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);//
MPI_Send_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);//
MPI_Recv_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[5]);//
MPI_Recv_init(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[6]);//
MPI_Start(&request[2]);
sub(A, B, T0, n);
MPI_Startall(2, &request[0]);
div(T0, G, T1, n);
MPI_Waitall(3, &request[0], statuses);
add(T1, T2, T0, n);
mul(T0, T1, T2, n);
MPI_Startall(2, &request[3]);
MPI_Wait(&request[3], &statuses[0]);
add(T0, T2, T1, n);
MPI_Startall(2, &request[5]);
MPI_Wait(&request[4], &statuses[0]);
MPI_Waitall(2, &request[5], statuses);
end_time = MPI_Wtime();
cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl;
cout << "Thread " << rank << " execution time: " << end_time - start_time << endl;
}
if (rank == 1)
{
MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);//
MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[1]);//
MPI_Recv_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[2]);//
MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);//
MPI_Recv_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[4]);//
MPI_Send_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[5]);//
MPI_Start(&request[0]);
add(C, C, T0, n);
MPI_Start(&request[1]);
MPI_Wait(&request[0], &statuses[0]);
mul(T1, G, T2, n);
MPI_Start(&request[2]);
MPI_Wait(&request[1], &statuses[0]);
add(T2, C, T0, n);
MPI_Start(&request[3]);
MPI_Wait(&request[2], &statuses[0]);
sub(T1, T0, T2, n);
MPI_Wait(&request[3], &statuses[0]);
MPI_Start(&request[4]);
MPI_Wait(&request[4], &statuses[0]);
add(T0, T2, T1, n);
MPI_Start(&request[5]);
MPI_Wait(&request[5], &statuses[0]);
}
if (rank == 2)
{
MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);//
MPI_Recv_init(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[1]);//
MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);//
MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[3]);//
MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);//
MPI_Recv_init(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[5]);//
MPI_Send_init(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[6]);//
MPI_Startall(2, &request[0]);
mul(C, C, T0, n);
MPI_Startall(2, &request[2]);
MPI_Waitall(4, &request[0], statuses);
add(T1, T2, T0, n);
MPI_Start(&request[4]);
mul(T0, G, T1, n);
MPI_Wait(&request[4], &statuses[0]);
mul(T1, T2, T0, n);
MPI_Start(&request[5]);
MPI_Wait(&request[5], &statuses[0]);
mul(T0, T1, T2, n);
MPI_Start(&request[6]);
MPI_Wait(&request[6], &statuses[0]);
}
if (rank == 3)
{
MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[0]);
MPI_Send_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]);
mul(E, D, T0, n);
MPI_Start(&request[0]);
sub(T0, B, T1, n);
mul(T1, T1, T2, n);
MPI_Wait(&request[0], &statuses[0]);
sub(T1, G, T0, n);
mul(T0, T2, T1, n);
MPI_Start(&request[1]);
MPI_Wait(&request[1], &statuses[0]);
}
MPI_Finalize();
delete[] A;
delete[] B;
delete[] C;
delete[] D;
delete[] E;
delete[] G;
delete[] T0;
delete[] T1;
delete[] T2;
return0;
}
voidadd(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] + B[i];
}
}
voidsub(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] - B[i];
}
}
voidmul(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] * B[i];
}
}
voiddiv(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] / B[i];
}
}
Testing and analysis
Let's run our programs for arrays of different sizes and see what happens. Test results are tabulated in the last column which calculate and write acceleration factor which is defined as follows: By the Start = T exc. non-block. / T block

If you look at this table a little more attentively than usual, then you will notice that with an increase in the number of elements being processed, the acceleration factor decreases somehow like this:

Let's try to determine what is the matter? To do this, I propose to write a small test program that will measure the time of each vector arithmetic operation and carefully reduce the results into an ordinary text file.
Here, in fact, the program itself:
Time measurement
#include"pch.h"#include<iostream>#include<iomanip>#include<Windows.h>#include<fstream>usingnamespacestd;
voidadd(double *A, double *B, double *C, int n);
voidsub(double *A, double *B, double *C, int n);
voidmul(double *A, double *B, double *C, int n);
voiddiv(double *A, double *B, double *C, int n);
intmain(){
structres
{double add;
double sub;
double mul;
double div;
};
int i, j, k, n, loop;
LARGE_INTEGER start_time, end_time, freq;
ofstream fout("test_measuring.txt");
int N[12] = { 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 };
SetConsoleOutputCP(1251);
cout << "Введите число циклов loop: ";
cin >> loop;
fout << setiosflags(ios::fixed) << setiosflags(ios::right) << setprecision(9);
fout << "Циклов измерений: " << loop << endl;
fout << setw(10) << "\n Элементов" << setw(30) << "Ср. время суммирования (c)" << setw(30) << "Ср. время вычитания (c)"
<< setw(30) << "Ср.время умножения (c)" << setw(30) << "Ср. время деления (c)" << endl;
QueryPerformanceFrequency(&freq);
cout << "\nЧастота счета: " << freq.QuadPart << " Гц" << endl;
for (k = 0; k < sizeof(N) / sizeof(int); k++)
{
res output = {};
n = N[k];
double *A = newdouble[n];
double *B = newdouble[n];
double *C = newdouble[n];
for (i = 0; i < n; i++)
{
A[i] = 2.0 * i;
B[i] = 2.0 * i + 1;
C[i] = 0;
}
for (j = 0; j < loop; j++)
{
QueryPerformanceCounter(&start_time);
add(A, B, C, n);
QueryPerformanceCounter(&end_time);
output.add += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart);
QueryPerformanceCounter(&start_time);
sub(A, B, C, n);
QueryPerformanceCounter(&end_time);
output.sub += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart);
QueryPerformanceCounter(&start_time);
mul(A, B, C, n);
QueryPerformanceCounter(&end_time);
output.mul += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart);
QueryPerformanceCounter(&start_time);
div(A, B, C, n);
QueryPerformanceCounter(&end_time);
output.div += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart);
}
fout << setw(10) << n << setw(30) << output.add / loop << setw(30) << output.sub / loop
<< setw(30) << output.mul / loop << setw(30) << output.div / loop << endl;
delete[] A;
delete[] B;
delete[] C;
}
fout.close();
cout << endl;
system("pause");
return0;
}
voidadd(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] + B[i];
}
}
voidsub(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] - B[i];
}
}
voidmul(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] * B[i];
}
}
voiddiv(double *A, double *B, double *C, int n){
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] / B[i];
}
}
At startup, she asks for the number of measurement cycles to enter, I tested for 10,000 cycles. At the output we get the average result for each operation:

To measure the time I used a high-level QueryPerformanceCounter . I strongly recommend reading this FAQso that most questions on the measurement of time by this function disappear by themselves. According to my observations, it clings to TSC (but theoretically it may not be for it), but returns, according to the certificate, the current number of ticks of the counter. But the fact is that my counter physically cannot measure the time interval of 32 ns (see the first row of the results table). This result is due to the fact that between two calls to the QueryPerformanceCounter, 0 ticks pass, then 1. For the first row in the table, we can only conclude that about a third of the 10,000 results equals 1 tick. So the data in this table for 64, 256 and even for 1024 elements is something quite approximate.Now, let's open any of the programs and calculate how many total operations of each type it meets, traditionally “spreading” the next table:

Finally, we know the time of each vector arithmetic operation and how much in our program, try to find out how much time is spent on these operations are in parallel programs and how much time is spent on the blocking and pending non-blocking data exchange between processes and again, for clarity, we put it into the table:

Based on the results of the data, we plot three functions: the first describes the change in time spent on blocking transfers between processes, on the number of array elements, the second on changing the time spent on deferred non-blocking transfers between processes on the number of array elements and the third one on changing time spending on arithmetic operations, from the number of elements of arrays:

As you have already noticed, the vertical scale of the graph is logarithmic, it is a necessary measure, since the scatter of times is too large and on a regular chart you would not see anything at all. Pay attention to the function of the dependence of the time spent on arithmetic on the number of elements, it successfully overtakes the other two functions by about 1 million elements. The thing is that it grows at infinity faster than its two opponents. Therefore, with an increase in the number of processed elements, the running time of programs is increasingly determined by arithmetic, and not by transmissions. Suppose that you have increased the number of transfers between processes, conceptually you will see that the moment when the arithmetic function will overtake the other two will happen later.
Results
Thus, continuing to increase the length of the arrays, you will come to the conclusion that a program with deferred non-blocking transfers will be only quite a bit faster than the one that uses blocking exchange. And if you rush the length of the arrays to infinity (well, or just take too long arrays), then the time of your program will be 100% read by calculations, and the acceleration factor will safely strive for 1.
