Writing Real Perlin Noise
By a search query, the noise of perlin immediately comes across this translation on Habré. As rightly noted in the comments to the publication, this is not about Perlin's noise at all. Perhaps the author of the translation himself was not in the know.
What compares the noise of Perlin, you caneasily see if you compare the pictures.
Ordinary noise (from the same article):

Perlin noise:

And by increasing the number of octaves, the first picture cannot be brought closer to the second. I will not describe the advantages of Perlin noise and its scope (because the article is about programming, not about application), but I will try to explain how it is implemented. I think it will be useful to many programmers, because Ken Perlin’s hacker sources do not explain much even if there are comments.
Surprisingly, judging by the reviews in PM and in the commentary, it turned out that not everyone is able to see at all any difference between a simple smoothed noise in grayscale and Perlin's noise. But, probably, because of this paradox, the very article appeared and was popular.
I'll try to give a tip: the
first picture consists of pronounced pixels (enlarged) of different shades of gray: the

second (Perlin noise) looks like black and white blurry worms.
Here's what happens after simple operations in a graphical editor (search for borders, invert, posterization):
Perlin:

Picture from the article (exactly the same operations are applied):

Yes, in fractal noise, if there are a lot of octaves, then it’s really difficult to understand what is in the original - Perlin or not. But this is not a reason to call the fractal noise Perlin Noise.
This will end with a description of the difference.
The end of the retreat.
Let's consider a two-dimensional option. For now, we will write only the blank class. The input is a two-dimensional vector or two floating-point numbers: x, y.
The return value is a number from -1.0 to 1.0:
The idea of normal smoothed noise is that there is a discrete grid of pseudo-random values, and interpolation occurs between the grid nodes for the requested point (the closer the point to any grid node, the more its value corresponds to the node value).
Here, in the third conditional square, the point in the very center after interpolation will have a value of 3:
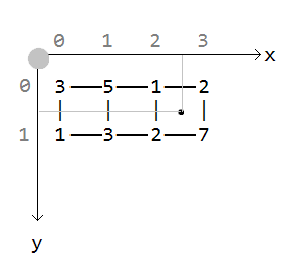
Let us consider in more detail how the triple turns out there. Point coordinates: The integer coordinates of the point (upper left corner of the square): obtained by rounding to the lower side (floor function). The local coordinates of the point inside the square are obtained by subtraction:
We take the value of the upper left corner of the square (1) and the upper right (2). Interpolate the top face using the local x coordinate (0.5). Linear interpolation looks like this:
We take the value of the lower left corner of the square (2) and the lower right (7). Interpolate the bottom face using the same local coordinate x (0.5).
Results: Now the upper and lower interpolation remains using the local y coordinate (also 0.5): Bilinear interpolation is the simplest but the result is not the most attractive. Other interpolation options involve modifying the local coordinate (parameter t) before interpolation. Smoother transitions are obtained near the boundary values (0 and 1). In the noise of Perlin, the first option is involved, it gives a fairly strong curvature.

Everything is very simple:
1. At the grid nodes - pseudo-random vectors (two-dimensional for two-dimensional noise, three-dimensional for three-dimensional, and so on), and not pseudo-random numbers .
2. We interpolate between the scalar products of a) vectors from the vertices of the square to the point inside the square (the cube in the three-dimensional version) and b) pseudorandom vectors (when describing Perlin noise they are called gradient vectors).
In his improved version of noise, Ken Perlin uses only 12 gradient vectors. For the two-dimensional version, only 4 are required - by the number of faces (the square has 4). The vectors are directed (conditionally from the center of the cube / square) towards each of the faces and are not normalized.
Here they are:

So, each node of the grid corresponds to one of four vectors. Let the vector be an array of floats.
We need a scalar product of vectors:
The main method:
As a bonus:
And the last one is using a table with random numbers. In Ken Perlin's code, such a table is written manually and the values get from there in a completely different way. Here you can experiment and the noise uniformity and the absence of explicit patterns in it depend a lot on this.
I did
Result:

What compares the noise of Perlin, you can
Ordinary noise (from the same article):

Perlin noise:

And by increasing the number of octaves, the first picture cannot be brought closer to the second. I will not describe the advantages of Perlin noise and its scope (because the article is about programming, not about application), but I will try to explain how it is implemented. I think it will be useful to many programmers, because Ken Perlin’s hacker sources do not explain much even if there are comments.
Retreat
Surprisingly, judging by the reviews in PM and in the commentary, it turned out that not everyone is able to see at all any difference between a simple smoothed noise in grayscale and Perlin's noise. But, probably, because of this paradox, the very article appeared and was popular.
I'll try to give a tip: the
first picture consists of pronounced pixels (enlarged) of different shades of gray: the

second (Perlin noise) looks like black and white blurry worms.
Here's what happens after simple operations in a graphical editor (search for borders, invert, posterization):
Perlin:

Picture from the article (exactly the same operations are applied):

Yes, in fractal noise, if there are a lot of octaves, then it’s really difficult to understand what is in the original - Perlin or not. But this is not a reason to call the fractal noise Perlin Noise.
This will end with a description of the difference.
The end of the retreat.
Let's consider a two-dimensional option. For now, we will write only the blank class. The input is a two-dimensional vector or two floating-point numbers: x, y.
The return value is a number from -1.0 to 1.0:
public class Perlin2d
{
public float Noise(float x, float y)
{
throw new NotImplementedException();
}
}
A few words about interpolation
The idea of normal smoothed noise is that there is a discrete grid of pseudo-random values, and interpolation occurs between the grid nodes for the requested point (the closer the point to any grid node, the more its value corresponds to the node value).
Here, in the third conditional square, the point in the very center after interpolation will have a value of 3:

Let us consider in more detail how the triple turns out there. Point coordinates: The integer coordinates of the point (upper left corner of the square): obtained by rounding to the lower side (floor function). The local coordinates of the point inside the square are obtained by subtraction:
x:2.5,
y:0.5
x:2,
y:0
x = 2.5 – 2 = 0.5,
y = 0.5 – 0 = 0.5
We take the value of the upper left corner of the square (1) and the upper right (2). Interpolate the top face using the local x coordinate (0.5). Linear interpolation looks like this:
static float Lerp(float a, float b, float t)
{
// return a * (t - 1) + b * t; можно переписать с одним умножением (раскрыть скобки, взять в другие скобки):
return a + (b - a) * t;
}
We take the value of the lower left corner of the square (2) and the lower right (7). Interpolate the bottom face using the same local coordinate x (0.5).
Results: Now the upper and lower interpolation remains using the local y coordinate (also 0.5): Bilinear interpolation is the simplest but the result is not the most attractive. Other interpolation options involve modifying the local coordinate (parameter t) before interpolation. Smoother transitions are obtained near the boundary values (0 and 1). In the noise of Perlin, the first option is involved, it gives a fairly strong curvature.
верхняя: 1.5
нижняя: 4.5
1.5 * 0.5 + 4.5 * (1 – 0.5) = 3

static float QunticCurve(float t)
{
return t * t * t * (t * (t * 6 - 15) + 10);
}
...
// комбинирование с функцией линейной интерполяции:
Lerp(a, b, QuinticCurve(t))
The main idea and difference of Perlin noise
Everything is very simple:
1. At the grid nodes - pseudo-random vectors (two-dimensional for two-dimensional noise, three-dimensional for three-dimensional, and so on), and not pseudo-random numbers .
2. We interpolate between the scalar products of a) vectors from the vertices of the square to the point inside the square (the cube in the three-dimensional version) and b) pseudorandom vectors (when describing Perlin noise they are called gradient vectors).
In his improved version of noise, Ken Perlin uses only 12 gradient vectors. For the two-dimensional version, only 4 are required - by the number of faces (the square has 4). The vectors are directed (conditionally from the center of the cube / square) towards each of the faces and are not normalized.
Here they are:
{ 1, 0 }
{ -1, 0 }
{ 0, 1 }
{ 0,-1 }

So, each node of the grid corresponds to one of four vectors. Let the vector be an array of floats.
float[] GetPseudoRandomGradientVector(int x, int y)
{
int v = // псевдо-случайное число от 0 до 3 которое всегда неизменно при данных x и y
switch (v)
{
case 0: return new float[]{ 1, 0 };
case 1: return new float[]{ -1, 0 };
case 2: return new float[]{ 0, 1 };
default: return new float[]{ 0,-1 };
}
}
Implementation
We need a scalar product of vectors:
static float Dot(float[] a, float[] b)
{
return a[0] * b[0] + a[1] * b[1];
}
The main method:
public float Noise(float fx, float fy)
{
// сразу находим координаты левой верхней вершины квадрата
int left = (int)System.Math.Floor(fx);
int top = (int)System.Math.Floor(fy);
// а теперь локальные координаты точки внутри квадрата
float pointInQuadX = fx - left;
float pointInQuadY = fy - top;
// извлекаем градиентные векторы для всех вершин квадрата:
float[] topLeftGradient = GetPseudoRandomGradientVector(left, top );
float[] topRightGradient = GetPseudoRandomGradientVector(left+1, top );
float[] bottomLeftGradient = GetPseudoRandomGradientVector(left, top+1);
float[] bottomRightGradient = GetPseudoRandomGradientVector(left+1, top+1);
// вектора от вершин квадрата до точки внутри квадрата:
float[] distanceToTopLeft = new float[]{ pointInQuadX, pointInQuadY };
float[] distanceToTopRight = new float[]{ pointInQuadX-1, pointInQuadY };
float[] distanceToBottomLeft = new float[]{ pointInQuadX, pointInQuadY-1 };
float[] distanceToBottomRight = new float[]{ pointInQuadX-1, pointInQuadY-1 };
// считаем скалярные произведения между которыми будем интерполировать
/*
tx1--tx2
| |
bx1--bx2
*/
float tx1 = Dot(distanceToTopLeft, topLeftGradient);
float tx2 = Dot(distanceToTopRight, topRightGradient);
float bx1 = Dot(distanceToBottomLeft, bottomLeftGradient);
float bx2 = Dot(distanceToBottomRight, bottomRightGradient);
// готовим параметры интерполяции, чтобы она не была линейной:
pointInQuadX = QunticCurve(pointInQuadX);
pointInQuadY = QunticCurve(pointInQuadY);
// собственно, интерполяция:
float tx = Lerp(tx1, tx2, pointInQuadX);
float bx = Lerp(bx1, bx2, pointInQuadX);
float tb = Lerp(tx, bx, pointInQuadY);
// возвращаем результат:
return tb;
}
As a bonus:
multi-octave noise
public float Noise(float fx, float fy, int octaves, float persistence = 0.5f)
{
float amplitude = 1; // сила применения шума к общей картине, будет уменьшаться с "мельчанием" шума
// как сильно уменьшаться - регулирует persistence
float max = 0; // необходимо для нормализации результата
float result = 0; // накопитель результата
while (octaves-- > 0)
{
max += amplitude;
result += Noise(fx, fy) * amplitude;
amplitude *= persistence;
fx *= 2; // удваиваем частоту шума (делаем его более мелким) с каждой октавой
fy *= 2;
}
return result/max;
}
And the last one is using a table with random numbers. In Ken Perlin's code, such a table is written manually and the values get from there in a completely different way. Here you can experiment and the noise uniformity and the absence of explicit patterns in it depend a lot on this.
I did
So
& 3 truncates any int32 number to 3, read about the AND operation on Wikipedia An
operation like % 3 would also work, but much more slowly.
class Perlin2D
{
byte[] permutationTable;
public Perlin2D(int seed = 0)
{
var rand = new System.Random(seed);
permutationTable = new byte[1024];
rand.NextBytes(permutationTable); // заполняем случайными байтами
}
private float[] GetPseudoRandomGradientVector(int x, int y)
{
// хэш-функция с Простыми числами, обрезкой результата до размера массива со случайными байтами
int v = (int)(((x * 1836311903) ^ (y * 2971215073) + 4807526976) & 1023);
v = permutationTable[v]&3;
switch (v)
{
...
& 3 truncates any int32 number to 3, read about the AND operation on Wikipedia An
operation like % 3 would also work, but much more slowly.
Entire source code (no comment)
class Perlin2D
{
byte[] permutationTable;
public Perlin2D(int seed = 0)
{
var rand = new System.Random(seed);
permutationTable = new byte[1024];
rand.NextBytes(permutationTable);
}
private float[] GetPseudoRandomGradientVector(int x, int y)
{
int v = (int)(((x * 1836311903) ^ (y * 2971215073) + 4807526976) & 1023);
v = permutationTable[v]&3;
switch (v)
{
case 0: return new float[]{ 1, 0 };
case 1: return new float[]{ -1, 0 };
case 2: return new float[]{ 0, 1 };
default: return new float[]{ 0,-1 };
}
}
static float QunticCurve(float t)
{
return t * t * t * (t * (t * 6 - 15) + 10);
}
static float Lerp(float a, float b, float t)
{
return a + (b - a) * t;
}
static float Dot(float[] a, float[] b)
{
return a[0] * b[0] + a[1] * b[1];
}
public float Noise(float fx, float fy)
{
int left = (int)System.Math.Floor(fx);
int top = (int)System.Math.Floor(fy);
float pointInQuadX = fx - left;
float pointInQuadY = fy - top;
float[] topLeftGradient = GetPseudoRandomGradientVector(left, top );
float[] topRightGradient = GetPseudoRandomGradientVector(left+1, top );
float[] bottomLeftGradient = GetPseudoRandomGradientVector(left, top+1);
float[] bottomRightGradient = GetPseudoRandomGradientVector(left+1, top+1);
float[] distanceToTopLeft = new float[]{ pointInQuadX, pointInQuadY };
float[] distanceToTopRight = new float[]{ pointInQuadX-1, pointInQuadY };
float[] distanceToBottomLeft = new float[]{ pointInQuadX, pointInQuadY-1 };
float[] distanceToBottomRight = new float[]{ pointInQuadX-1, pointInQuadY-1 };
float tx1 = Dot(distanceToTopLeft, topLeftGradient);
float tx2 = Dot(distanceToTopRight, topRightGradient);
float bx1 = Dot(distanceToBottomLeft, bottomLeftGradient);
float bx2 = Dot(distanceToBottomRight, bottomRightGradient);
pointInQuadX = QunticCurve(pointInQuadX);
pointInQuadY = QunticCurve(pointInQuadY);
float tx = Lerp(tx1, tx2, pointInQuadX);
float bx = Lerp(bx1, bx2, pointInQuadX);
float tb = Lerp(tx, bx, pointInQuadY);
return tb;
}
public float Noise(float fx, float fy, int octaves, float persistence = 0.5f)
{
float amplitude = 1;
float max = 0;
float result = 0;
while (octaves-- > 0)
{
max += amplitude;
result += Noise(fx, fy) * amplitude;
amplitude *= persistence;
fx *= 2;
fy *= 2;
}
return result/max;
}
}
Result:

