Numerical test of abc hypothesis (yes, the one)
Hi, Habr.
OnGeektimes Habr there were already several articles about the abc-hypothesis (for example, in 2013 and in 2018 ). The story itself about the theorem, which for many years cannot be proved for many years, and then cannot be checked for as many years, certainly deserves at least a feature film. But in the shadow of this wonderful story, the theorem itself is considered too superficially, although it is no less interesting. Even by the fact that the abc hypothesis is one of the few unsolved problems of modern science, the task of which can be understood even by a fifth-grader. If this hypothesis is indeed true, then the proof of other important theorems easily follows from it, for example, the proof of Fermat's theorem .
Without claiming Mochizuki’s laurels, Ialso decided to try and decided to check with the computer how much the equality promised in the hypothesis was fulfilled. Actually, why not - modern processors are not only to play games - why not use a computer in its main (compute - compute) purpose ...
Who cares what happened, I ask for cat.
Start over. What is the theorem about? As Wikipedia says (the wording in the English version is a little more understandable), for mutually simple (without common divisors) numbers a, b and c, such that a + b = c, for any ε> 0 there is a limited number of triples a + b = c, such that:
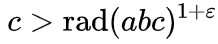
The function rad is called the radical , and denotes the product of prime factors of a number. For example, rad (16) = rad (2 * 2 * 2 * 2) = 2, rad (17) = 17 (17 is a prime number), rad (18) = rad (2 * 3 * 3) = 2 * 3 = 6, rad (1,000,000) = rad (2 ^ 6 ⋅ 5 ^ 6) = 2 * 5 = 10.
Actually, the essence of the theorem is that the number of such triples is quite small. For example, if we take at random ε = 0.2 and equality 100 + 27 = 127: rad (100) = rad (2 * 2 * 5 * 5) = 10, rad (27) = rad (3 * 3 * 3) = 3, rad (127) = 127, rad (a * b * c) = rad (a) * rad (b) * rad (s) = 3810, 3810 ^ 1.2 is clearly greater than 127, the inequality is not satisfied. But there are exceptions, for example, for equality 49 + 576 = 625, the condition of the theorem is fulfilled (those who wish can check it themselves).
The next key moment for us is of these equalities, according to the theorem, a limited number. Those. This means that you can just try them all on your computer. In the end, this gives us theNobel Prize is quite an interesting programming problem.
So let's get started.
The first version was written in Python, and although this language is too slow for such calculations, writing code on it is easy and simple, which is convenient for prototyping.
Getting the radical : decompose the number into prime factors, then remove the repetitions, converting the array into a set. Then we just get the product of all the elements.
Mutually simple numbers : decompose numbers into factors, and just check the intersection of sets.
Check : we use already created functions, everything is simple.
Those interested can experiment on their own by copying the above code into any online Python editor. Of course, the code works as expectedly slowly, and going through all the triples to at least a million would be too long. Below is a optimized version under the spoiler, it is recommended to use it.
The final version was rewritten in C ++ using multithreading and some optimization (working on C with intersection of sets would be too hardcore, although probably faster). The source code is under a spoiler, it can be compiled in the free g ++ compiler, the code works under Windows, OSX and even on Raspberry Pi.
For those who are too lazy to install the C ++ compiler, a slightly optimized Python version is shown, which can be run in any online editor (I used https://repl.it/languages/python ).
There are very few a, b, c tracks.
Some results are shown below:
N = 10 : 1 “troika”, execution time <0.001c
1 + 8 = 9
N = 100 : 2 “triples”, execution time <0.001c
1 + 8 = 9
1 + 80 = 81
N = 1000 : 8 "triples", execution time <0.01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625
N = 10000 : 23 "triples", runtime 2s
N = 100000 : 53 "triples", run time 50c
With N = 1,000,000, we have only 102 “triples”, the full list is given under the spoiler.
Alas, the program still works slowly, I didn’t wait for the results for N = 10,000,000, the calculation time is more than an hour (maybe I was mistaken somewhere with the optimization of the algorithm, and it can be done better).
It is even more interesting to look at the results graphically:
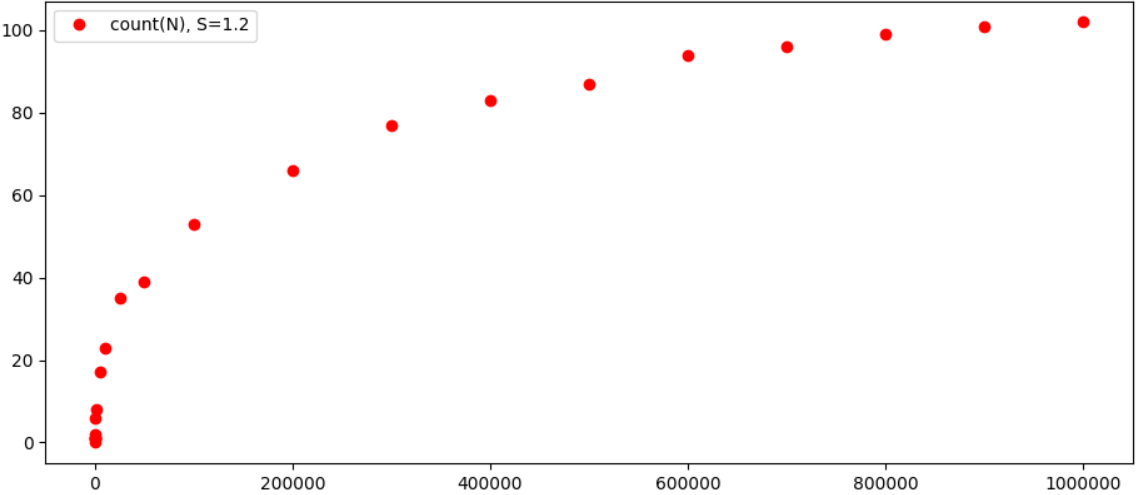
In principle, it is quite obvious that the dependence of the number of possible triples on N grows noticeably slower than N itself, and it is quite likely that the result will converge to some specific number for each ε. By the way, as ε increases, the number of “triples” decreases noticeably, for example, when ε = 0.4, we have only 2 equalities for N <100000 (1 + 4374 = 4375 and 343 + 59049 = 59392). So in general, it seems that the theorem is indeed satisfied (well, and probably it has already been tested on computers more powerful, and it is possible that all this has long been calculated).
Those interested can experiment on their own, if anyone has results for numbers 10,000,000 or more, I’m happy to add them to the article. Of course, it would be interesting to “calculate” until the moment when the set of “triples” stops growing completely, but it can take a really long time, the speed of calculation seems to depend on N as N * N (and maybe N ^ 3), and the process very long. Nevertheless, an amazing number, and those who wish may well join the search.
Edit: as suggested in the comments, the table with the results already exists in Wikipedia - in the range N up to 10 ^ 18 the number of "triples" is still growing, so the "end" of the set has not yet been found. The more interesting - the intrigue is still preserved.
On
Without claiming Mochizuki’s laurels, I
Who cares what happened, I ask for cat.
Formulation of the problem
Start over. What is the theorem about? As Wikipedia says (the wording in the English version is a little more understandable), for mutually simple (without common divisors) numbers a, b and c, such that a + b = c, for any ε> 0 there is a limited number of triples a + b = c, such that:
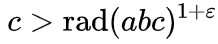
The function rad is called the radical , and denotes the product of prime factors of a number. For example, rad (16) = rad (2 * 2 * 2 * 2) = 2, rad (17) = 17 (17 is a prime number), rad (18) = rad (2 * 3 * 3) = 2 * 3 = 6, rad (1,000,000) = rad (2 ^ 6 ⋅ 5 ^ 6) = 2 * 5 = 10.
Actually, the essence of the theorem is that the number of such triples is quite small. For example, if we take at random ε = 0.2 and equality 100 + 27 = 127: rad (100) = rad (2 * 2 * 5 * 5) = 10, rad (27) = rad (3 * 3 * 3) = 3, rad (127) = 127, rad (a * b * c) = rad (a) * rad (b) * rad (s) = 3810, 3810 ^ 1.2 is clearly greater than 127, the inequality is not satisfied. But there are exceptions, for example, for equality 49 + 576 = 625, the condition of the theorem is fulfilled (those who wish can check it themselves).
The next key moment for us is of these equalities, according to the theorem, a limited number. Those. This means that you can just try them all on your computer. In the end, this gives us the
So let's get started.
Source
The first version was written in Python, and although this language is too slow for such calculations, writing code on it is easy and simple, which is convenient for prototyping.
Getting the radical : decompose the number into prime factors, then remove the repetitions, converting the array into a set. Then we just get the product of all the elements.
defprime_factors(n):
factors = []
# Print the number of two's that divide nwhile n % 2 == 0:
factors.append(int(2))
n = n / 2# n must be odd at this point so a skip of 2 ( i = i + 2) can be usedfor i in range(3, int(math.sqrt(n)) + 1, 2):
# while i divides n , print i ad divide nwhile n % i == 0:
factors.append(int(i))
n = n / i
# Condition if n is a prime number greater than 2if n > 2:
factors.append(int(n))
return set(factors)
defrad(n):
result = 1for num in prime_factors(n):
result *= num
return result
Mutually simple numbers : decompose numbers into factors, and just check the intersection of sets.
defnot_mutual_primes(a,b,c):
fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c)
return len(fa.intersection(fb)) == 0and len(fa.intersection(fc)) == 0and len(fb.intersection(fc)) == 0Check : we use already created functions, everything is simple.
defcheck(a,b,c):
S = 1.2# Eps=0.2if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c):
print("{} + {} = {} - PASSED".format(a, b, c))
else:
print("{} + {} = {} - FAILED".format(a, b, c))
check(10, 17, 27)
check(49, 576, 625)
Those interested can experiment on their own by copying the above code into any online Python editor. Of course, the code works as expectedly slowly, and going through all the triples to at least a million would be too long. Below is a optimized version under the spoiler, it is recommended to use it.
The final version was rewritten in C ++ using multithreading and some optimization (working on C with intersection of sets would be too hardcore, although probably faster). The source code is under a spoiler, it can be compiled in the free g ++ compiler, the code works under Windows, OSX and even on Raspberry Pi.
C ++ Code
// To compile: g++ abc.cpp -O3 -fopenmp -oabc#include<string.h>#include<math.h>#include<stdbool.h>#include<stdint.h>#include<stdio.h>#include<vector>#include<set>#include<map>#include<algorithm>#include<time.h>typedefunsignedlongint valType;
typedefstd::vector<valType> valList;
typedefstd::set<valType> valSet;
typedef valList::iterator valListIterator;
std::vector<valList> valFactors;
std::vector<double> valRads;
valList factors(valType n){
valList results;
valType z = 2;
while (z * z <= n) {
if (n % z == 0) {
results.push_back(z);
n /= z;
} else {
z++;
}
}
if (n > 1) {
results.push_back(n);
}
return results;
}
valList unique_factors(valType n){
valList results = factors(n);
valSet vs(results.begin(), results.end());
valList unique(vs.begin(), vs.end());
std::sort(unique.begin(), unique.end());
return unique;
}
doublerad(valType n){
valList f = valFactors[n];
double result = 1;
for (valListIterator it=f.begin(); it<f.end(); it++) {
result *= *it;
}
return result;
}
boolnot_mutual_primes(valType a, valType b, valType c){
valList res1 = valFactors[a], res2 = valFactors[b], res3; // = valFactors[c];
valList c12, c13, c23;
set_intersection(res1.begin(),res1.end(), res2.begin(),res2.end(), back_inserter(c12));
if (c12.size() != 0) returnfalse;
res3 = valFactors[c];
set_intersection(res1.begin(),res1.end(), res3.begin(),res3.end(), back_inserter(c13));
if (c13.size() != 0) returnfalse;
set_intersection(res2.begin(),res2.end(), res3.begin(),res3.end(), back_inserter(c23));
return c23.size() == 0;
}
intmain(){
time_tstart_t, end_t;
time(&start_t);
int cnt=0;
double S = 1.2;
valType N_MAX = 10000000;
printf("Getting prime factors...\n");
valFactors.resize(2*N_MAX+2);
valRads.resize(2*N_MAX+2);
for(valType val=1; val<=2*N_MAX+1; val++) {
valFactors[val] = unique_factors(val);
valRads[val] = rad(val);
}
time(&end_t);
printf("Done, T = %.2fs\n", difftime(end_t, start_t));
printf("Calculating...\n");
#pragma omp parallel for reduction(+:cnt)for(int a=1; a<=N_MAX; a++) {
for(int b=a; b<=N_MAX; b++) {
int c = a+b;
if (c > pow(valRads[a]*valRads[b]*valRads[c], S) && not_mutual_primes(a,b,c)) {
printf("%d + %d = %d\n", a,b,c);
cnt += 1;
}
}
}
printf("Done, cnt=%d\n", cnt);
time(&end_t);
floatdiff_t = difftime(end_t, start_t);
printf("N=%lld, T = %.2fs\n", N_MAX, diff_t);
}
For those who are too lazy to install the C ++ compiler, a slightly optimized Python version is shown, which can be run in any online editor (I used https://repl.it/languages/python ).
Python version
from __future__ import print_function
import math
import time
import multiprocessing
prime_factors_list = []
rad_list = []
defprime_factors(n):
factors = []
# Print the number of two's that divide nwhile n % 2 == 0:
factors.append(int(2))
n = n / 2# n must be odd at this point so a skip of 2 ( i = i + 2) can be usedfor i in range(3, int(math.sqrt(n)) + 1, 2):
# while i divides n , print i ad divide nwhile n % i == 0:
factors.append(int(i))
n = n / i
# Condition if n is a prime number greater than 2if n > 2:
factors.append(int(n))
return factors
defrad(n):
result = 1for num in prime_factors_list[n]:
result *= num
return result
defnot_mutual_primes(a,b,c):
fa, fb, fc = prime_factors_list[a], prime_factors_list[b], prime_factors_list[c]
return len(fa.intersection(fb)) == 0and len(fa.intersection(fc)) == 0and len(fb.intersection(fc)) == 0defcalculate(N):
S = 1.2
cnt = 0for a in range(1, N):
for b in range(a, N):
c = a+b
if c > (rad_list[a]*rad_list[b]*rad_list[c])**S and not_mutual_primes(a, b, c):
print("{} + {} = {}".format(a, b, c))
cnt += 1
print("N: {}, CNT: {}".format(N, cnt))
return cnt
if __name__ == '__main__':
t1 = time.time()
NMAX = 100000
prime_factors_list = [0]*(2*NMAX+2)
rad_list = [0]*(2*NMAX+2)
for p in range(1, 2*NMAX+2):
prime_factors_list[p] = set(prime_factors(p))
rad_list[p] = rad(p)
calculate(NMAX)
print("Done", time.time() - t1)
results
There are very few a, b, c tracks.
Some results are shown below:
N = 10 : 1 “troika”, execution time <0.001c
1 + 8 = 9
N = 100 : 2 “triples”, execution time <0.001c
1 + 8 = 9
1 + 80 = 81
N = 1000 : 8 "triples", execution time <0.01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625
N = 10000 : 23 "triples", runtime 2s
Triplets A, B, C up to 10,000
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
3 + 125 = 128
5 + 1024 = 1029
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
49 + 576 = 625
1331 + 9604 = 10935
81 + 1250 = 1331
125 + 2187 = 2312
243 + 1805 = 2048
289 + 6272 = 6561
625 + 2048 = 2673N = 100000 : 53 "triples", run time 50c
Three A, B, C to 100,000
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
1 + 12167 = 12168
1 + 14336 = 14337
1 + 57121 = 57122
1 + 59048 = 59049
1 + 71874 = 71875
3 + 125 = 128
3 + 65533 = 65536
5 + 1024 = 1029
7 + 32761 = 32768
9 + 15616 = 15625
9 + 64000 = 64009
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
28 + 50625 = 50653
31 + 19652 = 19683
37 + 32768 = 32805
49 + 576 = 625
49 + 16335 = 16384
73 + 15552 = 15625
81 + 1250 = 1331
121 + 12167 = 12288
125 + 2187 = 2312
125 + 50176 = 50301
128 + 59049 = 59177
169 + 58880 = 59049
243 + 1805 = 2048
243 + 21632 = 21875
289 + 6272 = 6561
343 + 59049 = 59392
423 + 16384 = 16807
507 + 32768 = 33275
625 + 2048 = 2673
1331 + 9604 = 10935
1625 + 16807 = 18432
28561 + 89088 = 117649
28561 + 98415 = 126976
3584 + 14641 = 18225
6561 + 22000 = 28561
7168 + 78125 = 85293
8192 + 75843 = 84035
36864 + 41261 = 78125With N = 1,000,000, we have only 102 “triples”, the full list is given under the spoiler.
Three A, B, C up to 1,000,000
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
1 + 12167 = 12168
1 + 14336 = 14337
1 + 57121 = 57122
1 + 59048 = 59049
1 + 71874 = 71875
1 + 137780 = 137781
1 + 156249 = 156250
1 + 229375 = 229376
1 + 263168 = 263169
1 + 499999 = 500000
1 + 512000 = 512001
1 + 688127 = 688128
3 + 125 = 128
3 + 65533 = 65536
5 + 1024 = 1029
5 + 177147 = 177152
7 + 32761 = 32768
9 + 15616 = 15625
9 + 64000 = 64009
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
13 + 421875 = 421888
17 + 140608 = 140625
25 + 294912 = 294937
28 + 50625 = 50653
31 + 19652 = 19683
37 + 32768 = 32805
43 + 492032 = 492075
47 + 250000 = 250047
49 + 576 = 625
49 + 16335 = 16384
49 + 531392 = 531441
64 + 190269 = 190333
73 + 15552 = 15625
81 + 1250 = 1331
81 + 123823 = 123904
81 + 134375 = 134456
95 + 279841 = 279936
121 + 12167 = 12288
121 + 255879 = 256000
125 + 2187 = 2312
125 + 50176 = 50301
128 + 59049 = 59177
128 + 109375 = 109503
128 + 483025 = 483153
169 + 58880 = 59049
243 + 1805 = 2048
243 + 21632 = 21875
289 + 6272 = 6561
338 + 390625 = 390963
343 + 59049 = 59392
423 + 16384 = 16807
507 + 32768 = 33275
625 + 2048 = 2673
864 + 923521 = 924385
1025 + 262144 = 263169
1331 + 9604 = 10935
1375 + 279841 = 281216
1625 + 16807 = 18432
2197 + 583443 = 585640
2197 + 700928 = 703125
3481 + 262144 = 265625
3584 + 14641 = 18225
5103 + 130321 = 135424
6125 + 334611 = 340736
6561 + 22000 = 28561
7153 + 524288 = 531441
7168 + 78125 = 85293
8192 + 75843 = 84035
8192 + 634933 = 643125
9583 + 524288 = 533871
10816 + 520625 = 531441
12005 + 161051 = 173056
12672 + 117649 = 130321
15625 + 701784 = 717409
18225 + 112847 = 131072
19683 + 228125 = 247808
24389 + 393216 = 417605
28561 + 89088 = 117649
28561 + 98415 = 126976
28561 + 702464 = 731025
32768 + 859375 = 892143
296875 + 371293 = 668168
36864 + 41261 = 78125
38307 + 371293 = 409600
303264 + 390625 = 693889
62192 + 823543 = 885735
71875 + 190269 = 262144
131072 + 221875 = 352947
132651 + 588245 = 720896
Alas, the program still works slowly, I didn’t wait for the results for N = 10,000,000, the calculation time is more than an hour (maybe I was mistaken somewhere with the optimization of the algorithm, and it can be done better).
It is even more interesting to look at the results graphically:

In principle, it is quite obvious that the dependence of the number of possible triples on N grows noticeably slower than N itself, and it is quite likely that the result will converge to some specific number for each ε. By the way, as ε increases, the number of “triples” decreases noticeably, for example, when ε = 0.4, we have only 2 equalities for N <100000 (1 + 4374 = 4375 and 343 + 59049 = 59392). So in general, it seems that the theorem is indeed satisfied (well, and probably it has already been tested on computers more powerful, and it is possible that all this has long been calculated).
Those interested can experiment on their own, if anyone has results for numbers 10,000,000 or more, I’m happy to add them to the article. Of course, it would be interesting to “calculate” until the moment when the set of “triples” stops growing completely, but it can take a really long time, the speed of calculation seems to depend on N as N * N (and maybe N ^ 3), and the process very long. Nevertheless, an amazing number, and those who wish may well join the search.
Edit: as suggested in the comments, the table with the results already exists in Wikipedia - in the range N up to 10 ^ 18 the number of "triples" is still growing, so the "end" of the set has not yet been found. The more interesting - the intrigue is still preserved.
