April 10, 2015 at 17:04Draw an ellipse at an arbitrary angle in canvas in JavaScript
- Tutorial
In the process of developing one application, I was faced with the need to draw ellipses at an arbitrary angle in canvas in JavaScript. I didn’t want to use any frameworks in such a simple project, so I went in search of a manual article on this topic. The searches were unsuccessful, so I had to deal with the task myself, and I decided to share the experience with you.
We formalize the problem. We need the drawEllipse (coords, sizes, vector) function , where:
The article provides three ways to solve this problem.
Bezier curves were chosen as the first method. To construct such a curve, four points are required: a start, an end, and two control points.
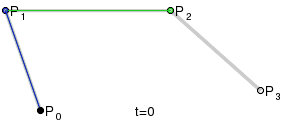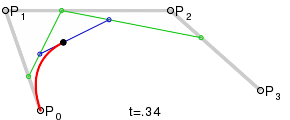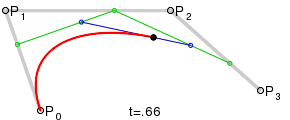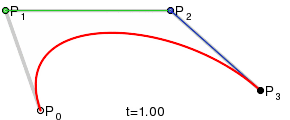
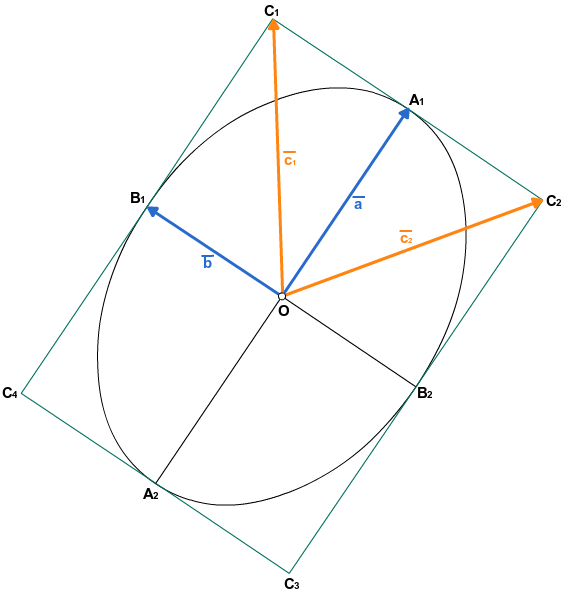
The desired ellipse will consist of two such curves, and it is easy to guess that the above points at each of them will be the vertices of the rectangle. Let's explore our ellipse.
Actually demo and code:
Upd. After reviewing the comments, he wrote the function of drawing an ellipse through a parametric equation, and it turned out that the figure obtained using Bezier curves does not exactly coincide with the ellipse. On the overlay of figures, it can be seen that the object (red) drawn by Bezier curves is sometimes wider than the regular ellipse (blue). Here is a demo of overlapping shapes.
Upd. The comments suggested a more native and simple way to draw an oblique ellipse (thanks subzey ). I’ll leave here so as not to get lost. Here is a demo .
We formalize the problem. We need the drawEllipse (coords, sizes, vector) function , where:
- coords - coordinates of the center of the ellipse - array [x, y]
- sizes - lengths of the major and minor semiaxes of the ellipse - array [a, b]
- vector - the vector [x, y] of the slope of the ellipse
The article provides three ways to solve this problem.
Bezier curves were chosen as the first method. To construct such a curve, four points are required: a start, an end, and two control points.
The desired ellipse will consist of two such curves, and it is easy to guess that the above points at each of them will be the vertices of the rectangle. Let's explore our ellipse.
- We have some vector.
Find the unit vector.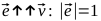
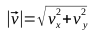
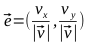
Find the unit vector.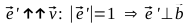
To do this, recall the property of the scalar product of the vectors to vanish if they are perpendicular: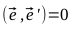
Thus: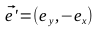
- Find the vectors
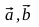, points A 1 , A 2 , B 1 , B 2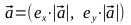
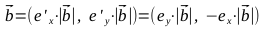
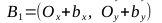
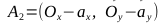
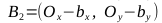
- Find the vectors
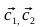, points C 1 , C 2 , C 3 , C 4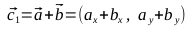
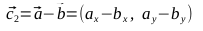
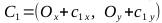
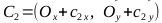
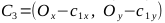
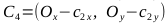
- Recall that to draw an ellipse we need two Bezier curves:
- 1st has a starting point B 1 , ending B 2 , passes through point A 1
- 2nd has a starting point B 2 , an end point B 1 , passes through point A 2
Let us depict the moment of construction of the Bezier curve at the point at which it (the curve) will be closest to the segment between the control points. In our case, it will look like this: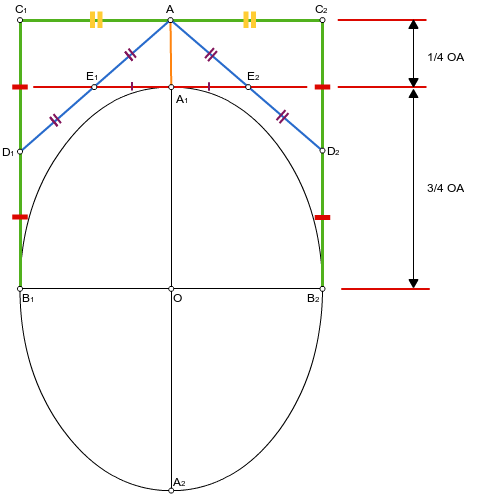
From the figure it is obvious that the distance from this point (A 1 ) to the segment between the control points (C 1 , C 2 ) will be a quarter of the distance between the center of the desired ellipse (O) and the same segment ( C 1, C 2 ), i.e.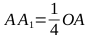
- Denote OA by x. We solve the equation
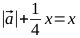
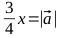
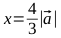
Thus, to obtain an ellipse with the necessary parameters, we need to multiply the vector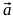
by the parameter 
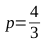, and then return to the calculations described in paragraphs 1-4. As a result, we obtain sets of points ( B 1 , C 1 , C 2 , B 2 and B 2 , C 3 , C 4 , B 1 ) for constructing two Bezier curves that together represent the desired shape.
Actually demo and code:
function drawEllipse(ctx, coords, sizes, vector) {
var vLen = Math.sqrt(vector[0]*vector[0]+vector[1]*vector[1]); // вычисляем длину вектора
var e = [vector[0]/vLen, vector[1]/vLen]; // единичный верктор e || vector
var p = 4/3; // параметр
var a = [e[0]*sizes[0]*p, e[1]*sizes[0]*p]; // находим вектор a, используя параметр
var b = [e[1]*sizes[1], -e[0]*sizes[1]]; // находм вектор b
// находим точки A1, B1, A2, B2
var dotA1 = [coords[0]+a[0], coords[1]+a[1]];
var dotB1 = [coords[0]+b[0], coords[1]+b[1]];
var dotA2 = [coords[0]-a[0], coords[1]-a[1]];
var dotB2 = [coords[0]-b[0], coords[1]-b[1]];
// находим вектора c1, c2
var c1 = [a[0]+b[0], a[1]+b[1]];
var c2 = [a[0]-b[0], a[1]-b[1]];
// находим точки C1, C2, C3, C4
var dotC1 = [coords[0]+c1[0], coords[1]+c1[1]];
var dotC2 = [coords[0]+c2[0], coords[1]+c2[1]];
var dotC3 = [coords[0]-c1[0], coords[1]-c1[1]];
var dotC4 = [coords[0]-c2[0], coords[1]-c2[1]];
// рисуем наш эллипс
ctx.strokeStyle = 'black';
ctx.beginPath();
ctx.moveTo(dotB1[0], dotB1[1]); // начальная точка
ctx.bezierCurveTo(dotC1[0], dotC1[1], dotC2[0], dotC2[1], dotB2[0], dotB2[1]); // рисуем кривую Безье
ctx.bezierCurveTo(dotC3[0], dotC3[1], dotC4[0], dotC4[1], dotB1[0], dotB1[1]); // и вторую из точки, где закончили рисовать первую
ctx.stroke();
ctx.closePath();
// возвращаем вектору a изначальную длину
a = [e[0]*sizes[0], e[1]*sizes[0]];
// отрисовываем красным большую и малую оси эллипса, чтобы проверить, правильно ли мы отобразили запрошенный эллипс
ctx.beginPath();
ctx.moveTo(coords[0]+a[0], coords[1]+a[1]);
ctx.lineTo(coords[0]-a[0], coords[1]-a[1]);
ctx.moveTo(coords[0]+b[0], coords[1]+b[1]);
ctx.lineTo(coords[0]-b[0], coords[1]-b[1]);
ctx.strokeStyle = 'red';
ctx.stroke();
ctx.closePath();
}
Upd. After reviewing the comments, he wrote the function of drawing an ellipse through a parametric equation, and it turned out that the figure obtained using Bezier curves does not exactly coincide with the ellipse. On the overlay of figures, it can be seen that the object (red) drawn by Bezier curves is sometimes wider than the regular ellipse (blue). Here is a demo of overlapping shapes.
function drawEllipseParam(ctx, coords, sizes, angle, segments) {
ctx.save();
ctx.translate(coords[0], coords[1]);
ctx.rotate(angle);
ctx.beginPath();
var x, y, firstTime=true;
var dt = 2*Math.PI/segments;
for(var t=0; t<2*Math.PI; t+=dt) {
x = sizes[0]*Math.cos(t);
y = sizes[1]*Math.sin(t);
if(firstTime) {
firstTime = false;
ctx.moveTo(x, y);
} else {
ctx.lineTo(x, y);
}
}
ctx.strokeStyle = 'blue';
ctx.stroke();
ctx.closePath();
ctx.restore();
}
Upd. The comments suggested a more native and simple way to draw an oblique ellipse (thanks subzey ). I’ll leave here so as not to get lost. Here is a demo .
function drawEllipse(ctx, coords, sizes, angle) {
ctx.beginPath();
ctx.save(); // сохраняем стейт контекста
ctx.translate(coords[0], coords[1]); // перемещаем координаты в центр эллипса
ctx.rotate(angle); // поворачиваем координатную сетку на нужный угол
ctx.scale(1, sizes[1]/sizes[0]); // сжимаем по вертикали
ctx.arc(0, 0, sizes[0], 0, Math.PI*2); // рисуем круг
ctx.restore(); // восстанавливает стейт, иначе обводка и заливка будут сплющенными и повёрнутыми
ctx.strokeStyle = 'green';
ctx.stroke(); // обводим
ctx.closePath();
}