Deep Learning, NLP, and Representations
I offer readers of Habrahabr a translation of the post “Deep Learning, NLP, and Representations” by the cool Christopher Olah. Illustrations from there.
In recent years, methods using deep neural networks have taken a leading position in pattern recognition. Thanks to them, the bar for the quality of computer vision methods has risen significantly. Speech recognition is moving in the same direction.
Results are results, but why do they solve problems so cool?
The post highlights some of the impressive results of using deep neural networks in Natural Language Processing (NLP). Thus, I hope to lucidly state one of the answers to the question why deep neural networks work .
A neural network with a hidden layer is universal: with a sufficiently large number of hidden nodes, it can build an approximation of any function. There is a frequently quoted (and even more often incorrectly understood and applied) theorem about this.
This is true because the hidden layer can simply be used as a “lookup table".
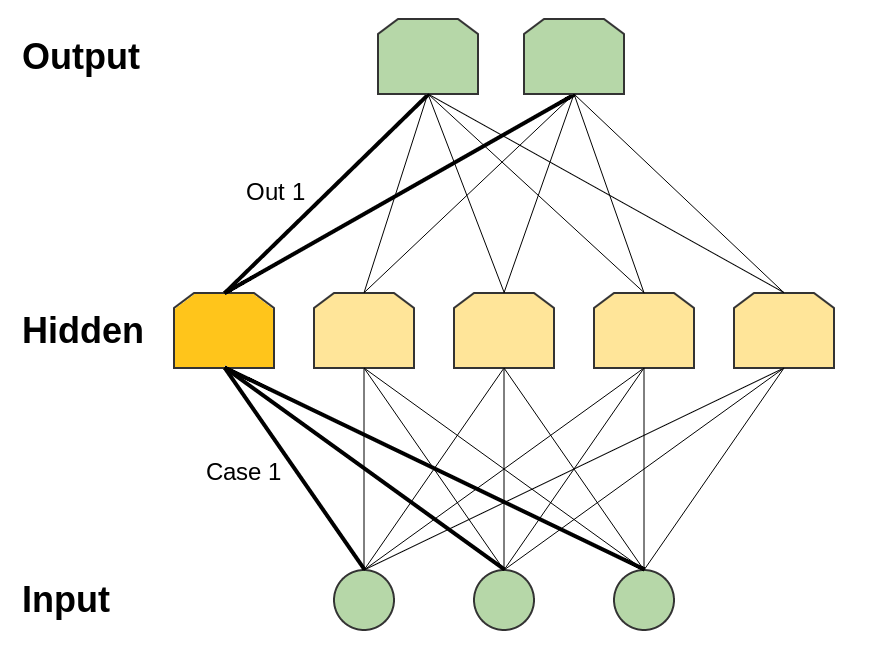
For simplicity, consider the perceptron. This is a very simple neuron that fires if its value exceeds a threshold value, and does not fire if not. The perceptron has binary inputs and a binary output (i.e. 0 or 1). The number of input value options is limited. Each of them can be associated with a neuron in a hidden layer that works only for a given input.
Analysis of the “condition” for each individual input will require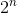
hidden neurons (for ndata). In fact, usually it’s not so bad. There may be “conditions” under which several input values are suitable, and there may be “overlapping” “conditions” that reach the correct inputs at their intersection.
Then we can use the connections between this neuron and the output neurons to set the final value for this particular case.
Universality is possessed not only by perceptrons. Networks with sigmoid cells in neurons (and other activation functions) are also universal: with a sufficient number of hidden neurons, they can build an arbitrarily accurate approximation of any continuous function. It is much more difficult to demonstrate this, since you cannot just take and isolate the inputs from each other.
Therefore, it turns out that neural networks with one hidden layer are actually universal. However, this is not impressive or surprising. The fact that the model can work as a look-up table is not the strongest argument in favor of neural networks. This just means that the model is basically capable of coping with the task. By universality we mean only that the network can adapt to any samples, but this does not mean that it is able to adequately interpolate the solution for working with new data.
No, versatility does not yet explain why neural networks work so well. The correct answer lies a little deeper. To understand, we first consider a few specific results.
I'll start with a particularly interesting sub-area of deep learning - with vector representations of words (word embeddings). In my opinion, vector representations are now one of the coolest topics for research in deep learning, although they were first proposed by Bengio, et al. more than 10 years ago.
Vector representations were first proposed by Bengio et al, 2001 and Bengio et al, 2003 several years before the resurrection of deep learning in 2006, when neural networks were not yet in fashion. The idea of distributed representations as such is even older (see, for example, Hinton 1986 ).
In addition, I think that this is one of those tasks with which the best way to form an intuitive understanding of why deep learning is so effective.
A vector representation of a word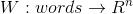
is a parameterized function that maps words from a certain natural language to large-dimension vectors (say, from 200 to 500 dimensions). For example, it may look like this:
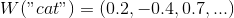
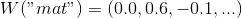
(As a rule, this function is defined by a lookup table defined by a matrix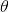
in which each word corresponds to a row 
).
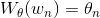W is initialized with random vectors for each word. She will be trained to give meaningful values to solve a problem.
For example, we can drag the network to determine if the 5-gram is “correct” (a five-word sequence, for example, 'cat sat on the mat'). 5 grams can be easily obtained from Wikipedia, and then half of them are “spoiled”, replacing each of some of the words with a random one (for example, 'cat sat song the mat'), since this almost always makes the 5 gram meaningless .
A modular network to determine if a 5-gram is “correct” ( Bottou (2011) ).
The model that we train will pass each 5-gram word through W , receiving their vector representations at the output, and feed them to another module, R , which will try to predict whether the 5-gram is “correct” or not. We want it to be this way:
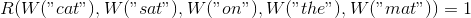
In order to predict these values accurately, the network needs to select parameters for W and R well .
However, this task is boring. Probably, the solution found will help to find grammatical errors in the texts or something like that. But what's really valuable, since it obtained the W .
(In fact, all the salt of the assignment in trainingThe W . We could consider solutions to other problems; so, one of the most common is the prediction of the next word in a sentence. But this is not our goal now. In the remainder of this section, we will talk about many of the results of the vector representation of words and will not be distracted by highlighting the difference between the approaches).
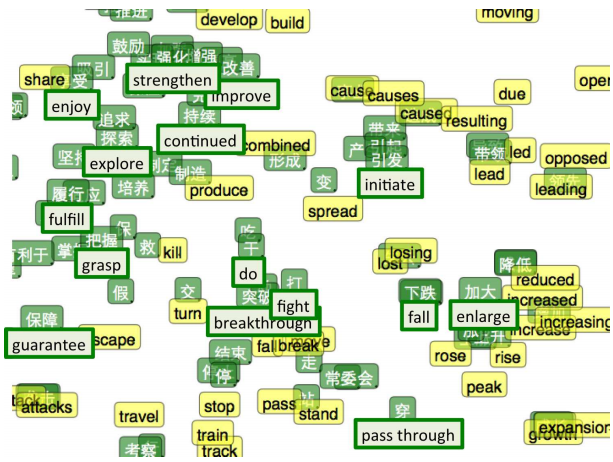
To "feel" how the space of vector representations is arranged, you can depict them using the tricky method of visualizing high-dimensional data - tSNE.
Visualization of vector representations of words using tSNE. On the left is the “area of numbers”, on the right is the “area of professions” (from Turian et al. (2010) ).
Such a “word map” seems quite meaningful. “Similar” words are close, and if you look at which ideas are closer to the others, it turns out that at the same time, close ones are “similar”.
Whose vector representations are closer to the representation of a given word? ( Collobert et al. (2011) .)
It seems natural that a network matches words with similar meanings to close vectors. If you replace the word with a synonym (“some sing well”,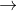
“few sing well”), then the “correctness” of the sentence does not change. It would seem that the input sentences differ significantly, but since W “shifts” the representations of synonyms (“some” and “few”) to each other, little changes for R.
This is a powerful tool. The number of possible 5 grams is huge, while the size of the training sample is relatively small. The convergence of representations of similar words allows us, taking one sentence, how to work with a whole class of "similar" ones. The case is not limited to replacing synonyms, for example, it is possible to substitute a word from the same class (“wall blue”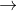“wall red”). Moreover, it makes sense to replace several words at the same time (“blue wall”, 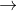“red ceiling”). The number of such “similar phrases” is growing exponentially from the number of words.
Already in the fundamental work of A Neural Probabilistic Language Model (Bengio, et al. 2003), substantial explanations are given why vector representations are such a powerful tool.
Obviously, this property is Wwould be very helpful. But how is she taught? It is very likely that many times W encounters the sentence “wall blue” and recognizes it as correct before seeing the sentence “wall red”. Shifting “red” closer to “blue” improves network performance.
We still need to deal with examples of uses of each word, but analogies allow us to generalize to new combinations of words. With all the words whose meaning we understand, we have come across before, but the meaning of the sentence can be understood without ever hearing it before. Neural networks can do the same.
Mikolov et al. (2013a)
Vector representations have another much more remarkable property: it seems that the analogy relations between words are determined by the value of the difference vector between their representations. For example, judging by everything, the difference vector of “male-female” words is constant:
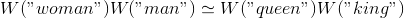
Maybe it won’t surprise anyone. In the end, the presence of pronouns of the genus suggests that replacing the word "kills" the grammatical correctness of the sentence. We write: “she is an aunt,” but “he is an uncle.” Similarly, "he is the king" and "she is the queen." If we see in the text “she is uncle”, most likely this is a grammatical error. If in half the cases the words were replaced randomly, then this must be our case.
"Of course!" - we say, looking back at past experience. “Vector representations will be able to represent gender. Surely there is a separate dimension for the floor. And also for the plural / singular. Yes, such relationships are easily recognized! ”
It turns out, however, that much more complex relationships are “coded” similarly. Just miracles in the sieve (well, almost)!
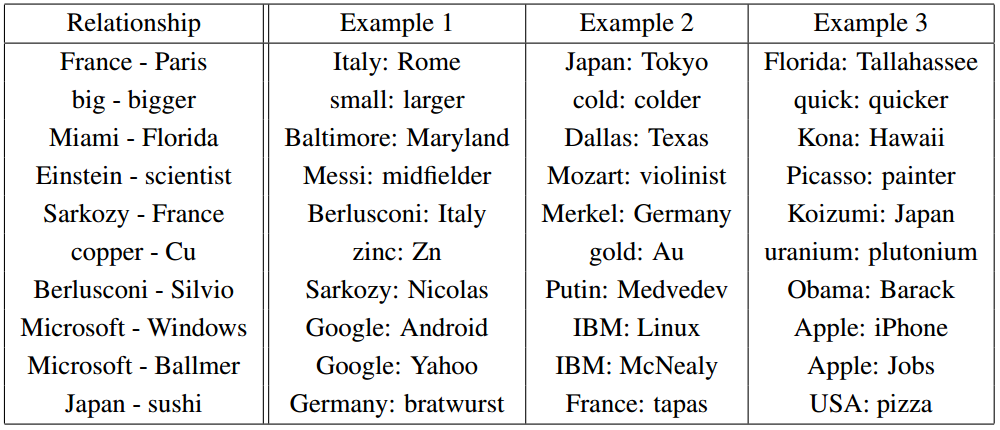
Relationship Pairs (from Mikolov et al. (2013b) .)
It is important that all of these W properties are side effects. We did not impose requirements that representations of similar words should be close to each other. We did not try to adjust the analogies ourselves with the help of vector differences. We just tried to learn how to check whether the proposal is “correct”, and the properties came from somewhere in the process of solving the optimization problem.
The great strength of neural networks seems to be that they automatically learn to build the “best” representations of the data. In turn, data presentation is an essential part of solving many machine learning problems. And vector representations of words is one of the most amazing examples of learning a representation.
The properties of vector representations are, of course, curious, but can we do something useful with their help? In addition to stupid little things like checking if a particular 5-gram is “correct”.
W and F train, driving task under A . Then G will be able to learn to solve the problem of Bed and , using the W .
We trained vector representations of words in order to cope with simple tasks well, but knowing their wonderful properties that we have already observed, we can assume that they will be useful for more general problems. In fact, vector representations like these are terribly important:
( Luong et al. (2013) .)
The general strategy is to train a good representation for Problem A and use it to solve Problem B - one of the main tricks in the deep learning magic hat. In different cases, it is called differently: pretraining, transfer learning, and multi-task learning. One of the strengths of this approach is that it allows you to train presentations on several types of data.
You can crank up this trick in a different way. Instead of adjusting the views for one data type and using them to solve problems of different types, you can display different types of data in a single view!
One of the great examples of using this trick is the vector representation of words for two languages proposed by Socher et al. (2013a) . We can learn to “embed” words from two languages into a single space. In this work, words from the English language and Putonghua (“Mandarin dialect” of Chinese) are “embedded”.
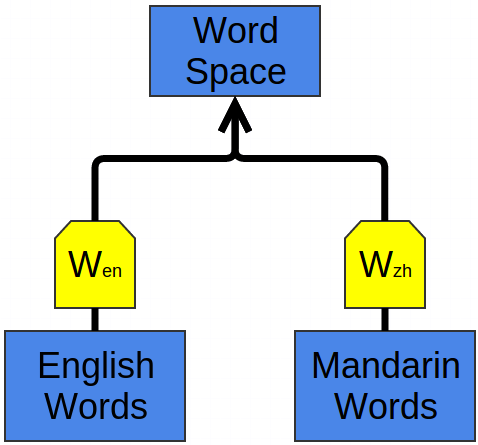
We train two vector representations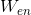
and 
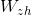in the same way as we did above. However, we know that some words in English and Chinese have similar meanings. So, we will optimize by one more criterion: the representations of the translations we know should be at a small distance from each other.
Of course, in the end we observe that the “similar” words known to us are stacked side by side. No wonder, because we have optimized so. What is much more interesting is this: translations that we did not know about are also nearby.
Perhaps this no longer surprises anyone in the light of our past experience with vector representations of words. They “attract” similar words to each other, therefore, if we know that English and Chinese words mean approximately the same thing, then the representations of their synonyms should be nearby. We also know that pairs of words in relationships like differences in gender (gender) differ by a constant vector. It seems that if you “pull together” a sufficient number of translations, you will be able to adjust the differences so that they are the same in two languages. As a result, if the "male versions" of the word in both languages are translated into each other, we automatically get that the "female versions" are also correctly translated.
Intuition suggests that languages must have a similar “structure” and that by forcibly linking them at the selected points, we pull up the rest of the ideas in the right places.
Visualization of bilingual vector representations using t-SNE. Chinese is highlighted in green, English is marked in yellow ( Socher et al. (2013a) ).
When dealing with two languages, we teach a common representation for two similar data types. But we can "fit" into a single space and very different types of data.
Recently, with the help of deep learning, they began to build models that “fit” images and words into a single space of representations.
In a previous work, we simulated the joint distribution of labels and images, but here it’s a bit different.
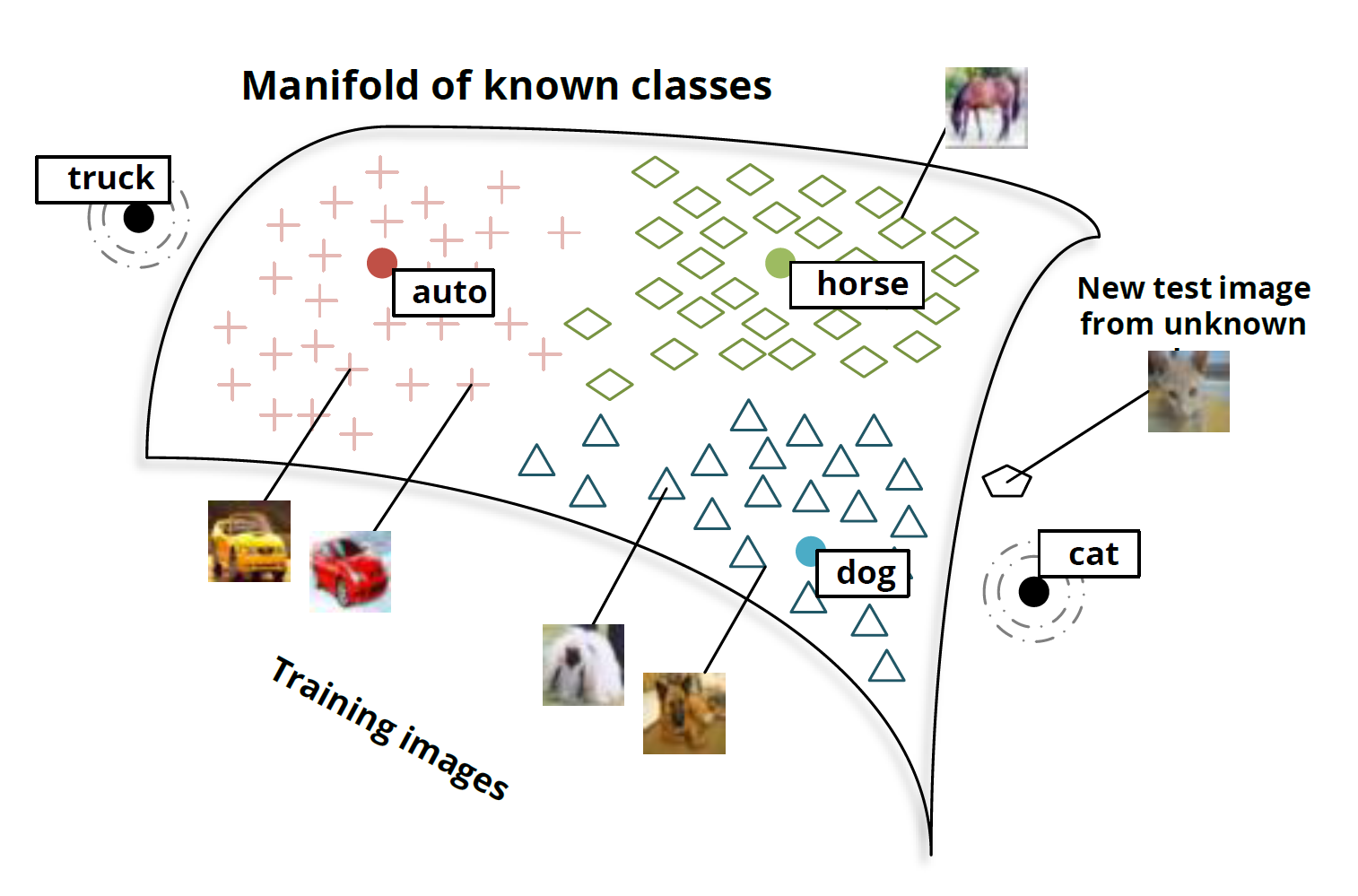
The main idea is that we classify images by issuing a vector from the space of word representations. Pictures with dogs are displayed in vectors near the representation of the word “dog”, with horses - about “horse”, with a car - about “car”. Etc.
The most interesting thing happens when you test a model on new image classes. So what will happen if we propose to classify the image of a cat seal of a model that was not taught to specifically recognize them, that is, to display it in a vector close to the “cat” vector?
Socher et al. (2013b)
It turns out that the network does a good job with new image classes. Images of cats are not displayed at random points in space. On the contrary, they fit in the vicinity of the "dog" vector and are pretty close to the "cat" vector. Similarly, truck images are displayed at points close to the “truck” vector, which is not far from the associated “car” vector.
Socher et al. (2013b)
Stanford group members did this with 8 known classes and two unknowns. The results are already impressive. But with such a small number of classes, there are not enough points on which the relationship between images and semantic space can be interpolated.
The Google research team has built a much larger version of the same; they took 1,000 categories instead of 8 - and at about the same time ( Frome et al. (2013) ), and then suggested another option ( Norouzi et al. (2014) ). The last two works are based on a strong model for classifying images ( Krizehvsky et al. (2012) ), but the images in them fit into the space of vector representations of words in different ways.
And the results are impressive. If it is not possible to accurately map the images of unknown classes to the correct vector, then at least it is possible to get into the right neighborhood. Therefore, if you try to classify images from unknown and significantly different categories, then at least classes can be distinguished.
Even if I have never seen a Aesculapian snake or an armadillo when their pictures are shown to me, I can tell who is shown where, because I have a general idea of what kind of appearance these animals can have. And such networks are also capable of this.
(We often used the phrase “these words are similar.” But it seems that much stronger results can be obtained based on the relationship between words. In our space of word representations, there is a constant difference between the “male” and “female versions.” But also in space Representations of images have reproducible properties that allow you to see the difference between the sexes.The beard, mustache and bald head are clearly recognizable signs of a man.Chest and long hair (a less reliable sign), makeup and jewelry are obvious indicators female I am well aware that the physical signs of the floor are deceptive, for example, I'm not going to say that all the bald -. men, or that all who have a bust - a woman, but that it is more likely true than not, help. we better set the initial values.
. Even if you have never seen a king, then when you see a queen (which you identified by the crown) with a beard, you will probably decide that you need to use the “masculine version” of the word “queen”).
General views (shared embeddings) - a breathtaking field of research; they are a very convincing argument in favor of promoting the training of ideas on the fronts of deep learning.
We started the discussion of vector representations of words with such a network:
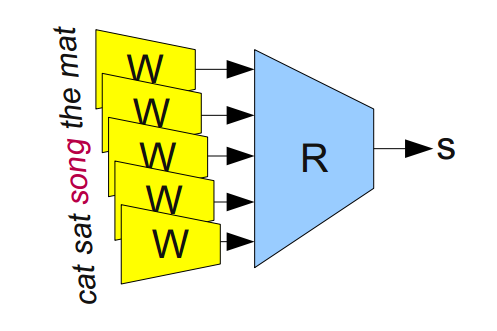
A Modular Network that teaches vector representations of words ( Bottou (2011) ).
The diagram shows a modular network
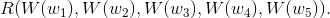
It is constructed from two modules, W and R . This approach to building neural networks - from smaller "neural network modules" - is not too widespread. However, he showed himself very well in the tasks of processing natural language.
The models that were described are strong, but they have one annoying limitation: the number of inputs they cannot change.
This can be dealt with by adding the associative module A , which “merges” the two vector representations.
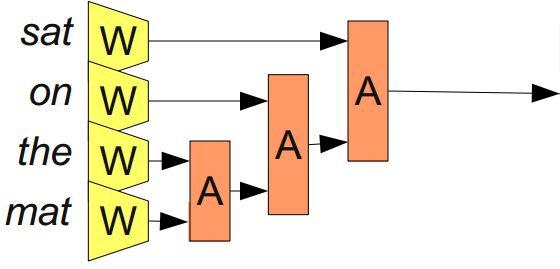
From Bottou (2011)
“Merging” word sequences, A allows you to represent phrases and even whole sentences. And since we want to "merge" a different number of words, the number of inputs should not be limited.
It is not a fact that it is correct to “merge” words in a sentence simply in order. The sentence 'the cat sat on the mat' can be decomposed into parts like this: '((the cat) (sat (on (the mat))'. We can apply A using this arrangement of brackets:
From Bottou (2011)
These models are often called recursive neural networks, since the output signal of one module is often fed to another module of the same type. Sometimes they are also called neural networks of a tree structure (tree-structured neural networks).
Recursive neural networks have achieved significant success in solving several problems of natural language processing. For example, in Socher et al. (2013c) they are used to predict sentiment sentence:
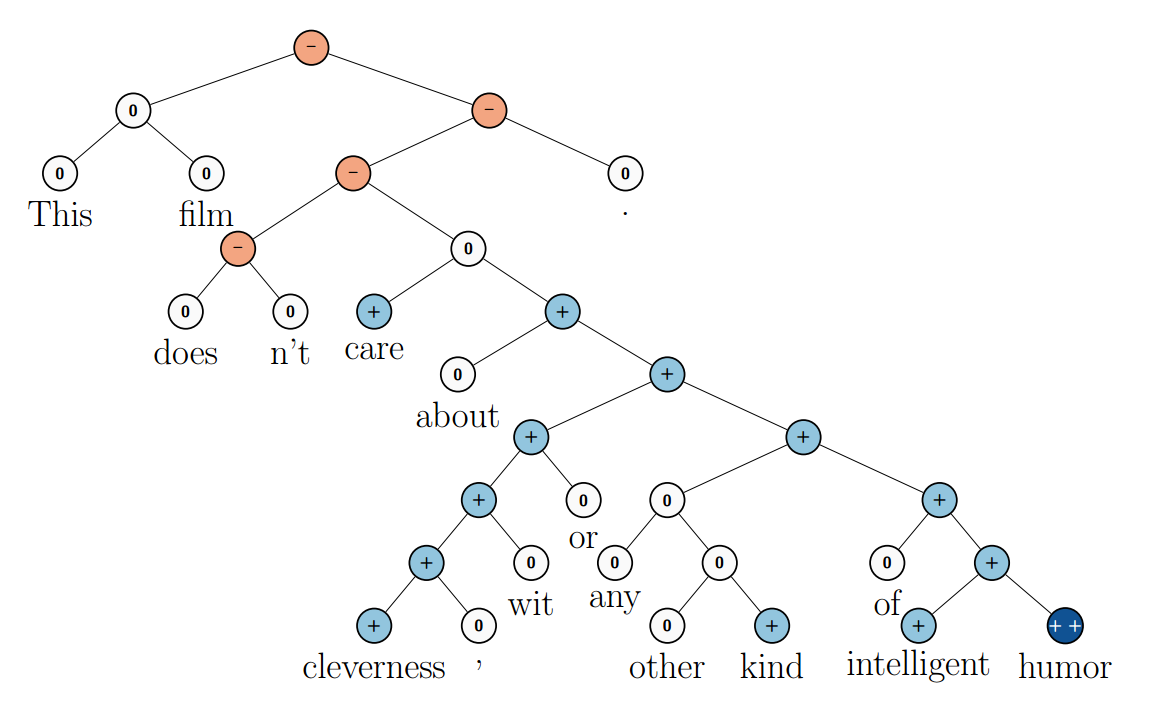
(From Socher et al. (2013c) .) The
main goal is to create a “reversible” representation of the proposal, that is, such that it can be reconstructed from the proposal with approximately the same value. For example, you can try to introduce a dissociative module D , which will perform the opposite action of A :
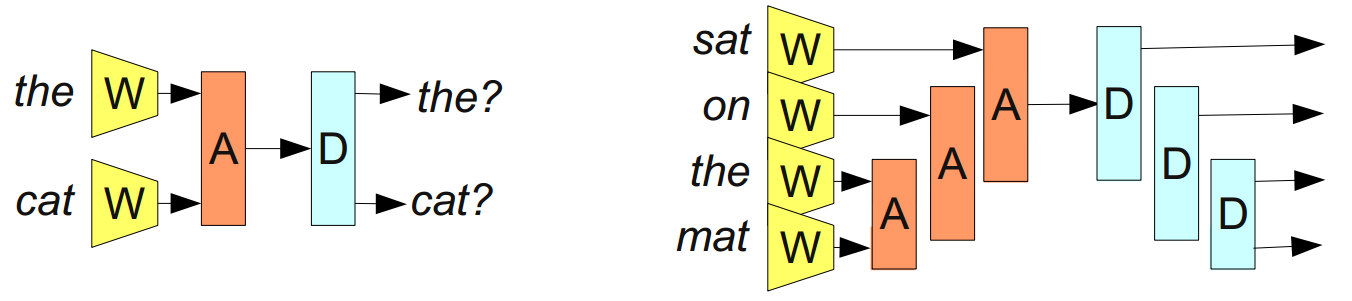
From Bottou (2011)
If it succeeds, then we will have an incredibly powerful tool on hand. For example, you can try to build proposal views for two languages and use it for automatic translation.
Unfortunately, it turns out to be very difficult. Terribly difficult. But, having received the basis for hope, many are struggling to solve the problem.
Recently, Cho et al. (2014) , progress has been made in the presentation of phrases, with a model that “encodes” a phrase in English and “decodes” it as a phrase in French. Just look what kind of performance comes out!
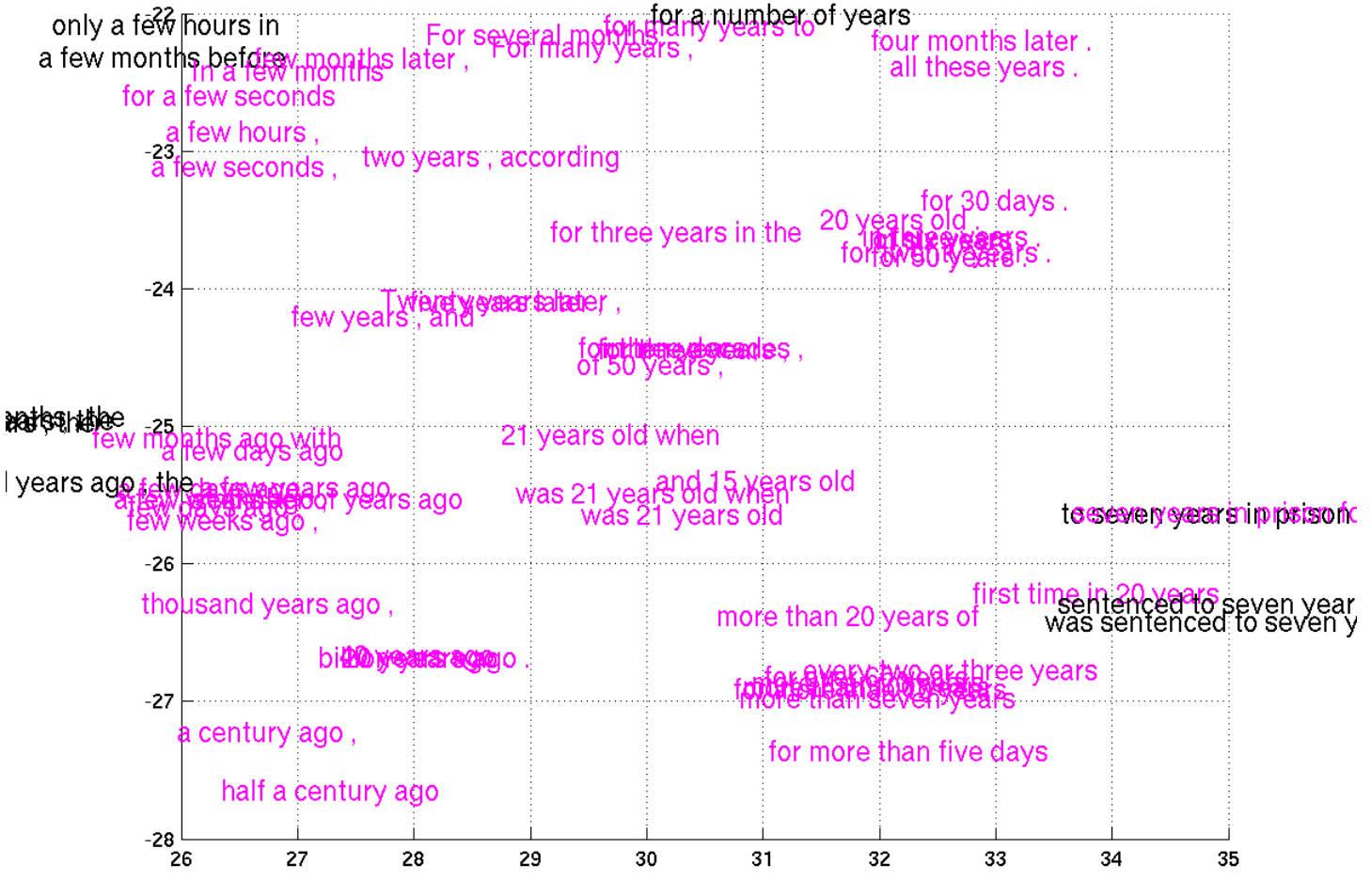
A small piece of representation space compressed with tSNE ( Cho et al. (2014) .)
I heard that some of the results discussed above were criticized by researchers from other areas, in particular, linguists and natural language processing specialists. It is not the results themselves that are criticized, but the consequences that are deduced from them, and the methods of comparison with other approaches.
I don’t think that I’m prepared so well to articulate exactly what the problem is. I would be glad if someone did this in the comments.
Deep learning in the service of learning representations is a powerful approach that seems to answer the question of why neural networks are so efficient. In addition, it has amazing beauty: why are neural networks effective? Yes, because the best ways of presenting data appear by themselves during the optimization of multilayer models.
Deep learning is a very young area where theories have not yet settled down and where attitudes are changing rapidly. With this reservation, I’ll say that, it seems to me, the training of representations using neural networks is now very popular.
This post talks about many research results that seem impressive to me, but my main goal is to set the stage for the next post, which will examine the links between deep learning, type theory, and functional programming. If you're interested, in order not to miss it, you can subscribe to my RSS feed.
Further, the author asks to report any noticed inaccuracies in the comments, see the original article .
Thanks to Eliana Lorch, Yoshua Bengio, Michael Nielsen, Laura Ball, Rob Gilson and Jacob Steinhardt for comments and support.
From a translator: thank you for valuable comments by Denis Kiryanov and Vadim Lebedev.
In recent years, methods using deep neural networks have taken a leading position in pattern recognition. Thanks to them, the bar for the quality of computer vision methods has risen significantly. Speech recognition is moving in the same direction.
Results are results, but why do they solve problems so cool?
The post highlights some of the impressive results of using deep neural networks in Natural Language Processing (NLP). Thus, I hope to lucidly state one of the answers to the question why deep neural networks work .
Hidden Layer Neural Networks
A neural network with a hidden layer is universal: with a sufficiently large number of hidden nodes, it can build an approximation of any function. There is a frequently quoted (and even more often incorrectly understood and applied) theorem about this.
This is true because the hidden layer can simply be used as a “lookup table".
For simplicity, consider the perceptron. This is a very simple neuron that fires if its value exceeds a threshold value, and does not fire if not. The perceptron has binary inputs and a binary output (i.e. 0 or 1). The number of input value options is limited. Each of them can be associated with a neuron in a hidden layer that works only for a given input.
Analysis of the “condition” for each individual input will require
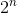hidden neurons (for ndata). In fact, usually it’s not so bad. There may be “conditions” under which several input values are suitable, and there may be “overlapping” “conditions” that reach the correct inputs at their intersection. Then we can use the connections between this neuron and the output neurons to set the final value for this particular case.
Universality is possessed not only by perceptrons. Networks with sigmoid cells in neurons (and other activation functions) are also universal: with a sufficient number of hidden neurons, they can build an arbitrarily accurate approximation of any continuous function. It is much more difficult to demonstrate this, since you cannot just take and isolate the inputs from each other.
Therefore, it turns out that neural networks with one hidden layer are actually universal. However, this is not impressive or surprising. The fact that the model can work as a look-up table is not the strongest argument in favor of neural networks. This just means that the model is basically capable of coping with the task. By universality we mean only that the network can adapt to any samples, but this does not mean that it is able to adequately interpolate the solution for working with new data.
No, versatility does not yet explain why neural networks work so well. The correct answer lies a little deeper. To understand, we first consider a few specific results.
Vector representations of words (word embeddings)
I'll start with a particularly interesting sub-area of deep learning - with vector representations of words (word embeddings). In my opinion, vector representations are now one of the coolest topics for research in deep learning, although they were first proposed by Bengio, et al. more than 10 years ago.
Vector representations were first proposed by Bengio et al, 2001 and Bengio et al, 2003 several years before the resurrection of deep learning in 2006, when neural networks were not yet in fashion. The idea of distributed representations as such is even older (see, for example, Hinton 1986 ).
In addition, I think that this is one of those tasks with which the best way to form an intuitive understanding of why deep learning is so effective.
A vector representation of a word
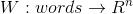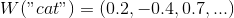
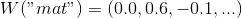
is a parameterized function that maps words from a certain natural language to large-dimension vectors (say, from 200 to 500 dimensions). For example, it may look like this: (As a rule, this function is defined by a lookup table defined by a matrix
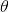in which each word corresponds to a row 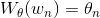). W is initialized with random vectors for each word. She will be trained to give meaningful values to solve a problem.
For example, we can drag the network to determine if the 5-gram is “correct” (a five-word sequence, for example, 'cat sat on the mat'). 5 grams can be easily obtained from Wikipedia, and then half of them are “spoiled”, replacing each of some of the words with a random one (for example, 'cat sat song the mat'), since this almost always makes the 5 gram meaningless .
A modular network to determine if a 5-gram is “correct” ( Bottou (2011) ).
The model that we train will pass each 5-gram word through W , receiving their vector representations at the output, and feed them to another module, R , which will try to predict whether the 5-gram is “correct” or not. We want it to be this way:
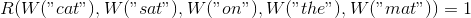
In order to predict these values accurately, the network needs to select parameters for W and R well .
However, this task is boring. Probably, the solution found will help to find grammatical errors in the texts or something like that. But what's really valuable, since it obtained the W .
(In fact, all the salt of the assignment in trainingThe W . We could consider solutions to other problems; so, one of the most common is the prediction of the next word in a sentence. But this is not our goal now. In the remainder of this section, we will talk about many of the results of the vector representation of words and will not be distracted by highlighting the difference between the approaches).
To "feel" how the space of vector representations is arranged, you can depict them using the tricky method of visualizing high-dimensional data - tSNE.
Visualization of vector representations of words using tSNE. On the left is the “area of numbers”, on the right is the “area of professions” (from Turian et al. (2010) ).
Such a “word map” seems quite meaningful. “Similar” words are close, and if you look at which ideas are closer to the others, it turns out that at the same time, close ones are “similar”.
Whose vector representations are closer to the representation of a given word? ( Collobert et al. (2011) .)
It seems natural that a network matches words with similar meanings to close vectors. If you replace the word with a synonym (“some sing well”,
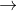“few sing well”), then the “correctness” of the sentence does not change. It would seem that the input sentences differ significantly, but since W “shifts” the representations of synonyms (“some” and “few”) to each other, little changes for R.This is a powerful tool. The number of possible 5 grams is huge, while the size of the training sample is relatively small. The convergence of representations of similar words allows us, taking one sentence, how to work with a whole class of "similar" ones. The case is not limited to replacing synonyms, for example, it is possible to substitute a word from the same class (“wall blue”
“wall red”). Moreover, it makes sense to replace several words at the same time (“blue wall”, “red ceiling”). The number of such “similar phrases” is growing exponentially from the number of words. Already in the fundamental work of A Neural Probabilistic Language Model (Bengio, et al. 2003), substantial explanations are given why vector representations are such a powerful tool.
Obviously, this property is Wwould be very helpful. But how is she taught? It is very likely that many times W encounters the sentence “wall blue” and recognizes it as correct before seeing the sentence “wall red”. Shifting “red” closer to “blue” improves network performance.
We still need to deal with examples of uses of each word, but analogies allow us to generalize to new combinations of words. With all the words whose meaning we understand, we have come across before, but the meaning of the sentence can be understood without ever hearing it before. Neural networks can do the same.
Mikolov et al. (2013a)
Vector representations have another much more remarkable property: it seems that the analogy relations between words are determined by the value of the difference vector between their representations. For example, judging by everything, the difference vector of “male-female” words is constant:
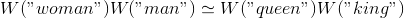
Maybe it won’t surprise anyone. In the end, the presence of pronouns of the genus suggests that replacing the word "kills" the grammatical correctness of the sentence. We write: “she is an aunt,” but “he is an uncle.” Similarly, "he is the king" and "she is the queen." If we see in the text “she is uncle”, most likely this is a grammatical error. If in half the cases the words were replaced randomly, then this must be our case.
"Of course!" - we say, looking back at past experience. “Vector representations will be able to represent gender. Surely there is a separate dimension for the floor. And also for the plural / singular. Yes, such relationships are easily recognized! ”
It turns out, however, that much more complex relationships are “coded” similarly. Just miracles in the sieve (well, almost)!
Relationship Pairs (from Mikolov et al. (2013b) .)
It is important that all of these W properties are side effects. We did not impose requirements that representations of similar words should be close to each other. We did not try to adjust the analogies ourselves with the help of vector differences. We just tried to learn how to check whether the proposal is “correct”, and the properties came from somewhere in the process of solving the optimization problem.
The great strength of neural networks seems to be that they automatically learn to build the “best” representations of the data. In turn, data presentation is an essential part of solving many machine learning problems. And vector representations of words is one of the most amazing examples of learning a representation.
Shared representations
The properties of vector representations are, of course, curious, but can we do something useful with their help? In addition to stupid little things like checking if a particular 5-gram is “correct”.
W and F train, driving task under A . Then G will be able to learn to solve the problem of Bed and , using the W .
We trained vector representations of words in order to cope with simple tasks well, but knowing their wonderful properties that we have already observed, we can assume that they will be useful for more general problems. In fact, vector representations like these are terribly important:
"The use of vector representations of words ... has recently become the main" secret of the company "in many natural language processing systems, including the tasks of distinguishing named entities (named entity recognition), part-of-speech tagging, parsing and definitions of semantic roles (semantic role labeling). "
( Luong et al. (2013) .)
The general strategy is to train a good representation for Problem A and use it to solve Problem B - one of the main tricks in the deep learning magic hat. In different cases, it is called differently: pretraining, transfer learning, and multi-task learning. One of the strengths of this approach is that it allows you to train presentations on several types of data.
You can crank up this trick in a different way. Instead of adjusting the views for one data type and using them to solve problems of different types, you can display different types of data in a single view!
One of the great examples of using this trick is the vector representation of words for two languages proposed by Socher et al. (2013a) . We can learn to “embed” words from two languages into a single space. In this work, words from the English language and Putonghua (“Mandarin dialect” of Chinese) are “embedded”.
We train two vector representations
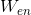and 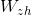in the same way as we did above. However, we know that some words in English and Chinese have similar meanings. So, we will optimize by one more criterion: the representations of the translations we know should be at a small distance from each other. Of course, in the end we observe that the “similar” words known to us are stacked side by side. No wonder, because we have optimized so. What is much more interesting is this: translations that we did not know about are also nearby.
Perhaps this no longer surprises anyone in the light of our past experience with vector representations of words. They “attract” similar words to each other, therefore, if we know that English and Chinese words mean approximately the same thing, then the representations of their synonyms should be nearby. We also know that pairs of words in relationships like differences in gender (gender) differ by a constant vector. It seems that if you “pull together” a sufficient number of translations, you will be able to adjust the differences so that they are the same in two languages. As a result, if the "male versions" of the word in both languages are translated into each other, we automatically get that the "female versions" are also correctly translated.
Intuition suggests that languages must have a similar “structure” and that by forcibly linking them at the selected points, we pull up the rest of the ideas in the right places.
Visualization of bilingual vector representations using t-SNE. Chinese is highlighted in green, English is marked in yellow ( Socher et al. (2013a) ).
When dealing with two languages, we teach a common representation for two similar data types. But we can "fit" into a single space and very different types of data.
Recently, with the help of deep learning, they began to build models that “fit” images and words into a single space of representations.
In a previous work, we simulated the joint distribution of labels and images, but here it’s a bit different.
The main idea is that we classify images by issuing a vector from the space of word representations. Pictures with dogs are displayed in vectors near the representation of the word “dog”, with horses - about “horse”, with a car - about “car”. Etc.
The most interesting thing happens when you test a model on new image classes. So what will happen if we propose to classify the image of a cat seal of a model that was not taught to specifically recognize them, that is, to display it in a vector close to the “cat” vector?
Socher et al. (2013b)
It turns out that the network does a good job with new image classes. Images of cats are not displayed at random points in space. On the contrary, they fit in the vicinity of the "dog" vector and are pretty close to the "cat" vector. Similarly, truck images are displayed at points close to the “truck” vector, which is not far from the associated “car” vector.
Socher et al. (2013b)
Stanford group members did this with 8 known classes and two unknowns. The results are already impressive. But with such a small number of classes, there are not enough points on which the relationship between images and semantic space can be interpolated.
The Google research team has built a much larger version of the same; they took 1,000 categories instead of 8 - and at about the same time ( Frome et al. (2013) ), and then suggested another option ( Norouzi et al. (2014) ). The last two works are based on a strong model for classifying images ( Krizehvsky et al. (2012) ), but the images in them fit into the space of vector representations of words in different ways.
And the results are impressive. If it is not possible to accurately map the images of unknown classes to the correct vector, then at least it is possible to get into the right neighborhood. Therefore, if you try to classify images from unknown and significantly different categories, then at least classes can be distinguished.
Even if I have never seen a Aesculapian snake or an armadillo when their pictures are shown to me, I can tell who is shown where, because I have a general idea of what kind of appearance these animals can have. And such networks are also capable of this.
(We often used the phrase “these words are similar.” But it seems that much stronger results can be obtained based on the relationship between words. In our space of word representations, there is a constant difference between the “male” and “female versions.” But also in space Representations of images have reproducible properties that allow you to see the difference between the sexes.The beard, mustache and bald head are clearly recognizable signs of a man.Chest and long hair (a less reliable sign), makeup and jewelry are obvious indicators female I am well aware that the physical signs of the floor are deceptive, for example, I'm not going to say that all the bald -. men, or that all who have a bust - a woman, but that it is more likely true than not, help. we better set the initial values.
. Even if you have never seen a king, then when you see a queen (which you identified by the crown) with a beard, you will probably decide that you need to use the “masculine version” of the word “queen”).
General views (shared embeddings) - a breathtaking field of research; they are a very convincing argument in favor of promoting the training of ideas on the fronts of deep learning.
Recursive Neural Networks
We started the discussion of vector representations of words with such a network:
A Modular Network that teaches vector representations of words ( Bottou (2011) ).
The diagram shows a modular network
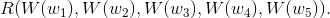
It is constructed from two modules, W and R . This approach to building neural networks - from smaller "neural network modules" - is not too widespread. However, he showed himself very well in the tasks of processing natural language.
The models that were described are strong, but they have one annoying limitation: the number of inputs they cannot change.
This can be dealt with by adding the associative module A , which “merges” the two vector representations.
From Bottou (2011)
“Merging” word sequences, A allows you to represent phrases and even whole sentences. And since we want to "merge" a different number of words, the number of inputs should not be limited.
It is not a fact that it is correct to “merge” words in a sentence simply in order. The sentence 'the cat sat on the mat' can be decomposed into parts like this: '((the cat) (sat (on (the mat))'. We can apply A using this arrangement of brackets:
From Bottou (2011)
These models are often called recursive neural networks, since the output signal of one module is often fed to another module of the same type. Sometimes they are also called neural networks of a tree structure (tree-structured neural networks).
Recursive neural networks have achieved significant success in solving several problems of natural language processing. For example, in Socher et al. (2013c) they are used to predict sentiment sentence:
(From Socher et al. (2013c) .) The
main goal is to create a “reversible” representation of the proposal, that is, such that it can be reconstructed from the proposal with approximately the same value. For example, you can try to introduce a dissociative module D , which will perform the opposite action of A :
From Bottou (2011)
If it succeeds, then we will have an incredibly powerful tool on hand. For example, you can try to build proposal views for two languages and use it for automatic translation.
Unfortunately, it turns out to be very difficult. Terribly difficult. But, having received the basis for hope, many are struggling to solve the problem.
Recently, Cho et al. (2014) , progress has been made in the presentation of phrases, with a model that “encodes” a phrase in English and “decodes” it as a phrase in French. Just look what kind of performance comes out!
A small piece of representation space compressed with tSNE ( Cho et al. (2014) .)
Criticism
I heard that some of the results discussed above were criticized by researchers from other areas, in particular, linguists and natural language processing specialists. It is not the results themselves that are criticized, but the consequences that are deduced from them, and the methods of comparison with other approaches.
I don’t think that I’m prepared so well to articulate exactly what the problem is. I would be glad if someone did this in the comments.
Conclusion
Deep learning in the service of learning representations is a powerful approach that seems to answer the question of why neural networks are so efficient. In addition, it has amazing beauty: why are neural networks effective? Yes, because the best ways of presenting data appear by themselves during the optimization of multilayer models.
Deep learning is a very young area where theories have not yet settled down and where attitudes are changing rapidly. With this reservation, I’ll say that, it seems to me, the training of representations using neural networks is now very popular.
This post talks about many research results that seem impressive to me, but my main goal is to set the stage for the next post, which will examine the links between deep learning, type theory, and functional programming. If you're interested, in order not to miss it, you can subscribe to my RSS feed.
Further, the author asks to report any noticed inaccuracies in the comments, see the original article .
Acknowledgments
Thanks to Eliana Lorch, Yoshua Bengio, Michael Nielsen, Laura Ball, Rob Gilson and Jacob Steinhardt for comments and support.
From a translator: thank you for valuable comments by Denis Kiryanov and Vadim Lebedev.