Sound Fingerprints: Recognizing Radio Ads
From this article you will learn that recognition of even short sound fragments in a noisy recording is a completely solvable task, and the prototype is generally implemented in 30 lines of Python code. We will see how the Fourier transform helps here, and visually see how the algorithm for searching and matching fingerprints works. The article will be useful if you yourself want to write a similar system, or you are interested in how it can be arranged.
To begin with, we ask ourselves: who generally needs to recognize ads on the radio? This is useful for advertisers who can track the actual outputs of their commercials, catch cases of trimming or interruption; radio stations can monitor the output of network advertising in regions, etc. The same recognition problem arises if we want to track the playback of a musical work (which the copyright holders really like), or to learn a song from a small fragment (like Shazam and other similar services do).
The task is formulated more strictly as follows: we have a certain set of reference audio fragments (songs or commercials), and there is an audio recording of the ether in which some of these fragments are supposedly sound. The task is to find all the fragments that have sounded, to determine the moments of the beginning and the duration of playback. If we analyze airtime recordings, then the whole system needs to be faster than real time.
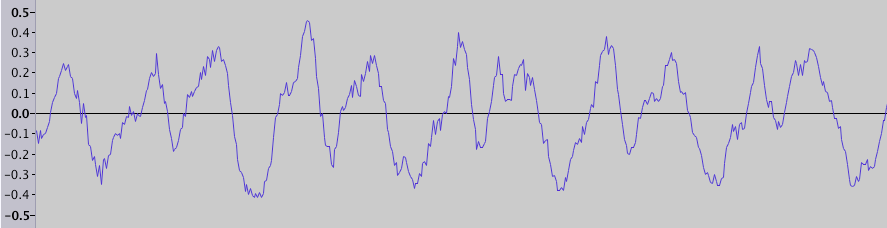
Everyone knows that sound (in the narrow sense) is a wave of compression and rarefaction propagating in the air. Sound recording, for example in a wav file, is a sequence of amplitude values (physically it corresponds to the compression ratio, or pressure). If you opened the audio editor, you probably saw a visualization of this data - a graph of the amplitude versus time (fragment duration 0.025 s):
But we do not perceive these frequency fluctuations directly, but we hear sounds of different frequencies and timbres. Therefore, another way of sound visualization is often used - a spectrogram , where time is represented on the horizontal axis, frequency is shown on the vertical axis, and the color of the dot indicates amplitude. For example, here is a spectrogram of the sound of a violin spanning several seconds in time:
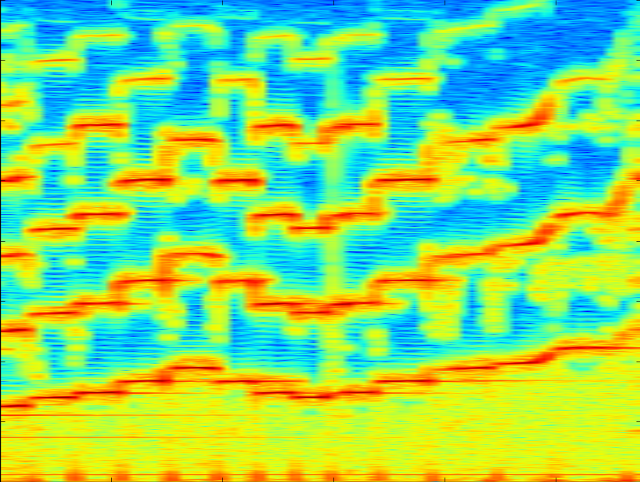
It shows individual notes and their harmonics, as well as noise - vertical stripes covering the entire frequency range.
The task of searching for a fragment on the air can be divided into two parts: first, find candidates among a large number of reference fragments, and then check whether the candidate really sounds in this fragment of the air, and if so, at what point does the sound begin and end. Both operations use the “imprint” of the sound fragment for their work. It should be noise resistant and compact enough. This imprint is constructed as follows: we divide the spectrogram into short periods of time, and in each such segment we look for the frequency with the maximum amplitude (in fact, it is better to look for several maxima in different ranges, but for simplicity we take one maximum in the most meaningful range). The set of such frequencies (or frequency indices) is an imprint. It is very rude to say that these are “notes” that sound at every moment in time.
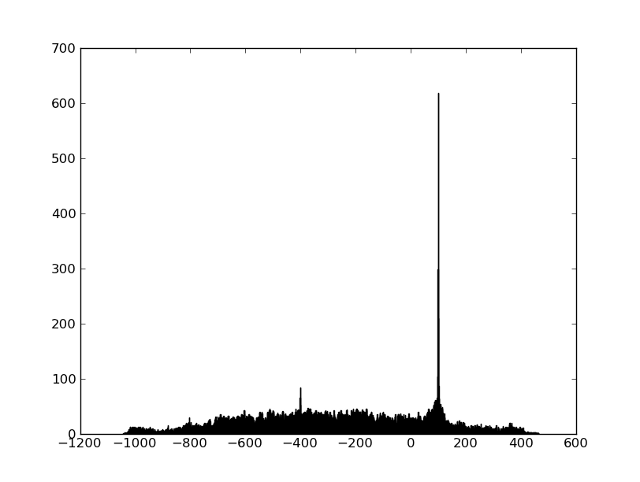
We can get the imprint of the ether fragment and all the reference fragments, and we just need to learn how to quickly search for candidates and compare fragments. First, let's look at the comparison problem. It is clear that prints will never match exactly due to noise and distortion. But it turns out that the frequencies so coarsened in this way survive all distortions quite well (the frequencies almost never “float”), and a sufficiently large percentage of frequencies coincides exactly - so we can only find a shift at which there are many coincidences among the two frequency sequences. A simple way to visualize this is to first find all pairs of points that coincide in frequency, and then build a histogram of the time differences between the coincident points. If two fragments have a common area,
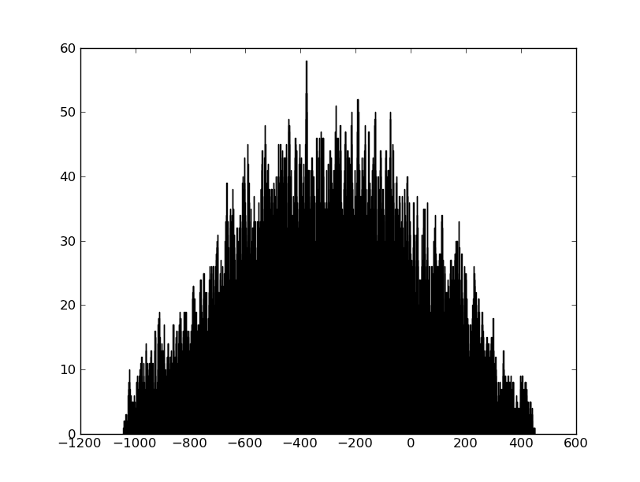
If the two fragments are not connected in any way, then there will be no peak:
The problem of searching for candidates is usually solved using hashing - the number of hashes is constructed from the fingerprint of the fragment, as a rule these are several values from the fingerprint going in a row or at some distance. The different approaches can be viewed at the links at the end of the article. In our case, the number of reference fragments was of the order of hundreds, and it was possible to do without the stage of selecting candidates.
On those records that we had, the F-score was 98.5%, and the accuracy of determining the beginning was about 1 s. As expected, most of the errors were on short (4-5 s) clips. But the main conclusion for me personally is that in such problems a solution written independently often works better than a ready-made one (for example, from EchoPrint, which we already wrote about in the Habré, it was possible to squeeze no more than 50-70% due to short clips) simply because that all tasks and data have their own specifics, and when there are a lot of variations in the algorithm and a great arbitrariness in the choice of parameters, then understanding of all stages of work and visualization on real data greatly contributes to a good result.
Fun facts:
Literature:
To begin with, we ask ourselves: who generally needs to recognize ads on the radio? This is useful for advertisers who can track the actual outputs of their commercials, catch cases of trimming or interruption; radio stations can monitor the output of network advertising in regions, etc. The same recognition problem arises if we want to track the playback of a musical work (which the copyright holders really like), or to learn a song from a small fragment (like Shazam and other similar services do).
The task is formulated more strictly as follows: we have a certain set of reference audio fragments (songs or commercials), and there is an audio recording of the ether in which some of these fragments are supposedly sound. The task is to find all the fragments that have sounded, to determine the moments of the beginning and the duration of playback. If we analyze airtime recordings, then the whole system needs to be faster than real time.
How it works
Everyone knows that sound (in the narrow sense) is a wave of compression and rarefaction propagating in the air. Sound recording, for example in a wav file, is a sequence of amplitude values (physically it corresponds to the compression ratio, or pressure). If you opened the audio editor, you probably saw a visualization of this data - a graph of the amplitude versus time (fragment duration 0.025 s):

But we do not perceive these frequency fluctuations directly, but we hear sounds of different frequencies and timbres. Therefore, another way of sound visualization is often used - a spectrogram , where time is represented on the horizontal axis, frequency is shown on the vertical axis, and the color of the dot indicates amplitude. For example, here is a spectrogram of the sound of a violin spanning several seconds in time:

It shows individual notes and their harmonics, as well as noise - vertical stripes covering the entire frequency range.
To build such a spectrogram using Python, you can do this:
To load data from a wav file, you can use the SciPy library , and to build a spectrogram use matplotlib . All examples are given for Python version 2.7, but should probably work for version 3. We assume that file.wav contains a sound recording with a sampling frequency of 8000 Hz:
import numpy
from matplotlib import pyplot, mlab
import scipy.io.wavfile
from collections import defaultdict
SAMPLE_RATE = 8000 # Hz
WINDOW_SIZE = 2048 # размер окна, в котором делается fft
WINDOW_STEP = 512 # шаг окна
def get_wave_data(wave_filename):
sample_rate, wave_data = scipy.io.wavfile.read(wave_filename)
assert sample_rate == SAMPLE_RATE, sample_rate
if isinstance(wave_data[0], numpy.ndarray): # стерео
wave_data = wave_data.mean(1)
return wave_data
def show_specgram(wave_data):
fig = pyplot.figure()
ax = fig.add_axes((0.1, 0.1, 0.8, 0.8))
ax.specgram(wave_data,
NFFT=WINDOW_SIZE, noverlap=WINDOW_SIZE - WINDOW_STEP, Fs=SAMPLE_RATE)
pyplot.show()
wave_data = get_wave_data('file.wav')
show_specgram(wave_data)
The task of searching for a fragment on the air can be divided into two parts: first, find candidates among a large number of reference fragments, and then check whether the candidate really sounds in this fragment of the air, and if so, at what point does the sound begin and end. Both operations use the “imprint” of the sound fragment for their work. It should be noise resistant and compact enough. This imprint is constructed as follows: we divide the spectrogram into short periods of time, and in each such segment we look for the frequency with the maximum amplitude (in fact, it is better to look for several maxima in different ranges, but for simplicity we take one maximum in the most meaningful range). The set of such frequencies (or frequency indices) is an imprint. It is very rude to say that these are “notes” that sound at every moment in time.
Here's how to get a sound imprint
def get_fingerprint(wave_data):
# pxx[freq_idx][t] - мощность сигнала
pxx, _, _ = mlab.specgram(wave_data,
NFFT=WINDOW_SIZE, noverlap=WINDOW_OVERLAP, Fs=SAMPLE_RATE)
band = pxx[15:250] # наиболее интересные частоты от 60 до 1000 Hz
return numpy.argmax(band.transpose(), 1) # max в каждый момент времени
print get_fingerprint(wave_data)
We can get the imprint of the ether fragment and all the reference fragments, and we just need to learn how to quickly search for candidates and compare fragments. First, let's look at the comparison problem. It is clear that prints will never match exactly due to noise and distortion. But it turns out that the frequencies so coarsened in this way survive all distortions quite well (the frequencies almost never “float”), and a sufficiently large percentage of frequencies coincides exactly - so we can only find a shift at which there are many coincidences among the two frequency sequences. A simple way to visualize this is to first find all pairs of points that coincide in frequency, and then build a histogram of the time differences between the coincident points. If two fragments have a common area,

If the two fragments are not connected in any way, then there will be no peak:

You can build such a wonderful histogram like this:
Files on which you can practice recognition work here .
def compare_fingerprints(base_fp, fp):
base_fp_hash = defaultdict(list)
for time_index, freq_index in enumerate(base_fp):
base_fp_hash[freq_index].append(time_index)
matches = [t - time_index # разницы времен совпавших частот
for time_index, freq_index in enumerate(fp)
for t in base_fp_hash[freq_index]]
pyplot.clf()
pyplot.hist(matches, 1000)
pyplot.show()
Files on which you can practice recognition work here .
The problem of searching for candidates is usually solved using hashing - the number of hashes is constructed from the fingerprint of the fragment, as a rule these are several values from the fingerprint going in a row or at some distance. The different approaches can be viewed at the links at the end of the article. In our case, the number of reference fragments was of the order of hundreds, and it was possible to do without the stage of selecting candidates.
results
On those records that we had, the F-score was 98.5%, and the accuracy of determining the beginning was about 1 s. As expected, most of the errors were on short (4-5 s) clips. But the main conclusion for me personally is that in such problems a solution written independently often works better than a ready-made one (for example, from EchoPrint, which we already wrote about in the Habré, it was possible to squeeze no more than 50-70% due to short clips) simply because that all tasks and data have their own specifics, and when there are a lot of variations in the algorithm and a great arbitrariness in the choice of parameters, then understanding of all stages of work and visualization on real data greatly contributes to a good result.
Fun facts:
- Spectrogram of one of Aphex Twin's tracks has a human face
- The author of the article, who reproduced the Shazam algorithm in Java, received threatening letters from their lawyers
Literature:
