Calculation of pre-splitter parameters for 8250-compatible USART
- Tutorial
Tonight I will tell a fairy tale on how to efficiently calculate the parameters of the splitter, which is usually used to set the clock frequency of USART ports, in particular the 8250-compatible ones used in Intel SoC.
At the moment, there are at least two lines of Intel SoC that use USART with a fractional pre-divider
What is the difference between them, I will tell a little later.
Below are the formulas used to calculate Fusart - USART clock frequency, and baud - baud rate.
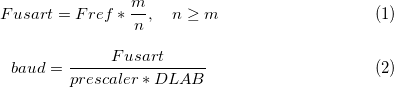
The remaining
Frefs are the frequency before the pre-divider, m is the numerator, n is the denominator of the rational fraction of the pre-divider, prescaler is the integer by which Fusart is divided , DLAB is the 16-bit divider, presented in 8250-compatible chips.
From the whole set, we know only two quantities, namely: Fref and baud . The value of prescaler is usually equal to 16 and in some chips there is no possibility to change it (this is what distinguishes the Intel SoC line from each other)
Since we are working with a fractional prescaler, and not with a full-fledged PLL, it follows from (1)

And therefore, we can already calculate the prescaler value
The previous part only works if it is not satisfied (3) . Otherwise, Fusart may turn out to be very low relative to Fref at the requested rather low bit rate, for example 110 baud.
And since the numerator and denominator of the divider are usually of equal width (in bits), it would be nice to limit their discrepancy. To do this, bring Fusart to Fref as far as possible.
Why is this approximation chosen? The thing is, if we have DLAB overflow , and it is only 16-bit, then if we use the power of two, we can track this with the simplest bit operations.
Obviously, now from (1,2) , a simple proportion follows

Thus, we easily calculate the numerator and denominator of the rational fraction of the pre-divisor.
Here width is the width in bits of the numerator and denominator.
That's all. For those who wish, the source code for Python can be found on the GitHub Gist (it has already been updated several times and may be updated in the future).
Please note that the above algorithm is simple and fast, although not so accurate, but it satisfies our goal.
At the moment, there are at least two lines of Intel SoC that use USART with a fractional pre-divider
- Medfield, CloverTrail, Tangier
- BayTrail, Braswell
What is the difference between them, I will tell a little later.
Below are the formulas used to calculate Fusart - USART clock frequency, and baud - baud rate.
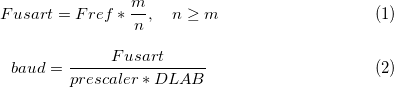
The remaining
Frefs are the frequency before the pre-divider, m is the numerator, n is the denominator of the rational fraction of the pre-divider, prescaler is the integer by which Fusart is divided , DLAB is the 16-bit divider, presented in 8250-compatible chips.
From the whole set, we know only two quantities, namely: Fref and baud . The value of prescaler is usually equal to 16 and in some chips there is no possibility to change it (this is what distinguishes the Intel SoC line from each other)
Calculation of prescaler
Since we are working with a fractional prescaler, and not with a full-fledged PLL, it follows from (1)

And therefore, we can already calculate the prescaler value
prescaler = 16
fusart = baud * prescaler
if fref < fusart:
if fref >= baud:
prescaler = fref / baud
else:
prescaler = 1
fusart = baud * prescaler
Fusart Calculation
The previous part only works if it is not satisfied (3) . Otherwise, Fusart may turn out to be very low relative to Fref at the requested rather low bit rate, for example 110 baud.
And since the numerator and denominator of the divider are usually of equal width (in bits), it would be nice to limit their discrepancy. To do this, bring Fusart to Fref as far as possible.
fusart <<= int(math.log(fref / fusart, 2))
Why is this approximation chosen? The thing is, if we have DLAB overflow , and it is only 16-bit, then if we use the power of two, we can track this with the simplest bit operations.
Denominator Queue
Obviously, now from (1,2) , a simple proportion follows

Thus, we easily calculate the numerator and denominator of the rational fraction of the pre-divisor.
divisor = gcd(fref, fusart)
n = fref / divisor
while n > (2 ** width - 1):
divisor <<= 1
n >>= 1
m = fusart / divisor
Here width is the width in bits of the numerator and denominator.
That's all. For those who wish, the source code for Python can be found on the GitHub Gist (it has already been updated several times and may be updated in the future).
Calculation example for Fref = 50MHz, width = 24 bits
Вывод в формате 1) m, 2) n, 3) prescaler, 4) Fusart, 5) загадочное число, 6) список скоростей передачи, в скобках значение DLAB.
24 25 12 48000000 64000000 4000000(1)
49 50 14 49000000 56000000 3500000(1)
4 5 16 40000000 40000000 2500000(1)
16 25 16 32000000 32000000 500000(4),1000000(2),2000000(1)
24 25 16 48000000 48000000 1500000(2),3000000(1)
2304 3125 16 36864000 36864000 576000(4),1152000(2)
8192 15625 16 26214400 26214400 50(32768),200(8192)
9216 15625 16 29491200 29491200 1800(1024),57600(32),115200(16),230400(8),460800(4),921600(2),1843200(1)
12288 15625 16 39321600 39321600 75(32768),150(16384),300(8192),600(4096),1200(2048),2400(1024),4800(512),9600(256),19200(128),38400(64)
45056 78125 16 28835840 28835840 110(16384)
274432 390625 16 35127296 35127296 134(16384)
24 25 12 48000000 64000000 4000000(1)
49 50 14 49000000 56000000 3500000(1)
4 5 16 40000000 40000000 2500000(1)
16 25 16 32000000 32000000 500000(4),1000000(2),2000000(1)
24 25 16 48000000 48000000 1500000(2),3000000(1)
2304 3125 16 36864000 36864000 576000(4),1152000(2)
8192 15625 16 26214400 26214400 50(32768),200(8192)
9216 15625 16 29491200 29491200 1800(1024),57600(32),115200(16),230400(8),460800(4),921600(2),1843200(1)
12288 15625 16 39321600 39321600 75(32768),150(16384),300(8192),600(4096),1200(2048),2400(1024),4800(512),9600(256),19200(128),38400(64)
45056 78125 16 28835840 28835840 110(16384)
274432 390625 16 35127296 35127296 134(16384)
Please note that the above algorithm is simple and fast, although not so accurate, but it satisfies our goal.
