Fragmented compression method of a video stream
I decided to submit my development to the court of the respected habrasociety - the method of fragmentary compression of the video stream. A feature of the proposed method is the complete correspondence of the compressed video stream to the original, that is, the method performs lossless compression.
Before describing the method itself, it is necessary to agree on the terminology used. All the terms used are intuitive, but nevertheless, it is worth defining them strictly:
The main idea of the fragmented compression method is to represent the video stream in the form of a chain of elements of length N f from the base of elements. Since the video stream is a set of meaningful images (frames) that change quite slowly over time, a significant correlation should be expected both between neighboring elements of one frame and between the corresponding elements in neighboring frames. This should lead to two effects:
Thus, the main idea of the method of fragmentary compression is to represent the video stream in the form of a well-compressible sequence of elements from some specially composed base of elements. The experiments conducted by the authors confirm this hypothesis.
The concept of the method allows compressing the video stream both without losses and with losses. In the case of lossy compression, both pre-processing (filtering) is possible, which makes it possible to smooth the original image, and post-processing, which consists in analyzing the base of elements and then extracting and removing from the video stream both random noise and visually redundant information. The joint use of pre- and post-processing allows you to create a new compressed video stream with the desired properties.
The method of fragmentary compression can be represented as a sequence of four steps:
These steps are discussed in more detail below.
The process of forming the base of elements is one of the most resource-intensive steps of the fragmented compression method. The final compression rate largely depends on how efficiently this step is performed.
Due to the extremely high requirements for speed, the algorithm for forming the base of elements is performed in several stages, with different algorithms and data structures being used at each step.
Formation of the base of frame elements is the first and easiest step. At this stage, the next frame is received from the video stream, its preliminary processing if necessary, and, depending on the type of element, the corresponding “pseudo-frame” is formed.
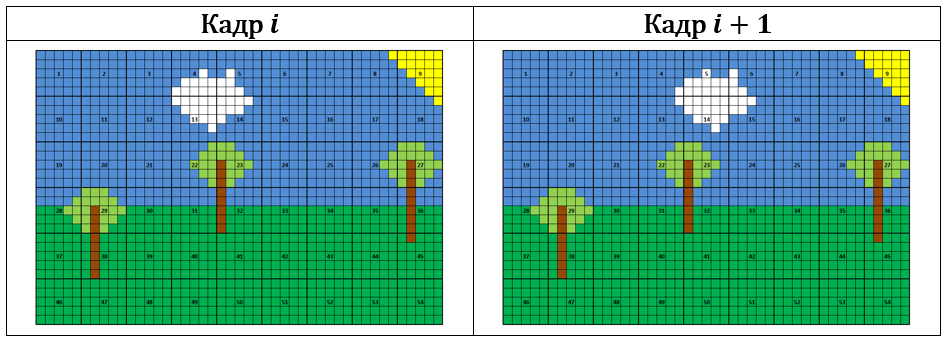
When viewing a pseudo-frame, the window is shifted n 2 pixels wide and n 1pixels in height. The figure shows an example of a frame N 1 = 30 rows by N 2 = 45 columns, viewing is performed using the square window n 1 = n 2 = 5. Thin lines in the figure highlight individual pixels, thick lines show the borders of the window, and the numbers inside the window show the serial number when viewing.
If the elements are logical or arithmetic differences, then the scan will result in the following set of differences:
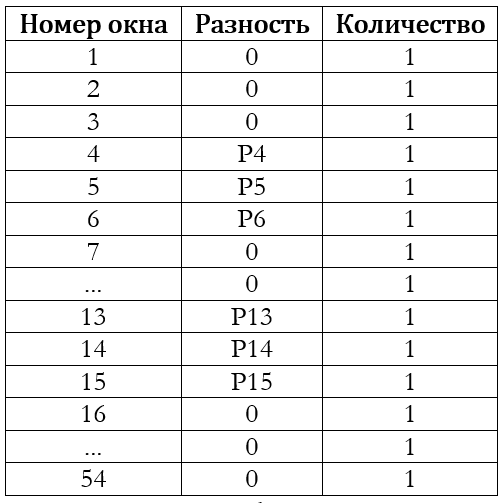
For most real videos, the assumption is made that there is a significant correlation between the corresponding elements in adjacent frames. This is also evident in the table: most elements correspond to zero differences. To save memory, the resulting frame element base is compacted. First, sorting is done by some effective algorithm, and then matching elements are combined into one record. That is, instead of 48 zero differences in the compacted base there will be only one record.
At the second stage, the compressed base of the frame elements is recorded in a special buffer of elements - a separate memory area where many frame bases are accumulated, and then are written to the global storage in one large block. A feature of the buffer is that any element of it can be randomly accessed by index, i.e. in fact, it’s just a large array of elements located in RAM:
It is also worth noting that the frame element bases are written to the buffer “as is” without any additional sorting. This leads to the fact that the buffer contains a lot of ordered sequences of elements, but it is not ordered itself:

When there is not enough space to write the next frame base in the buffer, the procedure for updating the list of elements that have actually met is called.
At the third stage, the elements accumulated in the buffer are moved to a special global storage, which is a singly connected list of elements sorted by their values. Representation of the global storage in the form of a list does not allow random access for constant time, but it allows you to add and remove items in constant time.
Before adding items from the buffer to the global storage, the sorting and compaction procedure of the buffer, as previously discussed, is performed. This allows you to add items in a linear time relative to the size of the list:
The three stages considered operate on data located in RAM. The final stage involves working with data stored on hard drives. In the overwhelming majority of cases, a sufficiently powerful modern computer allows you to completely assemble the base of elements in RAM, but there are situations when the size of RAM is not enough to fit the entire base there (for example, if the formation of a common base for hundreds of hours of shooting is performed). In this case, it is necessary to save the received databases to disk as the RAM runs out, and then perform the database merge procedure.
Thus, in the process of forming the base of elements, the following sequence of steps is performed:

The analysis of the base of elements involves the analysis of both the individual values of each element and the frequency characteristics of the base. This allows, firstly, to choose effective combinations of compression methods (constructing short codes and methods of their transmission), and, secondly, in the case of compression with losses, consciously reduce the base (filtering).
The base of elements includes an array of N b lines of length k bits and a table of frequencies of occurrence of these lines in the video stream (film). This information is sufficient for applying well-known methods of entropy coding (Huffman tree, arithmetic coding, etc.). The above algorithms have very high estimates of efficiency, but their real use is associated with significant implementation difficulties.
To construct short codes of elements, the authors propose and use the previously proposed method for constructing prefix codes using secant functions. In this method, short codes of the base elements are built based on the content of the lines of the elements themselves. The author has proved that the average length of such codes does not exceed the value of H b * 1,049, where H b- entropy of the element base, calculated by the frequencies of the appearance of elements in the video stream. In numerical experiments with real films, H b never exceeded 20, which means that H b * 1,049b + 1, whence it follows that the average length of the secant codes fits into the same a priori estimates of redundancy as the Shannon-Fano and Huffman codes. At the same time, encoding using secant functions is devoid of the drawbacks that arise when encoding and decoding the large-sized digital arrays by the above methods (N b ≈10 7 -10 9 ).
In a compressed video stream, elements are replaced by previously obtained short codes. When playing a compressed video stream, a decoding problem occurs. For decoding, it is necessary to have information on the correspondence of short codes and base elements. The easiest way to transmit such information is to directly transmit the element and its frequency (number of occurrences). This method involves the transfer of the base itself, as well as an additional 64 bits per element. After receiving the data, the receiving party itself must build the code tree according to a previously reported algorithm.
A method was proposed for recording and transmitting a tree, in the leaves of which the entire base of elements was recorded. In this case, the transmission volume is equal to the volume of the base plus two additional bits for each element of the base ((k + 2) * N b ).
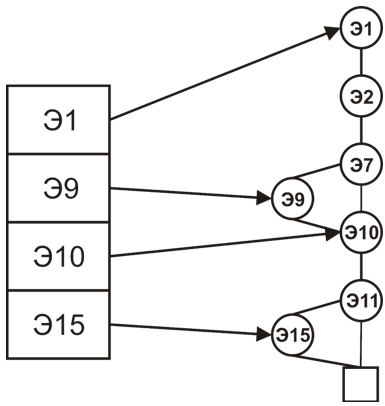
Let's agree on the tree traversal order: for example, we will use the width traversal. If a dividing tree node is found, bit 0 is transmitted, if a leaf was found during the traversal, bit 1 and the corresponding base element are transmitted. As a result, it is easy to show that only 2 extra bits are additionally transmitted to each base element. The figure shows the representation of a binary tree as a binary string using the described method:
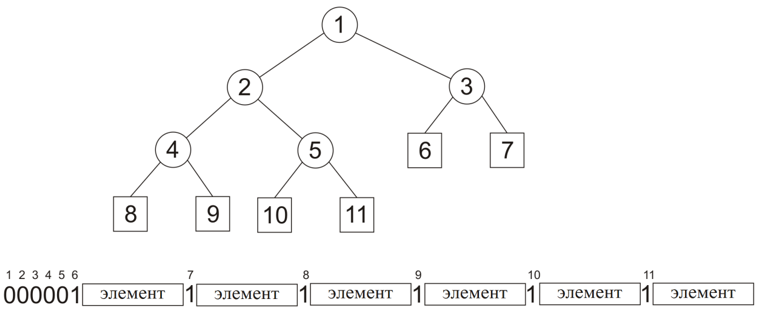
The specified representation is reversible: for each line constructed in the described way, you can build the original code tree. In addition to the obvious memory savings, the described transmission method eliminates the need to build a code tree during decoding (it is restored naturally). That is, the code tree is built only once during compression.
Thus, the paper proposes a video stream transmission scheme consisting of two parts: a code tree with base elements and a chain of compressed element codes.
An approximate structure of the compressed video stream is shown in the figure:

The compression ratio provided by the fragmented compression algorithm largely depends on the properties and characteristics of the formed base of elements. The main characteristics of the base are the size (number of elements) and frequency characteristics (primarily entropy).
To assess the achievable compression ratio, we use the following formulas. Let l sr be the average length of the base element codes, then the amount of compressed transmission is V sr = N b (k + 2) + l sr * N f , and the volume of an uncompressed film is equal to V f = N f * k.
Compression ratio value will be called:
R SJ = V SJ / V f. Contact the compression ratio value is called the compression ratio and is denoted K SJ .
The main goal to strive for is to maximize K sr . In the formula above, N 1 , N 2 , M, bpp are the characteristics of the original video stream, which we cannot influence. And the values of l cf , N of the base depend on the area and configuration of the scan window (n 1 , n 2 ). Those. the only variable parameters in the method of fragmentary compression are the geometric dimensions of the window.
For any window size, there is the maximum possible base size equal to 2 bpp * n 1 * n 2, and this value is growing extremely fast. Of course, not all possible elements are found in real films, but with an increase in the size of the window, the number of bits necessary to represent the corresponding base element also increases. In addition, a significant amount (over 70% of the total number) of elements appears that are found in the video stream no more than once. Ultimately, all of these effects lead to a decrease in compression ratio.
On the other hand, too small a window size will lead to an increase in N f and a restriction of N b , which in turn will lead to the fact that the elements will be repeated more evenly and the “distortion” of frequencies will be smoothed out. The more evenly the elements are repeated to the base, the closer its entropy is to log 2 N b. This, in turn, also leads to a decrease in compression ratio.
Consider the two extreme cases of window 1 * 1 and window N 1 * N 2 . In both the first and second cases, K cr ≈1. In the process of research, it was found that the dependence of K Comp on the area of the scan window (n 1 * n 2 ) has approximately the following form:
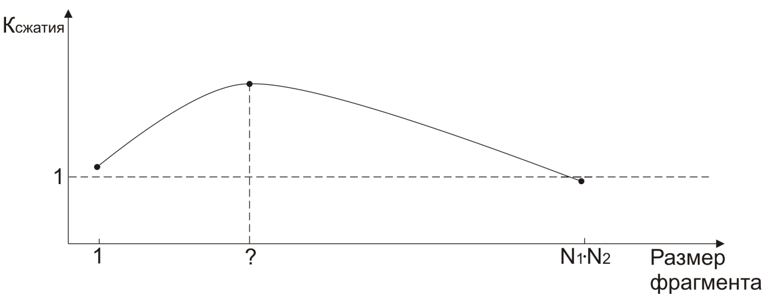
The task is to find the point where the compression level is maximum. Because the compression level also largely depends on the characteristics of the film, it is clear that there is no “ideal” configuration that will give optimal compression for all films. But experiments allowed us to find a relatively small area where compression is optimal.
All analyzed video streams were divided into two groups depending on their features:
To select the optimal window configuration, video streams belonging to each group were compressed using the fragmentary compression method. During the study, all possible window configurations with an area of one to eight pixels were analyzed (logical differences were used as elements). In total, about ten thousand hours of video were analyzed, which is about a billion frames. The results are presented in graphs.

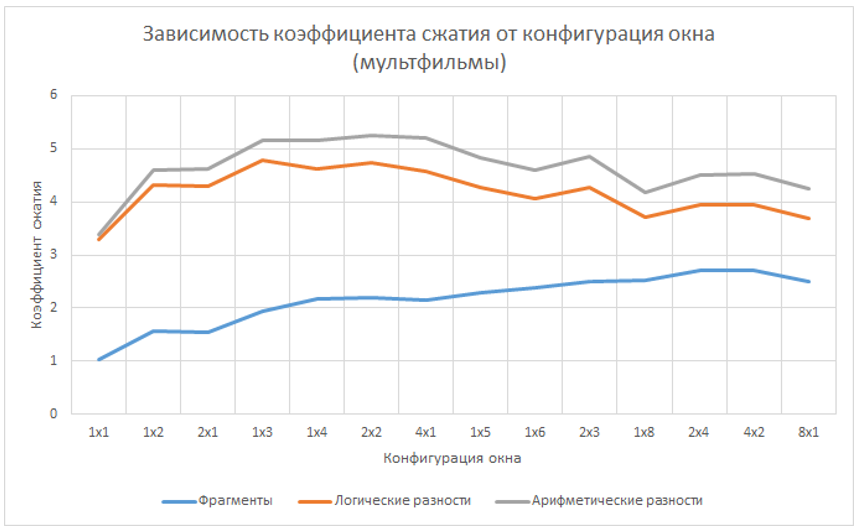
From the presented data, it is obvious that the maximum compression ratio can be achieved by using windows with an area of three, four or five pixels. Also, in the practical use of the method of fragmentary compression of the video stream, it should be taken into account that for a fixed window area, the greatest compression efficiency is observed when using a rectangular window with an aspect ratio of close to 2/1.
The previously reviewed results related to the coding of a video stream containing only the luminance component (the so-called monochrome video stream). Of great practical interest are methods that allow you to encode color video streams.
The easiest way to encode a color video stream is to independently encode color channels. A method was also considered in which element bases assembled for independent color channels were combined into one common base. Despite the fact that the share of the base in the transmission was decreasing, the increase in compression efficiency was negligible. It was also shown that the efficiency of the fragment compression method in the YIQ space is significantly higher than in the RGB space. First of all, this effect is associated with losses that occur when converting color spaces.


It is also worth noting that the compression efficiency in the YIQ space can be significantly improved due to coarse quantization of color difference channels.
Today, there are methods that allow you to compress video streams without loss. Some of them are highly specialized and effective on only one type of video stream (for example, on screen recording), other methods are effective on various video streams. This section is devoted to comparing the effectiveness of the proposed method of fragmented compression of a video stream with known methods.
In Graphics & Media Lab Video Group at Moscow State University Lomonosov made an extensive comparison of lossless video compression algorithms for a variety of parameters (compression speed, resource consumption, compression efficiency, etc.). The most important characteristic is compression efficiency. According to this criterion, the following codecs were analyzed:
Comparison was performed on standard test sequences. Each video sequence was compressed by each codec independently. The results obtained are shown in the graph:

For the convenience of analysis, the obtained values of the compression coefficients were averaged, and the obtained average estimates are given below:
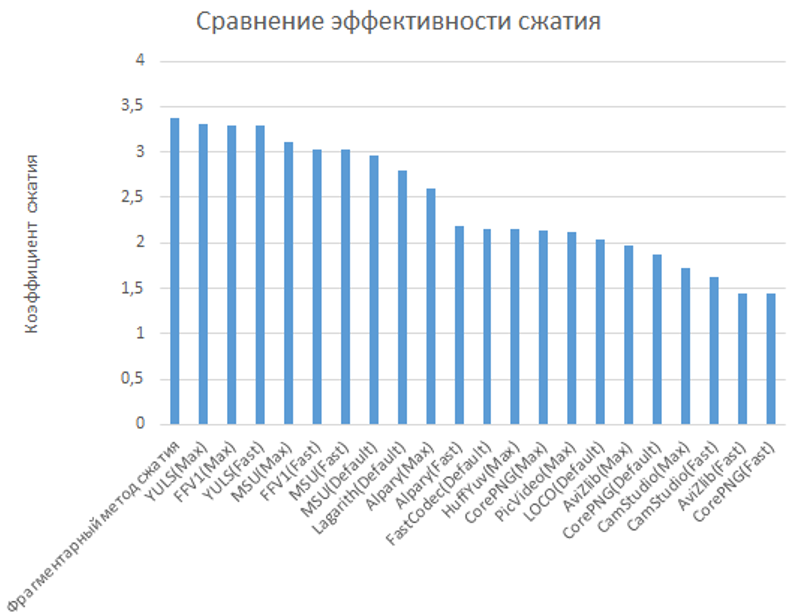
Direct application of the method of fragmentary compression on these test video sequences is ineffective. This is because the duration of the test video streams is very short and a significant part in the film compressed by the method of fragmentary compression is the element base:

With a sufficient duration of the video stream (from 5000 frames), the average compression ratio of the fragmentary compression method is 3.38, which exceeds the compression coefficients of the best of the considered methods.
If the community is interested, I will talk about the secant tree, which allowed us to achieve such a very good result.
Terminology used
Before describing the method itself, it is necessary to agree on the terminology used. All the terms used are intuitive, but nevertheless, it is worth defining them strictly:
- Pixel is the smallest unit of image. The numerical value of a pixel expresses the value of the image brightness function at one point on the screen. The number of bits allocated for encoding brightness is called the color depth and is hereinafter referred to as bpp;
- A frame is a set of all pixels at a particular moment in time. The frame is represented as a two-dimensional array of pixels with a height of N 1 and a width of N 2 pixels.
- A video stream (film) is a sequence of frames ordered by time. The total number of frames in the film is hereinafter referred to as M.
- A window is a rectangular region of pixels of height n 1 and width n 2 .
- A fragment is a part of a frame bounded by a window.
- Logical difference is the result of applying the addition operation modulo 2 (exclusive OR) to two digital representations of the corresponding fragments in adjacent frames.
- The arithmetic difference is the result of arithmetic subtraction of digital representations of the corresponding fragments in adjacent frames.
- Element - depending on the characteristics of the task, either an element or various types of differences acts as an element. The digital representation of an element is a bit string of length k. In the case of fragments or logical differences, k = n 1 * n 2 * bpp, and in the case of arithmetic differences, k = n 1 * n 2 * bpp + n 1 * n 2 , since an additional sign bit is required for each pixel of the window.
- The volume of the film (N f ) - the total number of elements in the film. N f = (N 1 * N 2 * M) / (n 1 * n 2 )
- Element frequency - the ratio of the number of occurrences of this element in the film to the volume of the film.
- Element base is a set of all elements present in the video stream and their frequencies. The power of the base of elements is denoted by N b .
- Element code - a binary code that allows you to uniquely identify an element in the database.
The basic idea of a fragmented compression method
The main idea of the fragmented compression method is to represent the video stream in the form of a chain of elements of length N f from the base of elements. Since the video stream is a set of meaningful images (frames) that change quite slowly over time, a significant correlation should be expected both between neighboring elements of one frame and between the corresponding elements in neighboring frames. This should lead to two effects:
- The relatively small base power (N b ) relative to the power of the set of all possible values of fragments (2 k f ) even with a sufficiently large volume of the film;
- Significant non-uniformity of frequencies of occurrence of various elements from the base of elements in the film. This should allow the use of effective entropy coding-compression algorithms for a chain of elements in a video stream.
Thus, the main idea of the method of fragmentary compression is to represent the video stream in the form of a well-compressible sequence of elements from some specially composed base of elements. The experiments conducted by the authors confirm this hypothesis.
The concept of the method allows compressing the video stream both without losses and with losses. In the case of lossy compression, both pre-processing (filtering) is possible, which makes it possible to smooth the original image, and post-processing, which consists in analyzing the base of elements and then extracting and removing from the video stream both random noise and visually redundant information. The joint use of pre- and post-processing allows you to create a new compressed video stream with the desired properties.
The method of fragmentary compression can be represented as a sequence of four steps:
- Formation of the base of elements. In case of lossy compression, preliminary filtering of the video stream frames is possible;
- Analysis of the obtained base of elements and its frequency characteristics;
- Construction of short codes for base elements;
- Formation of a compressed film transfer scheme.
These steps are discussed in more detail below.
Formation of the base of elements
The process of forming the base of elements is one of the most resource-intensive steps of the fragmented compression method. The final compression rate largely depends on how efficiently this step is performed.
Due to the extremely high requirements for speed, the algorithm for forming the base of elements is performed in several stages, with different algorithms and data structures being used at each step.
Formation of the base of frame elements is the first and easiest step. At this stage, the next frame is received from the video stream, its preliminary processing if necessary, and, depending on the type of element, the corresponding “pseudo-frame” is formed.
When viewing a pseudo-frame, the window is shifted n 2 pixels wide and n 1pixels in height. The figure shows an example of a frame N 1 = 30 rows by N 2 = 45 columns, viewing is performed using the square window n 1 = n 2 = 5. Thin lines in the figure highlight individual pixels, thick lines show the borders of the window, and the numbers inside the window show the serial number when viewing.
If the elements are logical or arithmetic differences, then the scan will result in the following set of differences:
For most real videos, the assumption is made that there is a significant correlation between the corresponding elements in adjacent frames. This is also evident in the table: most elements correspond to zero differences. To save memory, the resulting frame element base is compacted. First, sorting is done by some effective algorithm, and then matching elements are combined into one record. That is, instead of 48 zero differences in the compacted base there will be only one record.
At the second stage, the compressed base of the frame elements is recorded in a special buffer of elements - a separate memory area where many frame bases are accumulated, and then are written to the global storage in one large block. A feature of the buffer is that any element of it can be randomly accessed by index, i.e. in fact, it’s just a large array of elements located in RAM:
It is also worth noting that the frame element bases are written to the buffer “as is” without any additional sorting. This leads to the fact that the buffer contains a lot of ordered sequences of elements, but it is not ordered itself:
When there is not enough space to write the next frame base in the buffer, the procedure for updating the list of elements that have actually met is called.
At the third stage, the elements accumulated in the buffer are moved to a special global storage, which is a singly connected list of elements sorted by their values. Representation of the global storage in the form of a list does not allow random access for constant time, but it allows you to add and remove items in constant time.
Before adding items from the buffer to the global storage, the sorting and compaction procedure of the buffer, as previously discussed, is performed. This allows you to add items in a linear time relative to the size of the list:
The three stages considered operate on data located in RAM. The final stage involves working with data stored on hard drives. In the overwhelming majority of cases, a sufficiently powerful modern computer allows you to completely assemble the base of elements in RAM, but there are situations when the size of RAM is not enough to fit the entire base there (for example, if the formation of a common base for hundreds of hours of shooting is performed). In this case, it is necessary to save the received databases to disk as the RAM runs out, and then perform the database merge procedure.
Thus, in the process of forming the base of elements, the following sequence of steps is performed:
Analysis of the obtained base of elements and its frequency characteristics
The analysis of the base of elements involves the analysis of both the individual values of each element and the frequency characteristics of the base. This allows, firstly, to choose effective combinations of compression methods (constructing short codes and methods of their transmission), and, secondly, in the case of compression with losses, consciously reduce the base (filtering).
Building short codes for base elements
The base of elements includes an array of N b lines of length k bits and a table of frequencies of occurrence of these lines in the video stream (film). This information is sufficient for applying well-known methods of entropy coding (Huffman tree, arithmetic coding, etc.). The above algorithms have very high estimates of efficiency, but their real use is associated with significant implementation difficulties.
To construct short codes of elements, the authors propose and use the previously proposed method for constructing prefix codes using secant functions. In this method, short codes of the base elements are built based on the content of the lines of the elements themselves. The author has proved that the average length of such codes does not exceed the value of H b * 1,049, where H b- entropy of the element base, calculated by the frequencies of the appearance of elements in the video stream. In numerical experiments with real films, H b never exceeded 20, which means that H b * 1,049
Formation of a compressed movie transmission scheme
In a compressed video stream, elements are replaced by previously obtained short codes. When playing a compressed video stream, a decoding problem occurs. For decoding, it is necessary to have information on the correspondence of short codes and base elements. The easiest way to transmit such information is to directly transmit the element and its frequency (number of occurrences). This method involves the transfer of the base itself, as well as an additional 64 bits per element. After receiving the data, the receiving party itself must build the code tree according to a previously reported algorithm.
A method was proposed for recording and transmitting a tree, in the leaves of which the entire base of elements was recorded. In this case, the transmission volume is equal to the volume of the base plus two additional bits for each element of the base ((k + 2) * N b ).
Let's agree on the tree traversal order: for example, we will use the width traversal. If a dividing tree node is found, bit 0 is transmitted, if a leaf was found during the traversal, bit 1 and the corresponding base element are transmitted. As a result, it is easy to show that only 2 extra bits are additionally transmitted to each base element. The figure shows the representation of a binary tree as a binary string using the described method:
The specified representation is reversible: for each line constructed in the described way, you can build the original code tree. In addition to the obvious memory savings, the described transmission method eliminates the need to build a code tree during decoding (it is restored naturally). That is, the code tree is built only once during compression.
Thus, the paper proposes a video stream transmission scheme consisting of two parts: a code tree with base elements and a chain of compressed element codes.
An approximate structure of the compressed video stream is shown in the figure:
Selection of algorithm parameters
The compression ratio provided by the fragmented compression algorithm largely depends on the properties and characteristics of the formed base of elements. The main characteristics of the base are the size (number of elements) and frequency characteristics (primarily entropy).
To assess the achievable compression ratio, we use the following formulas. Let l sr be the average length of the base element codes, then the amount of compressed transmission is V sr = N b (k + 2) + l sr * N f , and the volume of an uncompressed film is equal to V f = N f * k.
Compression ratio value will be called:
R SJ = V SJ / V f. Contact the compression ratio value is called the compression ratio and is denoted K SJ .
The main goal to strive for is to maximize K sr . In the formula above, N 1 , N 2 , M, bpp are the characteristics of the original video stream, which we cannot influence. And the values of l cf , N of the base depend on the area and configuration of the scan window (n 1 , n 2 ). Those. the only variable parameters in the method of fragmentary compression are the geometric dimensions of the window.
For any window size, there is the maximum possible base size equal to 2 bpp * n 1 * n 2, and this value is growing extremely fast. Of course, not all possible elements are found in real films, but with an increase in the size of the window, the number of bits necessary to represent the corresponding base element also increases. In addition, a significant amount (over 70% of the total number) of elements appears that are found in the video stream no more than once. Ultimately, all of these effects lead to a decrease in compression ratio.
On the other hand, too small a window size will lead to an increase in N f and a restriction of N b , which in turn will lead to the fact that the elements will be repeated more evenly and the “distortion” of frequencies will be smoothed out. The more evenly the elements are repeated to the base, the closer its entropy is to log 2 N b. This, in turn, also leads to a decrease in compression ratio.
Consider the two extreme cases of window 1 * 1 and window N 1 * N 2 . In both the first and second cases, K cr ≈1. In the process of research, it was found that the dependence of K Comp on the area of the scan window (n 1 * n 2 ) has approximately the following form:
The task is to find the point where the compression level is maximum. Because the compression level also largely depends on the characteristics of the film, it is clear that there is no “ideal” configuration that will give optimal compression for all films. But experiments allowed us to find a relatively small area where compression is optimal.
All analyzed video streams were divided into two groups depending on their features:
- Natural shooting. This group includes most films, television shows and amateur filming. Movies of this group are characterized by a smooth change of frames over time. In this case, the changes are quite smooth and concentrated in the center of the frame. The background in most cases is uniform, but slight fluctuations in brightness are possible.
To select the optimal window configuration, video streams belonging to each group were compressed using the fragmentary compression method. During the study, all possible window configurations with an area of one to eight pixels were analyzed (logical differences were used as elements). In total, about ten thousand hours of video were analyzed, which is about a billion frames. The results are presented in graphs.
From the presented data, it is obvious that the maximum compression ratio can be achieved by using windows with an area of three, four or five pixels. Also, in the practical use of the method of fragmentary compression of the video stream, it should be taken into account that for a fixed window area, the greatest compression efficiency is observed when using a rectangular window with an aspect ratio of close to 2/1.
Video stream coding in various color spaces
The previously reviewed results related to the coding of a video stream containing only the luminance component (the so-called monochrome video stream). Of great practical interest are methods that allow you to encode color video streams.
The easiest way to encode a color video stream is to independently encode color channels. A method was also considered in which element bases assembled for independent color channels were combined into one common base. Despite the fact that the share of the base in the transmission was decreasing, the increase in compression efficiency was negligible. It was also shown that the efficiency of the fragment compression method in the YIQ space is significantly higher than in the RGB space. First of all, this effect is associated with losses that occur when converting color spaces.
It is also worth noting that the compression efficiency in the YIQ space can be significantly improved due to coarse quantization of color difference channels.
Comparison of the effectiveness of the method of fragmented compression of the video stream with the methods used
Today, there are methods that allow you to compress video streams without loss. Some of them are highly specialized and effective on only one type of video stream (for example, on screen recording), other methods are effective on various video streams. This section is devoted to comparing the effectiveness of the proposed method of fragmented compression of a video stream with known methods.
In Graphics & Media Lab Video Group at Moscow State University Lomonosov made an extensive comparison of lossless video compression algorithms for a variety of parameters (compression speed, resource consumption, compression efficiency, etc.). The most important characteristic is compression efficiency. According to this criterion, the following codecs were analyzed:
- Alpary
- Arithyuv
- Avizlib
- CamStudio GZIP
- Corepng
- Fastcodec
- Ffv1
- Huffyuv
- Lagarith
- LOCO
- Lzo
- MSU Lab
- Picvideo
- Snow
- x264
- Yuls
Comparison was performed on standard test sequences. Each video sequence was compressed by each codec independently. The results obtained are shown in the graph:
For the convenience of analysis, the obtained values of the compression coefficients were averaged, and the obtained average estimates are given below:
Direct application of the method of fragmentary compression on these test video sequences is ineffective. This is because the duration of the test video streams is very short and a significant part in the film compressed by the method of fragmentary compression is the element base:
With a sufficient duration of the video stream (from 5000 frames), the average compression ratio of the fragmentary compression method is 3.38, which exceeds the compression coefficients of the best of the considered methods.
If the community is interested, I will talk about the secant tree, which allowed us to achieve such a very good result.
