DICOM Viewer from the inside. Voxel render
Good afternoon, dear Habra community!
Today I would like to shed light on one of the most unlit topics on the Habr. It will be about the visualizer of medical radiological images or DICOM Viewer'e. It is planned to write several articles in which we will talk about the main features of DICOM Viewer, including the capabilities of the voxel render, 3D, 4D, consider its device, support for the DICOM protocol, etc. In this article I will talk about the voxel render and its device. Everyone interested welcome to cat.
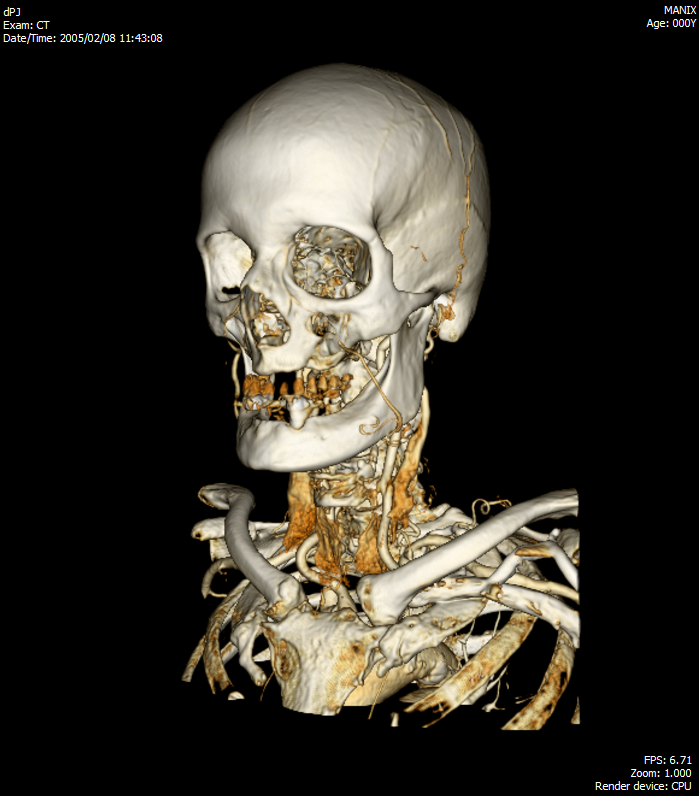
The company I work for has extensive experience in the development of medical software. I had a chance to work with some projects, so I wanted to share my experience in this area and show what we did. I would also like to take this opportunity and get feedback from X-ray doctors on the use of Viewer.
One of our products is DICOM Viewer - a medical image viewer in the DICOM format. It can render 2D images, build 3D models based on 2D slices, and also supports operations for both 2D images and 3D models. I will write about the operations and capabilities of the Viewer in the next article. At the end of the article, links to the DICOM Viewer with full functionality, which is described in the article and to the data for the samples, will be indicated. But first things first.
To imagine how to build a 3D model, for example, of the brain, from 2D DICOM files, you need to understand how images are represented in medicine. To begin with, all modern tomographs (MRI, CT, PET) do not produce ready-made images. Instead, a file is generated in a special DICOM format, which contains information about the patient, the study, as well as information for rendering the image. In fact, each file represents a slice of an arbitrary part of the body, in any plane, most often in the horizontal. So, each such DICOM file contains information about the intensity or density of tissues in a particular section, on the basis of which the final image is built. In fact, intensity and density are different concepts. Computed tomography stores x-ray density in files, which depends on the physical density of the tissues. Bones have a greater physical density, less blood, etc. A magnetic resonance imager maintains the intensity of the return signal. We will use the term density, thus generalizing the concepts described above.
Density information in a DICOM file can be represented as a regular image that has a resolution, pixel size, format and other data. Only instead of color information in a pixel is information on tissue density stored.
The diagnostic station produces not one file, but several for one study at once. These files have a logical structure. Files are combined in a series and are a set of consecutive slices of any organ. Series combine in stages. Stage defines the whole study. The sequence of the series in the stage is determined by the research protocol.
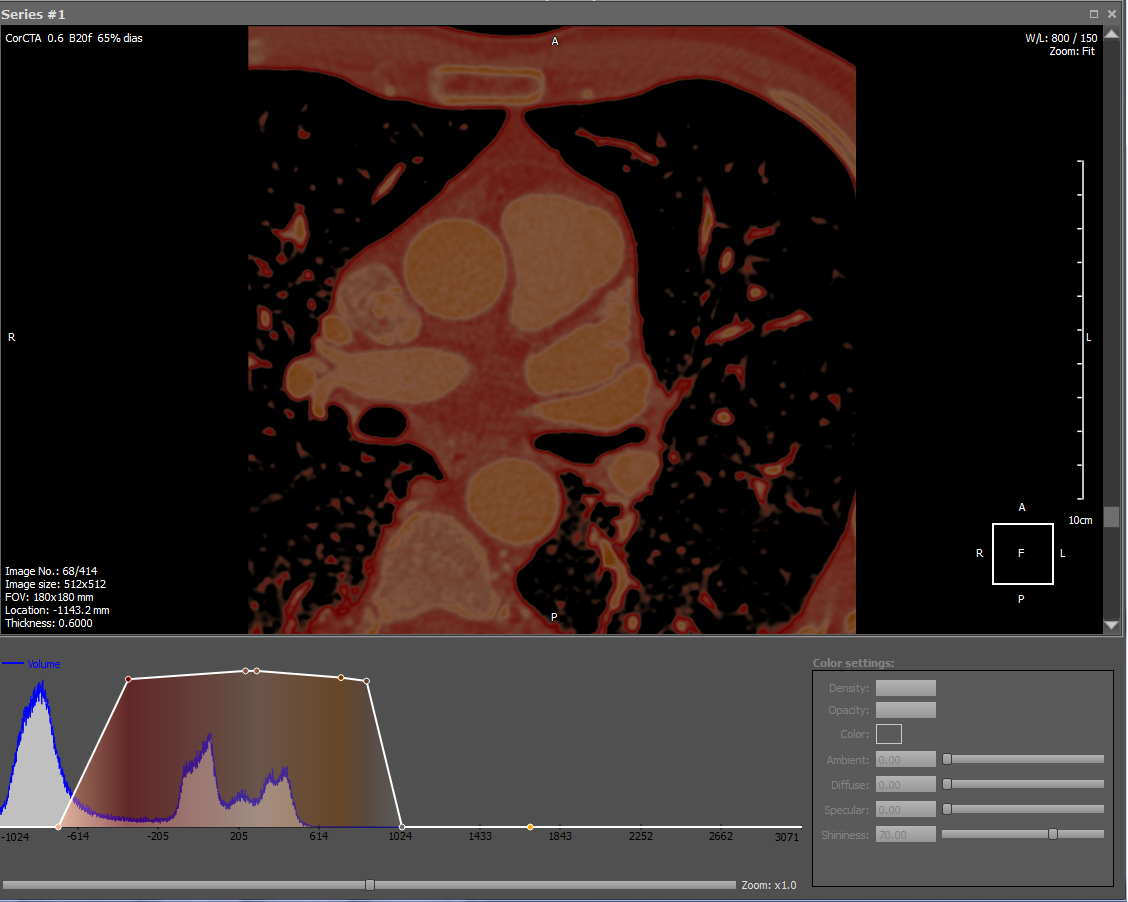
Information about tissue density in a DICOM file is the basis for its rendering. To draw an image you need to match the color values of the density. This is done by the transfer function, which in our viewer can be edited. In addition, there are many ready-made presets for rendering fabrics of different densities in different colors. Here is an example of a transfer function and the result of rendering:

The graph shows two white dots at the ends of the white line, which means that only white will be drawn. The line connecting the dots indicates opacity, i.e. less dense fabrics are drawn with more transparent pixels. Thus, white plus the corresponding opacity gives gradations of white, as can be seen in the picture. In this example, the relative transfer function is shown, so the percent is plotted on the abscissa. The blue graph shows the distribution of tissue densities, where each density value corresponds to the number of pixels (voxels) per given density.
In our render, a white color is drawn with the corresponding transparency on a black background, black color is never drawn. Such a scheme is convenient when rendering a 3D model - the air has a low density, therefore it is drawn transparent, so when applying slices through the air of the overlay image, the lower one will be visible. In addition, if the color had not a constant characteristic, but a linear one (which characterizes the transition from black to white), then multiplying the color by transparency (which also has a linear characteristic), a quadratic characteristic would be obtained that would reflect the color differently, which not true.
Transfer functions are divided by type into absolute and relative. The absolute transfer function is constructed for all possible densities. For CT, thisHounsfield scale (-1000 to ~ 3000). A density of -1000 corresponds to air, a density of 400 corresponds to bones, a zero density corresponds to water. For densities on the Hounsfield scale, the following statement is true: each density corresponds to a specific type of fabric. However, this statement is not true for MRI, since the MRI tomograph generates its own set of densities for each series. That is, for two series the same density can correspond to different body tissues. In an absolute transfer function, the arguments correspond to absolute density values.
The relative transfer function is built on the basis of the so-called window, which indicates which density range to draw. The window is determined by the Window Width (W) and Window Center (L) parameters, the recommended values of which are set by the tomograph and stored in image files in the corresponding DICOM tags. The values of W and L can be changed at any time. Thus, the window limits the domain of the transfer function. In a relative transfer function, the arguments correspond to the relative values given in percent. An example of the transfer function is shown in the figure above with a percentage scale from 0 to 100.
Both in the case of the absolute and in the case of the relative transfer function, there may be cases when the transfer function does not cover all the densities contained in the image file. In this case, all the densities that fall to the right of the transfer function take the values of the rightmost value of the transfer function, and the densities to the left of the leftmost value of the transfer function, respectively.
An example of an absolute transfer function in which the density is given in absolute values on the Hounsfield scale:
Here is an example of a more complex transfer linear function that colors densities in several colors:

As in the previous figure, transparency has a linear characteristic. However, colors are specified for specific densities. In addition to color, each of these points determines transparency (in accordance with the white line in the graph). In the case of a 3D model, each of the points also stores reflective components. Between specific points, interpolation is performed separately for each component, including transparency, RGB, and reflective components, thus obtaining values for the remaining densities.
Transparency in the transfer function does not have to be linear. She can be of any order. An example of a transfer function with arbitrary transparency:

Among other things, image information is drawn on each 2D image. An orientation cube is drawn in the lower right corner, according to which you can understand how the patient is located in this image. H - head (head), F - foot (legs), A - anterior (full face), P - posterior (back), L - left (left side), R - right (right side). The same letters are duplicated in the middle of each side. In the lower left and upper right corners for X-ray doctors, information is displayed on the parameters of the tomograph with which this image was obtained. Also on the right is the ruler and scale of one division, respectively.
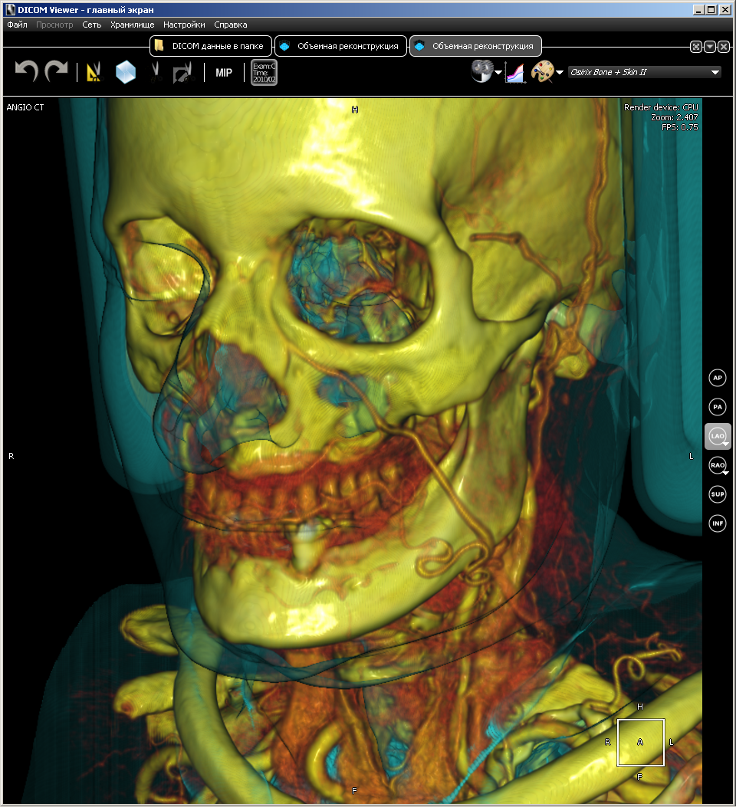
Since the voxel render is the basis for several of our projects, it is presented as a separate library. It is called VVL (Eng. Volume Visualization Library). It is written in pure C without the use of any third-party libraries. VVL is intended for rendering three-dimensional models built from data from DICOM scanners (MRI, CT, PET). VVL uses all the advantages of modern multi-core processors for realtime rendering, so it can work on a regular machine, and also has an implementation on CUDA, which gives much higher performance than on a CPU. Here is a pair of images obtained by rendering based on computed tomography data.

VVL implements the entire rendering process, starting with building a model and ending with the generation of a 2D image. There are such chips as resampling, antialiasing, translucency.
A voxel is an element of a three-dimensional image containing the value of an element in three-dimensional space. In the general case, anything, including color, can act as a voxel value. In our case, the density is the value of the voxel. As for the shape of the voxel, in the general case, the voxels can be cubic, or can be parallelepiped. Our voxels are presented in the form of cubes for simplification and convenience of work. Voxels do not store the coordinates; they are calculated from the relative location of the voxel.
In fact, a voxel is a complete analogue of a pixel in 3D. Pixel (English picture element) - an image element, Voxel (English volume element) - a volume element. Almost all the characteristics of the pixel are transferred to the voxel, so you can safely draw an analogy, given the dimension. Thus, voxels are used to represent three-dimensional objects:

In the screenshot, you can see small cubic voxels. To store density in a voxel, a 2 byte number is used. Therefore, you can calculate the size of the model: 2 bytes per density * number of voxels. Some voxel renders, in addition to the above, store information for rendering in the voxel, which requires additional memory. In practice, we have found that this is impractical and the necessary data is more advantageous to calculate on the fly than to store extra bytes.
The input data for the voxel render is the DICOM series, i.e. several images representing any area of the body. If the images of one series are superimposed on each other in the sequence and in the plane in which they were made, you can get a 3D model. One can imagine this somehow:

Since the DICOM protocol does not clearly declare in which tag the distance between images in a series is stored, it is necessary to calculate the distance between images from other data. So, each image has coordinates in space and orientation. This data is enough to determine the distance between images. Thus, having the image resolution and the distance between them in the series, you can determine the voxel size. The image resolution in X and Y is usually the same, i.e. The pixel has a square shape. But the distance between the images may differ from this value. Therefore, the voxel may be in the form of an arbitrary parallelepiped.
For ease of implementation and ease of use, we resample for density using bicubic filtering(Mitchell filter), and we get the cubic form of a voxel. If the pixel size is less than the distance between the slices, then we add slicers (supersampling), and if the pixel size is larger, then remove the slices (downsampling). Thus, the pixel size becomes equal to the distance between the slices and we can build a 3D model with a cubic voxel shape. Simply put, we adjust the distance between the images to the resolution of the image.
The resulting voxels are stored in a structure that is an array optimized for access in an arbitrary direction of movement, in the case of rendering on the processor. The array is logically divided into parallelepipeds, stored in memory by a continuous piece of ~ 1.5 kb in size with a voxel size of 2 bytes, which allows you to put several closely spaced parallelepipeds in the cache of the first-level processor. Each box stores 5x9x17 voxels. Based on the size of such a parallelepiped, the coordinates of the displacements in the total voxel array are calculated and stored in 3 separate arrays xOffset, yOffset, zOffset. Therefore, the array is accessed as follows: m [xOffest [x] + yOffset [y] + zOffset [z]]. Thus, starting to read data in the parallelepiped, we force the processor to put the entire parallelepiped into the cache of the first level processor,
In the case of rendering on the GPU, a special three-dimensional structure is used in the graphics memory of the video card, called a 3D texture, in which access to the voxels is optimized by means of a video adapter.
Raytracing - as a way of rendering. We move along the ray with a certain step and look for the intersection with the voxel and carry out trilinear interpolation at each step, where 8 vertices represent the midpoints of neighboring voxels. The CPU uses an octo tree as an optimal structure for quickly skipping transparent voxels. On a GPU for 3D texture, trilinear interpolation is performed automatically by the video card. The GPU does not use an octo-tree to skip transparent pixels, since in the case of a 3D texture it sometimes turns out that it is faster to take into account all voxels than to spend time searching and skipping transparent ones. Phong shading is
used as a lighting model., which allows you to make the image voluminous and gives a good picture and at the same time does not interfere with the work of X-ray doctors. Raytrace is made taking into account the transparency of voxels, which allows rendering translucent fabrics.
The render supports perspective

and parallel projection modes.

Perspective projection is more realistic. Moreover, it is necessary for virtual endoscopy, which I will discuss in the next article.
As I promised links to DICOM Viewer and the data for the test.
Today I would like to shed light on one of the most unlit topics on the Habr. It will be about the visualizer of medical radiological images or DICOM Viewer'e. It is planned to write several articles in which we will talk about the main features of DICOM Viewer, including the capabilities of the voxel render, 3D, 4D, consider its device, support for the DICOM protocol, etc. In this article I will talk about the voxel render and its device. Everyone interested welcome to cat.

The company I work for has extensive experience in the development of medical software. I had a chance to work with some projects, so I wanted to share my experience in this area and show what we did. I would also like to take this opportunity and get feedback from X-ray doctors on the use of Viewer.
One of our products is DICOM Viewer - a medical image viewer in the DICOM format. It can render 2D images, build 3D models based on 2D slices, and also supports operations for both 2D images and 3D models. I will write about the operations and capabilities of the Viewer in the next article. At the end of the article, links to the DICOM Viewer with full functionality, which is described in the article and to the data for the samples, will be indicated. But first things first.
Representation of images in medicine
To imagine how to build a 3D model, for example, of the brain, from 2D DICOM files, you need to understand how images are represented in medicine. To begin with, all modern tomographs (MRI, CT, PET) do not produce ready-made images. Instead, a file is generated in a special DICOM format, which contains information about the patient, the study, as well as information for rendering the image. In fact, each file represents a slice of an arbitrary part of the body, in any plane, most often in the horizontal. So, each such DICOM file contains information about the intensity or density of tissues in a particular section, on the basis of which the final image is built. In fact, intensity and density are different concepts. Computed tomography stores x-ray density in files, which depends on the physical density of the tissues. Bones have a greater physical density, less blood, etc. A magnetic resonance imager maintains the intensity of the return signal. We will use the term density, thus generalizing the concepts described above.
Density information in a DICOM file can be represented as a regular image that has a resolution, pixel size, format and other data. Only instead of color information in a pixel is information on tissue density stored.
The diagnostic station produces not one file, but several for one study at once. These files have a logical structure. Files are combined in a series and are a set of consecutive slices of any organ. Series combine in stages. Stage defines the whole study. The sequence of the series in the stage is determined by the research protocol.
2D render
Information about tissue density in a DICOM file is the basis for its rendering. To draw an image you need to match the color values of the density. This is done by the transfer function, which in our viewer can be edited. In addition, there are many ready-made presets for rendering fabrics of different densities in different colors. Here is an example of a transfer function and the result of rendering:

The graph shows two white dots at the ends of the white line, which means that only white will be drawn. The line connecting the dots indicates opacity, i.e. less dense fabrics are drawn with more transparent pixels. Thus, white plus the corresponding opacity gives gradations of white, as can be seen in the picture. In this example, the relative transfer function is shown, so the percent is plotted on the abscissa. The blue graph shows the distribution of tissue densities, where each density value corresponds to the number of pixels (voxels) per given density.
In our render, a white color is drawn with the corresponding transparency on a black background, black color is never drawn. Such a scheme is convenient when rendering a 3D model - the air has a low density, therefore it is drawn transparent, so when applying slices through the air of the overlay image, the lower one will be visible. In addition, if the color had not a constant characteristic, but a linear one (which characterizes the transition from black to white), then multiplying the color by transparency (which also has a linear characteristic), a quadratic characteristic would be obtained that would reflect the color differently, which not true.
Transfer functions are divided by type into absolute and relative. The absolute transfer function is constructed for all possible densities. For CT, thisHounsfield scale (-1000 to ~ 3000). A density of -1000 corresponds to air, a density of 400 corresponds to bones, a zero density corresponds to water. For densities on the Hounsfield scale, the following statement is true: each density corresponds to a specific type of fabric. However, this statement is not true for MRI, since the MRI tomograph generates its own set of densities for each series. That is, for two series the same density can correspond to different body tissues. In an absolute transfer function, the arguments correspond to absolute density values.
The relative transfer function is built on the basis of the so-called window, which indicates which density range to draw. The window is determined by the Window Width (W) and Window Center (L) parameters, the recommended values of which are set by the tomograph and stored in image files in the corresponding DICOM tags. The values of W and L can be changed at any time. Thus, the window limits the domain of the transfer function. In a relative transfer function, the arguments correspond to the relative values given in percent. An example of the transfer function is shown in the figure above with a percentage scale from 0 to 100.
Both in the case of the absolute and in the case of the relative transfer function, there may be cases when the transfer function does not cover all the densities contained in the image file. In this case, all the densities that fall to the right of the transfer function take the values of the rightmost value of the transfer function, and the densities to the left of the leftmost value of the transfer function, respectively.
An example of an absolute transfer function in which the density is given in absolute values on the Hounsfield scale:

Here is an example of a more complex transfer linear function that colors densities in several colors:

As in the previous figure, transparency has a linear characteristic. However, colors are specified for specific densities. In addition to color, each of these points determines transparency (in accordance with the white line in the graph). In the case of a 3D model, each of the points also stores reflective components. Between specific points, interpolation is performed separately for each component, including transparency, RGB, and reflective components, thus obtaining values for the remaining densities.
Transparency in the transfer function does not have to be linear. She can be of any order. An example of a transfer function with arbitrary transparency:

Among other things, image information is drawn on each 2D image. An orientation cube is drawn in the lower right corner, according to which you can understand how the patient is located in this image. H - head (head), F - foot (legs), A - anterior (full face), P - posterior (back), L - left (left side), R - right (right side). The same letters are duplicated in the middle of each side. In the lower left and upper right corners for X-ray doctors, information is displayed on the parameters of the tomograph with which this image was obtained. Also on the right is the ruler and scale of one division, respectively.
Voxel render
What is it ?
Since the voxel render is the basis for several of our projects, it is presented as a separate library. It is called VVL (Eng. Volume Visualization Library). It is written in pure C without the use of any third-party libraries. VVL is intended for rendering three-dimensional models built from data from DICOM scanners (MRI, CT, PET). VVL uses all the advantages of modern multi-core processors for realtime rendering, so it can work on a regular machine, and also has an implementation on CUDA, which gives much higher performance than on a CPU. Here is a pair of images obtained by rendering based on computed tomography data.


VVL implements the entire rendering process, starting with building a model and ending with the generation of a 2D image. There are such chips as resampling, antialiasing, translucency.
Voxel model inside
A voxel is an element of a three-dimensional image containing the value of an element in three-dimensional space. In the general case, anything, including color, can act as a voxel value. In our case, the density is the value of the voxel. As for the shape of the voxel, in the general case, the voxels can be cubic, or can be parallelepiped. Our voxels are presented in the form of cubes for simplification and convenience of work. Voxels do not store the coordinates; they are calculated from the relative location of the voxel.
In fact, a voxel is a complete analogue of a pixel in 3D. Pixel (English picture element) - an image element, Voxel (English volume element) - a volume element. Almost all the characteristics of the pixel are transferred to the voxel, so you can safely draw an analogy, given the dimension. Thus, voxels are used to represent three-dimensional objects:

In the screenshot, you can see small cubic voxels. To store density in a voxel, a 2 byte number is used. Therefore, you can calculate the size of the model: 2 bytes per density * number of voxels. Some voxel renders, in addition to the above, store information for rendering in the voxel, which requires additional memory. In practice, we have found that this is impractical and the necessary data is more advantageous to calculate on the fly than to store extra bytes.
Representation of model in memory
The input data for the voxel render is the DICOM series, i.e. several images representing any area of the body. If the images of one series are superimposed on each other in the sequence and in the plane in which they were made, you can get a 3D model. One can imagine this somehow:

Since the DICOM protocol does not clearly declare in which tag the distance between images in a series is stored, it is necessary to calculate the distance between images from other data. So, each image has coordinates in space and orientation. This data is enough to determine the distance between images. Thus, having the image resolution and the distance between them in the series, you can determine the voxel size. The image resolution in X and Y is usually the same, i.e. The pixel has a square shape. But the distance between the images may differ from this value. Therefore, the voxel may be in the form of an arbitrary parallelepiped.
For ease of implementation and ease of use, we resample for density using bicubic filtering(Mitchell filter), and we get the cubic form of a voxel. If the pixel size is less than the distance between the slices, then we add slicers (supersampling), and if the pixel size is larger, then remove the slices (downsampling). Thus, the pixel size becomes equal to the distance between the slices and we can build a 3D model with a cubic voxel shape. Simply put, we adjust the distance between the images to the resolution of the image.
The resulting voxels are stored in a structure that is an array optimized for access in an arbitrary direction of movement, in the case of rendering on the processor. The array is logically divided into parallelepipeds, stored in memory by a continuous piece of ~ 1.5 kb in size with a voxel size of 2 bytes, which allows you to put several closely spaced parallelepipeds in the cache of the first-level processor. Each box stores 5x9x17 voxels. Based on the size of such a parallelepiped, the coordinates of the displacements in the total voxel array are calculated and stored in 3 separate arrays xOffset, yOffset, zOffset. Therefore, the array is accessed as follows: m [xOffest [x] + yOffset [y] + zOffset [z]]. Thus, starting to read data in the parallelepiped, we force the processor to put the entire parallelepiped into the cache of the first level processor,
In the case of rendering on the GPU, a special three-dimensional structure is used in the graphics memory of the video card, called a 3D texture, in which access to the voxels is optimized by means of a video adapter.
Rendering
Raytracing - as a way of rendering. We move along the ray with a certain step and look for the intersection with the voxel and carry out trilinear interpolation at each step, where 8 vertices represent the midpoints of neighboring voxels. The CPU uses an octo tree as an optimal structure for quickly skipping transparent voxels. On a GPU for 3D texture, trilinear interpolation is performed automatically by the video card. The GPU does not use an octo-tree to skip transparent pixels, since in the case of a 3D texture it sometimes turns out that it is faster to take into account all voxels than to spend time searching and skipping transparent ones. Phong shading is
used as a lighting model., which allows you to make the image voluminous and gives a good picture and at the same time does not interfere with the work of X-ray doctors. Raytrace is made taking into account the transparency of voxels, which allows rendering translucent fabrics.
The render supports perspective

and parallel projection modes.

Perspective projection is more realistic. Moreover, it is necessary for virtual endoscopy, which I will discuss in the next article.
As I promised links to DICOM Viewer and the data for the test.
