Where is the death of Kashcheev?
Hi guys, let's check your memory first. So:
 And now, attention, the question is how to formalize this?
And now, attention, the question is how to formalize this?
How to attach a needle to an egg and what is the time complexity of the child of my death. How to transfer a fairy tale to the past, how it looks on B-trees and why there really is no difference between 2D and 1D.
And it was like this: a long time ago, in a certain kingdom, some state, on the same service with geolocation shearing, Ivanushka the Fool really wanted to divide Moscow (/ RU / MOW /) and Region (/ RU / MOS /) at the CNC level . And in general, put things in order so that everything is on the shelves beautifully and alphabetically. But he did not succeed in counting his treasures, and carefully decomposing them. And Vasilisa, though a fool, did not allow his savings.
But a solution was found.
Very close to some kind of gold was the chakh Chakhlik successfully, and he also hid his death in science.
And if the task of determining the regional (or rather polygonal) affiliation of a certain needle to a certain chest is beyond the scope of this article, then nothing prevents us from plunging into the depths of a hare and seeing how it works at a table level.
PS: and don’t ask why a hare.
So - the initial task is to determine some entries in certain categories, but let's clarify the TK:
In general, the task is to process certain elements that are attached to a certain tree of hierarchies.
Let's start with a simple one - and the implementation of categories, directories or just trees. There are not many options for implementation, or rather a normalized version of the implementation, in general, seems to be one:
There is a certain element, and it has one parent (if two - no longer trees). This all works well until we need to perform some operations on the branches .
These problems are relevant for headings on the site, and files on the disk, and generally purely theoretical sofa studies.
And there are several standard solutions to this problem:

But this is what we will understand, because the Nested set table ( http://en.wikipedia.org/wiki/Nested_set_model ) is :

The difference from the "usual" child-parent schemes is that a certain parent contains two certain "numbers" - the beginning of its interval, and the end. And all his children contain “numbers” somewhere between these meanings. You can visualize in different ways; on Wikipedia you can find several scary tree options. But if you take an ordinary tree, divide by levels and draw on a piece of paper, you get lists with passes.
And with a wave of his wand, this picture turns into a B-tree. Because the difference, ideologically, is not.
In some way, nested-set addressing can be considered a kind of “space filling curve”, a kind of curve that inextricably recursively intersects all elements of a certain tree in the traversal order.
If the initial interval is set to 0-1, then divided at 1/2, and then 1 / 4,2 / 4,3 / 4,8 / 16,50 / 128 ... it turns out that any student who is in the first year tried to eat within and converging sequences - smoked my grass. Although in fact it is called the Stern Tree - Broco

For many, the hardest part about NS is building them. Many people are immediately scared by these left / right / st and other scary words and pictures used on various sites. Including on Habré, you can find a couple of articles about building NS in the database, including on storage and triggers . Personally, such articles scare me.
In fact, NS is just intervals, just a statement that children can be found somewhere in the corridor of parents' meanings. These are not trees, these are numbers that are stored in flat database tables. Continuous row on a numerical curve.
As a result, building NS is easier:
Option 1:
Option 2:
In both cases, insertion and deletion are O (n), and sometimes O (1).
NS is just two numbers, the interval between the “rolls” of which is hidden all the most delicious. In general, a curve does not have to consist of integers; moreover, it fits perfectly into fractions. We take the already mentioned Stern - Broco and get the Koch curve.
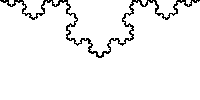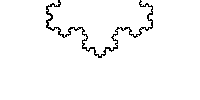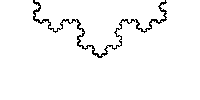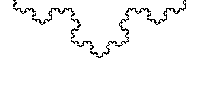
I hope you read up to this point, understand what Nested Intervals are, it remains to understand why they are so good.
Imagine that you have a list of all Hotellook (Aviasales) hotels. Imagine that you have a binding of these hotels in countries-regions-cities-districts. The task is to find all hotels in Orekhovo-Borisovo Yuzhnoye (narrow selection), all 5-star hotels in Turkey (large selection), and all hotels within a square of 100 meters from you.
Solution 1:
Solution to situation 2:
That is the secret - there is no difference . And in both cases it works fast.
The solution to situation 3 implies a certain coordinate search . But in ordinary databases, this is a very complicated and expensive operation — searching by a double key, or by a 2D (spatial) key — is simply complicated, expensive, and many reads are generated from different places on the disk. Well, simply because the order of data storage on a 1D drive.
But the solution to the situation remains almost the same:
Where we use Morton, it’s a Z-curve code for converting 2D coordinates to a 1D curve (it was written about this a couple of times on the Habré), and then we save it in Gray codes (two bits per division) and we can make quick samples from the pyramid ( hi ObjectManager ).
For many, it is not entirely clear why the samples are fast - you should probably explain. Morton codes, in addition to being “quadtree addressable,” have one more property - codes for objects that are nearby will be nearby.
Z is not the best solution, but it is great for quick sampling of groups (tiles) of objects. Z-codes “hold” the locality of the data, including for objects of the same node the codes will be generally the same, or their variability will be sandwiched between the left and right values of the NS element.
Plus - NS, as I said - a kind of materialization of skip-lists, a numerical curve or even B-trees. There is no technical difference. So when you store data in NS you store it in the B-tree ... then ... wait ...
In general, Z , Hilbert , GeoHash (Z codes in base64) and the company are the sameI NestedSet, view from the side.
These codes are often used in various GIS systems, including Bing called their quad-code and uses it for addressing tiles, and all this works without problems in 3D and 4D space.
Reducing problems into a simple numerical curve.
And in the standard NestedSet.

The effect is always the same - everything starts to work .
That’s the end of the tale, and whoever listened is well done.
PS: There were kashey and esosedi with you, who have been using NS and Z codes for selecting objects on the map for almost 7 years. Among which were HotelLook hotels (these arespecial.habrahabr.ru/aviasales ).
PPS: Join Fourier - Convergence! Equality! Hilbert space!
PPPS: And don't forget the wisdom of the ages!
“There is an island on the sea on the ocean, an oak tree stands on that island, a chest is buried under an oak tree, a hare is in a chest, a duck is in a hare, an egg is in a duck” - the needle is the death of Koshchei in the egg!
 And now, attention, the question is how to formalize this?
And now, attention, the question is how to formalize this? How to attach a needle to an egg and what is the time complexity of the child of my death. How to transfer a fairy tale to the past, how it looks on B-trees and why there really is no difference between 2D and 1D.
And it was like this: a long time ago, in a certain kingdom, some state, on the same service with geolocation shearing, Ivanushka the Fool really wanted to divide Moscow (/ RU / MOW /) and Region (/ RU / MOS /) at the CNC level . And in general, put things in order so that everything is on the shelves beautifully and alphabetically. But he did not succeed in counting his treasures, and carefully decomposing them. And Vasilisa, though a fool, did not allow his savings.
But a solution was found.
Very close to some kind of gold was the chakh Chakhlik successfully, and he also hid his death in science.
And if the task of determining the regional (or rather polygonal) affiliation of a certain needle to a certain chest is beyond the scope of this article, then nothing prevents us from plunging into the depths of a hare and seeing how it works at a table level.
PS: and don’t ask why a hare.
So - the initial task is to determine some entries in certain categories, but let's clarify the TK:
- There is a “ geolocation sharing ” - approximately 3 million points
- Which somehow “lie” in 300 thousand quarters, districts and other administrative divisions invested in each other.
- At any moment of time, it is required to find all objects that are included in at least the district of the city, even in the continent.
In general, the task is to process certain elements that are attached to a certain tree of hierarchies.
Let's start with a simple one - and the implementation of categories, directories or just trees. There are not many options for implementation, or rather a normalized version of the implementation, in general, seems to be one:
{
id: entity_id,
parent: parentId
}
There is a certain element, and it has one parent (if two - no longer trees). This all works well until we need to perform some operations on the branches .
- 1. Find all subheadings == find all areas of the city
- 2. Find all the elements in the subheadings == find all the objects of the city
- 3. Find all your parents up == understand in which country the city
- 4. Count, aggregate, break or repair something.
These problems are relevant for headings on the site, and files on the disk, and generally purely theoretical sofa studies.
And there are several standard solutions to this problem:

- 1. Adjacent Set (AL) - en.wikipedia.org/wiki/Adjacency_list
A table of the form child, parent [, level], where all the parents of the child are simply indicated . How many parents - how many records.
This is the simplest and most “normalized” option. It is absolutely convenient, but it can deliver very large “clouds” to the “exit” and generate kilometer “guts” of tables. Due to its large size and smearing, it works, in general, not instantly. - 2. Materialized Path (MP)
This is when we take all our parents and “materialize” in one line, separated by commas. And then we can use the LIKE operator to find the right one.
In principle, the normal option, beloved by students. Especially good if you go from the base 10, including the usual string, to a little more binary (base32.64.92 or 254).
There is only one minus - it’s not technologically advanced, and indexes in any place of the line do not work very well.
PS: there are also technological solutions - the so-called matrix trees, when the node ID is a matrix, and the positions of the elements are the determinants of their multiplication. Given the non-commutative multiplication, the key is real. If after reading this paragraph you thought about Tin - the way it is. - 3. Nested set (NS).
Nested set table is such a piece about which many have heard, but few know how it works and why. For many, NS is a plugin or library that you can use. And to understand - break.
But this is what we will understand, because the Nested set table ( http://en.wikipedia.org/wiki/Nested_set_model ) is :

- 1. One of the skip-list materializations
- 2. One of the B-tree materializations
- 3. Direct translation is simple - nested intervals
- 4. They are not scary at all.
- 5. Provide linear storage.
- 6. And they are exactly what we need
The difference from the "usual" child-parent schemes is that a certain parent contains two certain "numbers" - the beginning of its interval, and the end. And all his children contain “numbers” somewhere between these meanings. You can visualize in different ways; on Wikipedia you can find several scary tree options. But if you take an ordinary tree, divide by levels and draw on a piece of paper, you get lists with passes.
 |  |
And with a wave of his wand, this picture turns into a B-tree. Because the difference, ideologically, is not.
In some way, nested-set addressing can be considered a kind of “space filling curve”, a kind of curve that inextricably recursively intersects all elements of a certain tree in the traversal order.
If the initial interval is set to 0-1, then divided at 1/2, and then 1 / 4,2 / 4,3 / 4,8 / 16,50 / 128 ... it turns out that any student who is in the first year tried to eat within and converging sequences - smoked my grass. Although in fact it is called the Stern Tree - Broco

For many, the hardest part about NS is building them. Many people are immediately scared by these left / right / st and other scary words and pictures used on various sites. Including on Habré, you can find a couple of articles about building NS in the database, including on storage and triggers . Personally, such articles scare me.
In fact, NS is just intervals, just a statement that children can be found somewhere in the corridor of parents' meanings. These are not trees, these are numbers that are stored in flat database tables. Continuous row on a numerical curve.
As a result, building NS is easier:
Option 1:
In the database, we count the number of our children (COUNT (id)), and then the number of this number (count (count)). Thus, the "bubble method" full capacity rises up. It remains only to find your neighbor, and somehow take the offset from him - the full capacity of his neighbors to the left.
These are 4 SQL queries, some of which need to be performed a couple of times.
Okay not 4
CREATETABLEIFNOTEXISTS`flatindex` (`rid`int(11) NOTNULL,`lvl` tinyint(4) NOTNULL,`prev`int(11) NOTNULL,`parent`int(11) NOTNULL,`innerCnt`int(11) NOTNULL,`fullCnt`int(11) NOTNULL,`cumsum`int(11) NOTNULL,`start`int(11) NOTNULL,`right_key`int(11) NOTNULL,PRIMARY KEY (`rid`),KEY`parent` (`parent`),KEY`start` (`start`))
--INSERT INTO flatindex (rid,lvl) SELECT id,level FROM regions-- "Первая" операция-- innerCnt - количество подрубрик.-- В fullCnt "пузырьком" всплывает количество всех подрубрик--repeat until affected_rows=0UPDATE flatindex as fl1,(SELECT fl1.rid,sum(fl2.fullCnt)+fl1.innerCnt+1as cnt FROM flatindex as fl1 INNERJOIN flatindex as fl2 ON fl2.parent=fl1.rid GROUPBY fl1.rid) as gr SET fl1.fullCnt=gr.cnt WHERE fl1.rid=gr.rid
-- "Вторая операция"-- в cumsum записывается количество элементов "левее" в текущей рубрикеUPDATE flatindex as fl1,
(SELECTSUM(fl2.fullCnt)+COUNT(*) +1as fc,fl1.rid as rid
from flatindex as fl1
LEFTJOIN flatindex as fl2 ON fl2.parent=fl1.parent
WHERE fl2.rid<fl1.rid GROUPBY fl1.rid)as gr
SET fl1.cumsum=gr.fc WHERE gr.rid=fl1.rid
-- "Третья" операция-- заполняем первые позицииUPDATE flatindex SETstart=cumsum+1WHEREparent=0;
-- repeat until affected_rows=0UPDATE flatindex as fl,(SELECTstart,rid FROM flatindex)as gr SET fl.start=gr.start+1WHERE fl.prev=0and fl.parent=gr.rid;
UPDATE flatindex as fl,(SELECTstart,parentFROM flatindex WHERE prev=0)as gr SET fl.start=cumsum+gr.start WHERE prev!=0and fl.parent=gr.parent;
-- "Четвертая"-- установка правых значенийUPDATE flatindex SET right_key = start+fullCnt+1;
Option 2:
We convert our tree to matpath, sort through strnatsort and suspend some auto_incriment in this order. The numerical curve is ready. It remains only to find your neighbor (for example, on the right), and use his "number" as the right border.
In both cases, insertion and deletion are O (n), and sometimes O (1).
NS is just two numbers, the interval between the “rolls” of which is hidden all the most delicious. In general, a curve does not have to consist of integers; moreover, it fits perfectly into fractions. We take the already mentioned Stern - Broco and get the Koch curve.
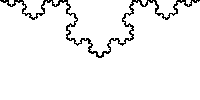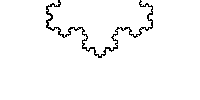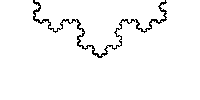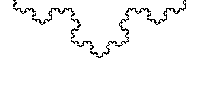
I hope you read up to this point, understand what Nested Intervals are, it remains to understand why they are so good.
Imagine that you have a list of all Hotellook (Aviasales) hotels. Imagine that you have a binding of these hotels in countries-regions-cities-districts. The task is to find all hotels in Orekhovo-Borisovo Yuzhnoye (narrow selection), all 5-star hotels in Turkey (large selection), and all hotels within a square of 100 meters from you.
Solution 1:
WHERE hotels_to_regions_ns.id between ns.left and ns.rightSolution to situation 2:
WHERE hotels_to_regions_ns.id between ns.left and ns.rightThat is the secret - there is no difference . And in both cases it works fast.
The solution to situation 3 implies a certain coordinate search . But in ordinary databases, this is a very complicated and expensive operation — searching by a double key, or by a 2D (spatial) key — is simply complicated, expensive, and many reads are generated from different places on the disk. Well, simply because the order of data storage on a 1D drive.
But the solution to the situation remains almost the same:
WHERE hotels_to_mortoncode.z between ns.zleft and ns.zrightWhere we use Morton, it’s a Z-curve code for converting 2D coordinates to a 1D curve (it was written about this a couple of times on the Habré), and then we save it in Gray codes (two bits per division) and we can make quick samples from the pyramid ( hi ObjectManager ).
For many, it is not entirely clear why the samples are fast - you should probably explain. Morton codes, in addition to being “quadtree addressable,” have one more property - codes for objects that are nearby will be nearby.
maps multidimensional data to one dimension while preserving locality of the data points
Z is not the best solution, but it is great for quick sampling of groups (tiles) of objects. Z-codes “hold” the locality of the data, including for objects of the same node the codes will be generally the same, or their variability will be sandwiched between the left and right values of the NS element.
Plus - NS, as I said - a kind of materialization of skip-lists, a numerical curve or even B-trees. There is no technical difference. So when you store data in NS you store it in the B-tree ... then ... wait ...
 |  |
In general, Z , Hilbert , GeoHash (Z codes in base64) and the company are the same
These codes are often used in various GIS systems, including Bing called their quad-code and uses it for addressing tiles, and all this works without problems in 3D and 4D space.
Reducing problems into a simple numerical curve.
And in the standard NestedSet.

The effect is always the same - everything starts to work .
That’s the end of the tale, and whoever listened is well done.
PS: There were kashey and esosedi with you, who have been using NS and Z codes for selecting objects on the map for almost 7 years. Among which were HotelLook hotels (these arespecial.habrahabr.ru/aviasales ).
PPS: Join Fourier - Convergence! Equality! Hilbert space!
PPPS: And don't forget the wisdom of the ages!
