Lock-free data structures. Concurrent maps: trees

This is the last, to date, article from the cycle about the internal structure of competitive associative containers. In previous articles, hash map was considered, the lock-free ordered list algorithm and containers based on it were built. One important type of data structure left behind is trees. It's time to talk a little about them.

Studies on competitive tree algorithms that do not require external synchronization of access to them began quite a long time ago - in the 70s of the last century - and were initiated by the development of the DBMS, therefore they related mainly to the optimization of page trees ( B-tree and its modifications).

The development of the lock-free approach in the early 2000s did not pass by tree algorithms, but only recently, in the 2010s, a lot of really interesting works on competitive trees appeared. Tree algorithms are quite complex, so the researchers took time - about 10 years - to lock-free / non-blocking their adaptation. In this article we will consider the simplest case - an ordinary binary tree, not even self-balancing.

What is the practical meaning of an ordinary binary tree, the reader will ask, because we all know that for ordered data such a tree degenerates into a linear list with the complexity of searching O (N)? The main point is to test approaches on a simple data structure. In addition, for random data, the binary tree works quite well, providing O (log N) complexity, and its internal simplicity is the key to high efficiency. So it all depends on the task where such a tree is used.

To begin with - a retrospective look at the problem of building lock-free / non-blocking trees. After quite effective lock-free algorithms for queues and lists were found, work appeared on lock-free self-balancing trees - AVL tree, Red-Black tree. The pseudo-code of these algorithms was complicated - so complicated that I wouldn’t want to implement it, because I don’t understand, for example, how to apply memory management schemes to them (Hazard Pointer, RCU or something else), the algorithms relied on garbage collector (GC) language, usually Java. In addition, I would not implement an algorithm that uses the CAS primitive (compare-and-swap) to searchkey in the tree - CAS is too heavy for this. Anyway, despite the formal proof of the correctness of such an algorithm (in the presence of GC, this reservation is essential, the absence of GC can violate the proof), its complexity, the presence of many boundary cases, seemed to me insurmountable in the light of debugging.

Apparently, not only me was scared of complexity and, according to developers, the inefficiency of the resulting lock-free algorithms for trees. Therefore, in the early 2010s, the emphasis in the development of algorithms shifted somewhat: instead of providing lock-free by any means, a lot of work began to appear, where the efficiency of the tree search operation was paramount. Indeed, trees are mainly used in search tasks (it is believed that the search is 70 - 90% of operations), and it is the search that should be fast. Therefore, non-blocking algorithms appeared in which the search is lock-free, and insert / delete can be locked at the level of a group of nodes (fine-grained locking) - either explicitly using mutexes, or implicitly using flags, etc., that is essentially spinning. This approach gave less complex and more understandable algorithms,

Binary search tree

We will consider a tree in which data is located in leaves, internal nodes are route and contain only keys:



This is the so-called leaf-oriented tree. The presence of the required key in the internal node does not mean that the key exists in the tree — only the leaves contain the keys and the corresponding data, the internal nodes may contain remote keys.

In such a tree, each node has exactly two descendants. Insertion into such a tree always generates one sheet and one internal node; when a key is deleted, one sheet and one internal node, its parent, are deleted. No balancing is provided.

Consider what surprises await us when performing competing operations. Let there be a certain tree and flows A and B delete keys 15 and 27, respectively:



Stream A to delete key 15 must delete the sheet with this key and its parent — the internal node with key 20. To do this, it changes the right link from its grandfather - node 10 - from node 20 to node 30, which is the brother of the deleted node. Since we are considering competitive trees, this operation should be performed atomically, that is, using CAS (compare-and-swap).

At the same time, stream B deletes key 27. Similarly to the above, stream B throws the right link of node 20 (grandfather 27) from 30 to sheet 45 by CAS.

If these two actions are performed in parallel, we will get reachable node 30 and reachable sheet 27 to be deleted.

When performing competing delete and insert, the situation is similar:



Here, thread A deleting the sheet with key 27 competes with thread B, which inserts the new key 29. To delete 27 (and its parent, internal node 30), thread A flips the pointer of the right son of node 20 from 30 to 45. At the same time, the key 29 and the corresponding internal node 29 are inserted as the left son of the node 30, in the same position from where thread A deletes the key 27. As a result, the new key becomes unreachable - memory leak.

Obviously, the CAS primitive alone cannot resolve the cases described above. Before inserting / deleting, you must somehow mark the nodes involved in the operation. The insert node involves the leaf node and its parent, the internal node. Before performing an insertion, the parent node should be marked “insertion is being performed” so that competing insertions / deletions cannot be performed on this node. The delete operation involves the deleted sheet, its parent and the parent of its parent - the grandfather of the deleted sheet. Both internal nodes - the parent and grandfather - should also be marked to exclude competition on them.

In this paper, it is proposed to use a status field for each internal node State: The



internal node can be in one of the following states:

• Clean- No insertions or deletes are performed on the node. This is the default node state.
• IFlag- the insert is performed into the node. This flag marks the internal node, in which at least one son is a leaf.
• DFlag- removal is in progress. This flag marks the internal grandfather of the sheet to be deleted.
• Mark- The internal node will be deleted. This flag marks the parent of the deleted sheet (remember that in our tree, when the sheet is deleted, its parent is also deleted).

These states are mutually exclusive: each node can be in only one of them. Changing the state of a node is performed by the CAS primitive
Recall that our main goal is the most efficient implementation of the key search operation in the tree. How do these conditions affect your search? Obviously, the insert operation and the corresponding flag IFlagcan be ignored during the search: when inserting, there are no deletions, which means we won’t be able to “enter the restricted, remote zone”. But flags DFlagand Markshould influence the search: when the unit with one of these flags search must be restarted from the beginning (there are possible actions variations, but the most simple - to start a new search).

So, let's see how these states work on the example of key 29 insertion:



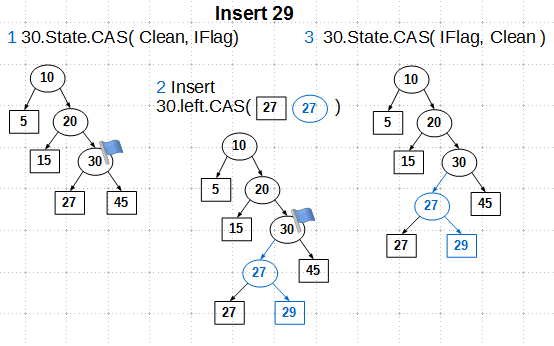
We find the insert node - this is internal node 30. First of all, we set the state of IFlagnode 30 to the CAS primitive. CAS here guarantees us that we will only go to the state IFlagfrom the state Clean, which excludes competing operations, that is, we become the exclusive owners of node 30. Next, we create an internal node 27, assign sons to it - the existing sheet 27 and the new 29, - and change the pointer the left son of node 30 to the newly created internal node 27. Why is CAS needed here, is it possible to get by with the usual atomic store? The answer is impossible in the original algorithm, in the implementation of libcds, you can use the atomic store, we'll talk about this later. And finally, the third step: remove the flagIFlagfrom node 30. CAS is also used here in the original algorithm, which can be replaced by an atomic store, if we refuse something not very necessary.

The delete operation using flags Stateconsists of four steps: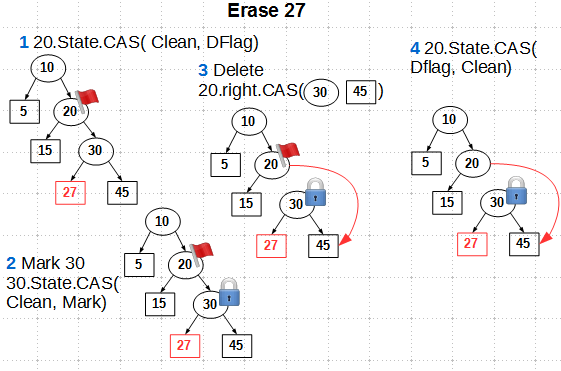

• Mark the grandfather of the deleted sheet DFlagwith state using CAS
• We mark the parent of the sheet to be deleted with the state MarkCAS as well
• Throw CAS'om pointer to the descendant of the grandfather node
• Unmark the DFlaggrandfather. CAS is used here, but a simpler atomic store can be used with some simplification of the algorithm

Note that Markwe do not remove the label from the parent node of the sheet to be deleted, since in our algorithm the parent is also deleted and it makes no sense to remove the label from it.

Let's see how the flags work in the case of competitive deletion. Without status flags, the competitive removal of keys 15 and 27 led to reachability of the deleted sheet, as we saw earlier:



With state flags, we have:



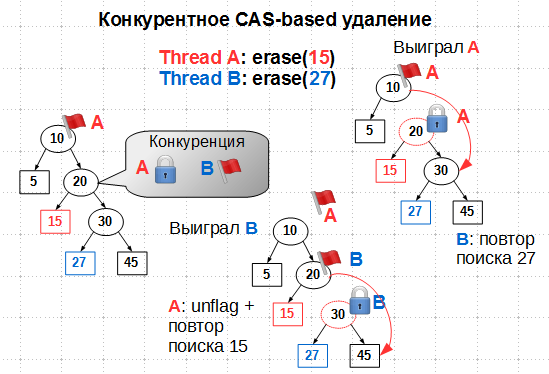
It would seem that if thread A set a flag DFlagon node 10, stream B should not go further than node 10 when searching 27. But our operations are carried out in parallel, so it is quite possible that thread B managed to sneak through node 10 before it was flagged DFlag. Then, competition arises on node 20: stream A wants to flag it Mark, stream B wants flagDFlag. Since the node state is set by atomic CAS from the state Clean, only one of the threads will win this battle. If thread A wins, that is, if it succeeds in flagging 20 with flag Mark, thread B begins to search for node 27 to be deleted from the beginning, and A deletes 15 and then removes the flag DFlagfrom 10. If B wins, by flagging 20 DFlag, thread A must uncheck from 10 and repeat the search for node 15. In both cases, the key deletion is ultimately successful and without violating the tree structure.

As you can see, the status flags play the role of internal mutexes that provide exclusive access to deleted nodes. It remains to clarify some hints about the admissibility of replacing the CAS primitive with an atomic store when flags are removed, that is, when the node is put into state Clean.

The original algorithm uses mutual assistance (helping) flows when detecting competition on the node. For this, in addition to the status flags, the internal node may contain a handle to the operation being performed - insert or delete. A competing stream, having detected a node state other than Cleanthat, can read the given descriptor and try to help its brother to perform the operation. In this case, the transition to the state Cleanat the end of the operation should be done only by the CAS primitive, since several threads — the initiator of the operation and helpers — can translate the state of the node to Clean. If we make this an atomic store, then a situation is possible when a node transferred to a state Cleanand then to some other subsequent insert / delete operation will be transferred again toCleansome late assistant.

Mutual assistance reception looks good in pseudo-code, but in practice I have not seen much gain from it. Moreover, in C ++, where there is no garbage collector, this technique is quite problematic to implement: it immediately raises the question of how to allocate descriptors (on the stack? Alloc? Pool?), And also more serious - about the lifetime of such a descriptor (reference counting?). In the implementation, libcds helping is disabled: several attempts to implement it were unsuccessful - the code is unstable (this beautiful phrase from the manager’s vocabulary means that the program crashes). So the binary search tree algorithm in libcds contains several artifacts, including CAS instead of the atomic store when translating the state of the node to Clean, which I will get rid of in the future.

Conclusion

This article discusses the algorithm of the simplest binary tree. Despite the lack of balancing, the algorithm is of interest, if only because it is the first step towards the implementation of more complex, self-balancing trees such as AVL-tree and Red-Black tree, which are being worked on, I hope to introduce them to libcds soon.

I would like to end the series of articles on concurrent map with the results of synthetic tests for implementations from libcds (Intel Dual Xeon X5670 2.93 GHz 12 cores 24 threads / 24 GB RAM, average number of elements - 1 million, keys - int):



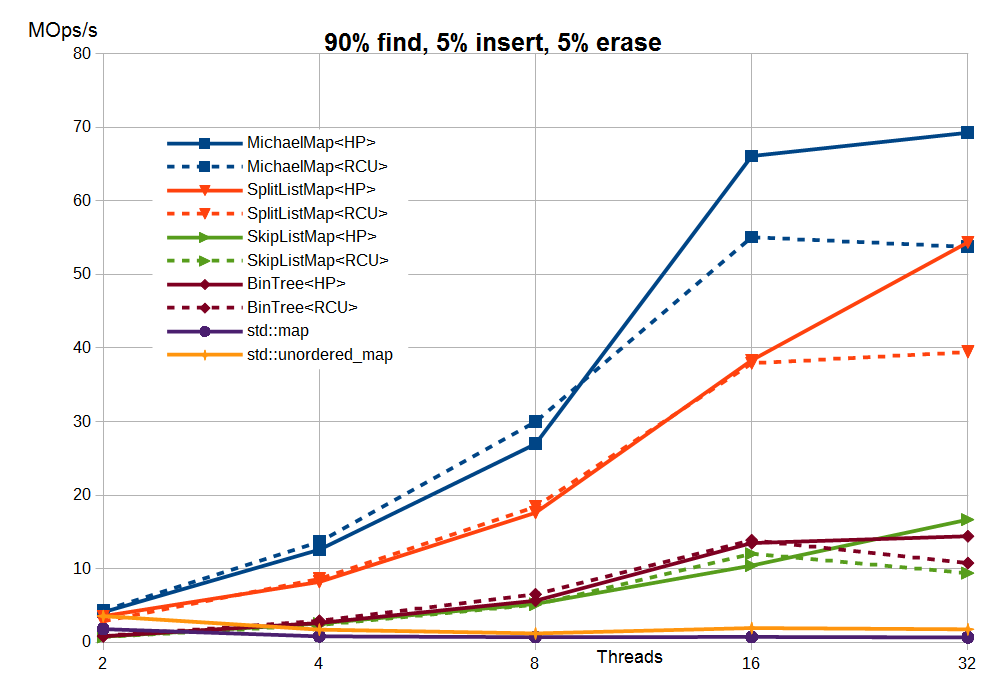
Here:

• MichaelMap is the simplest hash map without rehasing, reviewed here
• SplitListMap - split-ordered list algorithm
• SkipListMap - skip list algorithm
• BinTree - the binary tree discussed in this article
• std :: map, std :: unordered_map - STL algorithms for std :: mutex

The results are shown for Hazard Pointer (HP) and user-space RCU (more precisely, its buffered version cds::urcu::general_buffered).

You can confirm or refute these results by downloading and compiling libcds or applying data structures from libcds in your application.

Perhaps today is all that I would like to talk about lock-free data structures. The end of the epic cycle! There are many questions on lock-free and generally on the internal structure of containers that could be discussed, but they are all very technical and, I am afraid, will not be interesting to the general public.