Analysis of audio analytics algorithms
 The development of Synesis is not limited to video analytics alone. We are also engaged in audio analytics. That's what we wanted to tell you about today. In this article you will learn about the most famous audioanalytical systems, as well as algorithms and their specifics. At the end of the material - traditionally - a list of sources and useful links, including audio libraries.
The development of Synesis is not limited to video analytics alone. We are also engaged in audio analytics. That's what we wanted to tell you about today. In this article you will learn about the most famous audioanalytical systems, as well as algorithms and their specifics. At the end of the material - traditionally - a list of sources and useful links, including audio libraries. Caution: the article can take a long time to load - a lot of pictures.
Author: Mikhail Antonenko.
While video analysis has become a standard feature of many security cameras, built-in audio analytics remains a rather rare phenomenon, despite the presence of both the audio channel in the devices and the available computing power for processing audio data [1]. Nevertheless, audio analytics has some advantages compared to video analytics: the cost of microphones and their maintenance is much cheaper than video cameras; when the system operates in real time, the audio information data stream is much smaller in volume than the data stream from video cameras, which makes more loyal requirements for the bandwidth of the data transmission channel. Audio analytics systems may be especially relevant for urban surveillance, where you can automatically start broadcasting live video to the police console from the place of the explosion and shooting. Audio analytics technologies can also be used to study video recordings and identify events. With increasing awareness of the capabilities of these systems, the use of audio analytics will only expand. Let's start with the basics:
Existing Audio Analytics Solutions
Perhaps the most famous system is ShotSpotter [2], the leader in the United States in detecting firearm shots in urban environments. In the most dangerous areas, directional microphones are installed (on poles, houses, other high buildings) that pick up the sounds of the urban background. In the case of a positive identification of the shot, information with the GPS coordinates of a particular microphone is transmitted to the central computer, where additional sound analysis is carried out to filter out possible false positives, such as a flying helicopter or, for example, an exploding firecracker. If the shot is confirmed, the patrol leaves for the place. The system, installed in Washington in 2006, over the years has localized 39,000 shots from firearms, and the police were able to respond quickly in each case. [3]

Among the providers of audio analytics services in the Russian Federation, “SistemaSarov” can be distinguished [4]. The acoustic monitoring system allows you to automatically select acoustic artifacts in the sound stream, perform their preliminary classification (by type of alarm event), and if the terminal device is equipped with a GPS / GLONASS signal receiver, determine the coordinates of the event and save the events to the archive. [five]
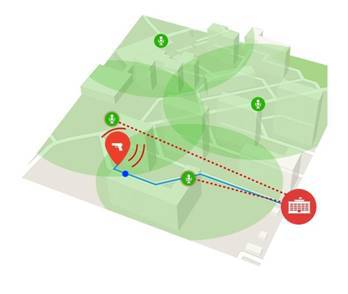
The project “AudioAnalytics” [6], based in the UK, provides several solutions for various use cases. The architecture of the proposed solutions is as follows: the CoreLogger program running on the end-user device allows you to receive and display / save alarm events. It works in conjunction with another part of the overall system - Sound Packs - which is nothing more than a set of different modules of audio analytics. The main features of these modules are the detection of the following audio events:
- aggression (elevated conversation, screaming);
- car alarm;
- breaking glass;
- search for keywords (“police”, “help”, etc.);
- shots;
- screaming / crying baby.
Additionally, a part of the system called Core Trainer is provided, which, based on the set of audio signals submitted to it at the input, will highlight the most different (stand out) parts and form a new pattern for SoundPacks.
Methods and approaches to the detection and recognition of audio events of various types (shot, broken glass, scream)
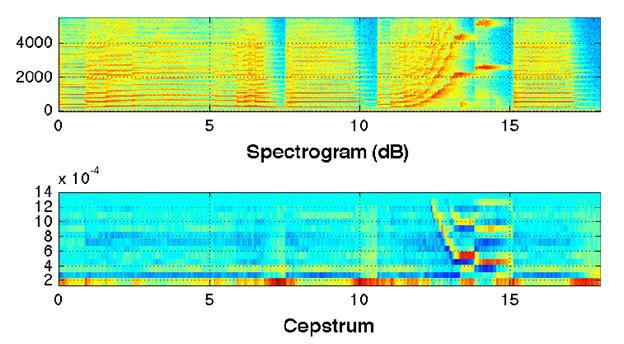
Spectrograms of three different types of audio events are presented as an example of the initial data:
1. A set of shots.

2. Broken glass

3. Scream. The

corresponding audio recordings are downloaded from the audio database [7]. Among other sources of source audio data, the databases [8] [9] [10] [11] can be noted.
The task of recognizing various disturbing audio events is divided into 2 subtasks [12]:
- detection (extraction) of sharp pulse signals from background noise in the audio data stream;
- classification (recognition) of the detected signal to one of the types of audio events.
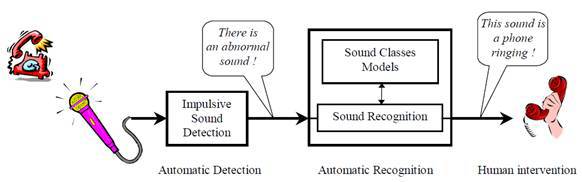
Detection of pulsed eye-catching audio events
Most methods are based on determining the power for a set of consecutive non-overlapping blocks of audio signal [13]. The power for the kth block of the signal, consisting of for N samples, is defined as
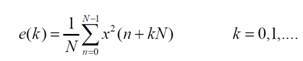
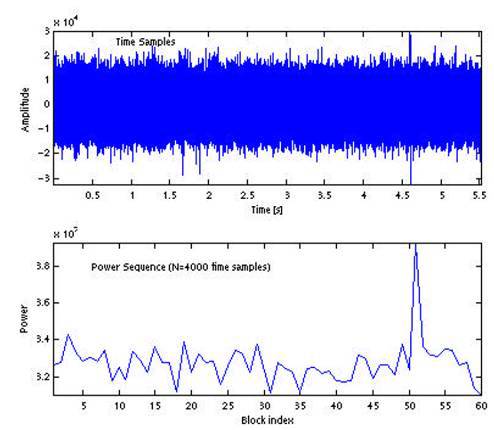
As an example, an audio signal with a shot that occurred at around 4.6 s is given, as well as a set of power values for blocks of N = 4000 samples, which corresponds to a block duration of about 90ms .
Different methods differ in the way they automatically detect a block corresponding to a sharp pulse sound:
based on the standard deviation of the normalized block power values;
based on the use of a median filter for block power values;
by the dynamic threshold for block power values.
Let's look at them in more detail:
A method based on the standard deviation of the normalized block power values
The key aspect of this method is to normalize the considered set of power block values to the range [0, 1]:
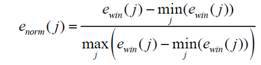
Next, the standard deviation (variance) of the resulting set of values is calculated:

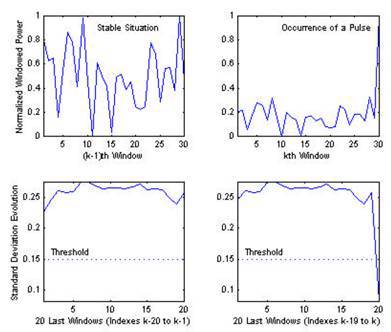
In the case of background noise, the values of the power blocks will be approximately evenly distributed in the range [0-1] (see the figure on the left). Since when a new power value is received for an audio signal block, the values are renormalized to the specified range, when a block with a significantly higher power level occurs, the standard deviation value will significantly decrease compared to the same value for a set of previous background power blocks. By reducing the standard deviation below the threshold value, you can automatically detect a block with a pulse signal.
The advantage of this method is its resistance to changes in noise level, as well as the ability to detect a slowly changing signal by analyzing the average value of normalized power blocks.
Method based on the use of a median filter
The main steps for automatically detecting pulsed outgoing signals using a median filter are presented below. An example of applying a median filter of order k to a set of power block values is shown in the figure below.
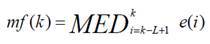
To detect a block with a pulsed event, conditional median filtering is used, which leaves the original signal value if the difference between the initial sample and the median value is less than the threshold value , and the median value otherwise.
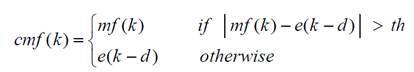
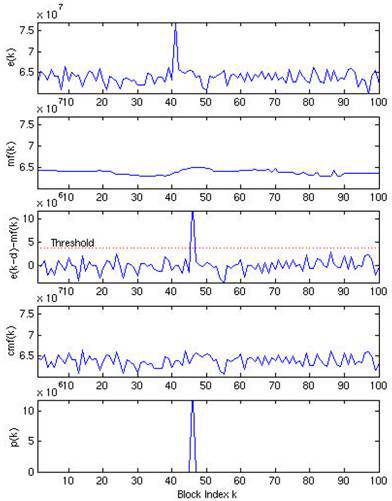
By calculating the difference between the signal after applying the conditional median filter and the shifted original signal, you can automatically select the block with the pulse event.
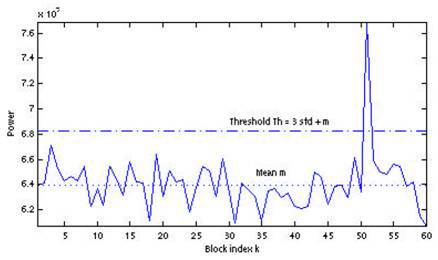
Dynamic Threshold Based Method for Block Power Values
This method proposes to detect a pulsed signal using the average value of the block power set and the standard deviation as the dynamic threshold. Automatic detection occurs when the power of the next block of the threshold value is exceeded, defined as
th = par * std + m
Where par is a parameter that determines the sensitivity of the algorithm. An example of the application of this method with the parameter value par = 3 is presented in the following figure:
Audio Event Recognition
The general scheme of recognition of audio events includes the following stages:
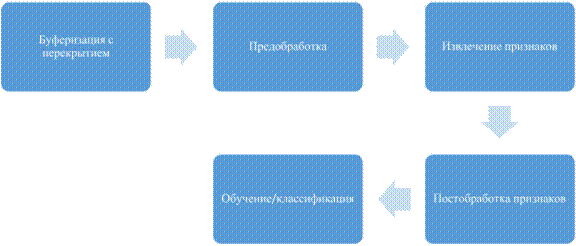
Buffering with overlapping
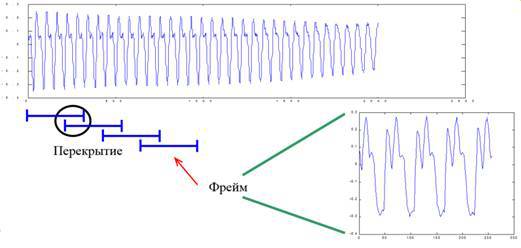
In the first stage, the initial audio signal is converted to a set of frames with overlapping:
The preprocessing
stage The preprocessing stage includes, as a rule, pre-emphasis filtering and window weighing. Pre-emphasis processing is carried out by using an FIR filter H (z) = 1− a / Z. This is necessary for spectral smoothing of the signal [14]. In this case, the signal becomes less susceptible to various noises arising during processing.
Window weighing must be applied due to the fact that the audio frame is time-limited, therefore, when switching to the frequency domain, the side-lobe spectrum will leak out due to the shape of the spectrum function of a rectangular window (it has the form sin (x) / x). Therefore, in order to reduce the effect of this effect, weighting of the initial signal of a different type by windows with a shape other than rectangular is applied. Samples of the input sequence are multiplied by the corresponding function of the window, which entails the zeroing of the signal values at the edges of the sample. The most commonly used functions are the windows of Hamming, Blackman, flat, Kaisel-Bessel, Dolph-Chebyshev [15]. The spectral characteristics of some are listed below: Feature
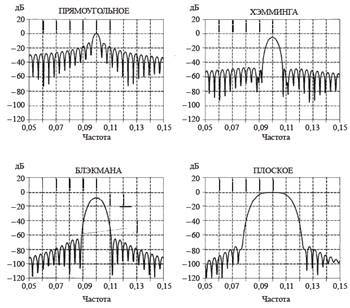
extraction
There are several approaches to extracting descriptors (attributes) from an audio signal. All of them are set by the common goal of reducing signal redundancy and highlighting the most relevant information, and, at the same time, discard irrelevant information. As a rule, features that describe the audio signal from different points of view are combined into one feature vector, on the basis of which the learning process and then classification using the selected trained model are performed. Next will be presented the most popular features allocated from the audio signal.
1. Statistics in the time domain (Time-domain statistics)
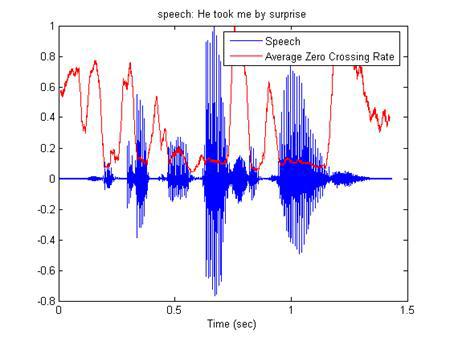
- ZCR (Zero crossing rate) - the number of intersections of the time axis with an audio signal [16].
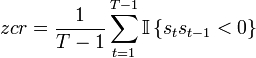
- Short-time energy [17] - average energy value for an audio frame
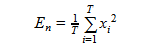
- Entropy of energy [18]
Dividing each frame into a set of sub-frames, the set of energies for each sub-frame is calculated. Further, normalizing the energy of each subframe to the energy of the entire frame, we can consider the energy set as a set of probabilities and calculate the information entropy by the formula:
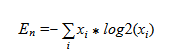
2. Frequency-domain statistic
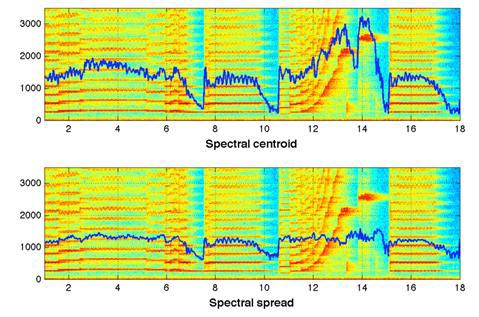
Spectral centroid [17] This
is an interpretation of the “center of mass” spectrum. It is calculated as the sum of the frequencies weighted by the corresponding amplitudes of the spectrum divided by the sum of the amplitudes:

Where F [k] is the amplitude of the spectrum corresponding to the kth frequency value in the DFT spectrum.
Then, the obtained value can be conveniently normalized to the maximum frequency value (Fs / 2), as a result, the range of possible “center of mass” of the spectrum will lie in the range [0-1].
- Spectrum spread [17] (also called instantaneous spectrum width / bandwidth).
It is defined as the second central moment:
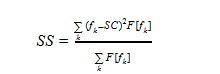
Where fk - frequency values in DFT, F [fk] - amplitude values, SC - Spectral centroid value
- Audio Spectrum Flatness (ASF) [19]
Reflects the deviation of the power of the signal spectrum from a gentle form. From the point of view of human perception, characterizes the degree of tonality of the sound signal.
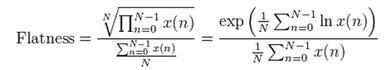
- Energy-band spectrum [20]
The frequency space is divided into N bands, after which the spectrum energy in each band is calculated. The obtained values are taken as signs. In fact, the signs in this case represent the value of the energy of the spectrum in "low resolution".
- Cepstral coefficients
They are obtained on the basis of previous signs by transferring them to the cepstral space. A cepstrum is nothing more than a “spectrum of the logarithm of a spectrum”; instead of the Fourier transform, a discrete cosine transform (DCT) is used:
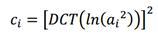
- Spectral entropy
The entropy of the spectrum for a given frame is calculated similarly with the energy entropy in the time domain: the frequency domain of the spectrum is divided into N frequency subdomains, for each of which the part of the total energy of the spectrum attributable to this subdomain is calculated, and then the information entropy is calculated by analogy with the time domain.
- Spectral flux [21]
Spectrum flow - reflects how quickly the energy of the spectrum changes, calculated on the basis of the spectrum on the current and previous frames. It is defined as the second norm (Euclidean distance) between two normalized spectra:
windowFFT = windowFFT / sum (windowFFT);
F = sum ((windowFFT - windowFFTPrev). ^ 2);
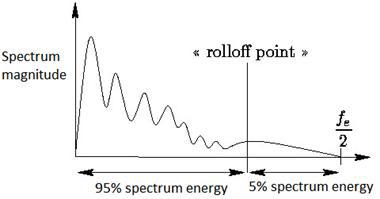
- Spectral rolloff ("blockage" of energy) [22]
It is defined as the relative frequency within which a certain part of the entire spectrum energy is concentrated (set as parameter c):
countFFT -> c * totalEnergy
SR = countFFT / lengthFFT
Spectral rolloff value is shown schematically at c = 0.95:
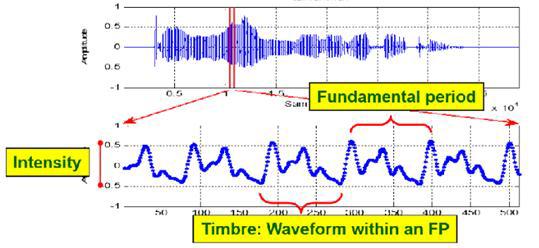
- Signs reflecting the harmony of the audio signal (harmonic ration, fundamental frequency ):
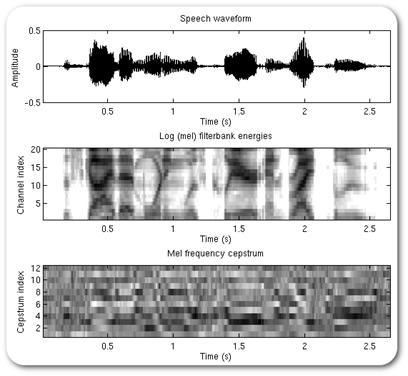
3. MFCC - Mel-frequency cepstral coefficients. (Habra source [23])
The general scheme for obtaining small-frequency cepstral coefficients is presented in the following scheme [24].
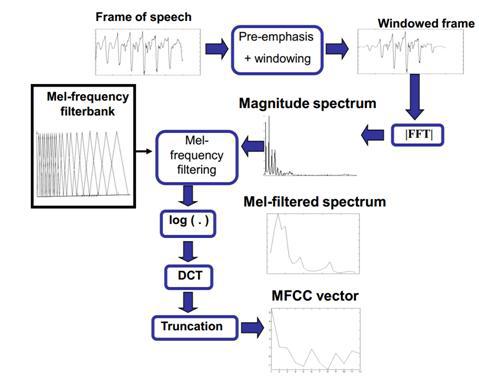
As mentioned earlier, the audio signal is divided into frames, pre-emphasis filtering and window weighing are performed, fast Fourier transform is performed, then the spectrum is passed through a set of triangular filters uniformly located on the chalk scale. This leads to a higher density of filters in the low frequency region and a lower density in the high frequency region, which reflects the sensitivity of perception of sound signals by the human ear. Thus, the basic information is "removed" from the audio signal in the low-frequency region, which is the most relevant feature of audio signals (especially speech). Then the samples are transferred to the cepstral space using the discrete cosine transform (DCT).
Mathematical description:
Apply the Fourier transform to the signal
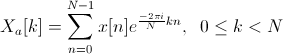
We compose a filter comb using the window function.
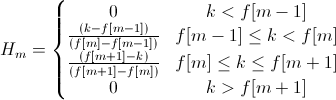
For which the frequencies f [m] are obtained from the equality
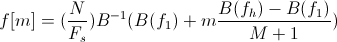
B (b) - conversion of the frequency value to the chalk scale, respectively, We
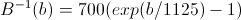
calculate the energy for each window.
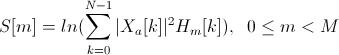
Use DCT

4. LPC (Linear prediction coefficients)
As signs there are coefficients that predict the signal based on a linear combination of previous samples. [25] Essentially, they are FIR filter coefficients of the corresponding order:
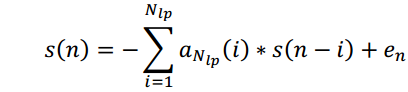
They are also used for speech coding (Linear Prediction Coding), since it is shown that the characteristics of speech signals are well approximated.
Various articles investigate the influence of certain components of the feature vector on the quality of recognition of audio events.
Characteristic Postprocessing
After extracting the necessary signs of the signal for their further use, the signs are normalized so that each component of the feature vector has an average value of 0 and a standard deviation of 1: The mid-term analysis

technique [26] is often used when the averaging of characteristics is performed over a set of consecutive frames. As a rule, 1-10 seconds are selected as the interval for averaging. As a rule, the dimension of the feature vector turns out to be quite large, which significantly affects further the performance of the learning process. That is why in this case, well-known and theoretically studied methods are used to reduce the dimension of the feature vector (LDA, PCA, etc.) [27].

One of the advantages of using dimensional reduction methods is the ability to significantly increase the speed of the learning process by reducing the number of attributes. Moreover, by choosing features that have the best discriminatory abilities in a separate set, it is possible to remove unnecessary irrelevant information, which will increase the accuracy of machine learning algorithms (such as SVM and others) [28]
These methods were mentioned in the face recognition material. The difference between PCA and LDA methods lies in the fact that the PCA method allows to reduce the dimension of the feature vector due to the selection of independent components, which maximally covers the spread in all events.
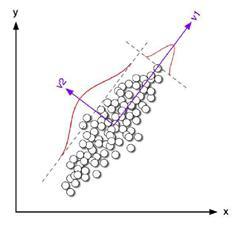
While the LDA identifies the components showing the best discriminatory abilities among a set of classes.
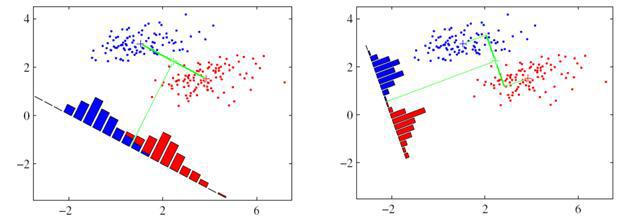
In both the PCA and the LDA, at the training stage, the matrix W is calculated that determines the linear transformation of the original feature vector into a new space of reduced dimension Y = WTX
Classifier selection
Finally, the last step is the selection of a classifier (training model). Some research in the field of audio analytics in the detection of audio signals of interest is devoted to comparing recognition accuracy when using different models of classifiers for various types of audio events. It is noted that the use of hierarchical classifiers significantly increases the accuracy of recognition in comparison with the use of multiclass classifiers. [29] [19]
The simplest version of the recognition model is the Bayesian classifier, which is based on the calculation of the likelihood function for each of the classes, and at the stage of recognition, the event belongs to that class, the posterior probability of which is maximum among all classes. The following figure shows a classification example for a feature vector of dimension 2. Ellipses are centered relative to the average values corresponding to each of the classes, red borders represent a set of feature values, where the classes are equivalent.
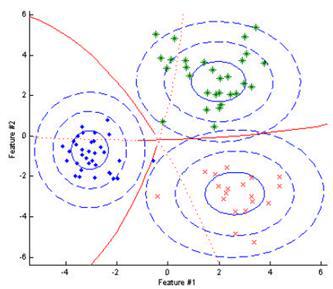
In the case of the selection of signs showing good discriminatory properties, a high recognition result can be achieved using Bayesian classifiers.
Unlike the classical Bayesian classifier, where the parameters of the Gaussian distribution were used to approximate each class, the “mixture” of several Gaussians [19], the parameters of which are selected for each class at the stage, acts as a function of the probability distribution density in the GMM (Gaussian Mixture Model) model learning using EM (Expectation Maximization) algorithm. As can be seen from the figure representing the result of the classification of the three classes, the area of space corresponding to each class is more complex than an ellipse, the recognition model has become more accurate, and accordingly, the recognition result will improve.
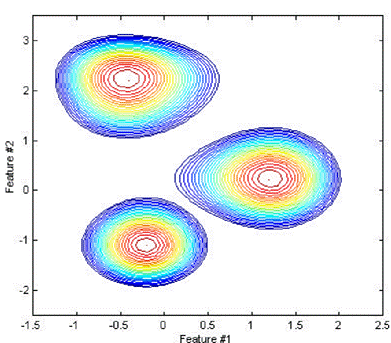
Among the shortcomings of this model, one can note a high sensitivity to variations in the training data sample when choosing a large number of Gaussian distributions, which can lead to a retraining process.
Another way to classify features extracted from an audio signal is the Support Vector Machine (SVM) classifier [30], which translates the original feature vectors into a space with a larger dimension and finds a separating hyperplane as far as possible from the recognized classes. The kernel can be not only a linear function, but also a polynomial function, as well as RBF (radial-basis function) [31].
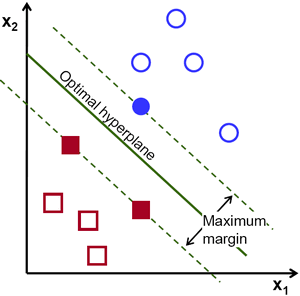
The advantage of this classifier is that at the training stage, the method finds a strip of maximum width, which at the recognition stage will allow for a more accurate classification. Among the disadvantages, one can single out sensitivity to standardization of data and noise.
The use of HMM (Hidden Markov Model) [32] and neural networks [27] as a classifier was considered in our previous review of face recognition algorithms (Habra source [33]).
A page about audio analytics on the company's website .
References
[1] “http://www.secuteck.ru/articles2/videonabl/10-trendov-videonablyudeniya-2014po-versii-kompanii-ihs/,” [On the Internet].
[2] “http://www.shotspotter.com/,” [On the Internet].
[3] “http://habrahabr.ru/post/200850/,” [On the Internet].
[4] “http://sarov-itc.ru/,” [On the Internet].
[5] “http://sarov-itc.ru/docs/acoustic_monitoring_description.pdf,” [On the Internet].
[6] “http://www.audioanalytic.com/,” [On the Internet].
[7] “http://www.freesound.org/,” [On the Internet].
[8] “http://sounds.bl.uk/,” [On the Internet].
[9] “http://www.pdsounds.org/,” [On the Internet].
[10] “http://macaulaylibrary.org/,” [On the Internet].
[11] “http://www.audiomicro.com/,” [On the Internet].
[12] A. Dufaux, “Automatic Sound Detection And Recognition For Noisy Environment.”
[13] IL Freire, “Gunshot detection in noisy environments.”
[14] F. Capman, “Abnormal audio event detection”.
[15] Mikulovich, “Digital Signal Processing,” [On the Internet].
[16] L. Gerosa, “SCREAM AND GUNSHOT DETECTION IN NOISY ENVIRONMENTS”.
[17] C. Clavel, “EVENTS DETECTION FOR AN AUDIO-BASED SURVEILLANCE SYSTEM”.
[18] A. Pikrakis, “GUNSHOT DETECTION IN AUDIO STREAMS FROM MOVIES BY MEANS OF DYNAMIC PROGRAMMING AND BAYESIAN NETWORKS”.
[19] S. Ntalampiras, “ON ACOUSTIC SURVEILLANCE OF HAZARDOUS SITUATIONS”.
[20] MF McKinney, AUTOMATIC SURVEILLANCE OF THE ACOUSTIC ACTIVITY IN OUR LIVING.
[21] D. Conte, “An ensemble of rejecting classifiers for anomaly detection of audio events”.
[22] G. Valenzise, “Scream and Gunshot Detection and Localization for Audio-Surveillance Systems.”
[23] “http://habrahabr.ru/post/140828/,” [On the Internet].
[24] I. Paraskevas, “Feature Extraction for Audio Classification of Gunshots Using the Hartley Transform.”
[25] W. Choi, “Selective Background Adaptation Based Abnormal Acoustic Event Recognition for Audio Surveillance”.
[26] T. Giannakopoulos, “Realtime depression estimation using mid-term audio features,” [Internet].
[27] J. Portˆelo, “NON-SPEECH AUDIO EVENT DETECTION”.
[28] B. Uzkent, “NON-SPEECH ENVIRONMENTAL SOUND CLASSIFICATION USING SVMS WITH A NEW SET OF FEATURES”.
[29] PK Atrey, “AUDIO BASED EVENT DETECTION FOR MULTIMEDIA SURVEILLANCE”.
[30] A. Kumar, “AUDIO EVENT DETECTION FROM ACOUSTIC UNIT OCCURRENCE PATTERNS.”
[31] T. Ahmed, “IMPROVING EFFICIENCY AND RELIABILITY OF GUNSHOT DETECTION SYSTEMS”.
[32] M. Pleva, “Automatic detection of audio events indicating threats”.
[33] “http://habrahabr.ru/company/synesis/blog/238129/,” [On the Internet].
