The math problem of 100 boxes and saving prisoners
I offer readers of "Habrahabr" a translation of the publication "100 Prisoners Escape Puzzle" , which I found on the website of DataGenetics. Please send all errors in this article to private messages.
According to the conditions of the task, there are 100 prisoners in the prison, each of whom has a personal number from 1 to 100. The jailer decides to give the prisoners a chance to be released and offers to pass the test he had invented. If all the prisoners manage, then they are free; if even one fails, everyone will die.

The jailer goes into the secret room and prepares 100 boxes with lids. He puts numbers on each box with numbers from 1 to 100. Then he brings 100 paper plates, according to the number of prisoners, and numbers these plates from 1 to 100. After that he shuffles 100 tablets and puts one plate in each box, closing the lid . The prisoners do not see how the jailer performs all these actions.

The competition begins, the jailer takes each prisoner one by one into the room with boxes and tells the prisoners that they must find the box in which there will be a plate with the number of the prisoner. Prisoners try to find a plate with their number by opening boxes. Each is allowed to open up to 50 boxes; if each prisoner finds his number, the prisoners will be released, if at least one of them does not find his number in 50 attempts, then all prisoners will die.

In order for prisoners to be released, ALL prisoners must pass the test successfully.
So what is the chance that the prisoners will have mercy?
What is the best strategy for prisoners?
At first glance, this task seems almost hopeless. It seems that the chance of each of the prisoners finding their plate is microscopically small. In addition, prisoners cannot exchange information with each other during the trial.
The odds of one prisoner are 50:50. Only 100 boxes and he can open up to 50 boxes in search of his plate. If he will open the boxes at random and open half of all the boxes, he will find his plate in the open half of the boxes, or his plate will remain in closed 50 boxes. His chances of success are ½.

Take two prisoners. If both choose boxes at random, for each of them the odds will be ½, and for two ½x½ = ¼.
(for two prisoners, success will be in one case out of four).
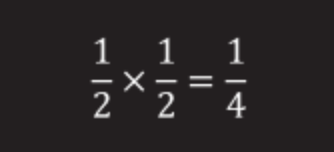
For the three prisoners, the odds will be ½ × ½ × ½ = ⅛.
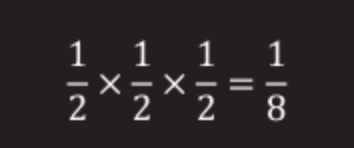
For 100 prisoners, the odds are as follows: ½ × ½ × ... ½ × ½ (multiplying 100 times).
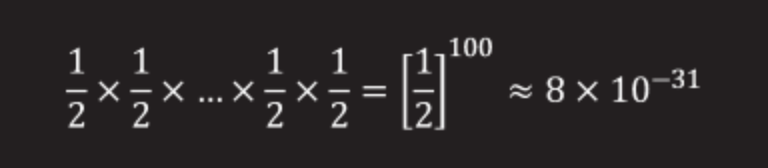
It equals
That is, this is a very small chance. In this situation, most likely, all prisoners will be dead.
It is recommended that you consider this before reading the solution further.
If every prisoner will open boxes at random, then they are unlikely to pass the test. There is a strategy in which prisoners can count on success in more than 30% of cases. This is an incredibly incredible result (if you have not heard about this math problem before).
More than 30% for all 100 prisoners! Yes, this is even more than the chances for two prisoners, provided that they will open the boxes at random. But how is this possible?
It is clear that one in each prisoner the chances cannot be higher than 50% (after all, there is no way for communication between prisoners). But do not forget that the information is stored in the location of the labels inside the boxes. No one shuffles tablets between visits to individual prisoners, so we can use this information.
First I’ll tell you a solution, then I’ll explain why it works.
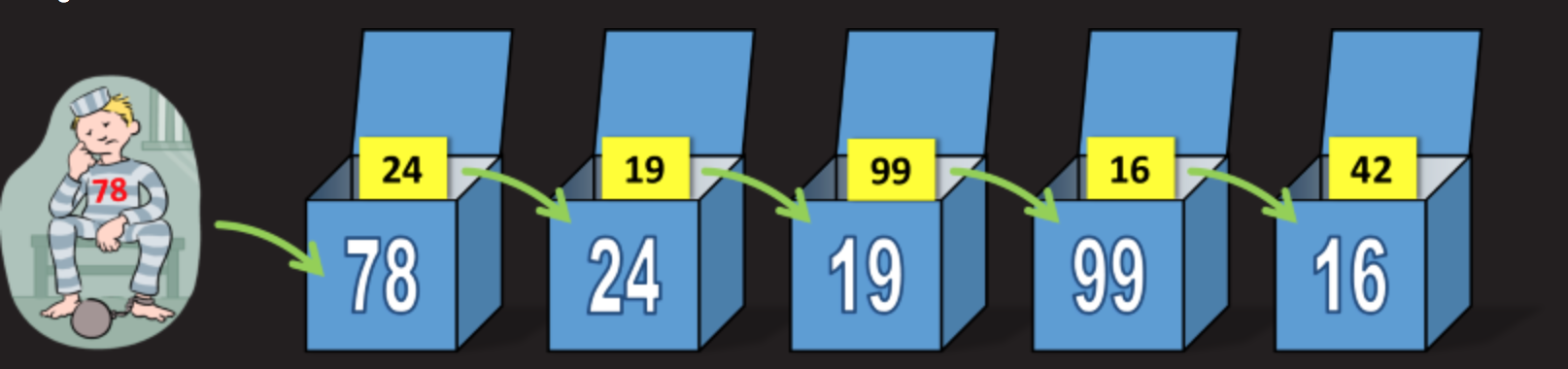
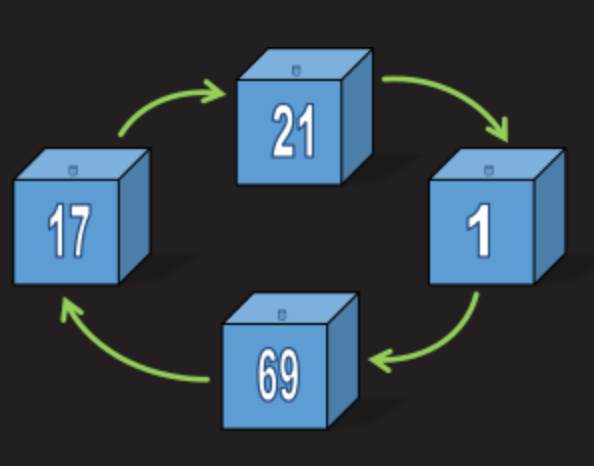
The strategy is extremely easy. The first of the prisoners opens the box with the number that is written on his clothes. For example, prisoner number 78 opens box number 78. If he finds his number on a plate inside the box, then that's great! If not, he looks at the number on the plate in his box and then opens the next box with that number. Opening the second box, he looks at the plate number inside this box and opens the third box with this number. Next, simply transfer this strategy to the remaining boxes. For clarity, see the picture:
In the end, the prisoner will either find his number, or will reach the limit of 50 boxes. At first glance, this looks pointless compared to simply choosing a box at random (and for one individual prisoner it is), but since all 100 prisoners will use the same set of boxes, it makes sense.
Each box has one plate - and this plate is unique. This means that the label is in the box with the same number, or it indicates a different box. Since all plates are unique, there is only one plate for each box pointing to it (and there is only one way to get to this box).

If you think about it, the boxes form a closed round chain. One box can be part of only one chain, because inside the box there is only one pointer to the next and, accordingly, in the previous box there is only one pointer to this box (programmers can see an analogy with linked lists).
If the box does not indicate itself (the number of the box is equal to the number of the plate in it), then it will be in the chain. Some chains may consist of two boxes, some longer.
Since all prisoners start with a box with the same number as on their clothes, they, by definition, get on the chain that contains their plate (there is only one plate that indicates this box).
Exploring the boxes in this chain in a circle, they are guaranteed to eventually find their nameplate.
The only question remains is whether they will find their tablet in 50 moves.
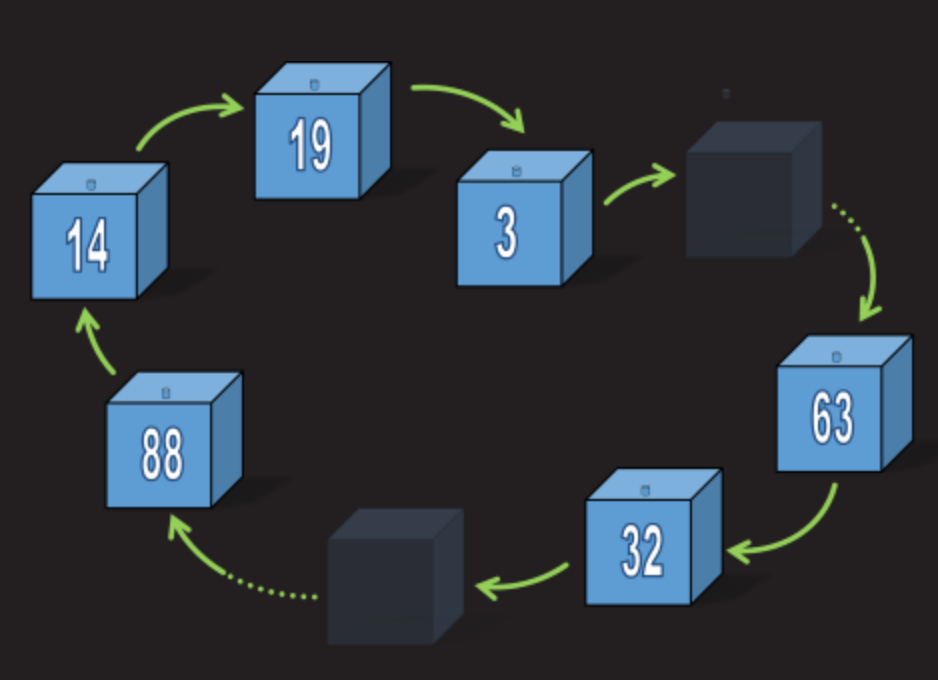
In order for all prisoners to pass the test, the maximum chain length should be less than 50 boxes. If the chain is longer than 50 boxes, prisoners with numbers from these chains will fail the test - and all prisoners will be dead.
Think about it for a second. It turns out that there can only be one chain that is longer than 50 boxes in any layout of labels (we have only 100 boxes, so if one chain is longer than 50, the rest will be shorter than 50 in total).

After you have convinced yourself that to achieve success, the maximum chain length must be less than or equal to 50, and there can be only one long chain in any set, we can calculate the probability of success in passing the test:

So what do we need to figure out the likelihood of a long chain?
For a chain with a length l, the probability that the boxes will be outside this chain is:
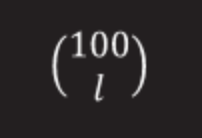
In this collection of numbers there is (l-1)! ways to arrange plates.
The remaining plates may be located (100-l)! ways (do not forget that the length of the chain does not exceed 50).
Given this, the number of permutations that contain a chain of exact length l: (> 50)

It turns out that there are 100 (!) Ways of layouts of labels, so that the probability of a chain of length l is 1 / l. By the way, this result does not depend on the number of boxes.
As we already know, there can be only one option, in which there is a chain of length> 50, so the probability of success is calculated using this formula:
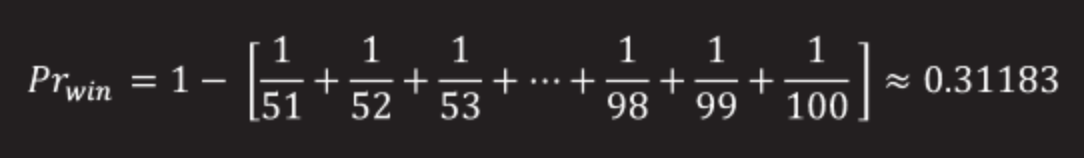
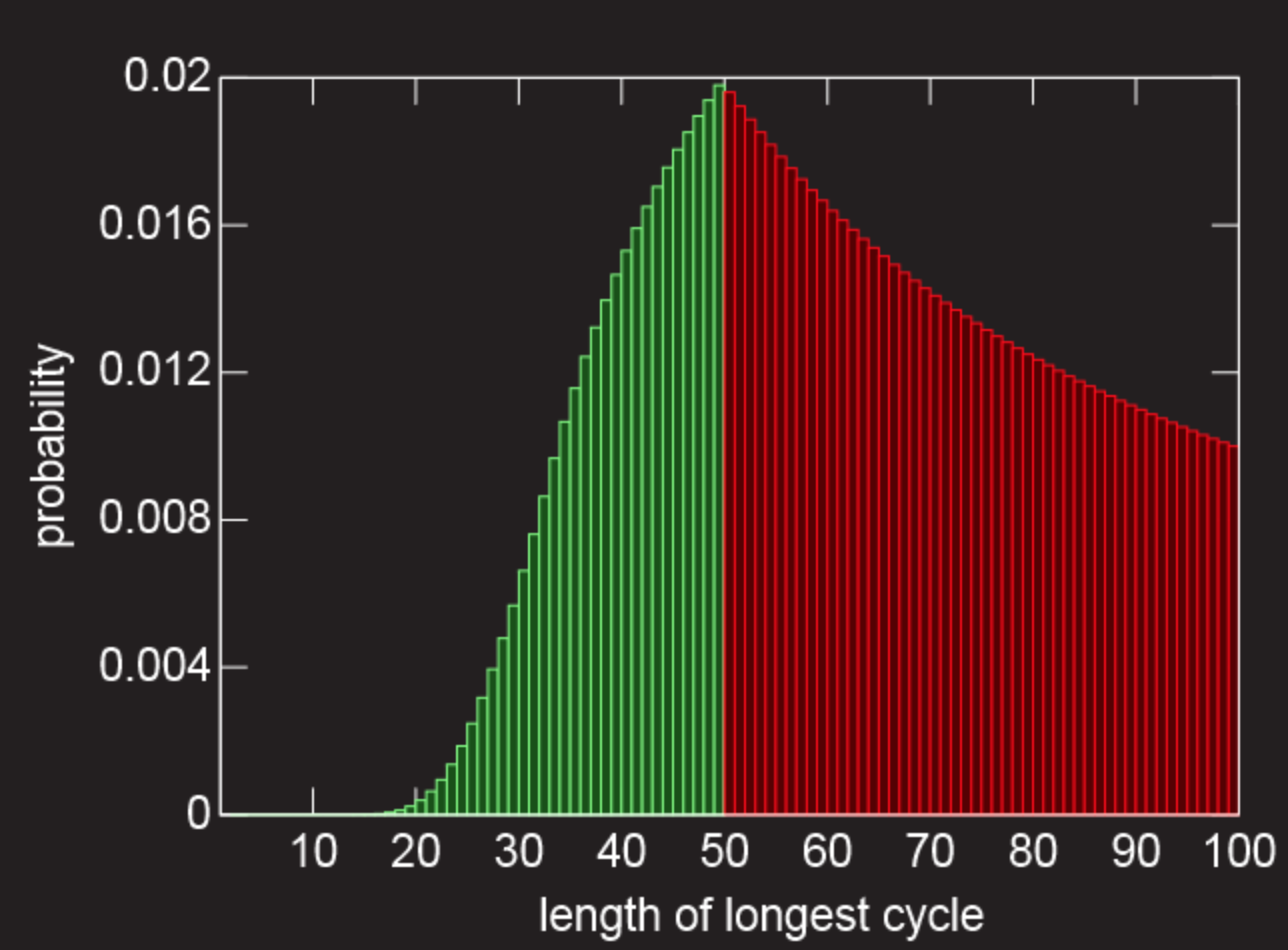
31.18% - the probability that the size of the longest chain will be less than 50 and each of the prisoners will be able to find his own plate, given the limit of 50 attempts.
Below is a graph showing the probabilities (along the ordinate) for all chains of length l (on the abscissa). Red color means all “failures” (this curve here is just a 1 / l graph). Green means “success” (the calculation is a little more complicated for this part of the graph, since there are several ways to determine the maximum length <50). The total probability of the green columns is a 31.18% chance of salvation.
In mathematics, the nth harmonic number is the sum of the reciprocal of the first n consecutive numbers of a natural series.

We can calculate the probability of a jailbreak by adding the corresponding harmonic numbers.
Let's calculate the limit if instead of 100a boxes we have an arbitrary large number of boxes (let's assume that we have 2n boxes in total).
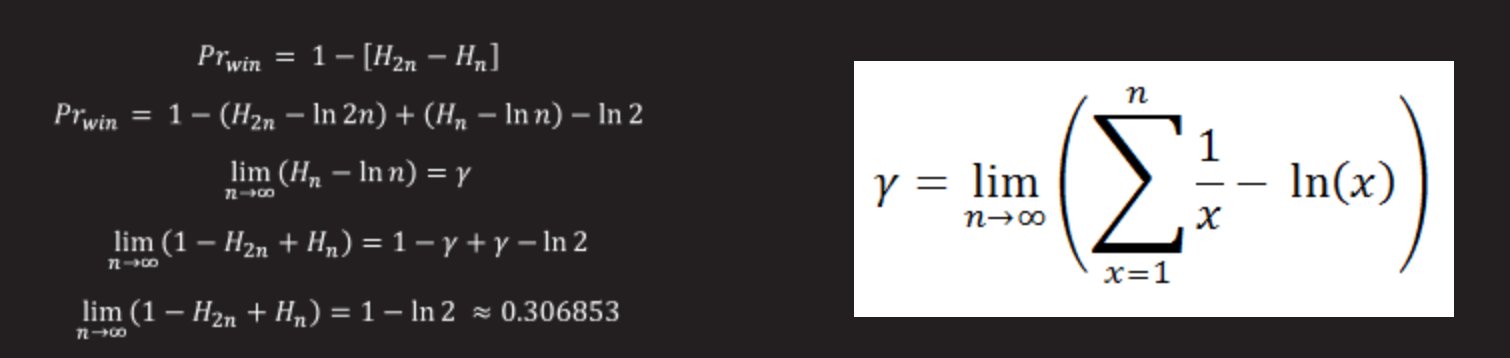
The Euler – Mascheroni constant is a constant defined as the limit of the difference between the partial sum of a harmonic series and the natural logarithm of a number.
(If you made a decision in which prisoners accidentally guess the boxes, then with an increase in the number of prisoners, the probability of salvation tends to zero!)
Does anyone else remember the additional question? What can our helpful comrade do to increase the chances of survival?
Now we already know the solution, so the strategy here is simple: he must examine all the plates and find the longest chain of boxes. If the longest chain is less than 50, then he does not need to change the labels at all, or change them so that the longest chain does not become longer than 50. However, if he finds a chain longer than 50 boxes, all he needs to do is change the contents of two boxes from this chain to break this chain into two shorter chains.
As a result of this strategy, there will be no long chains and all prisoners are guaranteed to find their tablet and salvation. So, by interchanging the two plates, we reduce the probability of salvation to 100%!
According to the conditions of the task, there are 100 prisoners in the prison, each of whom has a personal number from 1 to 100. The jailer decides to give the prisoners a chance to be released and offers to pass the test he had invented. If all the prisoners manage, then they are free; if even one fails, everyone will die.

Task
The jailer goes into the secret room and prepares 100 boxes with lids. He puts numbers on each box with numbers from 1 to 100. Then he brings 100 paper plates, according to the number of prisoners, and numbers these plates from 1 to 100. After that he shuffles 100 tablets and puts one plate in each box, closing the lid . The prisoners do not see how the jailer performs all these actions.

The competition begins, the jailer takes each prisoner one by one into the room with boxes and tells the prisoners that they must find the box in which there will be a plate with the number of the prisoner. Prisoners try to find a plate with their number by opening boxes. Each is allowed to open up to 50 boxes; if each prisoner finds his number, the prisoners will be released, if at least one of them does not find his number in 50 attempts, then all prisoners will die.

In order for prisoners to be released, ALL prisoners must pass the test successfully.
So what is the chance that the prisoners will have mercy?
- After the prisoner opens the box and checks the plate, it is placed back into the box and the lid is closed again;
- Plates cannot be swapped;
- Prisoners cannot give each other clues or somehow interact with each other after the start of the test;
- Prisoners are allowed to discuss the strategy before the test.
What is the best strategy for prisoners?
Additional question:
If a fellow prisoner (not a test participant) will be able to enter the secret room before the test begins, examine all the plates in all the boxes and (optionally, but not necessarily) swap the two plates of the two boxes (in this case, the companion will not have the opportunity to to inform the prisoners about the result of their actions), then what strategy should he take to increase the prisoners' chances of salvation?
Is the solution unlikely?
At first glance, this task seems almost hopeless. It seems that the chance of each of the prisoners finding their plate is microscopically small. In addition, prisoners cannot exchange information with each other during the trial.
The odds of one prisoner are 50:50. Only 100 boxes and he can open up to 50 boxes in search of his plate. If he will open the boxes at random and open half of all the boxes, he will find his plate in the open half of the boxes, or his plate will remain in closed 50 boxes. His chances of success are ½.

Take two prisoners. If both choose boxes at random, for each of them the odds will be ½, and for two ½x½ = ¼.
(for two prisoners, success will be in one case out of four).
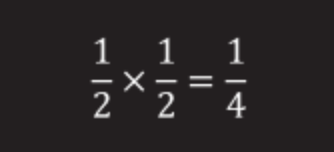
For the three prisoners, the odds will be ½ × ½ × ½ = ⅛.
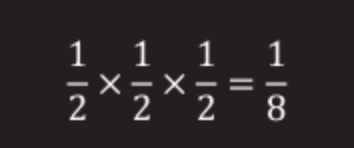
For 100 prisoners, the odds are as follows: ½ × ½ × ... ½ × ½ (multiplying 100 times).
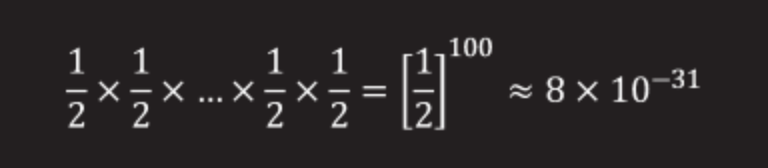
It equals
Pr ≈ 0.0000000000000000000000000000008
That is, this is a very small chance. In this situation, most likely, all prisoners will be dead.
It is recommended that you consider this before reading the solution further.
Incredible answer
If every prisoner will open boxes at random, then they are unlikely to pass the test. There is a strategy in which prisoners can count on success in more than 30% of cases. This is an incredibly incredible result (if you have not heard about this math problem before).
More than 30% for all 100 prisoners! Yes, this is even more than the chances for two prisoners, provided that they will open the boxes at random. But how is this possible?
It is clear that one in each prisoner the chances cannot be higher than 50% (after all, there is no way for communication between prisoners). But do not forget that the information is stored in the location of the labels inside the boxes. No one shuffles tablets between visits to individual prisoners, so we can use this information.
Decision
First I’ll tell you a solution, then I’ll explain why it works.
The strategy is extremely easy. The first of the prisoners opens the box with the number that is written on his clothes. For example, prisoner number 78 opens box number 78. If he finds his number on a plate inside the box, then that's great! If not, he looks at the number on the plate in his box and then opens the next box with that number. Opening the second box, he looks at the plate number inside this box and opens the third box with this number. Next, simply transfer this strategy to the remaining boxes. For clarity, see the picture:

In the end, the prisoner will either find his number, or will reach the limit of 50 boxes. At first glance, this looks pointless compared to simply choosing a box at random (and for one individual prisoner it is), but since all 100 prisoners will use the same set of boxes, it makes sense.
The beauty of this mathematical problem is not only to know the result, but also to understand why this strategy works.
So why does the strategy work?
Each box has one plate - and this plate is unique. This means that the label is in the box with the same number, or it indicates a different box. Since all plates are unique, there is only one plate for each box pointing to it (and there is only one way to get to this box).

If you think about it, the boxes form a closed round chain. One box can be part of only one chain, because inside the box there is only one pointer to the next and, accordingly, in the previous box there is only one pointer to this box (programmers can see an analogy with linked lists).
If the box does not indicate itself (the number of the box is equal to the number of the plate in it), then it will be in the chain. Some chains may consist of two boxes, some longer.

Since all prisoners start with a box with the same number as on their clothes, they, by definition, get on the chain that contains their plate (there is only one plate that indicates this box).
Exploring the boxes in this chain in a circle, they are guaranteed to eventually find their nameplate.
The only question remains is whether they will find their tablet in 50 moves.

Chain length
In order for all prisoners to pass the test, the maximum chain length should be less than 50 boxes. If the chain is longer than 50 boxes, prisoners with numbers from these chains will fail the test - and all prisoners will be dead.
If the maximum length of the longest chain is less than 50 boxes, then all prisoners will pass the test!
Think about it for a second. It turns out that there can only be one chain that is longer than 50 boxes in any layout of labels (we have only 100 boxes, so if one chain is longer than 50, the rest will be shorter than 50 in total).

Long Chance Opportunities
After you have convinced yourself that to achieve success, the maximum chain length must be less than or equal to 50, and there can be only one long chain in any set, we can calculate the probability of success in passing the test:

Some more math
So what do we need to figure out the likelihood of a long chain?
For a chain with a length l, the probability that the boxes will be outside this chain is:
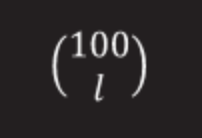
In this collection of numbers there is (l-1)! ways to arrange plates.
The remaining plates may be located (100-l)! ways (do not forget that the length of the chain does not exceed 50).
Given this, the number of permutations that contain a chain of exact length l: (> 50)

It turns out that there are 100 (!) Ways of layouts of labels, so that the probability of a chain of length l is 1 / l. By the way, this result does not depend on the number of boxes.
As we already know, there can be only one option, in which there is a chain of length> 50, so the probability of success is calculated using this formula:
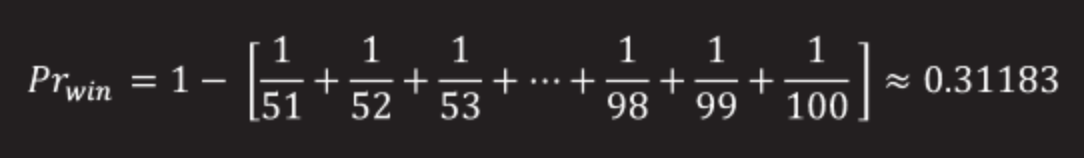
Result
31.18% - the probability that the size of the longest chain will be less than 50 and each of the prisoners will be able to find his own plate, given the limit of 50 attempts.
The likelihood that all prisoners will find their tablets and pass the test 31.18%
Below is a graph showing the probabilities (along the ordinate) for all chains of length l (on the abscissa). Red color means all “failures” (this curve here is just a 1 / l graph). Green means “success” (the calculation is a little more complicated for this part of the graph, since there are several ways to determine the maximum length <50). The total probability of the green columns is a 31.18% chance of salvation.

Harmonic number (this part of the article is for geeks)
In mathematics, the nth harmonic number is the sum of the reciprocal of the first n consecutive numbers of a natural series.

We can calculate the probability of a jailbreak by adding the corresponding harmonic numbers.
Let's calculate the limit if instead of 100a boxes we have an arbitrary large number of boxes (let's assume that we have 2n boxes in total).
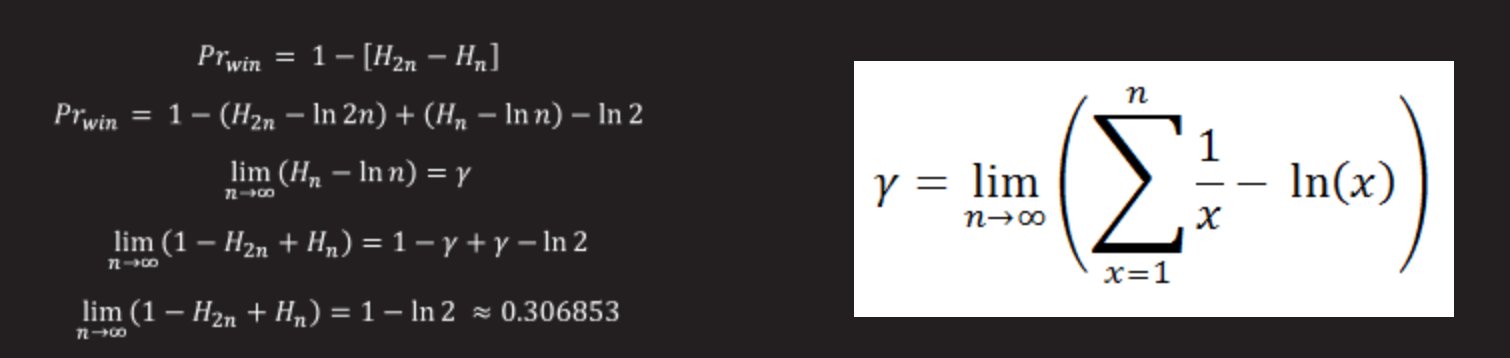
The Euler – Mascheroni constant is a constant defined as the limit of the difference between the partial sum of a harmonic series and the natural logarithm of a number.
As the number of prisoners increases, provided that the overseer allows prisoners to open half of all the boxes, the chance of salvation tends to the number 30.685%
(If you made a decision in which prisoners accidentally guess the boxes, then with an increase in the number of prisoners, the probability of salvation tends to zero!)
Additional question
Does anyone else remember the additional question? What can our helpful comrade do to increase the chances of survival?
Now we already know the solution, so the strategy here is simple: he must examine all the plates and find the longest chain of boxes. If the longest chain is less than 50, then he does not need to change the labels at all, or change them so that the longest chain does not become longer than 50. However, if he finds a chain longer than 50 boxes, all he needs to do is change the contents of two boxes from this chain to break this chain into two shorter chains.
As a result of this strategy, there will be no long chains and all prisoners are guaranteed to find their tablet and salvation. So, by interchanging the two plates, we reduce the probability of salvation to 100%!
