January 27, 2015 at 13:21Finance in Excel + VBA. Black Scholes Options Options Calculator
The article is addressed and will be useful primarily to those who have begun to study options and want to understand their pricing. And secondly, for those who have not yet used the VBA tool in their calculations in Excel, but want to learn - you will see how simple it is.
To begin with briefly on the nature and pricing of options. An option has four main parameters:
1. Underlying asset
2. Type of option (Call or Put)
3. Strike price ( strike price of the option)
4. Expiration date (expiration) of the option
For the option buyer, it represents the right to buy (Call option) or sell (Put option) underlying asset at strike price on expiration day. For an option seller, it is an obligationsell (Call option) or buy (Put option) underlying asset at a strike price on the day of expiration. In fact, the option is insurance against changes in the price of the underlying asset (BA) from the time of the transaction to the expiration date - the seller acts as the insurer (in the event of an unfavorable change in the price of the BA, he pays insurance to the buyer of the option), and the policyholder is the buyer of the option (he pays insurance to the seller )
Like the price of insurance, the option price is completely determined by the probability of an “insured event”, i.e. exercise of the option (exercise of the right of the buyer of the option). The main components that affect this probability and the option price, the cost of insurance that the buyer pays and the seller receives:
Moreover, the dependence of the option price for each of these three components is nonlinear . The generally accepted option pricing formula for these key factors was developed by Fisher Black and Myron Scholes in 1973.
The Black-Scholes formula is as follows (see Wikipedia for details):
Price of the (European) call option:
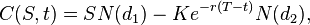
Price of the (European) put option:
Designations:
C (S, t) - the current value of the call option at time t before the expiration of the option ( before expiration);
S is the current price of the underlying asset;
N (x)- the likelihood that the deviation will be less under the conditions of the standard normal distribution (thus, they limit the range of values for the standard normal distribution function);
K is the exercise price of the option;
r - risk-free interest rate;
T - t - time until the expiration of the option;
- yield volatility (the square root of the variance) of the underlying asset.
To assess the sensitivity of the option price to the BA price, volatility, and the time to expiration, coefficients called Greeks are used (coefficients are mainly denoted by Greek letters, with the exception of “vegi”).
The Greeks in the Black-Scholes model are calculated as follows:
1. Delta (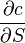
) - the rate of change of the option price from a change in the BA price. For a call option, the delta is equal to 
, for a put option 
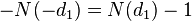. Delta shows the current slope of the option value curve depending on the price of the BA.
2. Gamma (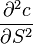
) - the rate of change of the option price from a change in the Delta (or acceleration from a change in the price of the BA). Gamma is equal 
.
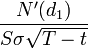3. Vega (
) - describes the dependence of the price of the option changes from asthma volatility 
. Vega reflects the number of points in the option value changing for each percentage point (1%) of the volatility change.
4. Theta (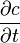
) - describes the option price reduction depending on the time before expiration. For Call - 
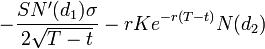, for Put - 
.
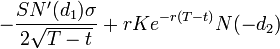The above formulas are true for the general case, including the case of stock options. For calculating options on futures contracts, the risk-free rate r is not applied. Because Options on futures are traded on the Moscow Exchange, then we do not take into account the interest rate in the calculations.
So, the implementation of the Black-Scholes model in Excel + VBA.
For convenience, we will create a function for each variable from the BS model. Each function will have input variables:
S - BA price
X - strike price
d - number of days before expiration
y - number of days in a year
v -
OptionType volatility - option type “Call” or “Put” (only for calculating price and delta)
Record A regular function in VBA is as follows:
Such a function can be called from other functions or from an Excel worksheet.
Functions are written to the created Module (run VBA in Excel, for example, by pressing Alt + F11, select Insert -> Module):
The finished Excel file can be downloaded from the link .
Now in the Excel cell we can call any function that we have prescribed, for example, by entering = OptionPrice (“Put”; 76870; 90,000; 13; 365; 0.47) in the cell, we get the theoretical price of the Put option with the price of the underlying asset 76870, strike 90,000, estimated volatility 45 % and 13 days before expiration.
So, we got a working option calculator on VBA, which can be used both to study the properties of options (to build diagrams of price and Greek dependencies on different market parameters), and used to trade and build more complex programs.
Options Basics
To begin with briefly on the nature and pricing of options. An option has four main parameters:
1. Underlying asset
2. Type of option (Call or Put)
3. Strike price ( strike price of the option)
4. Expiration date (expiration) of the option
For the option buyer, it represents the right to buy (Call option) or sell (Put option) underlying asset at strike price on expiration day. For an option seller, it is an obligationsell (Call option) or buy (Put option) underlying asset at a strike price on the day of expiration. In fact, the option is insurance against changes in the price of the underlying asset (BA) from the time of the transaction to the expiration date - the seller acts as the insurer (in the event of an unfavorable change in the price of the BA, he pays insurance to the buyer of the option), and the policyholder is the buyer of the option (he pays insurance to the seller )
Like the price of insurance, the option price is completely determined by the probability of an “insured event”, i.e. exercise of the option (exercise of the right of the buyer of the option). The main components that affect this probability and the option price, the cost of insurance that the buyer pays and the seller receives:
- The difference between the strike price and the price of the underlying asset . Those. when buying a Call, the higher its strike, the cheaper it is (since the probability that the BA will be higher than the strike price at the time of expiration)
- Base asset volatility . The higher the volatility (roughly the range of price fluctuations) of the BA, the higher the probability of reaching a strike before expiration.
- Time to expiration . The more time before the expiration of an option, the higher the probability that when buying a Call the price of the underlying asset will go above the strike, so the option price is higher.
Moreover, the dependence of the option price for each of these three components is nonlinear . The generally accepted option pricing formula for these key factors was developed by Fisher Black and Myron Scholes in 1973.
The Black-Scholes formula is as follows (see Wikipedia for details):
Price of the (European) call option:
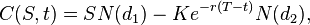
Price of the (European) put option:
Designations:
C (S, t) - the current value of the call option at time t before the expiration of the option ( before expiration);
S is the current price of the underlying asset;
N (x)- the likelihood that the deviation will be less under the conditions of the standard normal distribution (thus, they limit the range of values for the standard normal distribution function);
K is the exercise price of the option;
r - risk-free interest rate;
T - t - time until the expiration of the option;
- yield volatility (the square root of the variance) of the underlying asset.Greeks options
To assess the sensitivity of the option price to the BA price, volatility, and the time to expiration, coefficients called Greeks are used (coefficients are mainly denoted by Greek letters, with the exception of “vegi”).
The Greeks in the Black-Scholes model are calculated as follows:
1. Delta (
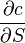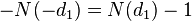) - the rate of change of the option price from a change in the BA price. For a call option, the delta is equal to , for a put option . Delta shows the current slope of the option value curve depending on the price of the BA. 2. Gamma (
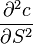) - the rate of change of the option price from a change in the Delta (or acceleration from a change in the price of the BA). Gamma is equal 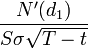. 3. Vega (
) - describes the dependence of the price of the option changes from asthma volatility . Vega reflects the number of points in the option value changing for each percentage point (1%) of the volatility change. 4. Theta (
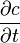) - describes the option price reduction depending on the time before expiration. For Call - 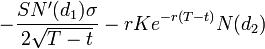, for Put - 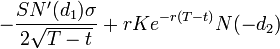. The above formulas are true for the general case, including the case of stock options. For calculating options on futures contracts, the risk-free rate r is not applied. Because Options on futures are traded on the Moscow Exchange, then we do not take into account the interest rate in the calculations.
Model implementation in MS Excel
So, the implementation of the Black-Scholes model in Excel + VBA.
For convenience, we will create a function for each variable from the BS model. Each function will have input variables:
S - BA price
X - strike price
d - number of days before expiration
y - number of days in a year
v -
OptionType volatility - option type “Call” or “Put” (only for calculating price and delta)
Record A regular function in VBA is as follows:
Function Function Name (comma separated input variables)
... calculations ... Function
Name = ... calculations ...
End Function
Such a function can be called from other functions or from an Excel worksheet.
Functions are written to the created Module (run VBA in Excel, for example, by pressing Alt + F11, select Insert -> Module):
Function d_1 (S, X, d, y, v)
T = d / y
d_1 = (Log (S / X) + (0.5 * (v ^ 2)) * T) / (v * (T ^ 0.5))
End Function
Function d_2 (S, X, d, y, v)
T = d / y
d_2 = d_1 (S, X, d, y, v) - v * (T ^ 0.5)
End Function
Function Nd_1 (S, X , d, y, v)
Nd_1 = Application.NormSDist (d_1 (S, X, d, y, v))
End Function
Function Nd_2 (S, X, d, y, v)
Nd_2 = Application.NormSDist (d_2 (S , X, d, y, v))
End Function
Function N_d_1 (S, X, d, y, v)
N_d_1 = Application.NormSDist (-d_1 (S, X, d, y, v))
End Function
Function N_d_2 ( S, X, d, y, v)
N_d_2 = Application.NormSDist (-d_2 (S, X, d, y, v))
End Function
Function N1d_1 (S, X, d, y, v)
T = d / y
N1d_1 = 1 / (2 * Application.Pi ()) ^ 0.5 * (Exp (-0.5 * d_1 (S, X, d, y, v) ^ 2))
End Function
Function OptionPrice (OptionType, S, X, d, y, v)
If OptionType = “Call” Then
OptionPrice = S * Nd_1 (S, X, d, y, v) - X * Nd_2 (S, X, d, y, v)
ElseIf OptionType = “Put” Then
OptionPrice = X * N_d_2 (S, X, d, y, v) - S * N_d_1 (S, X, d, y, v)
End If
End Function
Function Delta (OptionType, S, X, d, y, v)
If OptionType = "Call" Then
Delta = Application.NormSDist (d_1 (S, X, d, y, v))
ElseIf OptionType = "Put" Then
Delta = Application.NormSDist (d_1 (S, X, d, y, v)) - 1
End If
End Function
Function Theta (S, X, d, y, v)
T = d / y
Theta = - ((S * v * N1d_1 (S, X, d, y, v)) / (2 * (T ^ 0.5)) ) / y
End Function
Function Gamma (S, X, d, y, v)
T = d / y
Gamma = N1d_1 (S, X, d, y, v) / (S * (v * (T ^ 0.5)) )
End Function
Function Vega (S, X, d, y, v)
T = d / y
Vega = (S * (T ^ 0.5) * N1d_1 (S, X, d, y, v)) / 100
End Function
The finished Excel file can be downloaded from the link .
Now in the Excel cell we can call any function that we have prescribed, for example, by entering = OptionPrice (“Put”; 76870; 90,000; 13; 365; 0.47) in the cell, we get the theoretical price of the Put option with the price of the underlying asset 76870, strike 90,000, estimated volatility 45 % and 13 days before expiration.
Some points that I would like to note
- The theoretical values obtained in our program are almost identical to those transmitted by the Mosbirzha, which means that the exchange uses the BS model in its calculations.
- In fact, the option (like insurance) does not have a true fair value - it is for everyone its own, and it depends on what kind of volatility is supposed or how to take into account the number of days (take into account weekends, how much weight to take into account different days of the week, how many days a year use in formula) etc.
- The Greeks have a wonderful property - to get the value of the Greeks for the portfolio of futures and options, you just need to add the corresponding Greeks for the individual assets of the portfolio. Those. we can easily calculate, for example, how much you need to buy / sell basic futures so that the total portfolio value does not change when the price of this futures changes (the so-called Delta alignment or delta hedging).
- Despite its prevalence, the BS model is based on the assumption that the return on the asset has a normal distribution, which is never performed in the real market.
Total
So, we got a working option calculator on VBA, which can be used both to study the properties of options (to build diagrams of price and Greek dependencies on different market parameters), and used to trade and build more complex programs.