saluev January 27, 2015 at 02:16

C ++ 11 variadic templates and long arithmetic at compile time

Tutorial

In the thirty years that have passed since its appearance in the bowels of Bell Labs, C ++ has come a long way, going from "advanced C" to one of the most popular and expressive compiled languages. Especially a lot, in the author’s purely personal view, gave C ++ the new C ++ 11 standard, which is rapidly gaining compiler support. In this article, we will try to “touch with our hands” one of its most powerful features - templates with a variable number of arguments ( variadic templates ).

Developers familiar with Alexandrescu books probably remember the concept of a type list. In the good old C ++ 03, if you need to use an unknown number of template arguments in advance, it was suggested to create such a list and then use it with a cunning hack. Tuples (now std :: tuple) and so on were implemented in this way. and so on. And the chapter on type lists itself made it clear that practically any kind of calculations can be done on C ++ templates (doing λ-calculus , for example), if only they could be written in a functional style. The same concept could be applied to long arithmetic: store long numbers as lists of ints, introduce a main class of the form

template struct BigInteger { };

, operations on him and so on. But to the glory of the new standard, we will go the other way.

Parameter packs

So, the foundation is the new syntax introduced in C ++ 11. First, let's look at what the definition of the tuple class should look like, which is not a crime against humanity:

template
class tuple {
    // ...
};

Note the ellipsis in the template arguments. Now Types - not a type name, but parameter pack - a collection of zero or more arbitrary types. How to use it? Cunningly.

The first way: as a set of argument types of functions or methods. This is done like this:

template
void just_do_nothing_for_no_reason(Types... args) {
    // indeed
}

Here Types... args is another special syntax construct ( function parameter pack ), which is expanded into the corresponding argument pack of the function argument chain. Since C ++ supports auto-detection of arguments to template functions, this function of ours can now be called with any number of arguments of any type.

Well, then what? What can you do with all these arguments ?

Firstly, you can simply use it further, as types of other functions or templates with a variable number of arguments:

template
tuple make_tuple(Types... args) {
    tuple result(args...);
    return result;
}

Types... argswe already know. args... - Another special construction ( parameter pack expansion ), which in this case will expand into a list of function arguments, separated by a comma. So, if you put a call somewhere in the code make_tuple(1, 1.f, '1'), a function of the form will be created and called

tuple make_tuple(int a1, float a2, char a3) {
    tuple result(a1, a2, a3);
    return result;
}

Secondly, it can be used in more complex transformations. In fact, parameter pack expansion supports more than just comma-delimited anything and everything. So, you can easily implement the following function:

template
std::tuple just_double_everything(Types... args) {
    std::tuple result((args * 2)...); // OMG
    return result;
}

IIIii - yes, you guessed it! The design ((args * 2)...)will unfold in (a1 * 2, a2 * 2, a3 * 2).

And finally, thirdly (and in the most common ones), argument lists can be used in recursion:

template
std::ostream& print(std::ostream& where, const T& what) {
    return where << what;
}
template
std::ostream& print(std::ostream& where, const T& what, const Types& ... other) {
    return print(where << what << ' ', other...);
}

The output is a type-safe printf - definitely worth it!

Using a certain amount of template magic, you can learn how to extract type and value from packs by number and perform other frauds. Example under the spoiler.

Listing Tuples

template
struct seq { };   // просто статический список чисел
template // генератор списка по типу Python'овского range()
struct make_range : make_range { };
template
struct make_range<0, S...> {
  typedef seq result;
};
template
std::ostream& operator_shl_impl(
        std::ostream& out,
        const std::tuple& what,
        const seq /* a dummy argument */ ) {
    return print(out, std::get(what)...);
}
template
std::ostream& operator<<(std::ostream& out, const std::tuple& what) {
    using range = typename make_range::result;
    return operator_shl_impl(out, what, range());
}

Here we see a command that has not yet been mentioned, but is quite simple to understand sizeof...(Types) - it returns the number of types in the parameter pack. By the way, it can be implemented independently.

So, the whole point in the line

print(out, std::get(what)...);

It does nothing more than call a function with arguments from a tuple . Just think! It was for this focus that we needed a list of numbers from 0 to (n - 1) - it is thanks to him that this line unfolds into something like

print(out, std::get<0>(what), std::get<1>(what), std::get<2>(what));

Write a list generator from (n - 1) to 0 - and you can expand the tuples with one line:

auto reversed_tuple = std::make_tuple(std::get(my_tuple)...);

Morality: pack expansion is a killer tool.

Long arithmetic

Let's start our implementation of long arithmetic. First, we define the main class:

template
struct BigUnsigned {
    static const size_t length = sizeof...(digits); // количество аргументов
};
using Zero = BigUnsigned< >;
using One  = BigUnsigned<1>;

In the best traditions of computing at the compilation stage in C ++, all, in fact, the data here is not stored anywhere, but are the direct arguments of the template. C ++ will distinguish between BigUnsigned class implementations with different sets of parameters, due to which we can implement our calculations. We agree that the first parameter will contain the lower 32 bits of our long number, and the last one will contain the most significant 32, including possibly leading zeros (I personally see this as the most logical solution).

Before we do the implementation of addition, let's define the concatenation operation on our long numbers. Using this operation as an example, we will introduce standard tactics that we will use in the future.

So, we define an operation on two types:

template
struct Concatenate {
    using Result = void;
};

We mean that these two types will be BigUnsigned implementations. We realize the operation for them:

template
struct Concatenate, BigUnsigned> { // >> - не проблема для C++11
    using Result = BigUnsigned; // да! просто перечислим их подряд!
};

It is no less trivial to implement bitwise operations, for example, (very naive) xor:

template struct Xor;
template
struct Xor, BigUnsigned> {
    using Result = BigUnsigned< (a^b)... >; // будет работать, но только когда длина a и b совпадает
};

Now, actually, addition. There is no getting around - you have to use recursion. Define the main class and recursion base:

template struct Sum;
template struct Sum { using Result = A;    };
template struct Sum<   A, Zero> { using Result = A;    };
// если не определить этот частный случай отдельно, компилятор будет колебаться между предыдущими двумя:
template<       > struct Sum { using Result = Zero; };

Now for the basic calculations:

template
struct Sum, BigUnsigned> {
    static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0;
    using Result = typename Concatenate<
        BigUnsigned,
        typename Sum<
            typename Sum<
                BigUnsigned, BigUnsigned
            >::Result,
            BigUnsigned
        >::Result
    >::Result;
};

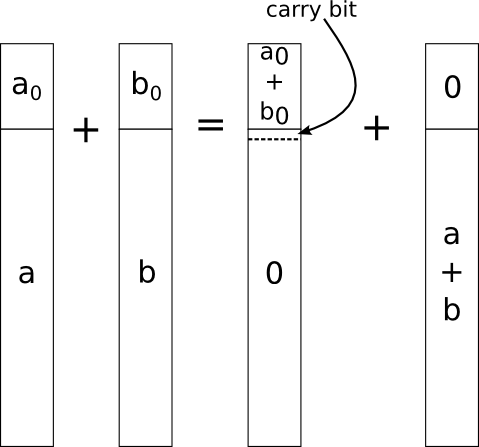
So what happened.

View Template

template
struct Sum, BigUnsigned> {

we need to separate the least significant bits of long numbers from all the most significant. If we used a more general template

template
struct Sum, BigUnsigned> {

, then it would not be so easy to do this and we would need a few more auxiliary structures. (But one could write them wisely and subsequently realize the multiplication of Karatsuba, nya!)

Next, the line

    static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0;

computes the so-called carry bit, indicating whether overflow occurred in the current bit or not. (Instead of a constant, UINT32_MAXyou can and should use std :: numeric_limits .)

Finally, the final calculation finds the result using recursion according to the rule

Well, you can test! The actual calculations will look something like this:

using A = BigUnsigned<0xFFFFFFFFFFFFFFFFULL>;
using B = One;
using C = Sum::Result;
int main(int argc, char** argv) {
    // ...
}

Compiled! Launched! But ... how do you know the meaning of C? How, actually, to test something?

The easy way: let's throw an error at the compilation stage. For example, write in main

int main(int argc, char** argv) {
    C::entertain_me();
}

When trying to compile such a code, we get a logical error:

static_bignum.cpp: В функции «int main(int, char**)»:
static_bignum.cpp:32:5: ошибка: «entertain_me» не является элементом «C {aka static_bignum::BigUnsigned<0, 1>}»
     C::entertain_me();
     ^

However, with this whining about the error g ++ gave us the main secret - now we see that C is equal static_bignum::BigUnsigned<0, 1>, that is 2 ³² - everything came together!

A less simple way: let's write a function that will generate a string with a binary representation of a given number. The blank will look something like this:

template struct BinaryRepresentation;
template
struct BinaryRepresentation> {
    static std::string str(void) {
        // ...
    }
};

We will use the standard std :: bitset object to print the current 32 bits at each stage:

template struct BinaryRepresentation;
template
struct BinaryRepresentation> {
    static std::string str(void) {
        std::bitset<32> bset(a_0);
        return BinaryRepresentation>::str() + bset.to_string();
    }
};

It remains only to set the recursion base:

template<>
struct BinaryRepresentation {
    static std::string str(void) {
        return "0b"; // Oppa Python Style
    }
};

The new version of our primitive test will look like

using A = BigUnsigned<0xFFFFFFFFFFFFFFFFULL>;
using B = One;
using C = Sum::Result;
int main(int argc, char** argv) {
    std::cout << BinaryRepresentation::str() << std::endl;
}

and will give us a simply amazing answer with its readability

0b00000000000000000000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000000000000

However, by carefully counting the number of zeros, you can make sure that this is still 2 ³² !

A complex, but the most convincing way - the derivation of the decimal notation - will require us to do some work, namely the implementation of the division operation.

For this we need certain, um, prerequisites.

Subtraction Implementation

template
struct Difference;
struct OverflowError {}; // класс-индикатор ошибки (вычли большее число из меньшего)
// вычитание нуля из нуля -- ну эт мы умеем:
template<> struct Difference { using Result = Zero; };
template // вычитание нуля -- довольно просто
struct Difference, Zero> { using Result = BigUnsigned; };
template // вычитание из нуля -- довольно однозначно
struct Difference> { using Result = OverflowError; };
template struct Difference { using Result = OverflowError; };
template struct Difference { using Result = OverflowError; };
template
struct Difference, BigUnsigned > {
    using A = BigUnsigned; // вводим короткие имена для удобства
    using B = BigUnsigned;
    using C = typename Difference, BigUnsigned>::Result;
    using Result_T = typename std::conditional< // есть перенос или нет?
        a_n >= b_n, C, typename Difference::Result
    >::type;
    using Result = typename std::conditional< // убираем возможные ведущие нули
        a_n == b_n && std::is_same::value,
        Zero,
        typename Concatenate<
            BigUnsigned,
            Result_T
        >::Result
    >::type;
};

Bit shift implementation

Define the main classes and set the recursion base:

template struct ShiftLeft;
template struct ShiftRight;
template struct BigShiftLeft;
template struct BigShiftRight;
template struct SmallShiftLeft;
template struct SmallShiftRight;
template struct BigShiftLeft    { using Result = Zero; };
template struct BigShiftRight   { using Result = Zero; };
template struct SmallShiftLeft  { using Result = Zero; };
template struct SmallShiftRight { using Result = Zero;
    static const uint32_t carry = 0;
};
template struct BigShiftLeft   , 0> { using Result = BigUnsigned; };
template struct BigShiftRight  , 0> { using Result = BigUnsigned; };
template struct SmallShiftLeft , 0> { using Result = BigUnsigned; };
template struct SmallShiftRight, 0> { using Result = BigUnsigned;
    static const uint32_t carry = 0;
};

I decided that it would be logical to divide any bit shift into the successive application of small (shift less than 32 bits) and large (shift multiple of 32 bits), since their implementations are significantly different. So the big shift:

template
struct BigShiftLeft, shift> {
    using Result = typename Concatenate<
        BigUnsigned<0>,
        typename BigShiftLeft<
            BigUnsigned,
            shift - 1
        >::Result
    >::Result;
};
template
struct BigShiftRight, shift> {
    using Result = typename BigShiftRight<
        BigUnsigned,
        shift - 1
    >::Result;
};

Здесь shift обозначает сдвиг на 32 ⋅ shift бит, и сама операция просто «съедает» или добавляет поочерёдно целые 32-битные слова.

Малый сдвиг — это уже чуть более тонкая работа:

template
struct SmallShiftLeft, shift> {
    static_assert(shift < 32, "shift in SmallShiftLeft must be less than 32 bits");
    static const uint32_t carry = a_0 >> (32 - shift);
    using Result = typename Concatenate<
        BigUnsigned<(a_0 << shift)>,
        typename Sum< // Хватило бы Or или Xor, но Sum у нас уже есть
            typename SmallShiftLeft, shift>::Result,
            BigUnsigned
        >::Result
    >::Result;
};
template
struct SmallShiftRight, shift> {
    static_assert(shift < 32, "shift in SmallShiftRight must be less than 32 bits");
    static const uint32_t carry = a_0 << (32 - shift);
    using Result = typename Concatenate<
        BigUnsigned<(a_0 >> shift) | SmallShiftRight, shift>::carry>,
        typename SmallShiftRight, shift>::Result
    >::Result;
};

Здесь снова приходится заботиться об аккуратном переносе бит.

Наконец, просто сдвиг:

template
struct ShiftLeft {
    using Result = typename BigShiftLeft<
        typename SmallShiftLeft::Result,
        shift / 32
    >::Result;
};
template
struct ShiftRight {
    using Result = typename SmallShiftRight<
        typename BigShiftRight::Result,
        shift % 32
    >::Result;
};

Как и обещано, он просто грамотно использует большой и маленький сдвиги.

Реализация операций сравнения

template struct GreaterThan;
template struct GreaterThanOrEqualTo;
template struct GreaterThan             { static const bool value = false; };
template struct GreaterThanOrEqualTo    { static const bool value = false; };
template<       > struct GreaterThanOrEqualTo { static const bool value = true;  };
template
struct GreaterThanOrEqualTo, Zero> {
    static const bool value = true;
};
template
struct GreaterThan, Zero> {
    static const bool value = n > 0 || GreaterThan, Zero>::value;
};
template
struct GreaterThan, BigUnsigned> {
    using A_tail = BigUnsigned;
    using B_tail = BigUnsigned;
    static const bool value =
        GreaterThan::value || (GreaterThanOrEqualTo::value && a_n > b_n);
};
template
struct GreaterThanOrEqualTo, BigUnsigned> {
    using A_tail = BigUnsigned;
    using B_tail = BigUnsigned;
    static const bool value =
        GreaterThan::value || (GreaterThanOrEqualTo::value && a_n >= b_n);
};
template
struct LessThan {
    static const bool value = !GreaterThanOrEqualTo::value;
};
template
struct LessThanOrEqualTo {
    static const bool value = !GreaterThan::value;
};

Итак, деление. Начнём как положено: с определения классов и задания базы рекурсии.

template
struct Division;
template
struct Division {
    using Quotient = DivisionByZeroError;
    using Residue  = DivisionByZeroError;
};
template
struct Division, One> {
    using Quotient = BigUnsigned;
    using Residue  = Zero;
};
template
struct DummyDivision {
    using Quotient = Zero;
    using Residue  = A;
};

Здесь мы ввели дополнительный класс-пустышку struct DivisionByZeroError {},
единственная функция которого — чуть-чуть скрашивать неказистую жизнь программиста,
пытающегося отладить шаблонную программу. Так, при попытке скомпилировать программу вида

int main(...) {
    ...
    std::cout << BinaryRepresentation::Quotient>::str() << std::endl;
    ...
}

clang выдаст нам предупреждение вроде

static_bignum.cpp:229:18: error: implicit instantiation of undefined template 'BinaryRepresentation'

Зачем нужен загадочный класс DummyDivision, мы сейчас увидим.

Итак, сам алгоритм деления мы будем использовать самый простой (и, вероятно, довольно неэффективный). Пусть надо поделить A на B. Если A меньше B, то решение очевидно: остаток равен A, частное равно 0. (Собственно, очевидное деление и производит вспомогательный класс DummyDivision.) В противном случае пусть Q — это результат деления A на 2B, а R — остаток от этого деления, то есть A = 2BQ + R. Тогда, очевидно, A / B = 2Q + R / B; однако, поскольку R гарантированно меньше 2B, то R / B равно либо 0, либо 1. В свою очередь, A % B = R % B, а R % B равно либо R, либо R - B. Собственно, код:

template
struct Division, BigUnsigned> {
private:
    using A = BigUnsigned; // короткие имена для удобства и т.д. и т.п.
    using B = BigUnsigned;
    using D = typename std::conditional<   // шаг рекурсии: делим на 2B
        GreaterThanOrEqualTo::value,
        Division::Result>,
        DummyDivision                // (или не делим)
    >::type;
    using Q = typename D::Quotient;  // достаём результаты
    using R = typename D::Residue;
public:
    using Quotient = typename Sum<   // складываем 2Q (что, как известно, равно Q << 1) и R / B
        typename SmallShiftLeft::Result,
        typename std::conditional::value, One, Zero>::type
        // спасибо  за std::conditional, который
        // есть не что иное, как тернарный оператор над типами
    >::Result;
    using Residue = typename std::conditional<
        GreaterThanOrEqualTo::value,
        typename Difference::Result,
        R
    >::type;
};

IIIii finally decimal notation! It is clear that to print the decimal representation of a number, you can divide it by 10 for a long time. The remainder of the first division will give the least sign, the remainder of the division of the first quotient by 10 will give the second sign, and so on. However, keep in mind that in C ++ we are not required to print the number digit by digit; we are quite happy to divide the number with the remainder, for example, by 100 to get two signs at once. Therefore, we will divide by the largest number that fits in uint32_t, namely by 10 ⁹ .

template struct DecimalRepresentation;
template<>
struct DecimalRepresentation {
    static inline std::string str(void) {
        return "0";
    }
};
template struct Digit; // тип, достающий младшее слово из длинного числа
template<> struct Digit {
    static const uint32_t value = 0;
};
template
struct Digit> {
    static const uint32_t value = digit;
};
template
struct DecimalRepresentation> {
private:
    static const uint32_t modulo = 1000000000UL;
    static const uint32_t modulo_log = 9;
    using D = Division, BigUnsigned>;
    using Q = typename D::Quotient;
    using R = typename D::Residue;
    static_assert(Digit::value < modulo, "invalid division by power of 10");
public:
    static std::string str(void) {
        // гуру C++ наверняка смогут улучшить этот код, ну а до тех пор пусть лежит такой.
        // просто печатаем десятичные числа в строку, добивая их нулями.
        std::string stail = DecimalRepresentation::str(); // здесь случилась рекурсия
        if(stail == "0") stail = "";
        std::string curr = std::to_string(Digit::value);  // здесь печатаем текущий остаток
        if(stail != "")
            while(curr.size() < modulo_log)
                curr = "0" + curr;
        return stail + curr;
    }
};

And finally, our code

using A = BigUnsigned<0xFFFFFFFFULL>;
using B = One;
using C = Sum::Result;
int main(int argc, char** argv) {
    std::cout << DecimalRepresentation::str() << std::endl;
}

produces 4294967296exactly 2 ³² !

All code together

#include 
#include 
#include 
#include 
#include 
template
struct BigUnsigned {
    static const size_t length = sizeof...(digits);
};
using Zero = BigUnsigned< >;
using One  = BigUnsigned<1>;
template
struct Concatenate {
    using Result = void;
};
template
struct Concatenate, BigUnsigned> { // >> - не проблема для C++11
    using Result = BigUnsigned;
};
template struct Sum;
template struct Sum { using Result = A;    };
template struct Sum<   A, Zero> { using Result = A;    };
// если не определить этот частный случай отдельно, компилятор будет колебаться между предыдущими двумя:
template<       > struct Sum { using Result = Zero; };
template
struct Sum, BigUnsigned> {
    static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0;
    using Result = typename Concatenate<
        BigUnsigned,
        typename Sum<
            typename Sum<
                BigUnsigned, BigUnsigned
            >::Result,
            BigUnsigned
        >::Result
    >::Result;
};
template struct BinaryRepresentation;
template
struct BinaryRepresentation> {
    static std::string str(void) {
        std::bitset<32> bset(a_0);
        return BinaryRepresentation>::str() + bset.to_string();
    }
};
template<>
struct BinaryRepresentation {
    static std::string str(void) {
        return "0b"; // Oppa Python Style
    }
};
template struct Difference;
struct OverflowError {};
template<> struct Difference { using Result = Zero; };
template
struct Difference, Zero> { using Result = BigUnsigned; };
template
struct Difference> { using Result = OverflowError; };
template struct Difference { using Result = OverflowError; };
template struct Difference { using Result = OverflowError; };
template
struct Difference, BigUnsigned > {
    using A = BigUnsigned; // вводим короткие имена для удобства
    using B = BigUnsigned;
    using C = typename Difference, BigUnsigned>::Result;
    using Result_T = typename std::conditional< // есть перенос или нет?
        a_n >= b_n, C, typename Difference::Result
    >::type;
    using Result = typename std::conditional< // убираем возможные ведущие нули
        a_n == b_n && std::is_same::value,
        Zero,
        typename Concatenate<
            BigUnsigned,
            Result_T
        >::Result
    >::type;
};
template struct ShiftLeft;
template struct ShiftRight;
template struct BigShiftLeft;
template struct BigShiftRight;
template struct SmallShiftLeft;
template struct SmallShiftRight;
template struct BigShiftLeft    { using Result = Zero; };
template struct BigShiftRight   { using Result = Zero; };
template struct SmallShiftLeft  { using Result = Zero; };
template struct SmallShiftRight { using Result = Zero;
    static const uint32_t carry = 0;
};
template struct BigShiftLeft   , 0> { using Result = BigUnsigned; };
template struct BigShiftRight  , 0> { using Result = BigUnsigned; };
template struct SmallShiftLeft , 0> { using Result = BigUnsigned; };
template struct SmallShiftRight, 0> { using Result = BigUnsigned;
    static const uint32_t carry = 0;
};
template
struct BigShiftLeft, shift> {
    using Result = typename Concatenate<
        BigUnsigned<0>,
        typename BigShiftLeft<
            BigUnsigned,
            shift - 1
        >::Result
    >::Result;
};
template
struct BigShiftRight, shift> {
    using Result = typename BigShiftRight<
        BigUnsigned,
        shift - 1
    >::Result;
};
template
struct SmallShiftLeft, shift> {
    static_assert(shift < 32, "shift in SmallShiftLeft must be less than 32 bits");
    static const uint32_t carry = a_0 >> (32 - shift);
    using Tail = typename Sum< // здесь хватило бы Or или Xor, но Sum у нас уже есть
        typename SmallShiftLeft, shift>::Result,
        BigUnsigned
    >::Result;
    using Result = typename std::conditional<
        std::is_same>::value, // убираем ведущие нули, если появляются (нормализация!)
        BigUnsigned<(a_0 << shift)>,
        typename Concatenate<
            BigUnsigned<(a_0 << shift)>,
            Tail
        >::Result
    >::type;
};
template
struct SmallShiftRight, shift> {
    static_assert(shift < 32, "shift in SmallShiftRight must be less than 32 bits");
    static const uint32_t carry = a_0 << (32 - shift);
    using Result = typename Concatenate<
        BigUnsigned<(a_0 >> shift) | SmallShiftRight, shift>::carry>,
        typename SmallShiftRight, shift>::Result
    >::Result;
};
template
struct ShiftLeft {
    using Result = typename BigShiftLeft<
        typename SmallShiftLeft::Result,
        shift / 32
    >::Result;
};
template
struct ShiftRight {
    using Result = typename SmallShiftRight<
        typename BigShiftRight::Result,
        shift % 32
    >::Result;
};
template struct GreaterThan;
template struct GreaterThanOrEqualTo;
template struct GreaterThan             { static const bool value = false; };
template struct GreaterThanOrEqualTo    { static const bool value = false; };
template<       > struct GreaterThanOrEqualTo { static const bool value = true;  };
template
struct GreaterThanOrEqualTo, Zero> {
    static const bool value = true;
};
template
struct GreaterThan, Zero> {
    static const bool value = n > 0 || GreaterThan, Zero>::value;
};
template
struct GreaterThan, BigUnsigned> {
    using A_tail = BigUnsigned;
    using B_tail = BigUnsigned;
    static const bool value =
        GreaterThan::value || (GreaterThanOrEqualTo::value && a_n > b_n);
};
template
struct GreaterThanOrEqualTo, BigUnsigned> {
    using A_tail = BigUnsigned;
    using B_tail = BigUnsigned;
    static const bool value =
        GreaterThan::value || (GreaterThanOrEqualTo::value && a_n >= b_n);
};
template
struct LessThan {
    static const bool value = !GreaterThanOrEqualTo::value;
};
template
struct LessThanOrEqualTo {
    static const bool value = !GreaterThan::value;
};
struct DivisionByZeroError { };
template
struct Division;
template
struct Division {
    using Quotient = DivisionByZeroError;
    using Residue  = DivisionByZeroError;
};
template
struct Division, One> {
    using Quotient = BigUnsigned;
    using Residue  = Zero;
};
template
struct DummyDivision {
    using Quotient = Zero;
    using Residue  = A;
};
template
struct Division, BigUnsigned> {
private:
    using A = BigUnsigned;
    using B = BigUnsigned;
    using D = typename std::conditional<
        GreaterThanOrEqualTo::value,
        Division::Result>,
        DummyDivision
    >::type;
    using Q = typename D::Quotient;
    using R = typename D::Residue;
public:
    using Quotient = typename Sum<
        typename SmallShiftLeft::Result,
        typename std::conditional::value, One, Zero>::type
    >::Result;
    using Residue = typename std::conditional<
        GreaterThanOrEqualTo::value,
        typename Difference::Result,
        R
    >::type;
};
template struct DecimalRepresentation;
template<>
struct DecimalRepresentation {
    static inline std::string str(void) {
        return "0";
    }
};
template struct Digit;
template<> struct Digit {
    static const uint32_t value = 0;
};
template
struct Digit> {
    static const uint32_t value = digit;
};
template
struct DecimalRepresentation> {
private:
    static const uint32_t modulo = 1000000000UL;
    static const uint32_t modulo_log = 9;
    using D = Division, BigUnsigned>;
    using Q = typename D::Quotient;
    using R = typename D::Residue;
    static_assert(Digit::value < modulo, "invalid division by power of 10");
public:
    static std::string str(void ){
        std::string stail = DecimalRepresentation::str();
        if(stail == "0") stail = "";
        std::string curr = std::to_string(Digit::value);
        if(stail != "")
            while(curr.size() < modulo_log)
                curr = "0" + curr;
        return stail + curr;
    }
};
using A = BigUnsigned<0xFFFFFFFFULL>;
using B = One;
using C = Sum::Result;
int main(int argc, char** argv) {
    std::cout << DecimalRepresentation::str() << std::endl;
}

What else needs to be said

Firstly, it cannot be said that this is where our long arithmetic is ready. We could
add a lot here: multiplication (in a column), exponentiation, even the
Euclidean algorithm . It’s easy to figure out how to define a class of long numbers with a sign and all the basic operations on it. Secondly, bugs. All code is for training purposes and probably needs debugging. (I debugged the version that appeared before templates with a variable argument, and, unfortunately, only on one compiler.) Let's hope that at least the training goals have been achieved. Third, we must admit that long arithmetic is far from an ideal example.BigSigned

to demonstrate the power of variable argument templates. If you saw interesting and practical examples of using this feature - please share the links in the comments.

Tags:

C ++ 11 variadic templates and long arithmetic at compile time

Parameter packs

Long arithmetic

What else needs to be said

Also popular now: