Jacob Bernoulli's Legacy in Wolfram Language (Mathematica)
- Transfer

Translation of the post by Oleksandr Pavlyk, “ Jacob Bernoulli's Legacy in Mathematica ”.
You can download the translation in the form of a Mathematica document, which contains all the code used in the article, as well as additional materials, here .
January 16, 2015 marks the 360th anniversary of the birth of Jacob Bernoulli .
In [1]: =

Out [2] =

In [3]: =
Out [3] =
In [4]: =
Out [4] =
Jacob Bernoulli became the first mathematician of the famous Bernoulli family , to which many famous mathematicians XVII and XVIII centuries.
The mathematical legacy of Jacob Bernoulli is very rich. He introduced the so-called Bernoulli numbers (Wiki / MathWorld ), found a solution to the Bernoulli differential equation ( Wiki / MathWorld ), studied the Bernoulli process ( Wiki / MathWorld ), proved the Bernoulli inequality ( Wiki / MathWorld ), calculated the number e ( Wiki / MathWorld ), and also revealed the weak law of large numbers (Bernoulli's theorem) ( Wiki / MathWorld ).
In [5]: =
Out [5] =

Bernoulli's Treatise Ars Conjectandi (The Art of Conjecturing ) was posthumously published in 1713, 8 years after his death, and was written in Latin, the lingua franca of his time. It is considered as a fundamental work on probability theory. Its importance is evidenced, in particular, by the fact that it was translated into French by G. Le Roy in 1801 and, recently, into English by ED Sylla in 2005.
Ars Conjectandi consists of 4 parts. The first part reproduces the work of Christian Huygens De Ratiociniis in Ludo Aleae . ( On Reasoning in Games of Chance- About calculations in a game of chance) with extensive comments from Bernoulli and detailed solutions to the five Huygens problems posed at the end of Huygens's work with answers, but without proof. In the first part, Bernoulli also deduces the probability that among n independent trials there will be at least m successful if the probability of success in each test is p :

The second part of “The Doctrine of Permutations and Combinations” is devoted to combinatorics and the study of curly numbers ( Wiki / MathWorld ), i.e. numbers that can be represented as a set of points located on a plane in the form of regular geometric shapes:
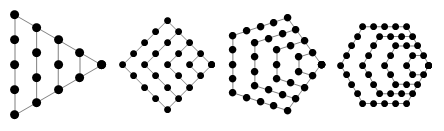
It was in this part that Bernoulli introduced the so-called Bernoulli numbers. He began by saying that the revealed relation for the binomial coefficients
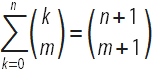 .
. In [6]: =

Out [6] =
Bernoulli knew that for a fixed value of the number m , the binomial coefficient
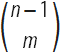 is a polynomial in the variable n , namely
is a polynomial in the variable n , namely 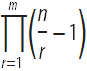 . This identity allowed him to derive the values of the sums of the degrees of natural numbers
. This identity allowed him to derive the values of the sums of the degrees of natural numbers In order to reproduce the table obtained by Bernoulli, we create a function defining equations for the sums of the degrees of natural numbers:
In [7]: =

In [8]: =
Out [8] =
In [9]: =
Out [9] =
In [10]: =
Out [10] =
Solving the resulting system of equations, we get:
In [11]: =

Out [11] =
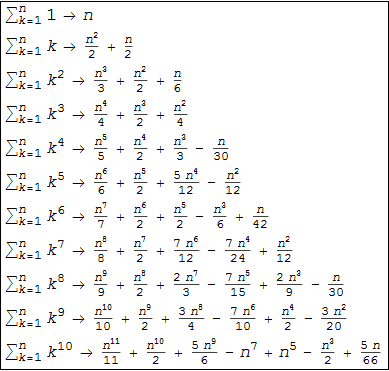
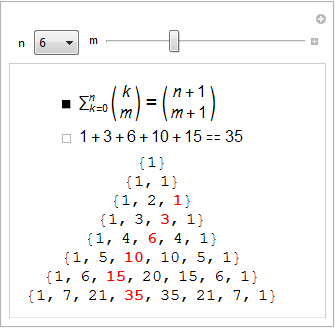
Bernoulli wrote that “Anyone who has carefully studied the obtained sequence can continue the Table further without any additional calculations ”, noting that:

He noted that the coefficients
In [12]: =
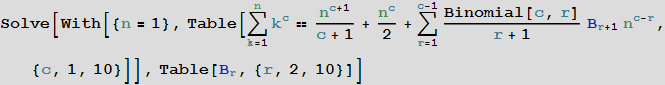
Out [12] =
These coefficients are the well-known Bernoulli numbers that have found their application in many areas of mathematics [for example, see the discussion Why do Bernoulli numbers arise everywhere?(Why are Bernoulli numbers appearing everywhere?) On mathoverflow.net]:
In [13]: =
Out [13] =
In the second part of his book, Bernoulli calculates the number of possible permutations, the number of permutations in a set with repeating elements, the number of ways to select given objects from the set, etc., which he later uses to calculate probability, as the ratio of the number of favorable events to the total possible number of events.
In the third part, Bernoulli applies the results obtained in the previous two parts to the solution of 24 problems related to gambling. The leitmotif of all these tasks is the sequence of independent results 0 and 1, which is called the “Bernoulli process”. I think that the 360th anniversary of the birth of Jacob Bernoulli is an excellent occasion to solve his problems in Mathematica using the Wolfram Language.
For example, in task 9, it is required to find the expected win in a game of three players. Players alternately take cards (without replacement and return) from the deck of 20 cards, while 10 of them are curly. When the cards run out, the winnings are distributed evenly among those players who have more curly cards.
Put c1 , c2, and c3 is the number of figure cards for each player, then the winning share of the first player will be:
In [14]: =

Assume that after a deck of 20 cards was thus distributed between the players, it turns out that the first and second they have 7 cards each, and the third one has 6. The final distribution vector of curly cards between players has a multidimensional hypergeometric distribution, which is set in the Wolfram Language function MultivariateHypergeometricDistribution :
In [15]: =
In [16]: =
Out [16] =
In [ 17]: =
Out [17] =
This and other tasks are considered and solved in the attached document (in English).
In the final part of the treatiseArs Conjectandi discusses the use of probability theory in solving civil, moral and economic issues. In this part, Bernoulli argues that probability theory reflects our incomplete knowledge of the state of the world, and, unlike gambling, where probability can be determined by finding the ratio of the number of favorable outcomes of some experience to their total possible number, probability in “real” life is not can be installed a priori. Bernoulli argues that these unknown probabilities can be calculated based on past results.
He proved the weak law of large numbers, which states that the observed success rate in a series of n independent trials, the probability of success in each of which is equal to p, will infinitely approach p with an unlimited increase in the number of trials. Thus, we can estimate the probability with arbitrary accuracy by taking a sufficient number of tests. Thus, for any δ and e , there exists a number n (number of tests) that
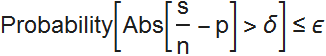
In [18]: =

Out [18] =
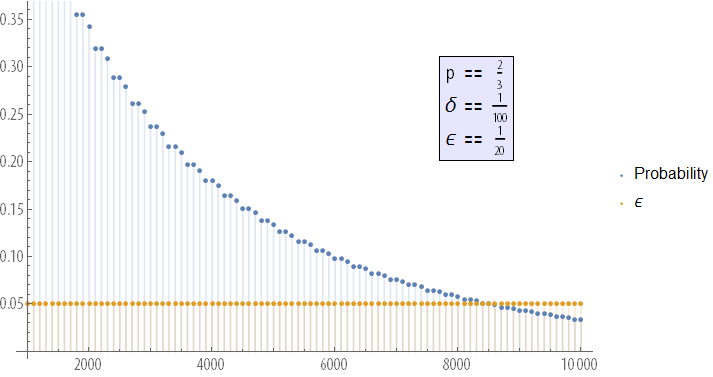
Demonstration of " Imitation of a coin flip, and the law of large numbers of experiment " ( Simulated Coin Tossing Experiments and the Law of Large Numbers ), created by Ian McLeod for the Wolfram Demonstrations Project, in particular, demonstrates this convergence process.
Resources for learning Wolfram Language (Mathematica) in Russian: habrahabr.ru/post/244451
