Padding Oracle Attack or why cryptography scares
- Transfer
We all know that cryptographic primitives should not be independently implemented. We are also aware that even if we trickyly expand the order of letters in all words of the message, shift each letter in the alphabetical order by 5 positions and dilute the text with random phrases in order to lead attackers out of the way, our wonderful code will most likely reveal any friend a person with cryptography (and in this case, a reasonably smart 12-year-old teenager will cope with the task).
However, the introduction of well-known and robust algorithms is not a panacea. Even if you take a ready-made implementation of this algorithm, generate secret keys according to all the requirements and the like, anyway you will remain potentially exposed to some very effective attacks. An experienced attacker is tiny enough, it would seem, completely unrelated to the cryptosystem a bit of information to circumvent encryption.
My message is not to convince you to abandon the independent use of cryptographic tools or to go and hire a consultant with a salary of $ 1000 per hour every time you think about encryption.
In part, I mean that you should never relax, you should always be on the lookout for ways that an attacker can use to get more information about your system, and in part that Padding Oracle Attack is a cool demonstration of all this. So, let's begin.
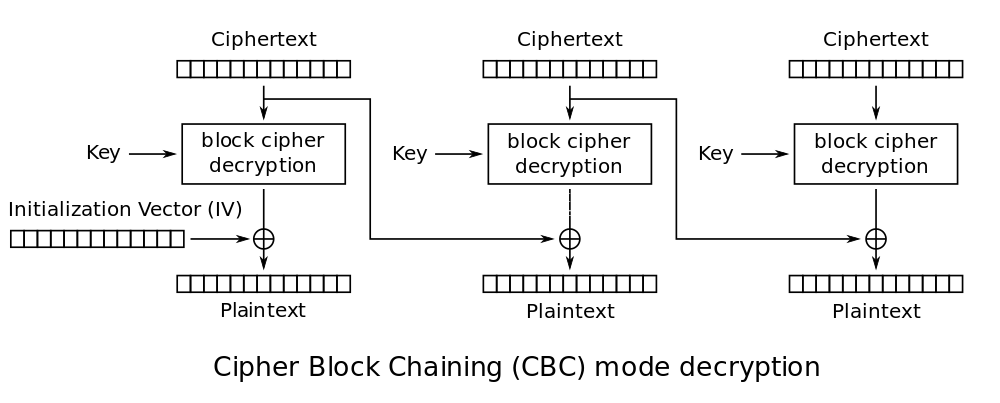
CBC, or ciphertext block interlocking mode, is one of the symmetric block encryption modes using the feedback mechanism. This means that during encryption, the next block of plaintext passes through the block encryption algorithm, and is also additionally modified using the encryption result of the previous block.
So if we encrypt the sentence:
we get the encryption result for each block of 16 bytes, and the last block of plaintext will be supplemented in a special way (but more on that later).
In CBC, each block of plaintext is added bitwise modulo two (xor) with the previous ciphertext block before entering the encryption algorithm. This block interdependence means that each ciphertext block depends on each plaintext block that has been processed to date. Moreover, changing any byte of plaintext will lead to a change in all subsequent bytes of the ciphertext (avalanche effect, yeah). According to Wikipedia, CBC is “one of two symmetric block encryption modes recommended by Neil Ferguson and Bruce Schneier.”
The preferred method of padding ciphertext blocks is PKCS7. In it, the value of each padded byte is set equal to the number of padded bytes. So if we have a block of 12 characters, it will be padded with four bytes [04, 04, 04, 04] to a standard block size of 16 bytes. If the block is 15 bytes in size, it will be padded with one byte [01]. If the block is exactly 16 bytes in size, we add a new block consisting of [16] * 16 . (more details - https://en.wikipedia.org/wiki/Padding_(cryptography)#PKCS7 )
According to this method, the last block of decrypted plaintext cannot end, for example, on [..., 13, 06, 05]. This means that the original ciphertext is also incorrect, because there are no valid plaintexts that could be converted into such ciphertext.
It turns out that the knowledge of the fact is that when decrypting the ciphertext the plaintext is obtained with the correct addition that is sufficient for the attacker to conduct a successful attack on encryption in CBC mode. If we can provide cryptographic texts to some service, and it will return information to us whether the addition is correct, we can open ANY ciphertext.
So an error that is enough to bring down your encryption may be some API that will return a 200 code if the ciphertext that we submitted is decrypted into something with the correct addition, and a 500 code if not.
This is not an unlikely situation. For example, Ruby OpenSSL is prone to this problem. It is enough to use the sample code from the official documentation (http://www.ruby-doc.org/stdlib-1.9.3/libdoc/openssl/rdoc/OpenSSL/Cipher.html#documentation ):
This code throws OpenSSL :: Cipher :: CipherError: bad decrypt , which, if not intercepted, will return a 500 error response .
Suppose we stole the ciphertext. If we can send ciphertexts and determine whether they are decrypted into messages with the correct addition, how can we use this to completely decrypt the stolen ciphertext?
Once again, in CBC mode, each block of plaintext is added bitwise modulo two (XOR) with the previous ciphertext block before entering the cipher. When decrypting, each ciphertext passes through a decryptor and then XOR’s with the previous ciphertext block to produce plaintext.
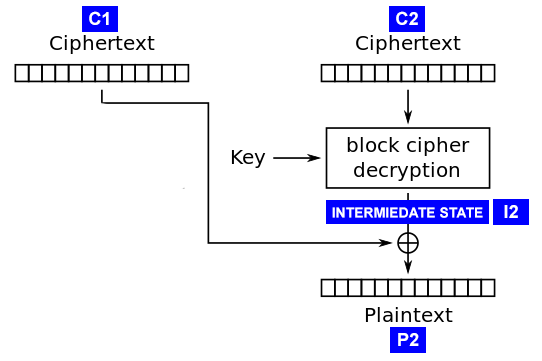
The attack works by calculating the “intermediate state” of the decryption procedure (see diagram) for each ciphertext block. This is the state of the ciphertext block after decryption by the block algorithm, but BEFORE the XOR procedure with the previous ciphertext block. We will find this state, rising from the bottom of the clear text, instead of going down through the block cipher. Also, we will not worry at all about the encryption key or the block encryption algorithm.
Why is this intermediate state so important? Note:
We already know C1 because this is part of the ciphertext we have. So if we find I2, we can easily find P2 and decrypt the message.

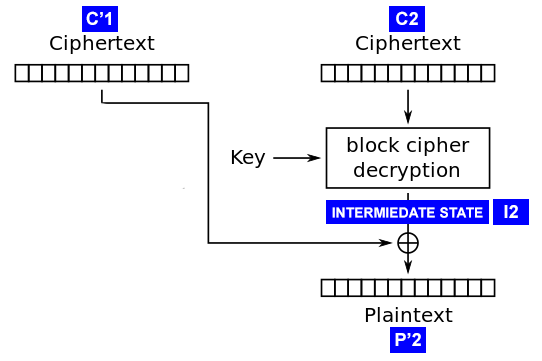
Recall that we can supply any ciphertext to the system input, and the server will tell us whether the correct addition is obtained after decryption. We use this fact by feeding C1 '+ C2 to the input , where C1' is the ciphertext block that we specially formed, and C2 is the block we want to decrypt. By C1 '+ C2 we mean simple concatenation (that is, “gluing” blocks). Denote the result of decryption as P'2 .
To begin with, we fill C1 '[1..15] with random bytes, and fill C1' [16] with zero ( 0x00 ). Now we give C1 '+ C2to the server. If the server answers that the add-on is correct, then we can be sure (with a high probability) that P2 '[16] is 0x01 (because the add-on is correct). If the server responds with an error, send a message with C1 '[16] set to 0x01 , then to 0x02 , etc. until we get the answer we need.
Now suppose that the server returned a response of 200 with C1 '[16] = 94 .
Hurrah! We got the final byte of the intermediate state. Because C2 is taken from the real ciphertext, then I2 is also identical to the real one. Therefore, we can decrypt the last byte of the real plaintext:
We feed C1 '[16] = C1 [16] and get the last byte of real plaintext. At this point, we only found a placeholder, so we’ll have to do a few more iterations of the process until we find something interesting.
We found the last byte by scrolling C1 ' until we got the correct complement. In this case, we can conclude that the last byte of P'2 is 0x01 . Then using P2 '[16] and C1' [16] , we find I2 [16] . Continuing this process, we find the remaining bytes of I2 and decrypt the entire ciphertext block.
Fill C1 '[1..14] random bytes, C1' [15] set to 0x00 , and C1 '[16] such as to obtain P2' [16] == 0x02 :
Now we can be sure that P2 ' will end with 0x02, and therefore the only option where P2' will have the correct complement is if P2 [16] == 0x02 . We will scroll C1 '[15] until the server gives us the code 200 . Suppose this happened at C1 '[15] == 106 . We do again what we already know:
And voila! We know the penultimate byte of I2 . Therefore, we can find the penultimate byte of P2 , as we already did before:
And so on for all 16 bytes of C2 .
The shape of the ciphertext blocks depends only on them and the previous blocks. So we can apply the above algorithm to each block of ciphertext (separately from the first). The first block will be encrypted using the initialization vector ( IV ), and the IV itself is randomly selected during the encryption procedure. Until we recognize IV , we will not be able to decrypt the first block, and there is nothing that can be thought up here, except for a stupid enumeration of the obvious values [0,0,0, ...] for IV and see if any Any reasonable clear text. And do so in the hope that the first 16 bytes will be something like " Dear Eugene! ".
That's all there isPadding Oracle Attack .
That's why everything related to cryptography is scary.
We know that cryptographic primitives should not be independently implemented, and that we are building the system on something already invented. It is easy to feel relaxed when we hide behind a strong cipher developed by specialists. And while we keep our keys secret and do not keep open texts anywhere, we feel invulnerable.
But, as you just saw, the smallest third-party channel, a drop of information, is enough to make the system completely vulnerable. Our imaginary developer used a persistent algorithm from an existing library, generated keys of the required length and did not do anything stupid, like reusing temporary values ( nonce) His only mistake was not to catch the non-obvious exception, which led us to the opportunity to understand whether our ciphertext is decrypted into something correct.
Of course, specifically this attack can be prevented by catching exceptions, limiting the number of requests from one IP address and monitoring suspicious requests, but this is not the point. Attackers are always sophisticated and will use even the slightest imperfection of implementation. Be careful with your cryptography, even if it is taken from a reliable source.
Thanks.
The Matasano Crypto Challenges ( http://matasano.com/articles/crypto-challenges/ ), which made me interested in cryptography. Highly recommend!
_____
Translation made with permission of the author of the article Robert Heaton.
Source: http://robertheaton.com/2013/07/29/padding-oracle-attack/
More interesting related links:
https://class.coursera.org/crypto-preview/lecture/38

However, the introduction of well-known and robust algorithms is not a panacea. Even if you take a ready-made implementation of this algorithm, generate secret keys according to all the requirements and the like, anyway you will remain potentially exposed to some very effective attacks. An experienced attacker is tiny enough, it would seem, completely unrelated to the cryptosystem a bit of information to circumvent encryption.
My message is not to convince you to abandon the independent use of cryptographic tools or to go and hire a consultant with a salary of $ 1000 per hour every time you think about encryption.
In part, I mean that you should never relax, you should always be on the lookout for ways that an attacker can use to get more information about your system, and in part that Padding Oracle Attack is a cool demonstration of all this. So, let's begin.
CBC mode
CBC, or ciphertext block interlocking mode, is one of the symmetric block encryption modes using the feedback mechanism. This means that during encryption, the next block of plaintext passes through the block encryption algorithm, and is also additionally modified using the encryption result of the previous block.
So if we encrypt the sentence:
This is a sentence of a carefully chosen length.
we get the encryption result for each block of 16 bytes, and the last block of plaintext will be supplemented in a special way (but more on that later).
In CBC, each block of plaintext is added bitwise modulo two (xor) with the previous ciphertext block before entering the encryption algorithm. This block interdependence means that each ciphertext block depends on each plaintext block that has been processed to date. Moreover, changing any byte of plaintext will lead to a change in all subsequent bytes of the ciphertext (avalanche effect, yeah). According to Wikipedia, CBC is “one of two symmetric block encryption modes recommended by Neil Ferguson and Bruce Schneier.”

How block additions work (important!)
The preferred method of padding ciphertext blocks is PKCS7. In it, the value of each padded byte is set equal to the number of padded bytes. So if we have a block of 12 characters, it will be padded with four bytes [04, 04, 04, 04] to a standard block size of 16 bytes. If the block is 15 bytes in size, it will be padded with one byte [01]. If the block is exactly 16 bytes in size, we add a new block consisting of [16] * 16 . (more details - https://en.wikipedia.org/wiki/Padding_(cryptography)#PKCS7 )
According to this method, the last block of decrypted plaintext cannot end, for example, on [..., 13, 06, 05]. This means that the original ciphertext is also incorrect, because there are no valid plaintexts that could be converted into such ciphertext.
The Padding Oracle Attack
It turns out that the knowledge of the fact is that when decrypting the ciphertext the plaintext is obtained with the correct addition that is sufficient for the attacker to conduct a successful attack on encryption in CBC mode. If we can provide cryptographic texts to some service, and it will return information to us whether the addition is correct, we can open ANY ciphertext.
So an error that is enough to bring down your encryption may be some API that will return a 200 code if the ciphertext that we submitted is decrypted into something with the correct addition, and a 500 code if not.
This is not an unlikely situation. For example, Ruby OpenSSL is prone to this problem. It is enough to use the sample code from the official documentation (http://www.ruby-doc.org/stdlib-1.9.3/libdoc/openssl/rdoc/OpenSSL/Cipher.html#documentation ):
decipher = OpenSSL::Cipher::AES.new(128, :CBC)
decipher.decrypt
decipher.key = "the most secret!"
decipher.iv = "also very secret"
plain = decipher.update("thewrongpadding!") + decipher.final
This code throws OpenSSL :: Cipher :: CipherError: bad decrypt , which, if not intercepted, will return a 500 error response .
Suppose we stole the ciphertext. If we can send ciphertexts and determine whether they are decrypted into messages with the correct addition, how can we use this to completely decrypt the stolen ciphertext?
The intermediate state
Once again, in CBC mode, each block of plaintext is added bitwise modulo two (XOR) with the previous ciphertext block before entering the cipher. When decrypting, each ciphertext passes through a decryptor and then XOR’s with the previous ciphertext block to produce plaintext.

The attack works by calculating the “intermediate state” of the decryption procedure (see diagram) for each ciphertext block. This is the state of the ciphertext block after decryption by the block algorithm, but BEFORE the XOR procedure with the previous ciphertext block. We will find this state, rising from the bottom of the clear text, instead of going down through the block cipher. Also, we will not worry at all about the encryption key or the block encryption algorithm.
Why is this intermediate state so important? Note:
I2 = C1 ^ P2
и
P2 = C1 ^ I2
We already know C1 because this is part of the ciphertext we have. So if we find I2, we can easily find P2 and decrypt the message.

Ciphertext Manipulation
Recall that we can supply any ciphertext to the system input, and the server will tell us whether the correct addition is obtained after decryption. We use this fact by feeding C1 '+ C2 to the input , where C1' is the ciphertext block that we specially formed, and C2 is the block we want to decrypt. By C1 '+ C2 we mean simple concatenation (that is, “gluing” blocks). Denote the result of decryption as P'2 .
To begin with, we fill C1 '[1..15] with random bytes, and fill C1' [16] with zero ( 0x00 ). Now we give C1 '+ C2to the server. If the server answers that the add-on is correct, then we can be sure (with a high probability) that P2 '[16] is 0x01 (because the add-on is correct). If the server responds with an error, send a message with C1 '[16] set to 0x01 , then to 0x02 , etc. until we get the answer we need.
(translator’s note. Of course, a situation is possible when we get two correct answers:
1) for complement 01
2) for supplement 02.02 or 03.03.03 ...
If this situation occurs, just change the penultimate byte C1 'and repeat the operation again .
In the worst case, we will need three attempts, but this is unlikely.
)

Now suppose that the server returned a response of 200 with C1 '[16] = 94 .
I2 = C1' ^ P2'
I2[16] = C1'[16] ^ P2'[16]
= 94 ^ 01
= 95
Hurrah! We got the final byte of the intermediate state. Because C2 is taken from the real ciphertext, then I2 is also identical to the real one. Therefore, we can decrypt the last byte of the real plaintext:
P2[16] = C1[16] ^ I2[16]
= C1[16] ^ 95
We feed C1 '[16] = C1 [16] and get the last byte of real plaintext. At this point, we only found a placeholder, so we’ll have to do a few more iterations of the process until we find something interesting.
Continue
We found the last byte by scrolling C1 ' until we got the correct complement. In this case, we can conclude that the last byte of P'2 is 0x01 . Then using P2 '[16] and C1' [16] , we find I2 [16] . Continuing this process, we find the remaining bytes of I2 and decrypt the entire ciphertext block.
Fill C1 '[1..14] random bytes, C1' [15] set to 0x00 , and C1 '[16] such as to obtain P2' [16] == 0x02 :
C'1[16] = P'2[16] ^ I2[16]
= 02 ^ 95
= 93
Now we can be sure that P2 ' will end with 0x02, and therefore the only option where P2' will have the correct complement is if P2 [16] == 0x02 . We will scroll C1 '[15] until the server gives us the code 200 . Suppose this happened at C1 '[15] == 106 . We do again what we already know:
I2 = C1' ^ P2'
I2[15] = C1'[15] ^ P2'[15]
= 106 ^ 02
= 104
And voila! We know the penultimate byte of I2 . Therefore, we can find the penultimate byte of P2 , as we already did before:
P2[15] = C1[15] ^ I2[15]
= C1[15] ^ 104
And so on for all 16 bytes of C2 .
Other blocks
The shape of the ciphertext blocks depends only on them and the previous blocks. So we can apply the above algorithm to each block of ciphertext (separately from the first). The first block will be encrypted using the initialization vector ( IV ), and the IV itself is randomly selected during the encryption procedure. Until we recognize IV , we will not be able to decrypt the first block, and there is nothing that can be thought up here, except for a stupid enumeration of the obvious values [0,0,0, ...] for IV and see if any Any reasonable clear text. And do so in the hope that the first 16 bytes will be something like " Dear Eugene! ".
That's all there isPadding Oracle Attack .
That's why everything related to cryptography is scary.
We know that cryptographic primitives should not be independently implemented, and that we are building the system on something already invented. It is easy to feel relaxed when we hide behind a strong cipher developed by specialists. And while we keep our keys secret and do not keep open texts anywhere, we feel invulnerable.
But, as you just saw, the smallest third-party channel, a drop of information, is enough to make the system completely vulnerable. Our imaginary developer used a persistent algorithm from an existing library, generated keys of the required length and did not do anything stupid, like reusing temporary values ( nonce) His only mistake was not to catch the non-obvious exception, which led us to the opportunity to understand whether our ciphertext is decrypted into something correct.
Of course, specifically this attack can be prevented by catching exceptions, limiting the number of requests from one IP address and monitoring suspicious requests, but this is not the point. Attackers are always sophisticated and will use even the slightest imperfection of implementation. Be careful with your cryptography, even if it is taken from a reliable source.
Thanks.
The Matasano Crypto Challenges ( http://matasano.com/articles/crypto-challenges/ ), which made me interested in cryptography. Highly recommend!
_____
Translation made with permission of the author of the article Robert Heaton.
Source: http://robertheaton.com/2013/07/29/padding-oracle-attack/
More interesting related links:
https://class.coursera.org/crypto-preview/lecture/38
