We play with genetic algorithms
One Saturday December evening, I was sitting over the book The Blind Watchmaker , and I was struck by an incredibly interesting experiment: take any sentence, for example, Shakespeare’s string: Methinks it is like a weasel and a random string of the same length: wdltmnlt dtjbkwirzrezlmqco p and start making random changes to it. How many generations will this random string turn into a Shakespearean line if only descendants more similar to Shakespearean survive?
Today we will repeat this experiment, but on a completely different scale.

Article structure:
Caution traffic!
In the field of artificial intelligence, a genetic algorithm is understood to mean heuristics for finding solutions based on natural selection. It is usually used for tasks where the search space is so huge that it is impossible to find an exact solution and the heuristic solution satisfies the requirements. The task itself has some function of the quality of the solution, which must be maximized.
In its simplest form, the genetic algorithm has the following structure (see diagram): we start with some solution, in our case, this is a random string; make mutations, for example, change a randomly selected letter in a string to a randomly selected letter and get a new set of strings ( kmutations per line); from them we select only those that are closer to Shakespearean (by the number of matching characters), for example 10 such lines, if Shakespearean is not among them, then we start the process again.
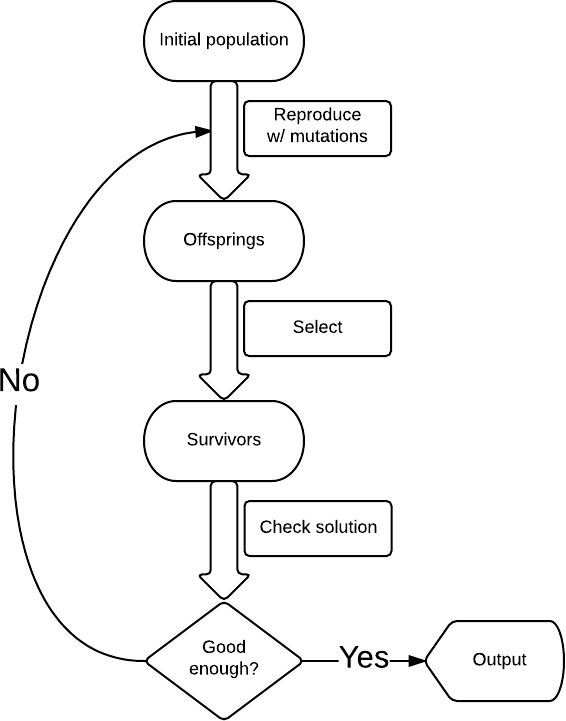
In many respects, genetic algorithms are similar to classical optimization methods, a population is a set of current points, mutations are a study of neighboring points, selection is a selection of new points for finding a solution in the conditions of limited computing resources.
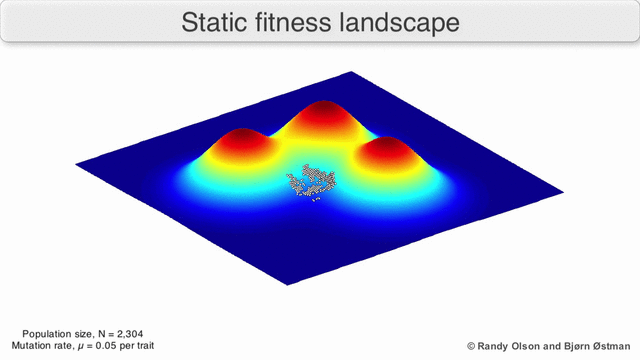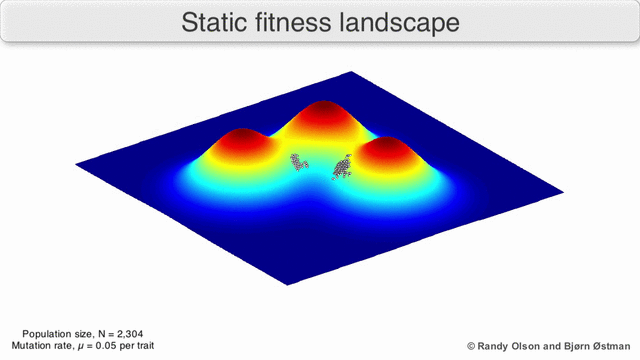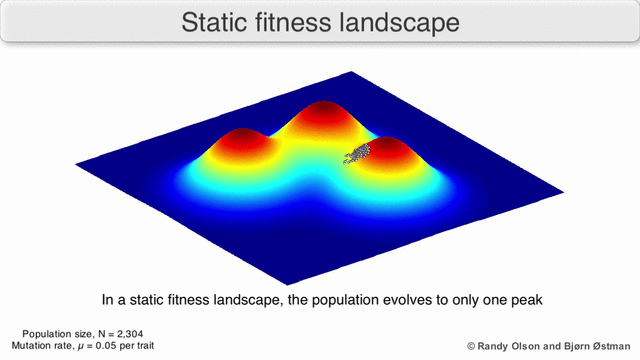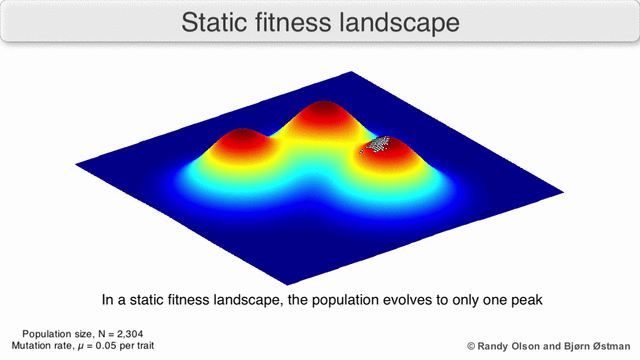
The population always tends to the nearest maximum, since we select the current search points as having the maximum value (all other points “die” will not withstand competition with the nearest maximum). Since the population size is significant, which means that the probability of at least one step in the direction of the maximum is not negligible, then after a certain number of steps the population will shift towards the local maximum. And the descendants of a point shifted closer to the maximum have greater “survival”. So after a sufficient number of steps, the descendants of this point will begin to dominate the population and all of it will shift to the maximum.
Visualization of a population tending to a local maximum:
(due to Randy Olson )
Input : string S
Output : natural number N , equal to the number of generations needed to convert a random string of length len ( S ) to string S
What is a mutation in our case ? By mutating a string S, we mean replacing one randomly selected character from a string S with another arbitrary character in the alphabet. In this task, we use only lowercase Latin characters and a space.
What is the initial population (initial population in the scheme)? This random string of equal length input string S .
What are descendants(offsprings)? Suppose we fix the number of mutations of one line per constant k , then the descendants are k mutations of each line of the current generation.
What are survivors ? Suppose we have fixed the size of the population at a constant h , then the survivors - it h strings most similar to the input string the S .
In pseudocode (suspiciously similar to python), it looks like this:

Consider the following line: The quick brown fox jumps over the lazy dog and reproduce the output of our program for it:
Consider the chain of changes (generation number on the left):
As we see, each generation differs by no more than one symbol from each other. It took a total of 46 generations to get from rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopyk to the quick brown fox jumps over the lazy dog through mutations and selection.
Some examples, the Shakespearean line or the English pangram about the fox, are interesting, but not too convincing. Therefore, I decided to consider a more interesting question: what will happen if we take a couple of classical works, break them down into sentences and calculate the number of generations for each of them? What will be the nature of the dependence of the number of generations on the string (for example, on its length)?
I chose To Kill a Mocking Bird by Harper Lee (Kill a Mockingbird, Harper Lee) and Catcher in the Rye by JD Salinger (The Catcher in the Rye, JD Salinger) as classic works. We will measure two parameters - the distribution of the number of generations by sentences and the dependence of the number of generations on the length of the string (is there a correlation?).
The parameters were as follows: the number of descendants of the line: 100; the number of survivors in a generation: 10.
As we can see, for the majority of sentences it was possible to reach the line quickly enough, less than 100 iterations are required, almost iterations are enough for 200 iterations (among all the sentences there was only one that needed 1135 iterations, judging by the sentence, the breakdown algorithm made a mistake and glued several sentences into one ): The

correlation between string length and number of generations is perfect. This means that almost every generation managed to move one step closer to the target line.
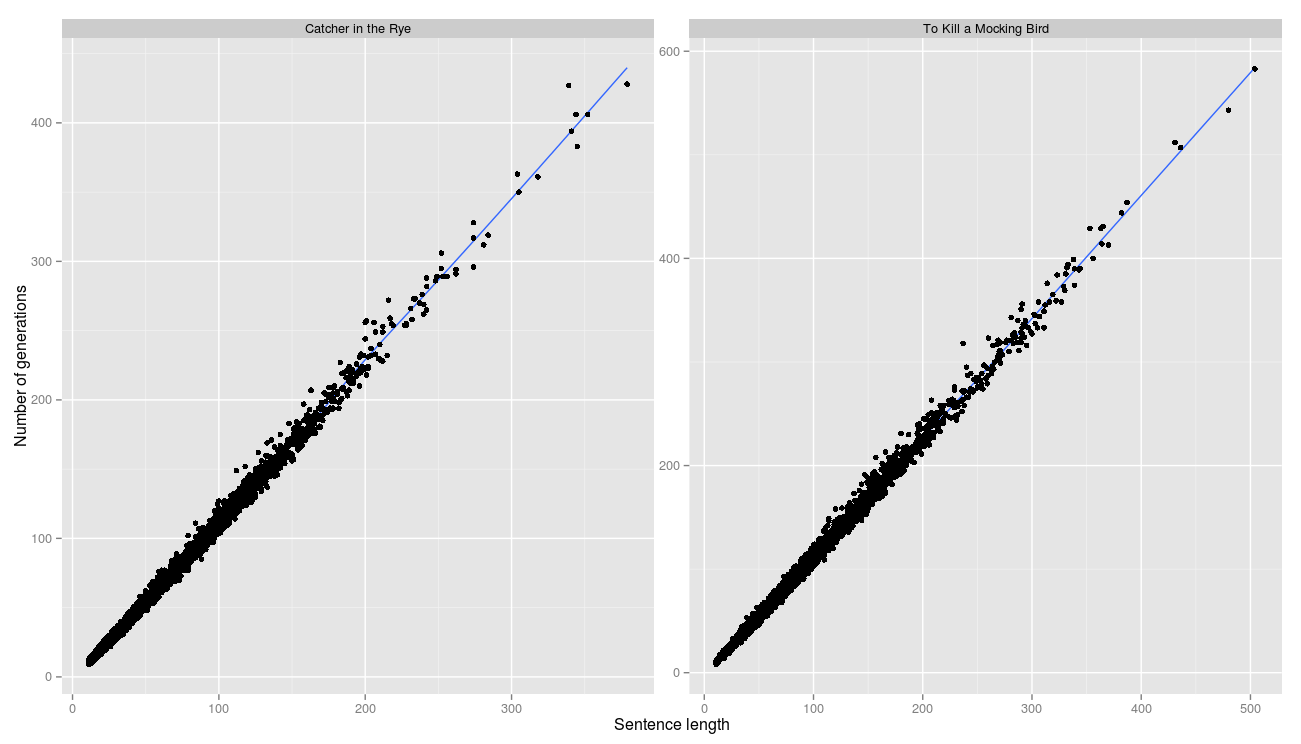
R ^ 2 is 0.996 and 0.997 respectively.
Thus, it was experimentally established that under the conditions of our problem for any input string S , the number of generations linearly depends on the length of the string, which is consistent with the initial assumptions.
All code, python - genetic algorithm \ text processing and R - visualization, available on github:
github.com/SergeyParamonov/genetics-experiments
We figured out the basic structure of genetic algorithms and applied strings to solve the problem of mutation. As a result of experiments with classical texts, we found that in our conditions there is a linear relationship between the length of the string and the number of generations necessary to reach the input string.
We also noted that the basic search structure can be modified (for example, using crossover - using several generation members to create descendants) to solve a wide class of optimization problems where it is too difficult to find the exact solution.
Today we will repeat this experiment, but on a completely different scale.

Article structure:
- What is a genetic algorithm?
- Why does it work
- We formalize the problem with a random string
- Algorithm Operation Example
- Classic experiments
- Code and data
- conclusions
Caution traffic!
What is a genetic algorithm?
In the field of artificial intelligence, a genetic algorithm is understood to mean heuristics for finding solutions based on natural selection. It is usually used for tasks where the search space is so huge that it is impossible to find an exact solution and the heuristic solution satisfies the requirements. The task itself has some function of the quality of the solution, which must be maximized.
In its simplest form, the genetic algorithm has the following structure (see diagram): we start with some solution, in our case, this is a random string; make mutations, for example, change a randomly selected letter in a string to a randomly selected letter and get a new set of strings ( kmutations per line); from them we select only those that are closer to Shakespearean (by the number of matching characters), for example 10 such lines, if Shakespearean is not among them, then we start the process again.

Why does it work
In many respects, genetic algorithms are similar to classical optimization methods, a population is a set of current points, mutations are a study of neighboring points, selection is a selection of new points for finding a solution in the conditions of limited computing resources.
The population always tends to the nearest maximum, since we select the current search points as having the maximum value (all other points “die” will not withstand competition with the nearest maximum). Since the population size is significant, which means that the probability of at least one step in the direction of the maximum is not negligible, then after a certain number of steps the population will shift towards the local maximum. And the descendants of a point shifted closer to the maximum have greater “survival”. So after a sufficient number of steps, the descendants of this point will begin to dominate the population and all of it will shift to the maximum.
Visualization of a population tending to a local maximum:

(due to Randy Olson )
We formalize the problem with a random string
Input : string S
Output : natural number N , equal to the number of generations needed to convert a random string of length len ( S ) to string S
What is a mutation in our case ? By mutating a string S, we mean replacing one randomly selected character from a string S with another arbitrary character in the alphabet. In this task, we use only lowercase Latin characters and a space.
What is the initial population (initial population in the scheme)? This random string of equal length input string S .
What are descendants(offsprings)? Suppose we fix the number of mutations of one line per constant k , then the descendants are k mutations of each line of the current generation.
What are survivors ? Suppose we have fixed the size of the population at a constant h , then the survivors - it h strings most similar to the input string the S .
In pseudocode (suspiciously similar to python), it looks like this:

Algorithm Operation Example
Consider the following line: The quick brown fox jumps over the lazy dog and reproduce the output of our program for it:
Consider the chain of changes (generation number on the left):
1 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopyk 2 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquzmopyk 3 rbb mffwfhwtxnjjiozz ujhhlxeoyhezarquzmopyk 4 rbb mffwfhwtxnjjiozz ujhhlxeoyhezarquzmodyk 5 rbb mffwfhbtxnjjiozz ujhhlxeoyhezarquzmodyk 6 rbb mffcfhbtxnjjiozz ujhhlxeoyhezarquzmodyk 7 rbb mffcf btxnjjiozz ujhhlxeoyhezarquzmodyk 8 rbb mffcf btxnjjiozz ujhhlxeoyheza quzmodyk 9 rbb mffcf brxnjjiozz ujhhlxeoyheza quzmodyk 10 rbb mffcf brxnjjiozz ujphlxeoyheza quzmodyk 20 rbb mffcf bronj fox jujpslxveyheza luzmodyk 30 rbb mficf bronj fox jumps overhehe luzy dyg 40 he m ick bronn fox jumps over the lazy dog 41 he q ick bronn fox jumps over the lazy dog 42 he q ick bronn fox jumps over the lazy dog 43 he q ick brown fox jumps over the lazy dog 44 he quick brown fox jumps over the lazy dog 45 ahe quick brown fox jumps over the lazy dog 46 the quick brown fox jumps over the lazy dog
Full conclusion
print_genes ("The quick brown fox jumps over the lazy dog")
1 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopyk
2 rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquzmopyk
3 rbb mffwfhwtxnjjiozz ujhhlxeoyhezarquzmopyk
4 rbb mffwfhwtxnjjiozz ujhhlxeoyhezarquzmodyk
5 rbb mffwfhbtxnjjiozz ujhhlxeoyhezarquzmodyk
6 rbb mffcfhbtxnjjiozz ujhhlxeoyhezarquzmodyk
7 rbb mffcf btxnjjiozz ujhhlxeoyhezarquzmodyk
8 rbb mffcf btxnjjiozz ujhhlxeoyheza quzmodyk
9 rbb mffcf brxnjjiozz ujhhlxeoyheza quzmodyk
10 rbb mffcf brxnjjiozz ujphlxeoyheza quzmodyk
11 rbb mffcf brxnj iozz ujphlxeoyheza quzmodyk
12 rbb mffcf brxnj ioz ujphlxeoyheza quzmodyk
13 rbb mffcf bronj ioz ujphlxeoyheza quzmodyk
14 rbb mffcf bronj ioz ujphlxeeyheza quzmodyk
15 rbb mffcf bronj ioz ujphlxeeyheza luzmodyk
16 rbb mffcf bronj ioz ujphlxveyheza luzmodyk
17 rbb mffcf bronj foz ujphlxveyheza luzmodyk
18 rbb mffcf bronj foz jujphlxveyheza luzmodyk
19 rbb mffcf bronj foz jujpslxveyheza luzmodyk
20 rbb mffcf bronj fox jujpslxveyheza luzmodyk
21 rbb mffcf bronj fox jujpslxveyheza luzm dyk
22 rbb mffcf bronj fox jujpslxverheza luzm dyk
23 rbb mffcf bronj fox jumpslxverheza luzm dyk
24 rbb mffcf bronj fox jumpslxverheha luzm dyk
25 rbb mffcf bronj fox jumpslxverhehe luzm dyk
26 rbb mffcf bronj fox jumps xverhehe luzm dyk
27 rbb mffcf bronj fox jumps xverhehe luzm dyg
28 rbb mffcf bronj fox jumps xverhehe luzy dyg
29 rbb mffcf bronj fox jumps overhehe luzy dyg
30 rbb mficf bronj fox jumps overhehe luzy dyg
31 rbb mficf bronj fox jumps overhehe lazy dyg
32 rbb mficf bronn fox jumps overhehe lazy dyg
33 rbb mficf bronn fox jumps over ehe lazy dyg
34 rhb mficf bronn fox jumps over ehe lazy dyg
35 hb mficf bronn fox jumps over ehe lazy dyg
36 hb mfick bronn fox jumps over ehe lazy dyg
37 hb m ick bronn fox jumps over ehe lazy dyg
38 hb m ick bronn fox jumps over ehe lazy dog
39 he m ick bronn fox jumps over ehe lazy dog
40 he m ick bronn fox jumps over the lazy dog
41 he q ick bronn fox jumps over the lazy dog
42 he q ick bronn fox jumps over the lazy dog
43 he q ick brown fox jumps over the lazy dog
44 he quick brown fox jumps over the lazy dog
45 ahe quick brown fox jumps over the lazy dog
46 the quick brown fox jumps over the lazy dog
As we see, each generation differs by no more than one symbol from each other. It took a total of 46 generations to get from rbbzmffwfhwtxnjjiozz ujhhlxeoyhezarquvmopyk to the quick brown fox jumps over the lazy dog through mutations and selection.
Classic experiments
Some examples, the Shakespearean line or the English pangram about the fox, are interesting, but not too convincing. Therefore, I decided to consider a more interesting question: what will happen if we take a couple of classical works, break them down into sentences and calculate the number of generations for each of them? What will be the nature of the dependence of the number of generations on the string (for example, on its length)?
I chose To Kill a Mocking Bird by Harper Lee (Kill a Mockingbird, Harper Lee) and Catcher in the Rye by JD Salinger (The Catcher in the Rye, JD Salinger) as classic works. We will measure two parameters - the distribution of the number of generations by sentences and the dependence of the number of generations on the length of the string (is there a correlation?).
The parameters were as follows: the number of descendants of the line: 100; the number of survivors in a generation: 10.
results
As we can see, for the majority of sentences it was possible to reach the line quickly enough, less than 100 iterations are required, almost iterations are enough for 200 iterations (among all the sentences there was only one that needed 1135 iterations, judging by the sentence, the breakdown algorithm made a mistake and glued several sentences into one ): The

correlation between string length and number of generations is perfect. This means that almost every generation managed to move one step closer to the target line.

R ^ 2 is 0.996 and 0.997 respectively.
Thus, it was experimentally established that under the conditions of our problem for any input string S , the number of generations linearly depends on the length of the string, which is consistent with the initial assumptions.
Code and data
All code, python - genetic algorithm \ text processing and R - visualization, available on github:
github.com/SergeyParamonov/genetics-experiments
conclusions
We figured out the basic structure of genetic algorithms and applied strings to solve the problem of mutation. As a result of experiments with classical texts, we found that in our conditions there is a linear relationship between the length of the string and the number of generations necessary to reach the input string.
We also noted that the basic search structure can be modified (for example, using crossover - using several generation members to create descendants) to solve a wide class of optimization problems where it is too difficult to find the exact solution.
