Histogram equalization to enhance image quality
Hello. Now, the supervisor and I are preparing a monograph for publication, where we are trying, in simple words, to talk about the basics of digital image processing. This article reveals a very simple, but at the same time very effective technique for improving image quality - equalization of histograms.
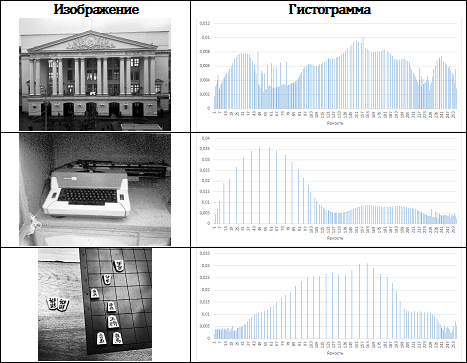
For simplicity, we begin our consideration with monochrome images (i.e., images containing information only about brightness, but not about the color of pixels). A histogram of an image will be called a discrete function H defined on a set of values [0; 2 bpp], where bpp is the number of bits allocated to encode the brightness of one pixel. Although this is not mandatory, the histograms are often normalized to the range [0; 1], dividing each value of the function H [i] by the total number of pixels in the image. In Tab. 1 shows examples of test images and histograms built on their basis:
Table. 1. Images and their histograms

Having carefully studied the corresponding histogram, we can draw some conclusions about the original image itself. For example, histograms of very dark images are characterized by the fact that nonzero histogram values are concentrated near zero brightness levels, and for very bright images, on the contrary, all nonzero values are concentrated on the right side of the histogram.
Intuitively, we can conclude that the most convenient for human perception will be an image in which the histogram is close to a uniform distribution. Those. To improve visual quality, an image must be transformed so that the histogram of the result contains all possible brightness values and at the same time in approximately the same amount. This conversion is called histogram equalization and can be done using the code in Listing 1.
Listing 1. Implementing the histogram equalization procedure
As a result of histogram equalization, in most cases the dynamic range of the image is significantly expanded, which allows you to display previously unnoticed details. This effect is especially pronounced in dark images, as shown in Table. 2. In addition, it is worth noting one more important feature of the equalization procedure: unlike most filters and gradation transformations that require setting parameters (aperture and gradation transform constants), histogram equalization can be performed in a fully automatic mode without operator intervention.
Tab. 2. Images and their histograms after equalization
It is easy to see that the histograms after equalization have peculiar noticeable gaps. This is due to the fact that the dynamic range of the output image is wider than the range of the original. Obviously, in this case, the mapping considered in Listing 1 cannot provide nonzero values in all pockets of the histogram. If, nevertheless, it is necessary to achieve a more natural appearance of the output histogram, you can use the random distribution of the values of the ith pocket of the histogram in its vicinity.
Obviously, the equalization of histograms makes it easy to improve the quality of monochrome images. Naturally, I want to apply a similar mechanism to color images.
Most not very experienced developers present the image in the form of three RGB color channels and try to apply the histogram equalization procedure to each color separately. In some rare cases, this makes it possible to succeed, but in most cases the result is so-so (the colors are unnatural and cold). This is due to the fact that the RGB model does not accurately display the color perception of a person.
Recall another color space - HSI. This color model (and others related to it) is very widely used by illustrators and designers as it allows you to operate with the more familiar concepts of color tone, saturation and intensity.
If we consider the projection of the RGB cube in the direction of the white-black diagonal, we get a hexagon, the corners of which correspond to primary and secondary colors, and all the gray shades (lying on the diagonal of the cube) are projected to the center point of the hexagon (see Fig. 1):
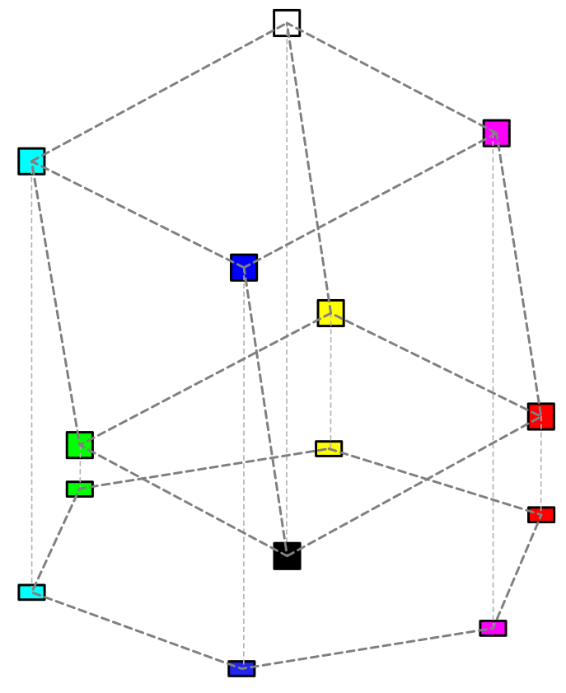
Fig. 1. Projection of the color cube
In order to use this model to encode all the colors available in the RGB model, it is necessary to add the vertical axis of lightness (or intensity) (I). The result is a hexagonal cone (Fig. 2, Fig. 3):
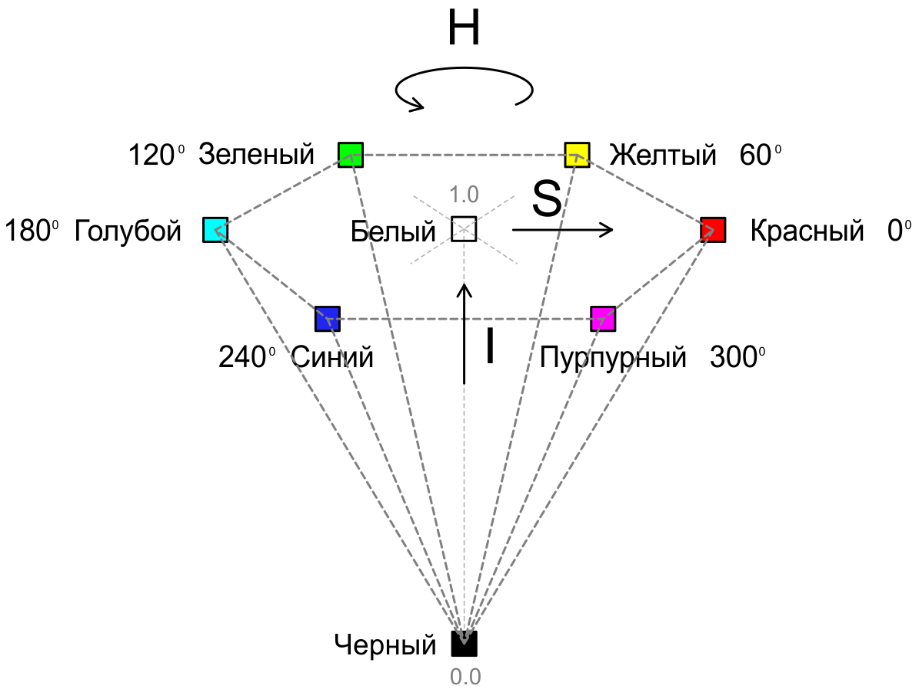
Fig. 2. HSI pyramid (tops)
In this model, the color tone (H) is set by the angle relative to the axis of red color, saturation (S) characterizes the purity of the color (1 means completely pure color, and 0 corresponds to a shade of gray). At zero saturation, the tone has no meaning and is not defined.

Fig. 3. The HSI Pyramid
in Tab. Figure 3 shows the decomposition of the image into HSI components (white pixels in the tone channel correspond to zero saturation):
Table. 3. HSI color space

It is believed that to improve the quality of color images, it is most effective to apply the equalization procedure to the intensity channel. This is exactly what is shown in Table. 4
tab. 4. Equalization of various color channels

I hope this material seemed to you at least interesting, as useful as possible. Thanks.
For simplicity, we begin our consideration with monochrome images (i.e., images containing information only about brightness, but not about the color of pixels). A histogram of an image will be called a discrete function H defined on a set of values [0; 2 bpp], where bpp is the number of bits allocated to encode the brightness of one pixel. Although this is not mandatory, the histograms are often normalized to the range [0; 1], dividing each value of the function H [i] by the total number of pixels in the image. In Tab. 1 shows examples of test images and histograms built on their basis:
Table. 1. Images and their histograms

Having carefully studied the corresponding histogram, we can draw some conclusions about the original image itself. For example, histograms of very dark images are characterized by the fact that nonzero histogram values are concentrated near zero brightness levels, and for very bright images, on the contrary, all nonzero values are concentrated on the right side of the histogram.
Intuitively, we can conclude that the most convenient for human perception will be an image in which the histogram is close to a uniform distribution. Those. To improve visual quality, an image must be transformed so that the histogram of the result contains all possible brightness values and at the same time in approximately the same amount. This conversion is called histogram equalization and can be done using the code in Listing 1.
Listing 1. Implementing the histogram equalization procedure
- procedure TCGrayscaleImage.HistogramEqualization;
- const
- k = 255;
- var
- h: array [0 .. k] of double;
- i, j: word;
- begin
- for i: = 0 to k do
- h [i]: = 0;
- for i: = 0 to self.Height - 1 do
- for j: = 0 to self.Width - 1 do
- h [round (k * self.Pixels [i, j])]: = h [round (k * self.Pixels [i, j])] + 1;
- for i: = 0 to k do
- h [i]: = h [i] / (self.Height * self.Width);
- for i: = 1 to k do
- h [i]: = h [i - 1] + h [i];
- for i: = 0 to self.Height - 1 do
- for j: = 0 to self.Width - 1 do
- self.Pixels [i, j]: = h [round (k * self.Pixels [i, j])];
- end;
As a result of histogram equalization, in most cases the dynamic range of the image is significantly expanded, which allows you to display previously unnoticed details. This effect is especially pronounced in dark images, as shown in Table. 2. In addition, it is worth noting one more important feature of the equalization procedure: unlike most filters and gradation transformations that require setting parameters (aperture and gradation transform constants), histogram equalization can be performed in a fully automatic mode without operator intervention.
Tab. 2. Images and their histograms after equalization

It is easy to see that the histograms after equalization have peculiar noticeable gaps. This is due to the fact that the dynamic range of the output image is wider than the range of the original. Obviously, in this case, the mapping considered in Listing 1 cannot provide nonzero values in all pockets of the histogram. If, nevertheless, it is necessary to achieve a more natural appearance of the output histogram, you can use the random distribution of the values of the ith pocket of the histogram in its vicinity.
Obviously, the equalization of histograms makes it easy to improve the quality of monochrome images. Naturally, I want to apply a similar mechanism to color images.
Most not very experienced developers present the image in the form of three RGB color channels and try to apply the histogram equalization procedure to each color separately. In some rare cases, this makes it possible to succeed, but in most cases the result is so-so (the colors are unnatural and cold). This is due to the fact that the RGB model does not accurately display the color perception of a person.
Recall another color space - HSI. This color model (and others related to it) is very widely used by illustrators and designers as it allows you to operate with the more familiar concepts of color tone, saturation and intensity.
If we consider the projection of the RGB cube in the direction of the white-black diagonal, we get a hexagon, the corners of which correspond to primary and secondary colors, and all the gray shades (lying on the diagonal of the cube) are projected to the center point of the hexagon (see Fig. 1):

Fig. 1. Projection of the color cube
In order to use this model to encode all the colors available in the RGB model, it is necessary to add the vertical axis of lightness (or intensity) (I). The result is a hexagonal cone (Fig. 2, Fig. 3):

Fig. 2. HSI pyramid (tops)
In this model, the color tone (H) is set by the angle relative to the axis of red color, saturation (S) characterizes the purity of the color (1 means completely pure color, and 0 corresponds to a shade of gray). At zero saturation, the tone has no meaning and is not defined.

Fig. 3. The HSI Pyramid
in Tab. Figure 3 shows the decomposition of the image into HSI components (white pixels in the tone channel correspond to zero saturation):
Table. 3. HSI color space

It is believed that to improve the quality of color images, it is most effective to apply the equalization procedure to the intensity channel. This is exactly what is shown in Table. 4
tab. 4. Equalization of various color channels

I hope this material seemed to you at least interesting, as useful as possible. Thanks.
