Persistent Queue
Inspired by the recent publication, “A persistent Cartesian tree by an implicit key,” I decided to write about the implementation of a persistent queue. Those who thought now that since the usual queue is a trivial structure, then its persistent version should be very simple, they were mistaken, the resulting implementation is at least no simpler than for the above tree.
We will implement, of course, the so-called full persistence - this means that the intermediate versions are available not only in read-only mode and we can add and extract elements from them at any time. In addition, we, of course, would like to have the same asymptotic behavior of the operating time and additional memory as for the non-persistent option, namely O (n), where n is the total number of operations performed with our queue. By the way, if we relax the requirements to O (n log n), then the queue is trivially emulated using a persistent Cartesian tree with an implicit key.
Let's take the following simple interface to work with our data structure: the version of the queues resulting from the requests will be numbered with non-negative integers, initially there is only an empty queue at number 0. Suppose we have N versions of the queues (including the original empty one), then they are numbered with numbers from 0 to N-1 and we can complete the following four queries:
As known, a persistent stack is a very simple data structure and its asymptotic behavior is what we need. In addition, we know that a queue can be simulated using two stacks. There is an obvious idea: we make these two stacks persistent and the problem is solved! Unfortunately, such a simple approach will not work. The thing is that with this simulation, not every operation has the asymptotics O (1): if during the pop'e the stack from which we get the elements turns out to be empty, then we transfer to it all the elements from another stack. In the case of a regular queue, each element is shifted only once, therefore, the total asymptotic behavior remains O (n), but in the persistent case, each element can belong to many queues and accordingly be shifted several times. Let, for example, q be the number of the queue for which this stack is empty, then after push (q, 1) and push (q, 2) for received queues, this stack will remain empty and when pop'e of them, each element of the queue q will be shifted twice. It is impossible to organize any joint use of the arranged elements due to the fact that the lowest elements of the stacks obtained by shifting will be different (1 and 2, respectively), and the persistent stack is arranged in such a way that each element stores a pointer to the element below it, therefore, in any case, we will be forced to have 2 copies of the penultimate element that will indicate the corresponding last, and therefore 2 copies of the penultimate to indicate the desired penultimate and so on in the chain . It is impossible to organize any joint use of the arranged elements due to the fact that the lowest elements of the stacks obtained by shifting will be different (1 and 2, respectively), and the persistent stack is arranged in such a way that each element stores a pointer to the element below it, therefore, in any case, we will be forced to have 2 copies of the penultimate element that will indicate the corresponding last, and therefore 2 copies of the penultimate to indicate the desired penultimate and so on in the chain . It is impossible to organize any joint use of the arranged elements due to the fact that the lowest elements of the stacks obtained by shifting will be different (1 and 2, respectively), and the persistent stack is arranged in such a way that each element stores a pointer to the element below it, therefore, in any case, we will be forced to have 2 copies of the penultimate element that will indicate the corresponding last, and therefore 2 copies of the penultimate to indicate the desired penultimate and so on in the chain .
Nevertheless, there is an algorithm based on such an idea (simulating a queue using two stacks), which guarantees that the stack that we get from pop'e will never be empty and uses 6 stacks to ensure this. My algorithm does not explicitly use this idea, although for general moments, of course, you can find it.
Let's try to use the same structure as when implementing the persistent stack: we will store the added elements in the form of a tree (more precisely, a set of trees - forests), at each vertex there will be an added element and a pointer to the one preceding it in the queue (more precisely, to the corresponding one the previous element is the top of the tree). Speaking in the future of the queue element, I will often mean exactly the vertex corresponding to the element.
A non-empty queue in this case can be represented by a pair of pointers to the first and last element of the queue, and the vertex corresponding to the first element will necessarily be the ancestor of the vertex corresponding to the last (well, or coincide with it in the case of a queue of one element). An example of such a structure and displaying a queue in it:
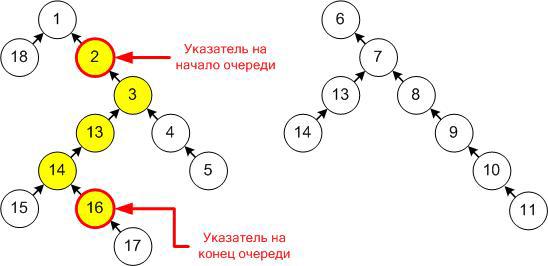
Note that the push operation simply creates a new vertex, setting it as the parent of the last element of the original queue (or it becomes the new root if added to the empty one), and the pop operation does not touch our forest at all, it simply moves the pointer to the first element. Thus, after creation, the vertex remains unchanged until the end of the work and you don’t have to worry that new operations can spoil existing queues in any way.
Our only problem with this approach is the implementation of the pop operation (the other three are trivial), it is not clear how to determine which vertex to move the pointer to the first element, because for the vertex we only store the pointer to the parent, but not to the sons (of which one vertex there may be several pieces, and even if all of them are stored, it is completely unclear which of them corresponds to the next element of our queue). Therefore, for each queue, in which there are more than two elements, we will additionally store a pointer to an element of some simply connected list, such that the list element according to our pointer contains a pointer to the second element of our queue, and the elements lying below it in the list, pointers to the third, fourth and so on respectively. Having such a pointer to the initial queue, when pop 'is executed
However, for reasons similar to those for which emulation of a queue by two stacks does not work, to ensure that for each queue below the list are absolutely all its intermediate vertices, we won’t succeed, therefore, let it only contain how many then the first of them, and when this list starts to get too small, we will build a new list, moving step by step (that is, increasing the list under construction by 1 element with each push or pop operation) from the end of the queue to the beginning, following the signs on the parents of the peaks of our tree but also trying to keep to the point where the old list is complete, we already had a new alert.
More formally, for each queue, in addition to pointers to the beginning and end and a pointer to an element of the finished list, we will also store a pointer to an element of the list under construction (in case we do not build anything, it will be 0) and calculate its value for the new queues (received after applying to the original push'a or pop'a) using the following simple algorithm:
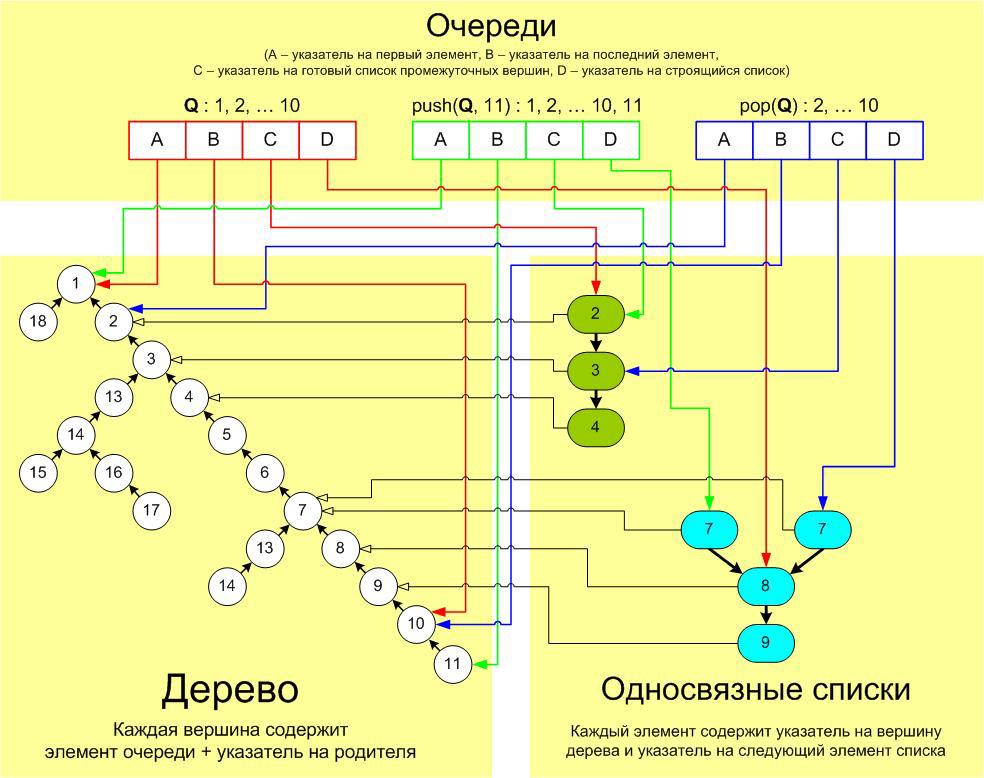
At the same time, we will not change the source element of the list itself, or the pointer to it stored for the initial queue, and in general, all data (tree tops, list items, data stored for queues) will be immutable (that is, after creation will never change their meaning). An image of how it all works and what happens when push'e or pop'e can be seen on the diagram (to make it more understandable did not work, no matter how hard I tried):
Accordingly, if upon completion of the list we reach the first intermediate element, then the construction for this queue is completed (while some other queues may continue to complete this list, but since the old elements never change, this will not harm us in any way). In this case, in place of the pointer to the element of the old list, write the pointer to the element of the new one, and assign the pointer to the constructed list to zero.
It can be seen from the description of the algorithm that during each request, we create no more than one new vertex of the tree and no more than one new list item and spend O (1) time, that is, the asymptotic behavior that we sought, and it remains only to discuss the correct criterion.
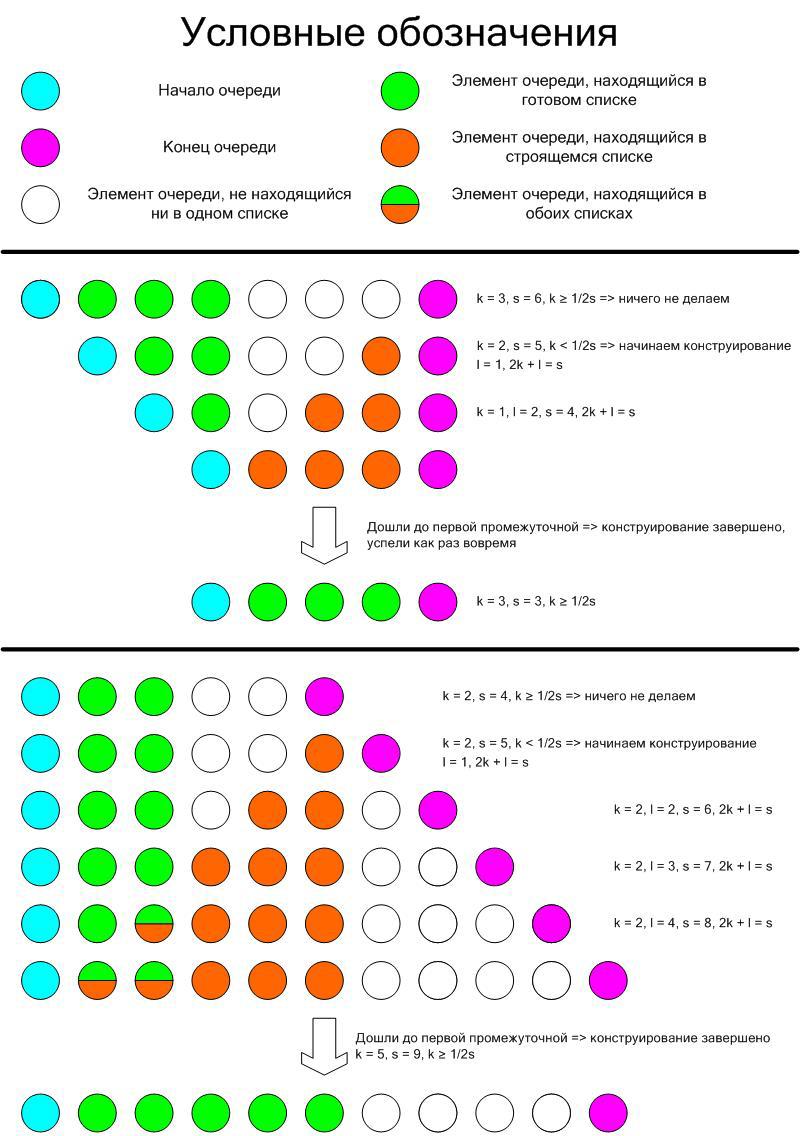
We will act as follows: while the size of our list is greater than or equal to 1/2 of the number of intermediate vertices (that is, vertices without the first and last), we do nothing, as soon as it becomes smaller, we begin to construct a new one. Note that if there are no intermediate vertices, then we have the inequality 0 ≥ 0 and do nothing, that is, in a special case, this is not necessary. We prove that with this approach we will never find ourselves in a situation where the old list is over and the new one is not ready yet.
To begin with, we prove the following invariant: if we construct a new list, then at each step 2k + l = s, where k is the number of elements in the old list, l is in the constructed list (after completion of construction completed at this step), s is the total number of intermediate elements. We will prove by the method of mathematical induction. Consider the first step when we just started construction (l = 1). Note that for the new queue 2k - s <0 (our criterion), however, for the original 2k old - s old ≥ 0. Let's see how this could happen: if our operation is push, then k = k old , and s = s old + 1, and if pop, then k = k old - 1 and s = s old - 1. As you can see, in both cases 2k - s is less than 2kold - s old is exactly one and, since both differences are integers, the second of them is 0, and the first is -1, therefore, 2k + 1 = s, and our l is just one. The induction base is proved. Let us prove the transition: let at some construction step 2k old + l old = s old . Then l = l old + 1 (completed the list with 1 element), in the case of push'a: k = k old , s = s old + 1, in the case of pop'a: k = k old - 1, s = s old - 1. In both cases, equality holds, which means the statement is proved.
Suppose now that we are doing the pop operation, and the initial list we need is empty (when pushing, we don’t use this list in any way). Then there may be one of two things:
It remains only to prove that when we finish the construction, the condition for the lack of construction is satisfied, that is, the length of the resulting list is not less than 1/2 of the total number of intermediate vertices, in other words, that at the time of completion 2l ≥ s or, equivalently, l ≥ s - l. But what is s - l? This is the number of intermediate vertices that are not in our list. It is easy to understand that it is equal to the number of push operations that occurred during the construction process. However, with each such operation, the number of elements in our list also increased by 1 (it is possible that in the previous step the element of the constructed list corresponds to the third element of the queue and we pop, then for the new queue the list element begins to correspond to the first intermediate element immediately without completion , but this is possible only at the last step of construction and only with the pop operation). Therefore, l ≥ the number of such push'eys (it is not difficult to understand that it is even strictly greater), which we needed to prove.
For clarity, we will demonstrate what happens in two extreme cases: when we always pop and when we push all the time:
Finally, I will give an implementation of the above data structure in C ++ (the implementation uses the innovations of C ++ 11). It is worth taking this code as a prototype, I tried to write it as simple and shorter as possible, sacrificing everything else to please it.
The types TreeNode, Queue, and QueueIntermediateTreeNodeList correspond to the top of the tree, queue, and element of the simply connected list from our algorithm. Boolean variables in Queue are used to correctly free memory in the destructor of our class: the top of the tree and the list item are deleted by the queue that created them (as was noted above, with each request no more than one vertex and no more than one list item is created). The top of the tree is created only during the push operation and the pointer to it is written to last, respectively, own_last indicates whether the new or old vertex is written to last. The list item created during construction is almost always written to constructing_intermediate_list, except when it was created and construction at the same step was completed, in which case it is transferred to known_intermediate_list,
The second possibly unobvious moment is the private member function manage_intermediate_lists, which looks like this:
This function implements the above algorithm for working with a pointer to a list under construction (note that the first three parameters are passed via a non-constant link, and for the first two it is assumed that the variables are initialized by the necessary values before the call). It is important to check before completing the list if the old element has become the first intermediate, because, as already noted, in the case of pop, this option is possible. Maybe someone noticed that we always check on our criterion for the start of construction:
Firstly, as you can see in the diagram , when several different operations are performed with the same queue for which construction is underway (these are pop (Q) and push (Q, 11) operations in the diagram), several elements are absolutely identical to each other list (they point to the same next element and the same vertex of the tree - in the diagram, these are two blue circles with the number 7). We could try to “glue” such elements into one, using, for example, a structure that, when completed, would tell us if someone had already done it before us (you can use a banal vector or a doubly linked list as such a structure). Obviously, such an optimization will work well (save a lot of memory) in the case of highly branched trees.
Secondly, we have another duplication: when the elements of the finished and under construction list point to the same vertex of the tree (we are talking about green-orange elements in this picture). Of course, we can’t avoid such duplication completely, because the lists may well have the same beginning and continuations that differ from each other, however, we could, when the first of the lists under construction reaches the end of the finished (rather than the beginning of the queue), simply “glue” it to this end, thereby saving a little memory. For the remaining lists (corresponding to this ready, of course), you still have to duplicate. Thus, this optimization will best manifest itself when we have a lot of long straight branches on the trees.
Finally, thirdly, you can try to play with the constants. For example, it is possible to complete in a step not by 1 element, but by 2, then it is enough to start construction at k <1 / 3s. Perhaps it will be somehow useful.
That's all, thanks to everyone who read it.
Formulation of the problem
We will implement, of course, the so-called full persistence - this means that the intermediate versions are available not only in read-only mode and we can add and extract elements from them at any time. In addition, we, of course, would like to have the same asymptotic behavior of the operating time and additional memory as for the non-persistent option, namely O (n), where n is the total number of operations performed with our queue. By the way, if we relax the requirements to O (n log n), then the queue is trivially emulated using a persistent Cartesian tree with an implicit key.
Let's take the following simple interface to work with our data structure: the version of the queues resulting from the requests will be numbered with non-negative integers, initially there is only an empty queue at number 0. Suppose we have N versions of the queues (including the original empty one), then they are numbered with numbers from 0 to N-1 and we can complete the following four queries:
- empty (query_id) - checks if the queue with the given number is empty;
- front (query_id) - returns the first element of the queue, while the queue itself does not change at all and no new queues are created. The operation is valid if the queue is not empty;
- push (query_id, new_element) - creates a new queue under number N, obtained by appending to the end of the original new element. The old version is still available under query_id;
- pop (query_id) - creates a new queue under number N, obtained by extracting the first element from the original. The original queue is still available under the old number. If the original queue was empty, the new one will also be empty.
Simulating a queue using stacks
For every problem there is a solution which is simple, fast, and wrong.
- The First Law of Online Judges
As known, a persistent stack is a very simple data structure and its asymptotic behavior is what we need. In addition, we know that a queue can be simulated using two stacks. There is an obvious idea: we make these two stacks persistent and the problem is solved! Unfortunately, such a simple approach will not work. The thing is that with this simulation, not every operation has the asymptotics O (1): if during the pop'e the stack from which we get the elements turns out to be empty, then we transfer to it all the elements from another stack. In the case of a regular queue, each element is shifted only once, therefore, the total asymptotic behavior remains O (n), but in the persistent case, each element can belong to many queues and accordingly be shifted several times. Let, for example, q be the number of the queue for which this stack is empty, then after push (q, 1) and push (q, 2) for received queues, this stack will remain empty and when pop'e of them, each element of the queue q will be shifted twice. It is impossible to organize any joint use of the arranged elements due to the fact that the lowest elements of the stacks obtained by shifting will be different (1 and 2, respectively), and the persistent stack is arranged in such a way that each element stores a pointer to the element below it, therefore, in any case, we will be forced to have 2 copies of the penultimate element that will indicate the corresponding last, and therefore 2 copies of the penultimate to indicate the desired penultimate and so on in the chain . It is impossible to organize any joint use of the arranged elements due to the fact that the lowest elements of the stacks obtained by shifting will be different (1 and 2, respectively), and the persistent stack is arranged in such a way that each element stores a pointer to the element below it, therefore, in any case, we will be forced to have 2 copies of the penultimate element that will indicate the corresponding last, and therefore 2 copies of the penultimate to indicate the desired penultimate and so on in the chain . It is impossible to organize any joint use of the arranged elements due to the fact that the lowest elements of the stacks obtained by shifting will be different (1 and 2, respectively), and the persistent stack is arranged in such a way that each element stores a pointer to the element below it, therefore, in any case, we will be forced to have 2 copies of the penultimate element that will indicate the corresponding last, and therefore 2 copies of the penultimate to indicate the desired penultimate and so on in the chain .
Nevertheless, there is an algorithm based on such an idea (simulating a queue using two stacks), which guarantees that the stack that we get from pop'e will never be empty and uses 6 stacks to ensure this. My algorithm does not explicitly use this idea, although for general moments, of course, you can find it.
Algorithm description
Let's try to use the same structure as when implementing the persistent stack: we will store the added elements in the form of a tree (more precisely, a set of trees - forests), at each vertex there will be an added element and a pointer to the one preceding it in the queue (more precisely, to the corresponding one the previous element is the top of the tree). Speaking in the future of the queue element, I will often mean exactly the vertex corresponding to the element.
A non-empty queue in this case can be represented by a pair of pointers to the first and last element of the queue, and the vertex corresponding to the first element will necessarily be the ancestor of the vertex corresponding to the last (well, or coincide with it in the case of a queue of one element). An example of such a structure and displaying a queue in it:

Note that the push operation simply creates a new vertex, setting it as the parent of the last element of the original queue (or it becomes the new root if added to the empty one), and the pop operation does not touch our forest at all, it simply moves the pointer to the first element. Thus, after creation, the vertex remains unchanged until the end of the work and you don’t have to worry that new operations can spoil existing queues in any way.
Our only problem with this approach is the implementation of the pop operation (the other three are trivial), it is not clear how to determine which vertex to move the pointer to the first element, because for the vertex we only store the pointer to the parent, but not to the sons (of which one vertex there may be several pieces, and even if all of them are stored, it is completely unclear which of them corresponds to the next element of our queue). Therefore, for each queue, in which there are more than two elements, we will additionally store a pointer to an element of some simply connected list, such that the list element according to our pointer contains a pointer to the second element of our queue, and the elements lying below it in the list, pointers to the third, fourth and so on respectively. Having such a pointer to the initial queue, when pop 'is executed
However, for reasons similar to those for which emulation of a queue by two stacks does not work, to ensure that for each queue below the list are absolutely all its intermediate vertices, we won’t succeed, therefore, let it only contain how many then the first of them, and when this list starts to get too small, we will build a new list, moving step by step (that is, increasing the list under construction by 1 element with each push or pop operation) from the end of the queue to the beginning, following the signs on the parents of the peaks of our tree but also trying to keep to the point where the old list is complete, we already had a new alert.
More formally, for each queue, in addition to pointers to the beginning and end and a pointer to an element of the finished list, we will also store a pointer to an element of the list under construction (in case we do not build anything, it will be 0) and calculate its value for the new queues (received after applying to the original push'a or pop'a) using the following simple algorithm:
- if the initial queue has this pointer equal to 0, we’ll check if it’s time for us to start building a new list (the criterion for such a check will be described below):
- if it’s time, then create a list item with a null pointer to the next one in the list (thereby this created item will be the end of the constructed list), and put the pointer to the top on the penultimate element of our queue (parent of the last item),
- if it’s not time yet, then leave the pointer equal to zero.
- In the case of a nonzero source pointer, we expand our list up one element: create a new element that points to the source as the next vertex in the list and to the parent corresponding to this source element.
At the same time, we will not change the source element of the list itself, or the pointer to it stored for the initial queue, and in general, all data (tree tops, list items, data stored for queues) will be immutable (that is, after creation will never change their meaning). An image of how it all works and what happens when push'e or pop'e can be seen on the diagram (to make it more understandable did not work, no matter how hard I tried):

Accordingly, if upon completion of the list we reach the first intermediate element, then the construction for this queue is completed (while some other queues may continue to complete this list, but since the old elements never change, this will not harm us in any way). In this case, in place of the pointer to the element of the old list, write the pointer to the element of the new one, and assign the pointer to the constructed list to zero.
It can be seen from the description of the algorithm that during each request, we create no more than one new vertex of the tree and no more than one new list item and spend O (1) time, that is, the asymptotic behavior that we sought, and it remains only to discuss the correct criterion.
Criterion for checking on the beginning of construction
We will act as follows: while the size of our list is greater than or equal to 1/2 of the number of intermediate vertices (that is, vertices without the first and last), we do nothing, as soon as it becomes smaller, we begin to construct a new one. Note that if there are no intermediate vertices, then we have the inequality 0 ≥ 0 and do nothing, that is, in a special case, this is not necessary. We prove that with this approach we will never find ourselves in a situation where the old list is over and the new one is not ready yet.
To begin with, we prove the following invariant: if we construct a new list, then at each step 2k + l = s, where k is the number of elements in the old list, l is in the constructed list (after completion of construction completed at this step), s is the total number of intermediate elements. We will prove by the method of mathematical induction. Consider the first step when we just started construction (l = 1). Note that for the new queue 2k - s <0 (our criterion), however, for the original 2k old - s old ≥ 0. Let's see how this could happen: if our operation is push, then k = k old , and s = s old + 1, and if pop, then k = k old - 1 and s = s old - 1. As you can see, in both cases 2k - s is less than 2kold - s old is exactly one and, since both differences are integers, the second of them is 0, and the first is -1, therefore, 2k + 1 = s, and our l is just one. The induction base is proved. Let us prove the transition: let at some construction step 2k old + l old = s old . Then l = l old + 1 (completed the list with 1 element), in the case of push'a: k = k old , s = s old + 1, in the case of pop'a: k = k old - 1, s = s old - 1. In both cases, equality holds, which means the statement is proved.
Suppose now that we are doing the pop operation, and the initial list we need is empty (when pushing, we don’t use this list in any way). Then there may be one of two things:
- or for the initial queue, we did not start constructing a new list, then this queue has 2k ≥ s,
k = 0 => s = 0, which means that it is a queue of size 0, 1 or 2 and knowing its last element to make pop'a is enough , - either started, then l ≠ 0, by virtue of the invariant 2k + l = s, k = 0 => l = s ≠ 0 => the constructed list was not empty and contained all the intermediate elements, which means that at that step we had to replace and get a non-empty list.
It remains only to prove that when we finish the construction, the condition for the lack of construction is satisfied, that is, the length of the resulting list is not less than 1/2 of the total number of intermediate vertices, in other words, that at the time of completion 2l ≥ s or, equivalently, l ≥ s - l. But what is s - l? This is the number of intermediate vertices that are not in our list. It is easy to understand that it is equal to the number of push operations that occurred during the construction process. However, with each such operation, the number of elements in our list also increased by 1 (it is possible that in the previous step the element of the constructed list corresponds to the third element of the queue and we pop, then for the new queue the list element begins to correspond to the first intermediate element immediately without completion , but this is possible only at the last step of construction and only with the pop operation). Therefore, l ≥ the number of such push'eys (it is not difficult to understand that it is even strictly greater), which we needed to prove.
For clarity, we will demonstrate what happens in two extreme cases: when we always pop and when we push all the time:

C ++ implementation
Finally, I will give an implementation of the above data structure in C ++ (the implementation uses the innovations of C ++ 11). It is worth taking this code as a prototype, I tried to write it as simple and shorter as possible, sacrificing everything else to please it.
persistent_queue.h
#ifndef PERSISTENT_QUEUE_H
#define PERSISTENT_QUEUE_H
#include
#include
using Element_type = int;
class Persistent_queue {
public:
Persistent_queue();
~Persistent_queue();
Persistent_queue(const Persistent_queue&) = delete;
Persistent_queue& operator =(const Persistent_queue&) = delete;
using Queue_id = size_t;
static const Queue_id start_queue_id = 0;
Queue_id push(Queue_id queue_id, const Element_type& value);
Queue_id pop(Queue_id queue_id);
const Element_type& front(Queue_id queue_id);
size_t size(Queue_id queue_id);
bool empty(Queue_id queue_id);
private:
struct TreeNode;
struct QueueIntermediateTreeNodeList;
struct Queue {
const TreeNode* const first;
const TreeNode* const last;
const size_t size;
const QueueIntermediateTreeNodeList* const known_intermediate_list;
const QueueIntermediateTreeNodeList* const constructing_intermediate_list;
const bool own_last;
const bool own_known_intermediate_list;
Queue(const TreeNode* const first, const TreeNode* const last, const size_t size,
const QueueIntermediateTreeNodeList* const known_intermediate_list,
const QueueIntermediateTreeNodeList* const constructing_intermediate_list,
const bool own_last, const bool own_known_intermediate_list);
~Queue() = default;
Queue(Queue&& source) = default; // needed for vector reallocation
Queue(const Queue&) = delete;
Queue& operator =(const Queue&) = delete;
};
std::vector queues_;
Queue_id register_new_queue(const TreeNode* const first, const TreeNode* const last,
const size_t size,
const QueueIntermediateTreeNodeList* const known_intermediate_list,
const QueueIntermediateTreeNodeList* const constructing_intermediate_list,
const bool own_last, const bool own_known_intermediate_list);
void manage_intermediate_lists(const QueueIntermediateTreeNodeList*& known_intermediate_list,
const QueueIntermediateTreeNodeList*& constructing_intermediate_list,
bool& own_known_intermediate_list, const TreeNode* const first, const TreeNode* const last,
const size_t size);
};
#endif // PERSISTENT_QUEUE_H
persistent_queue.cpp
#include "persistent_queue.h"
#include
struct Persistent_queue::TreeNode {
const TreeNode* const parent;
const Element_type element;
TreeNode(const TreeNode* const parent, const Element_type& value)
: parent(parent), element(value) {}
~TreeNode() = default;
TreeNode(const TreeNode&) = delete;
TreeNode& operator =(const TreeNode&) = delete;
};
struct Persistent_queue::QueueIntermediateTreeNodeList {
const Persistent_queue::TreeNode* const front;
const QueueIntermediateTreeNodeList* const next;
const size_t size;
QueueIntermediateTreeNodeList(const Persistent_queue::TreeNode* const front,
const QueueIntermediateTreeNodeList* const tail_list)
: front(front), next(tail_list), size{tail_list ? tail_list->size + 1 : 1} { assert(front); }
~QueueIntermediateTreeNodeList() = default;
QueueIntermediateTreeNodeList(const QueueIntermediateTreeNodeList&) = delete;
QueueIntermediateTreeNodeList& operator =(const QueueIntermediateTreeNodeList&) = delete;
};
Persistent_queue::Queue::Queue(
const Persistent_queue::TreeNode* const first, const Persistent_queue::TreeNode* const last,
const size_t size, const Persistent_queue::QueueIntermediateTreeNodeList* const known_intermediate_list,
const Persistent_queue::QueueIntermediateTreeNodeList* const constructing_intermediate_list,
const bool own_last, const bool own_known_intermediate_list
)
: first(first), last(last), size(size), known_intermediate_list(known_intermediate_list)
, constructing_intermediate_list(constructing_intermediate_list)
, own_last(own_last), own_known_intermediate_list(own_known_intermediate_list)
{
// Some asserts
if (size == 0) {
assert(first == nullptr);
assert(last == nullptr);
} else {
assert(first);
assert(last);
if (size > 1)
assert(last->parent);
}
if (size <= 2) {
assert(known_intermediate_list == nullptr);
assert(constructing_intermediate_list == nullptr);
if (size == 1)
assert(first == last);
if (size == 2)
assert(first == last->parent);
} else {
assert(known_intermediate_list);
assert(first == known_intermediate_list->front->parent);
}
}
size_t Persistent_queue::size(const Persistent_queue::Queue_id queue_id)
{
return queues_.at(queue_id).size;
}
bool Persistent_queue::empty(const Queue_id queue_id)
{
return size(queue_id) == 0;
}
const Element_type& Persistent_queue::front(const Persistent_queue::Queue_id queue_id)
{
assert(!empty(queue_id));
return queues_.at(queue_id).first->element;
}
Persistent_queue::Queue_id
Persistent_queue::register_new_queue(const TreeNode* const first, const TreeNode* const last,
const size_t size, const QueueIntermediateTreeNodeList* const known_intermediate_list,
const QueueIntermediateTreeNodeList* const constructing_intermediate_list,
const bool own_last, const bool own_known_intermediate_list)
{
queues_.emplace_back(first, last, size, known_intermediate_list, constructing_intermediate_list,
own_last, own_known_intermediate_list);
return queues_.size() - 1;
}
Persistent_queue::Persistent_queue()
{
register_new_queue(nullptr, nullptr, 0, nullptr, nullptr, false, false);
}
Persistent_queue::~Persistent_queue()
{
for (const auto& q : queues_) {
if (q.own_last)
delete q.last;
if (q.own_known_intermediate_list)
delete q.known_intermediate_list;
delete q.constructing_intermediate_list;
}
}
Persistent_queue::Queue_id
Persistent_queue::push(const Persistent_queue::Queue_id queue_id, const Element_type& value)
{
const auto& queue_for_push = queues_.at(queue_id);
const size_t size = queue_for_push.size + 1;
const bool own_last = true;
const TreeNode* first;
const TreeNode* last;
if (queue_for_push.size == 0) {
first = last = new TreeNode(nullptr, value);
} else {
first = queue_for_push.first;
last = new TreeNode(queue_for_push.last, value);
}
bool own_known_intermediate_list;
const QueueIntermediateTreeNodeList* known_intermediate_list = queue_for_push.known_intermediate_list;
const QueueIntermediateTreeNodeList* constructing_intermediate_list =
queue_for_push.constructing_intermediate_list;
manage_intermediate_lists(known_intermediate_list, constructing_intermediate_list,
own_known_intermediate_list, first, last, size);
return register_new_queue(first, last, size, known_intermediate_list, constructing_intermediate_list,
own_last, own_known_intermediate_list);
}
Persistent_queue::Queue_id Persistent_queue::pop(const Persistent_queue::Queue_id queue_id)
{
const auto& queue_for_pop = queues_.at(queue_id);
const bool own_last = false;
const TreeNode* first;
const TreeNode* last;
size_t size;
const QueueIntermediateTreeNodeList* known_intermediate_list;
if (queue_for_pop.size <= 1) {
first = last = nullptr;
size = 0;
known_intermediate_list = nullptr;
} else {
last = queue_for_pop.last;
size = queue_for_pop.size - 1;
if (queue_for_pop.size == 2) {
first = queue_for_pop.last;
known_intermediate_list = nullptr;
} else {
assert(queue_for_pop.known_intermediate_list != nullptr);
first = queue_for_pop.known_intermediate_list->front;
known_intermediate_list = queue_for_pop.known_intermediate_list->next;
}
}
bool own_known_intermediate_list;
const QueueIntermediateTreeNodeList* constructing_intermediate_list =
queue_for_pop.constructing_intermediate_list;
manage_intermediate_lists(known_intermediate_list, constructing_intermediate_list,
own_known_intermediate_list, first, last, size);
return register_new_queue(first, last, size, known_intermediate_list, constructing_intermediate_list,
own_last, own_known_intermediate_list);
}
void Persistent_queue::manage_intermediate_lists(
const Persistent_queue::QueueIntermediateTreeNodeList*& known_intermediate_list,
const Persistent_queue::QueueIntermediateTreeNodeList*& constructing_intermediate_list,
bool& own_known_intermediate_list, const Persistent_queue::TreeNode* const first,
const Persistent_queue::TreeNode* const last, const size_t size)
{
own_known_intermediate_list = false;
const size_t intermediate_nodes_count = (size > 2 ? size - 2 : 0);
size_t known_intermediate_list_size =
(known_intermediate_list ? known_intermediate_list->size : 0);
if (2*known_intermediate_list_size < intermediate_nodes_count) {
auto try_to_replace_known_to_constructing = [&](){
if (constructing_intermediate_list && constructing_intermediate_list->front->parent == first) {
known_intermediate_list = constructing_intermediate_list;
known_intermediate_list_size = constructing_intermediate_list->size;
constructing_intermediate_list = nullptr;
return true;
}
return false;
};
if (!try_to_replace_known_to_constructing()) {
const auto adding_node = (constructing_intermediate_list ?
constructing_intermediate_list->front->parent : last->parent);
constructing_intermediate_list = new QueueIntermediateTreeNodeList(
adding_node, constructing_intermediate_list);
if (try_to_replace_known_to_constructing())
own_known_intermediate_list = true;
}
}
// Check invariants
if (2*known_intermediate_list_size >= intermediate_nodes_count)
assert(constructing_intermediate_list == nullptr);
const size_t constructing_intermediate_list_size =
(constructing_intermediate_list ? constructing_intermediate_list->size : 0);
const auto invariant_sum = 2*known_intermediate_list_size + constructing_intermediate_list_size;
assert(invariant_sum >= intermediate_nodes_count);
if (constructing_intermediate_list)
assert(invariant_sum == intermediate_nodes_count);
}
The types TreeNode, Queue, and QueueIntermediateTreeNodeList correspond to the top of the tree, queue, and element of the simply connected list from our algorithm. Boolean variables in Queue are used to correctly free memory in the destructor of our class: the top of the tree and the list item are deleted by the queue that created them (as was noted above, with each request no more than one vertex and no more than one list item is created). The top of the tree is created only during the push operation and the pointer to it is written to last, respectively, own_last indicates whether the new or old vertex is written to last. The list item created during construction is almost always written to constructing_intermediate_list, except when it was created and construction at the same step was completed, in which case it is transferred to known_intermediate_list,
The second possibly unobvious moment is the private member function manage_intermediate_lists, which looks like this:
void Persistent_queue::manage_intermediate_lists(
const Persistent_queue::QueueIntermediateTreeNodeList*& known_intermediate_list,
const Persistent_queue::QueueIntermediateTreeNodeList*& constructing_intermediate_list,
bool& own_known_intermediate_list, const Persistent_queue::TreeNode* const first,
const Persistent_queue::TreeNode* const last, const size_t size)
{
own_known_intermediate_list = false;
const size_t intermediate_nodes_count = (size > 2 ? size - 2 : 0);
size_t known_intermediate_list_size =
(known_intermediate_list ? known_intermediate_list->size : 0);
if (2*known_intermediate_list_size < intermediate_nodes_count) {
auto try_to_replace_known_to_constructing = [&](){
if (constructing_intermediate_list && constructing_intermediate_list->front->parent == first) {
known_intermediate_list = constructing_intermediate_list;
known_intermediate_list_size = constructing_intermediate_list->size;
constructing_intermediate_list = nullptr;
return true;
}
return false;
};
if (!try_to_replace_known_to_constructing()) {
const auto adding_node = (constructing_intermediate_list ?
constructing_intermediate_list->front->parent : last->parent);
constructing_intermediate_list = new QueueIntermediateTreeNodeList(
adding_node, constructing_intermediate_list);
if (try_to_replace_known_to_constructing())
own_known_intermediate_list = true;
}
}
// Check invariants
}
This function implements the above algorithm for working with a pointer to a list under construction (note that the first three parameters are passed via a non-constant link, and for the first two it is assumed that the variables are initialized by the necessary values before the call). It is important to check before completing the list if the old element has become the first intermediate, because, as already noted, in the case of pop, this option is possible. Maybe someone noticed that we always check on our criterion for the start of construction:
if (2*known_intermediate_list_size < intermediate_nodes_count) {Possible optimizations
Firstly, as you can see in the diagram , when several different operations are performed with the same queue for which construction is underway (these are pop (Q) and push (Q, 11) operations in the diagram), several elements are absolutely identical to each other list (they point to the same next element and the same vertex of the tree - in the diagram, these are two blue circles with the number 7). We could try to “glue” such elements into one, using, for example, a structure that, when completed, would tell us if someone had already done it before us (you can use a banal vector or a doubly linked list as such a structure). Obviously, such an optimization will work well (save a lot of memory) in the case of highly branched trees.
Secondly, we have another duplication: when the elements of the finished and under construction list point to the same vertex of the tree (we are talking about green-orange elements in this picture). Of course, we can’t avoid such duplication completely, because the lists may well have the same beginning and continuations that differ from each other, however, we could, when the first of the lists under construction reaches the end of the finished (rather than the beginning of the queue), simply “glue” it to this end, thereby saving a little memory. For the remaining lists (corresponding to this ready, of course), you still have to duplicate. Thus, this optimization will best manifest itself when we have a lot of long straight branches on the trees.
Finally, thirdly, you can try to play with the constants. For example, it is possible to complete in a step not by 1 element, but by 2, then it is enough to start construction at k <1 / 3s. Perhaps it will be somehow useful.
That's all, thanks to everyone who read it.
