Persistent Cartesian tree by implicit key
Caution persistence
Today is a rather unusual day, isn't it? How often do articles about persistent data structures appear on Habré? And today I want to tell you about the undeservedly forgotten persistent deramide by implicit key. So, let's begin.
1. What does the author mean by persistence?
According to the source of knowledge , a persistent data structure is a data structure that stores information about all of its previous versions when operations of its change occurred.
There are several options for how to make the data structure persistent. In this case, we will create a completely persistent data structure by copying only those vertices at which something has changed. Thus, we do not need to somehow change the structure of ordinary deramide or completely copy the entire tree with any change. Good? Of course!
2. How to do this?
Consider the usual implicit key deramide structure. In order not to be unfounded, we will consider the amount on the segment.
struct PersistentTreap
{
int size;
long long sum, key;
PersistentTreap *left, *right;
//сюда будут добавлены еще переменные
PersistentTreap()
{
left = NULL;
right = NULL;
key = sum = 0;
size = 0;
}
PersistentTreap(int x)
{
left = right = NULL;
sum = key = x;
size = 1;
link = 0;
}
//И это тоже еще не все
};
typedef PersistentTreap* PtrPersistentTreap;
int getSize(PtrPersistentTreap root)
{
if (!root)
return 0;
return root->size;
}
long long getSum(PtrPersistentTreap root)
{
if (!root)
return 0;
return root->sum;
}
void addLink(PtrPersistentTreap root)
{
if (!root)
return;
root->link++;
}
void update(PtrPersistentTreap root)
{
if (!root)
return;
root->size = 1 + getSize(root->left) + getSize(root->right);
root->sum = root->key + getSum(root->left) + getSum(root->right);
}
As you can see, this is a rather trivial part of the code, which is known to everyone who at least once wrote a deramid by an implicit key. Now let's move on to the most interesting: how to make split, merge and push operations (as an option) not irreversibly change the structure of the tree?
Consider a few pictures to help us figure this out.
The original Cartesian tree before the split operation. (the vertices indicate the numbers that correspond to them in the array). That is, it is similar to an array
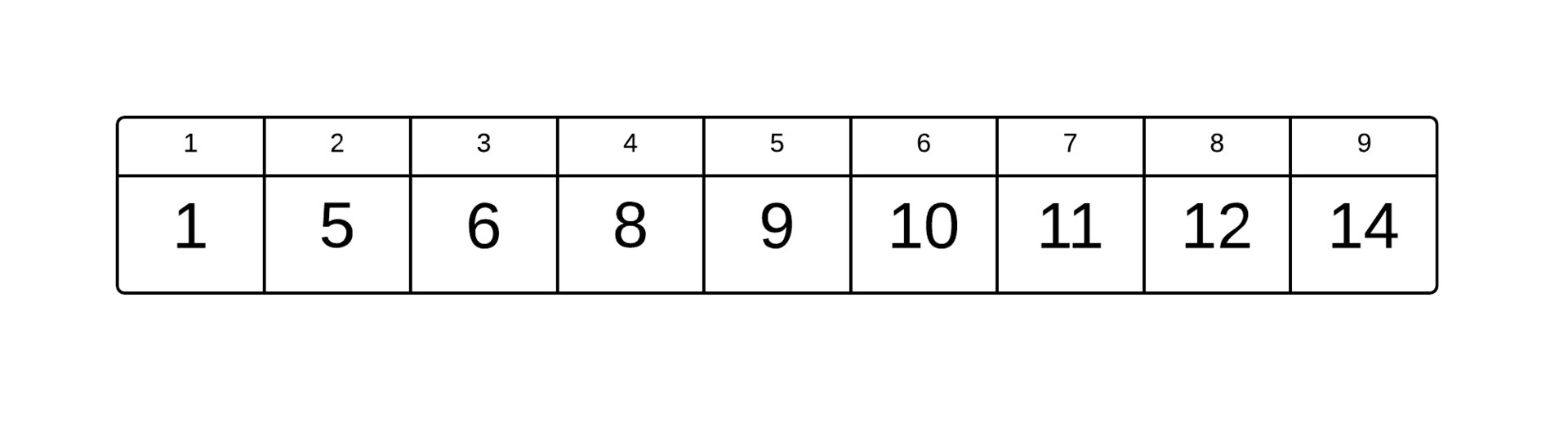 .
. 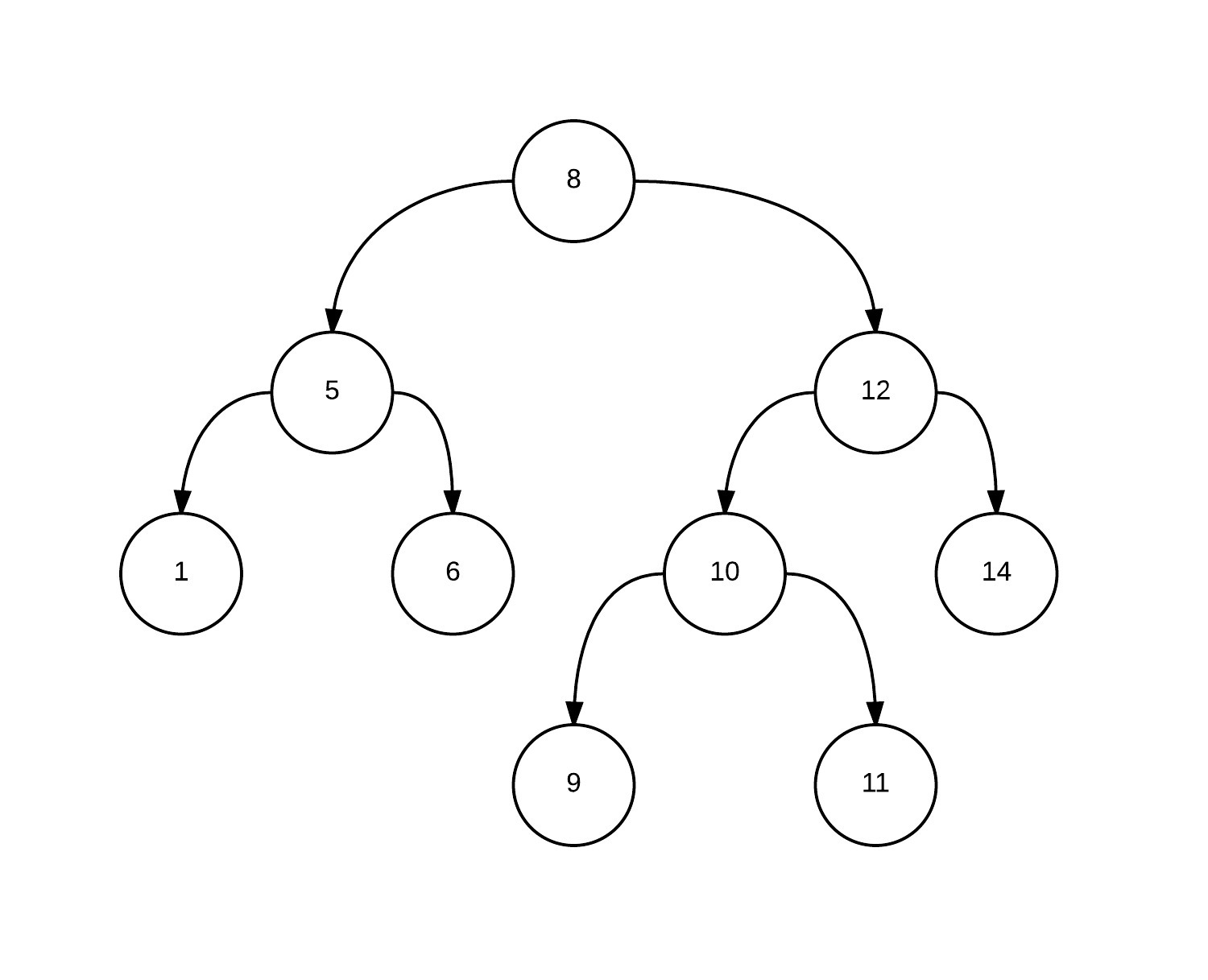
After the persistent split operation, in which we requested 5 elements in the right tree, we get the next forest. Blue denotes the vertices of the original deramide, green - created new vertices. Dotted arrows indicate connections between new vertices.
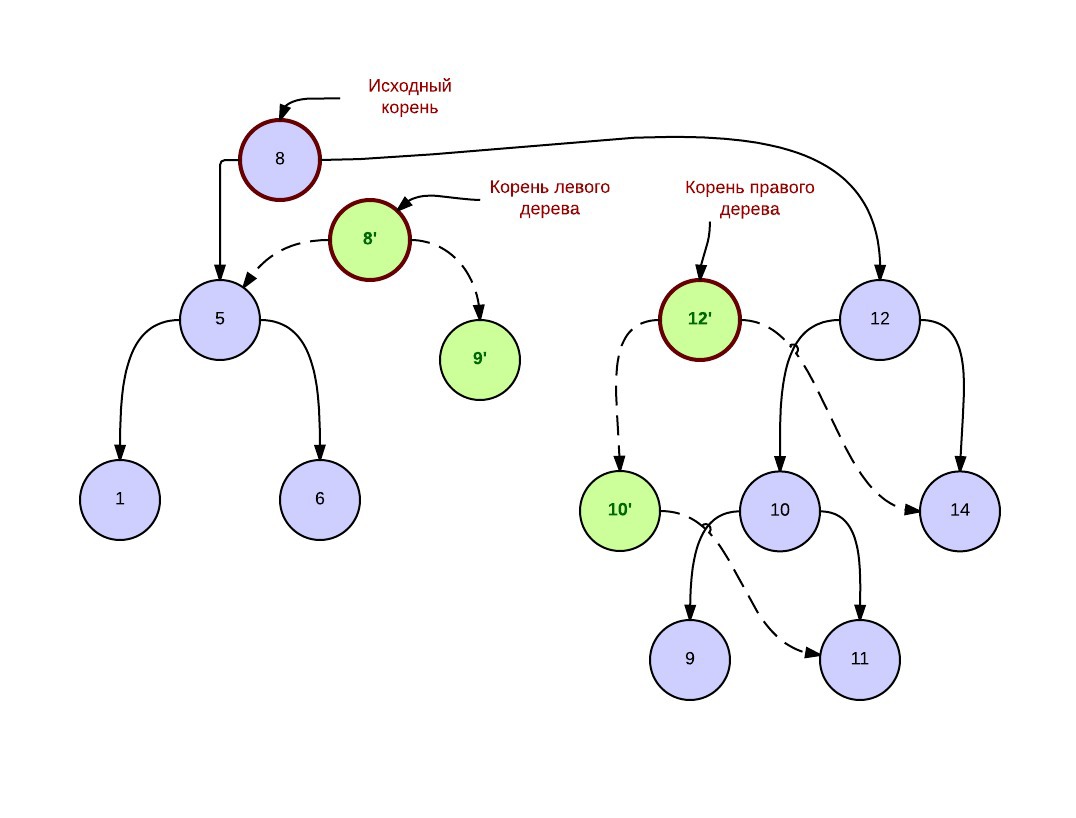
So, with every recursive call to the split operation, we do not have the right to modify the existing tree in any way, we need to create a new vertex that is exactly a copy of this one and carry out all the change operations only with it. Literally this is what we will write. To do this, we will first create a copy constructor:
PersistentTreap(PersistentTreap* cur)
{
if (!cur)
{
return;
}
left = cur->left;
right = cur->right;
sum = cur->sum;
key = cur->key;
size = cur->size;
}That's it, now you can write a persistent version of the split operation. Its only difference with the usual one is that we simply copy the root we want to change and continue to do our usual work.
void Split(PtrPersistentTreap root, PtrPersistentTreap &L, PtrPersistentTreap &R, int size)
{
if (!root)
{
L = R = NULL;
return;
}
PtrPersistentTreap cur = new PersistentTreap(root);
if (getSize(cur->left) + 1 <= size)
{
split(cur->right, cur->right, R, size - getSize(cur->left) - 1);
L = cur;
}
else
{
split(cur->left, L, cur->left, size);
R = cur;
}
update(L);
update(R);
}
Great, a third of all the work is done. Now you need to deal with the persistent operation merge. Consider two deramides that were obtained in some way (again, consider that everything is obtained from the original array). For the merge operation to work correctly, assign them priorities so that the maximum is in the root (highlighted in red in brackets). It will be shown later that they are not really needed for the algorithm to work properly.
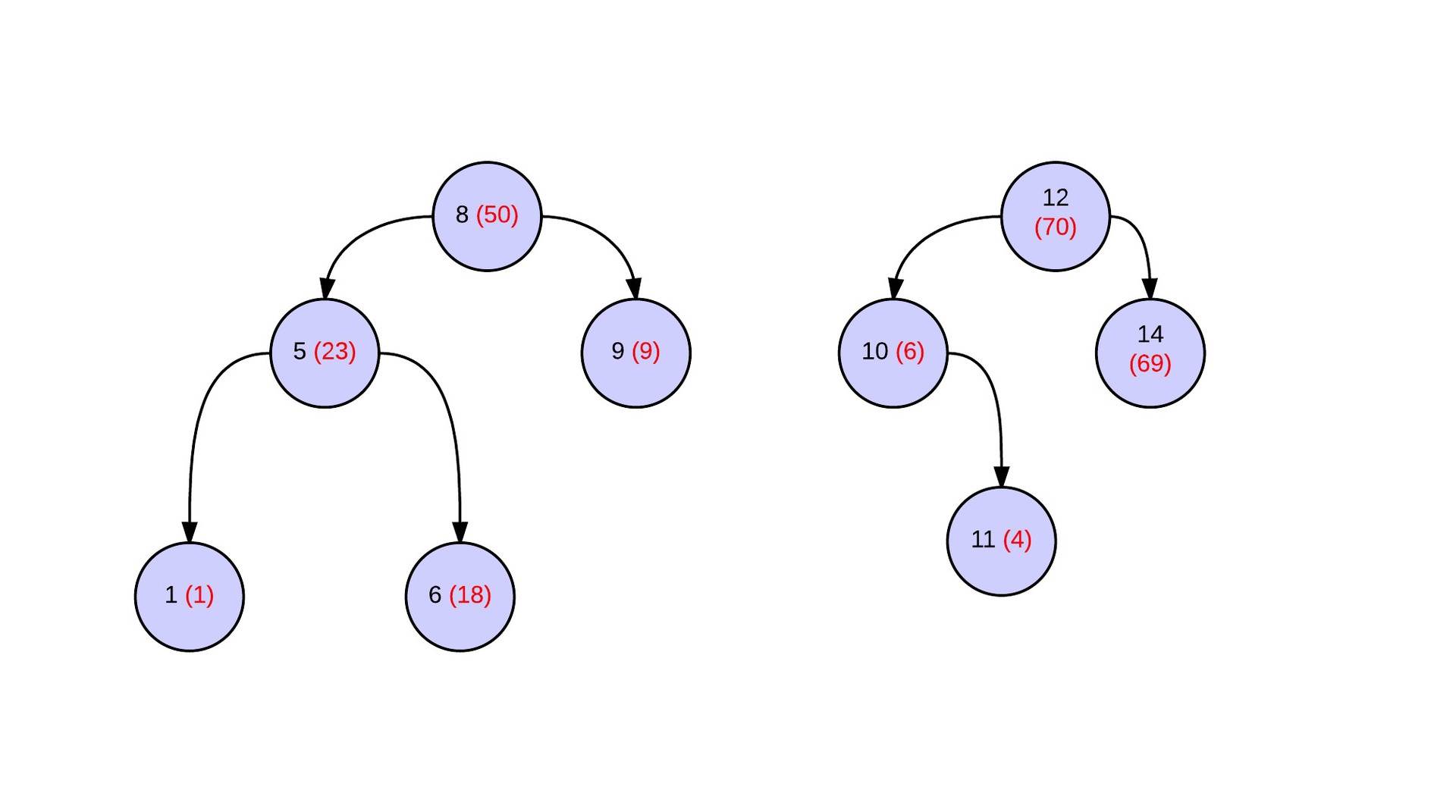
The result of the merge operation is a deramide in which heap properties are executed for vertex priorities. Below is a picture of the tree after the merge operation. Blue denotes the vertices of the original deramide, green - created new vertices. Dotted arrows indicate connections between new vertices.
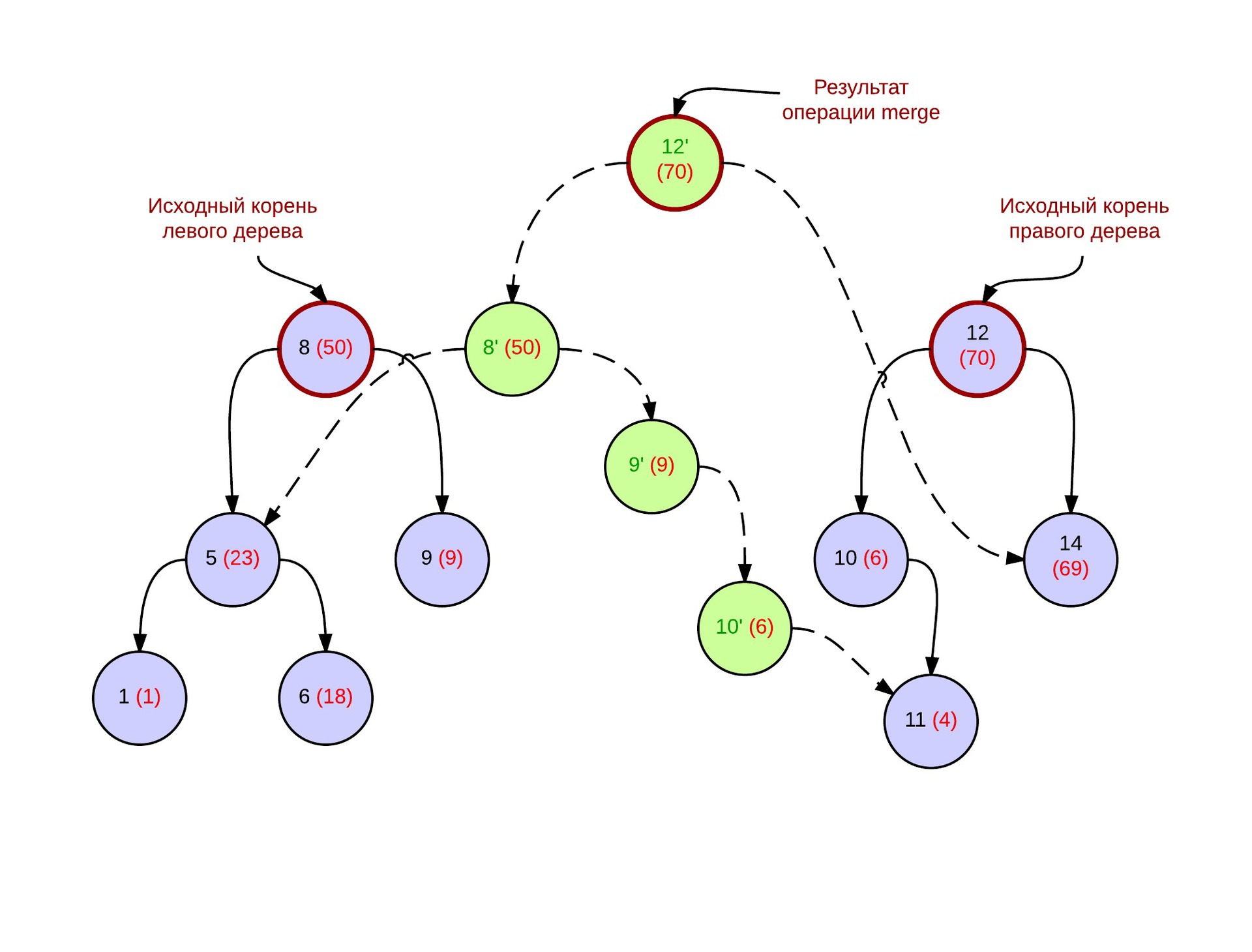
In our implementation, we will require merge to return a pointer to a new vertex of the tree. Thus, on each call, we copy the vertex, which will become the root, and change her pointer to one of her sons. Which one depends on whether it was a left or right tree.
PtrPersistentTreap Merge(PtrPersistentTreap L, PtrPersistentTreap R)
{
PtrPersistentTreap ptrNode = NULL;
if (!L || !R)
{
ptrNode = new PersistentTreap((!L ? R : L));
return ptrNode;
}
if (L->prior > R->prior)
{
ptrNode = new PersistentTreap(L);
ptrNode->right = Merge(L->right, R);
update(ptrNode);
return ptrNode;
}
else
{
ptrNode = new PersistentTreap(R);
ptrNode->left = Merge(L, R->left);
return ptrNode;
}
}However, it was promised that at the vertices there is absolutely no need to store a whole field prior, now I will tell you how to get rid of it (extremely useful for a persistent implementation). Indeed, if priorities coincide, the tree can degenerate into an ordinary bamboo, which reduces its benefits immediately to nothing. To set a new priority for each call to the top is an expensive pleasure, not the fact that it doesn’t exactly coincide with any other, and not the fact that the structure of the tree will be preserved. It turns out there is a simple and elegant solution.
Each vertex of the deramide stores the size of the tree that it represents. So with this value you can try to connect the priority of the vertex in order to become the root. It’s logical enough to make sure that the priority of the vertex, which has a larger tree, is greater. Let us prove now that in this case each vertex has the same probability of becoming the root of the tree. We do this by induction. Suppose we want to choose a root of two vertices. Obviously, the probabilities of becoming the root for them are equal. Now consider the case when we have only L vertices in the left tree and R. in the right tree. Then, according to the algorithm, a vertex from the left tree can become a root with probability
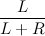 . But each vertex the top of the tree L could become a root with probability
. But each vertex the top of the tree L could become a root with probability  . So each vertex of the tree L can become a root with probability
. So each vertex of the tree L can become a root with probability . The case for the right tree is considered similarly. That's it, the transition is proved, since the probabilities for all vertices are the same.
. The case for the right tree is considered similarly. That's it, the transition is proved, since the probabilities for all vertices are the same. So in the merge operation instead
if (L->prior > R->prior)int l = getSize(L), r = getSize(R), rang = rand() % (l + r);
if (rang > r)3. Adds a reference count to the top.
Hooray, the bulk of the persistent data structure is written. The following changes that need to be made are the implementation of reference counting. To do this, add the link field, which is responsible for storing the number of vertices that reference this one. It is logical to assume that if this field is not empty, then we can by no means just delete the current vertex, because this will somehow affect the remaining versions of the tree. And yes, when deleting a vertex, we also reduce the link in its children and cause recursive deletion, if required.
The split and merge operations with this addition and the addition of the tree structure itself
struct PersistentTreap
{
short link;
int size;
long long sum, key;
PersistentTreap *left, *right;
PersistentTreap()
{
left = NULL;
right = NULL;
key = sum = 0;
size = 0;
link = 0;
}
PersistentTreap(PersistentTreap* cur)
{
if (!cur)
{
return;
}
left = cur->left;
right = cur->right;
sum = cur->sum;
key = cur->key;
size = cur->size;
link = 0;
}
PersistentTreap(int x)
{
left = right = NULL;
sum = key = x;
size = 1;
link = 0;
}
void del()
{
link--;
if (link <= 0)
{
if (left != NULL)
left->del();
if (right != NULL)
right->del();
delete this;
}
}
};
void addLink(PtrPersistentTreap root)
{
if (!root)
return;
root->link++;
}
void DelNode(PtrPersistentTreap root)
{
if (!root)
return;
root->del();
}
void Split(PtrPersistentTreap root, PtrPersistentTreap &L, PtrPersistentTreap &R, int size)
{
if (!root)
{
L = R = NULL;
return;
}
PtrPersistentTreap cur = new PersistentTreap(root);
if (getSize(cur->left) + 1 <= size)
{
Split(cur->right, cur->right, R, size - getSize(cur->left) - 1);
addLink(cur->left);
addLink(cur->right);
L = cur;
}
else
{
Split(cur->left, L, cur->left, size);
addLink(cur->left);
addLink(cur->right);
R = cur;
}
update(L);
update(R);
}
PtrPersistentTreap Merge(PtrPersistentTreap L, PtrPersistentTreap R)
{
PtrPersistentTreap ptrNode = NULL;
if (!L || !R)
{
ptrNode = new PersistentTreap((!L ? R : L));
addLink(ptrNode->left);
addLink(ptrNode->right);
return ptrNode;
}
int l = getSize(L), r = getSize(R), rang = rand() % (l + r);
if (rang > r)
{
ptrNode = new PersistentTreap(L);
ptrNode->right = Merge(ptrNode->right, R);
addLink(ptrNode->left);
addLink(ptrNode->right);
update(ptrNode);
return ptrNode;
}
else
{
ptrNode = new PersistentTreap(R);
ptrNode->left = Merge(L, ptrNode->left);
addLink(ptrNode->left);
addLink(ptrNode->right);
update(ptrNode);
return ptrNode;
}
}
Now we can rightfully say that we finally wrote the persistent deramide using an implicit key. Why do we need it? It can do exactly the same operations as an ordinary implicit key deramide, but unlike it, now we can copy pieces of the array, paste copies of the pieces of the array back into the array, without fear of matching priorities or increasing communication time with a complete copy of the deramide . An example of using persistent deramide.
