Cellular Machine Steppers
This article proposes the rules for a two-dimensional cellular automaton, which, on the one hand, is very similar to the game Conway's Game of Life , and on the other hand, has significant differences. First of all, it is distinguished by an increased up to three number of cell states, an increased ability to self-organization, an unlimited time of active evolution and an unlimited number of moving configurations.
For stable configurations, the new rules coincide with the rules of the Life game, therefore, all stable configurations in the Life game exist in the new rules. In the described cellular automaton there is a large class of moving configurations, spaceships. All these configurations move along the same progressive mechanism, which resembles the movement of a stepper excavator and a person on crutches. I called such spaceships a stepper , and the Steppers rule itself. So we will call it in the future.
There are quite a few oscillators in Steppers, and some oscillators from the game Life work in Steppers, which indicates the continuity of the rules. And finally, the famous Conway glider also exists in the proposed rules. The article will consider the dynamics of randomly filled gratings, reveal the mechanism of movement of the steppers, describe the currently found oscillators and steppers. Examples of collisions and complex functional behavior will also be given.

[00] An example of a moving configuration generating a stream of steppers
In 1988, I worked in a laboratory for technical vision. Studying the algorithm of skeletonization of a raster monochrome image, I wrote a program for its implementation. The skeletonization algorithm itself was never useful to us and was abandoned, and the program we wrote turned out to be a pretty decent cellular automaton with a graphical editor and graphical output after a little refinement. The first test for her, of course, was the game Life of John Conway. After a while, I wanted to experiment with other rules, and I remembered the article I read earlier, " Evolution of the game Evolution"in the journal" Science and Life "for 1975 [1]. In this article, trying to develop the game Life, the author I. Sidorov added a third state for newly born cells. Under the new rules, a cell can be in three states, empty, young and old. A young cell does not die under any circumstances, and in the next generation becomes old.

[01] Designation of cell conditions
I. Sidorov formulated all the rules completely in the following form:
There are two ships described by him in I. Sidorov’s cellular automaton. Later I managed to find two oscillators. Unfortunately, when a certain critical mass is exceeded, the population loses its structure and grows rapidly. Since it was not interesting to observe this, I undertook to develop my own laws of life and death.
After selecting various options, the following rules were formed:
More clearly, the rules can be presented in the form of tables. The axes show the number of young and old neighbors.
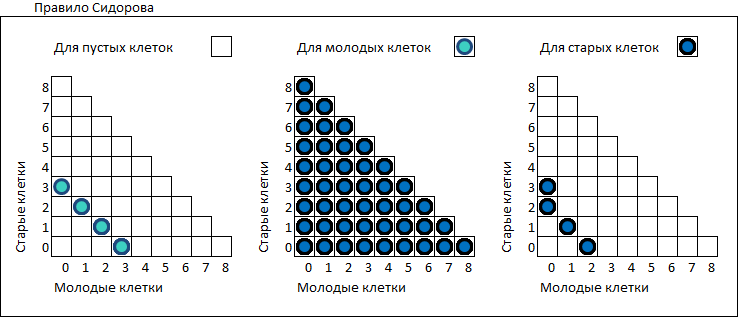
[02] Tabular presentation of the rule I. Sidorov
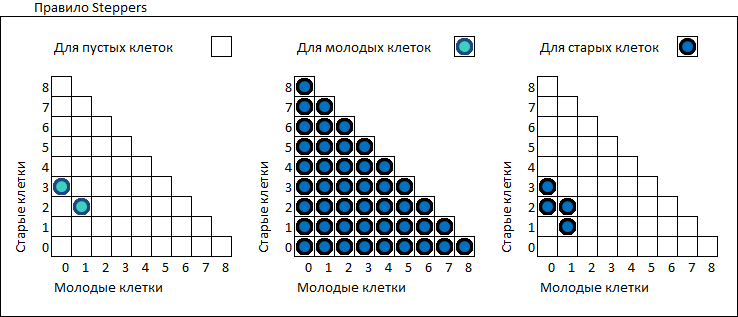
[03] Tabular presentation of the rule Steppers
This rule seemed so interesting to me that I wrote my article and sent it to the same journal, Science and Life. After some time, I received an answer that in the near future publications on cellular automata are not planned. For more than twenty years, I slowly, with large interruptions, worked on this cellular automaton, but made no attempt to publish it anywhere. And only with the advent of the wonderful Golly program, in which you can create cellular automata according to arbitrary rules, did the opportunity to share your modest research appear. Golly is free and can be downloaded from http://sourceforge.net/projects/golly/ .
All illustrations in this article are indexed, if desired, you can download the MilhinSA.Golly2.5.zip archivein which rle-files with all examples are located under the corresponding index. In this case, you can not be content with static pictures, but see the process in action. Golly can open this archive with the rule and examples without first unpacking it.
In March 2012, I posted a post about Steppers cellular machine at the Conway's Game of Life English forum . The message aroused some interest among the forum participants, some of them took part in the Steppers study and shared their findings.
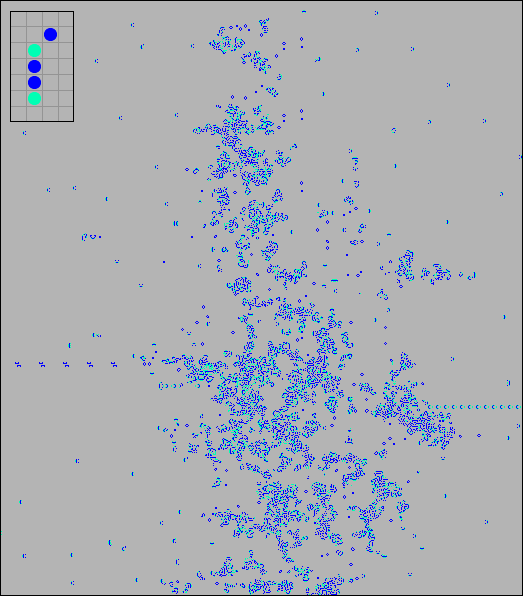
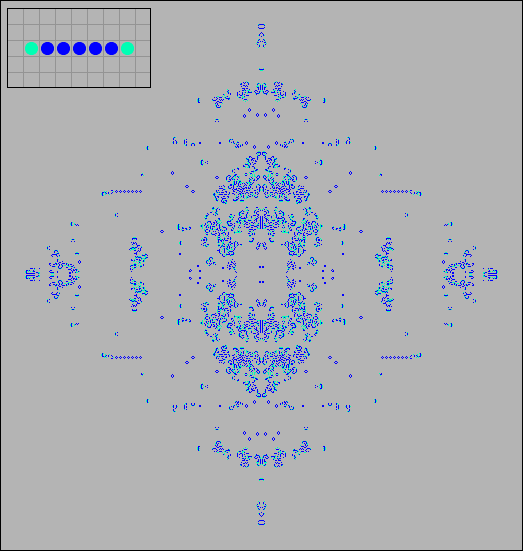
The best way to check the integral characteristics of a cellular automaton is to send a noise signal, or, in other words, a randomly populated population to its input. The following figure shows the evolution of a randomly filled toroidal grid of the game Life and Steppers in generations 32, 320, and 3200. It can be seen that the population density of Steppers decreases more slowly than in the game Life and stabilizes at some stage.

[04] Evolution of a random population of the game Life and Steppers
To obtain statistically reliable data, the following computational experiment was conducted. For each rule, a randomly filled toroidal field of 256 x 256 cells with a density of 50% was formed. The cellular machine worked out up to 10,000 generations. For each generation, the field density was calculated as a percentage, as well as the percentage of cells that changed their state. The last parameter characterizes the activity of the cellular automaton. For each machine, this process was repeated 1000 times, then the output was averaged.
Below are graphs of density and activity. From these graphs it can be seen that the density and, accordingly, the activity of the game Life quickly drops at the very beginning of development and in the 3000-4000 generation decreases on average to 3% of the density. Activity drops to an average of 1%. It is easy to understand that these are the remaining stationary configurations and simple oscillators. The cellular machine Steppers evolves in a different scenario. For about 20 generations, a balance has been established between young and old cells, which leads to a damped oscillatory process. Then the density begins to decrease, and in the 500-700 generation it stabilizes by 21%. Activity stabilizes by 14%. Thus, the evolution of a random field of sufficient size continues indefinitely.
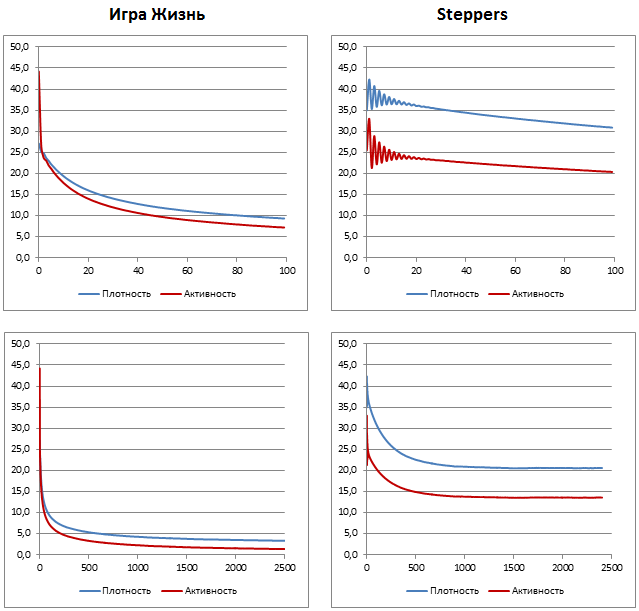
[05] Graphs of changes in density and activity
Graphs of changes in density and activity show the average value for the entire field, but the density and activity of cells changes not only in time but also in space. During the evolution of a uniformly filled random field, it can be seen that the cells are grouped into active regions, forming some texture. To highlight areas with increased activity, a special cellular automaton mapping algorithm was applied. It works as follows. For each cell over 32 generations, the number of births and deaths is calculated. Then the image of the cellular automaton in the black-red-yellow-white palette is displayed. The following figure shows that the active cells in the game Life quite quickly break up into isolated areas, which subsequently die out. In the Steppers cellular machine, the active areas are constantly changing shape and size, merge and disintegrate. Sufficiently large areas remain free and there are hospitals, oscillators, as well as gliders and steppers. Due to this, even with the evolution of a random field, a rather interesting picture arises as a result of self-organization, which is interesting to observe.

[06] Change in population activity during evolution
It should be recognized that the Stepper rule is not only very tenacious, but also very explosive. Often, the interaction of simple configurations leads to uncontrollable population growth. On the Conway's Game of Life forum , minimum size configurations were found that caused unlimited population growth. The following figure depicts a 5-cell pattern, as well as its state in the 1500 generation, and not completely. The population size is slightly less than 20,000 cells.
[07] The 5-cell pattern in the 1500th generation The
linear 7-cell pattern is developing even more intensively. Here he is depicted in the 500th generation, the population size of 8 124 cells. In the 3000 generation, the population size will exceed 500,000 cells.
[08] 7-cell pattern in the 500th generation
In the Steppers cellular automaton, at the moment, two types of moving configurations are found. Moreover, the only type refers to the first type, which is called the glider in the game Life. It is seen that the glider in Steppers is very slightly different from the glider from the game Life. With such a significant difference between these rules, the existence of gliders was rather unexpected.
[09] Comparison of the gliders of the game Life and Steppers
The steppers belong to another type, and their number is unlimited, since their size is unlimited. All steppers are united in the same way of movement. And this method owes its existence to the birth rule. Let me remind you that it sounds like this: “A young cell is born on an empty cell if it has exactly three neighbors, among which there are at least two old cells.” I’ll try to explain why the birth rule caused such an effect.
In the game Life there is such a thing as the speed of light. This is the ultimate speed with which an infinite or closed row of cells can move and it is equal to one cell per generation. In Steppers, a row of young cells cannot spawn a new row; for this, he must first grow old. Therefore, the speed of propagation of an infinite number of cells in Steppers is twice lower than in the game Life and amounts to one cell in two generations.
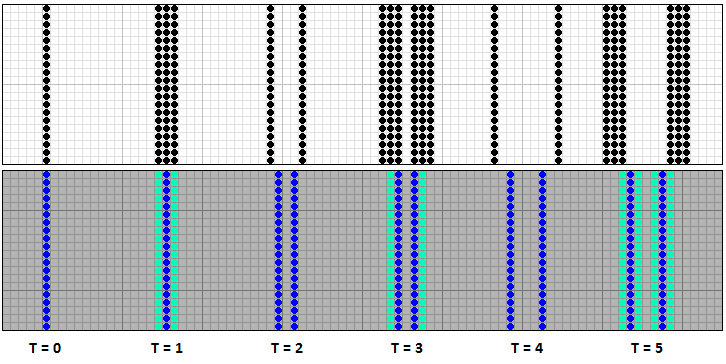
[10] The evolution of an infinite number of cells in the game Life and Steppers
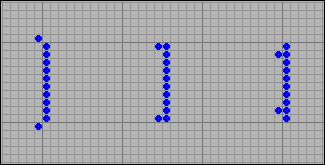
Now consider the evolution of a finite series of cells. In the Life game, opposite the extreme cells, a new cell cannot be born, since it has only two neighbors, so each subsequent generation of the new row becomes two cells shorter, and after a while fades. The same picture is observed during the evolution of a number of cells in the Steppers CA, only twice as slow.

[11] Evolution of a finite row of cells in the game Life and Steppers
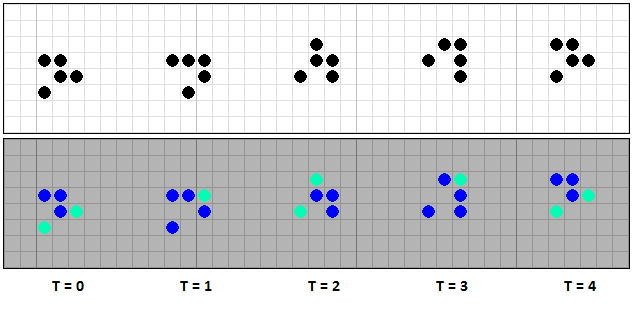
But if in Steppers on one side of the row one neighbor is added to the extreme cells so that it does not die out in the first generation, the picture changes completely. You can add neighbors in one of the following ways.
[12] Transformation of a number of cells into a stepper
In this case, at the aging stage, one cell is born along the edges of the row, and its width is restored. Two old and one young cells can already spawn a new cell and, thus, a series of cells continues to move, continuously restoring its width.
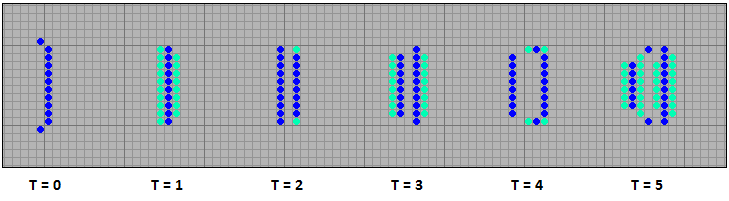
[13] Restoring the width of a number of cells
Using this technique, you can create a stepper of any size. Below is a row of 100 cells and a graceful stepper that came out of it after several hundred generations. Its period is eight.
[14] 100-cell stepper
Steppers can be adjacent or composite, they can closely interact or even move as a whole. Here is a small example of various steppers.

[15] Examples of steppers
The sizes of steppers can be infinitely large, not only in width, but also in length. As shown forum member Conway's Game of Life Emerson J. Perkins ( your Emerson J. Perkins (knightlife) ), using regular items in any order can be constructed stepper arbitrary length.
[16] Designing an arbitrary length stepper
Unfortunately, other types of moving configurations are not known at this time except gliders and steppers. But I still hope that they exist. The steppers shown above do not leave any configurations behind them, that is, they are spaceships. Other steppers in the process of moving can leave various stationary configurations, emit gliders and steppers, and often they are simply followed by unremitting chaos.
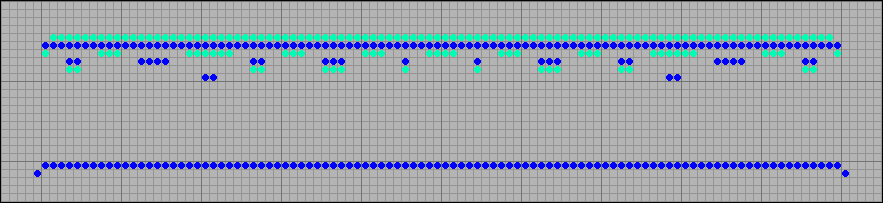
In accordance with the terminology of the game Life, moving configurations that leave trash behind themselves are called puffers . In the following figure, you can see a selection of steam locomotives that, when moving, leave behind a chain of stationary configurations. A steam locomotive generating a chain of two blocks has a record-breaking short period, p 6. At a speed of movement c / 2 , the blocks are stacked with a period of only three cells. Closer is simply impossible. The last engine forms a continuous line. This allows it to be classified as a wickstretcher extension .
[17] Steam
locomotives Steam locomotives generating moving configurations are called rakes ( rake) Such an unexpected name is the result of an inaccurate translation. According to Müller's dictionary, the word rake has many meanings, including the naval “longitudinal fire . " I suspect that this is what the authors of the term rake meant . But a rake has taken root in us, we’ll have to put up with it. Depending on the direction of fire, the rake is divided into front, side and reverse. In Steppers, rakes are fired by gliders and steppers. Below you can see various options for rake-shooters.
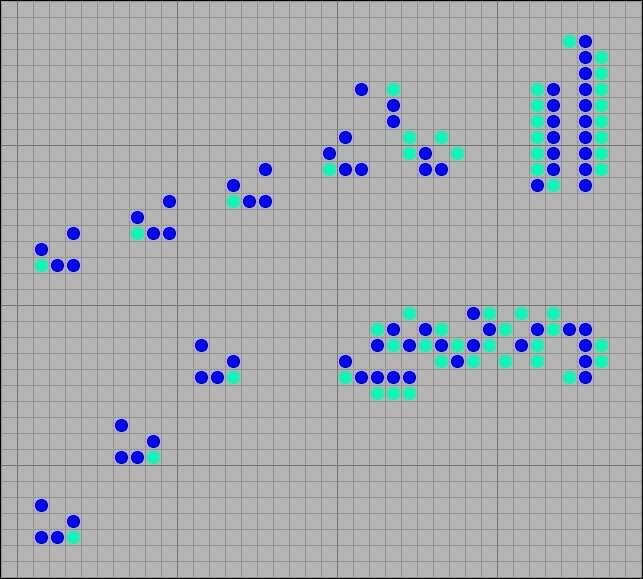
[18] Rake firing gliders, front and back
[19] Side rake

[20] Reverse rake
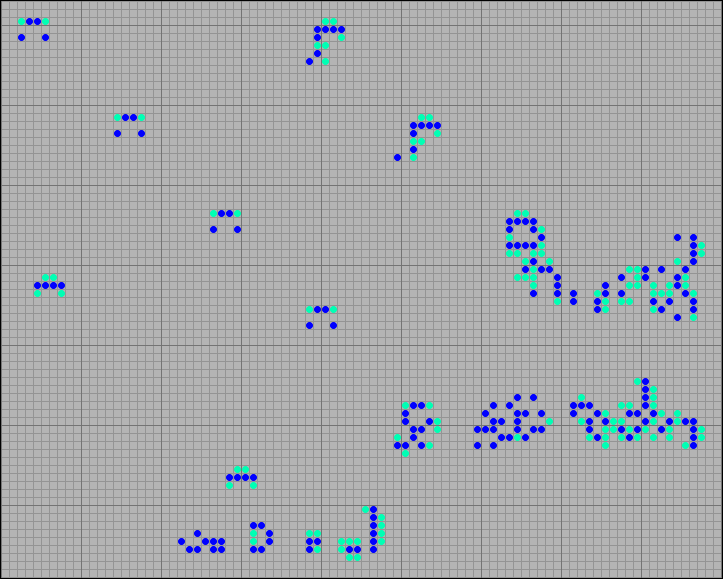
Not all locomotives have such a narrow specialization. Locomotives in the following figure, along with stationary configurations, produce reverse steppers.
[21] Inverse rake plus stationary configurations
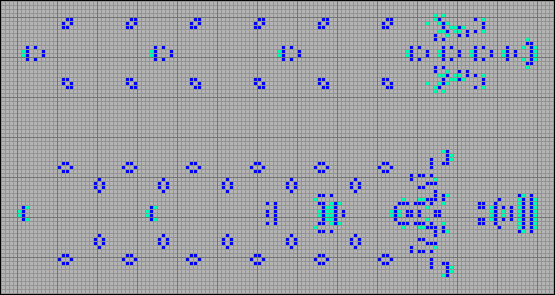
And this engine leaves behind itself in one period two barges, two boats, four side steppers and four reverse, including one large stepper 12 cells wide.
[22] Reverse, side rake plus stationary configurations
Unfortunately, no steam locomotives have been found, leaving behind oscillators, periodic configurations. In fact, there is a steam engine generating a pair of beacons, but they are difficult to notice against the background of other garbage. So this is, rather, an exception to the rule.
Breeder (breeders) This configuration provides the quadratic growth of the population. The essence of quadratic growth is that the multiplier generates configurations, which, in turn, also generate some configurations. There are two types of breeders in Steppers, this is a rake shooting a rake and a rake shooting a steam locomotive leaving stationary configurations (I hope that this proposal will never be taken out of context).
In the following figure, you can see the multiplier, type MMS (moving-moving-stationary) . This means that a moving object produces a moving one that generates stationary objects. With a period of p240, he produces four steam locomotives that form a chain of tubs.
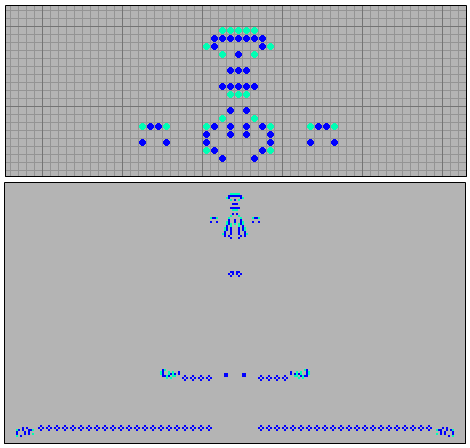
[23] MMS type multiplier
The following breeder is of type MMM (moving-moving-moving) . With a period of p32 he releases a rake shooting simple steppers. It should be noted the small size of this multiplier, only 15 cells bounded by a rectangle of 5 × 9 cells. In the game Life, the smallest configuration having quadratic growth is “26-cell quadratic growth” , its size, as the name implies, is 26 cells, and its size is 16193 × 15089 cells.
[24] Type MMM breeder
Emerson J. Perkins discoveredvery interesting breeder. In his opinion, this does not occur in other well-known cellular automata. When two identical transverse rakes interact, the same rake is generated. That is, two configurations directly give rise to their own kind.

[25] Two identical configurations give rise to their own kind.
Emerson J. Perkins constructed several more “synthetic” propagators. Below are the multipliers MMS and MMM type. During their creation, elements of glider synthesis were used, which allows us to hope for its possibility.
[26] MMS Perkins multiplier

[27] MMM Perkins multiplier
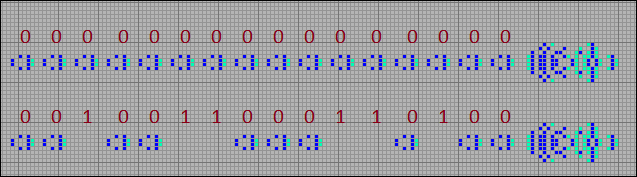
There are configurations that release reverse rakes in the opposite direction. These configurations are not destined to become multipliers, since the stream of steppers from the first issued reverse rake destroys all subsequent ones. Despite this, such patterns are of some interest. The fact is that in collisions of a newly released reverse rake with a stream of steppers from the first reverse rake, an unexpected effect is manifested. Each issued reverse rake destroys the first stepper in the stream, but at the same time restores all previously destroyed ones. But that is how the binary counter works. If we consider the chain of steppers as a sequence of bits and, at the same time, take the missing stepper as “1”, and the present as “0”, you can see how the issued reverse rake is counted

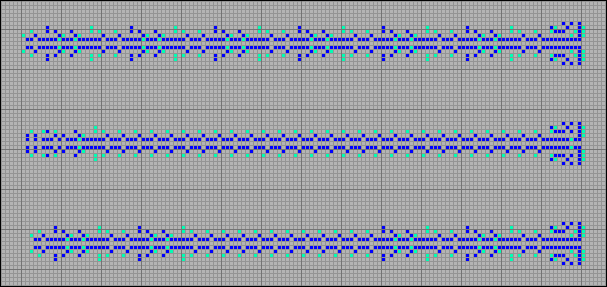
[28] Counter
Let's try to create a counter based on this pattern and check how it works. We restrict ourselves to 16 digits, that is, leave 16 steppers in the stream. Take an arbitrary number, for example, 9780. Its binary representation is 0010011000110100. Given that the period of our counter is p48 , the specified number of back rakes will be released in 9780 * 48 = 469440 generation. Now compare the state of the counter in 0 and 469440 generation. You can verify that the counter is working. The sequence of steppers contains the number we set.
[29] Example of operation of the counter
The gun (Gun) is called a motionless configuration releasing gliders or spaceships. At the moment, three rifles are known that shoot steppers; glider rifles have not yet been found. The first of these guns produces four steppers with a width of four cells. Its period is p32 . The figure shows the sequence of generations T = 0, 6, 12, 18, 24, 32.

[30] A shotgun that shoots steppers with a width of 4 cells in four directions
The second gun has a period of p14 and produces four steppers with a width of five cells. The figure shows the sequence of generations T = 0, 3, 6, 9, 12, 14.

[31] A shotgun that shoots steppers with a width of 5 cells in four directions
And finally, a gun, which, as expected, shoots in one direction. Its period is p10 and it produces steppers six cells wide.

[32] A 6-cell wide shotgun
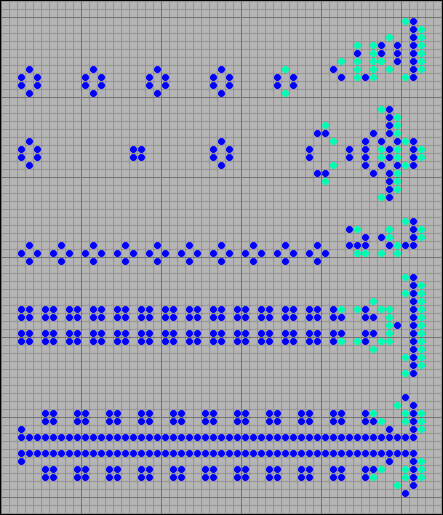
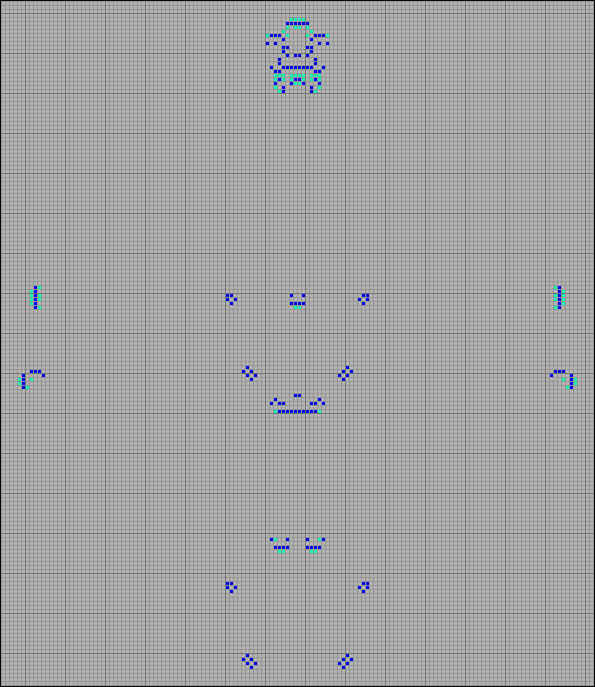
Oscillators are fixed configurations that are predecessors of themselves. In their development, after several generations they return to some initial state. At present, about 200 oscillators are known. Some of them have doubles from the game Life. It is seen that due to the aging of cells, their period changes upwards. However, not all. The boiler (the Cauldron) , an oscillator in the last row, in the game of life is a period p8 . At Steppers, his period was reduced to p5 .
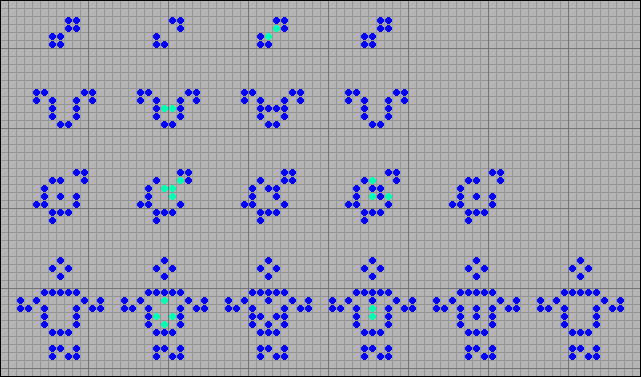
[33] Changing the periods of oscillators from the Life game
As an experiment, a large group of oscillators from the Life game was transferred to the Steppers cellular automaton. Some of them survived, that is, they remained oscillators. Below, a part of them is shown.

[34] Oscillators existing in the game Life.
To search for oscillators in Steppers, a special program was created with a rather primitive algorithm. In the center of the toroidal lattice with a size of 256x256 cells, an area of 16 x 16 was filled with cells with a random state. 12 types of symmetry of the contents of the square were randomly selected. Then, for 500 generations, the contents of the central region were compared with 32 previous states. If more than a period ago, the current state has already met, its contents are displayed in a text file. Once deduced patterns were not repeatedly presented. Then, from a rather voluminous text file, manually managed to select quite interesting oscillators. Here are some examples of them.

[35] Examples of oscillators found in Steppers
And here is an almost complete collection of currently known oscillators

[36] Steppers cellular automaton oscillators
There are a lot of collision options in Steppers, this is due to the wide variety of steppers. Because of this, it’s hard to get at least a complete overview of collisions, even for simple steppers. However, experiments have shown that in collisions, gliders and steppers can be destroyed, born, and change direction. Due to the increased survivability of the Steppers cellular automaton, often the result of collisions is an uncontrollable population growth. Probably, this can become an obstacle for the problems of glider synthesis and synthesis with the participation of steppers.
And now a few examples. Below are shown options for the collision of the glider with the block. As can be seen, the result of the collision may be stepper, hive (beehive) and a ship (ship). Conversely, a glider may collide with a hive as a result of a block.

[37] Examples of collisions between a glider and a block.
The following illustration shows examples of collisions of two simple steppers. In a head-on collision, a pond remains, and in a side-by-side oscillator, a buoy.
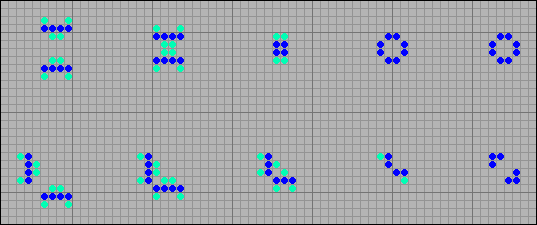
[38] Examples of the collision of two steppers
Member Forum Conway, NH's the Game of Life Juho Pystynen (Tropylium) offered an interesting and functional examples of collisions. With his permission, I publish some of them.
In the first example, four steppers flow from diverging inverse rakes. In an off-center collision, they annihilate, emitting four streams of gliders.

[39] Four streams of steppers give rise to gliders
In the following example, seven gliders are reflected from two parallel streams of steppers generated by the corresponding inverse rake. When gliders collide with a stepper stream, a sequence of blocks is formed.
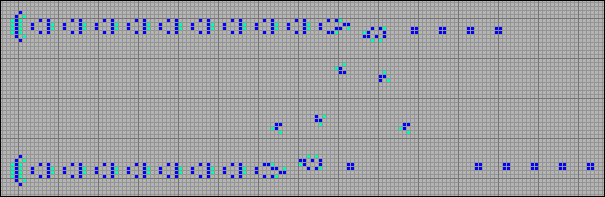
[40] Reflection of the gliders
The article presents the results of a rather superficial study of the Steppers cellular automaton. Many questions remain unresolved. For instance:
I hope that these open-ended questions will attract amateurs to the study of the Steppers cellular automaton. I am sure that at the moment it is incomparably easier to make any discovery in Steppers than, in the length and breadth of the studied game Life.
MilhinSA.Golly2.5.zip (48.2 kb) - MilhinSA rule and example rle-files.
Steppers-catalog.zip (221 kb) - Catalog of configurations of the cellular machine Steppers.
SidorovI.Golly2.5.zip (18.9 kb) - SidorovI rule with examples.
SidorovI.Science_and_Life_1975.03.djvu (187 kb) - Article by I. Sidorov in the journal "Science and Life", 1975.03.
For stable configurations, the new rules coincide with the rules of the Life game, therefore, all stable configurations in the Life game exist in the new rules. In the described cellular automaton there is a large class of moving configurations, spaceships. All these configurations move along the same progressive mechanism, which resembles the movement of a stepper excavator and a person on crutches. I called such spaceships a stepper , and the Steppers rule itself. So we will call it in the future.
There are quite a few oscillators in Steppers, and some oscillators from the game Life work in Steppers, which indicates the continuity of the rules. And finally, the famous Conway glider also exists in the proposed rules. The article will consider the dynamics of randomly filled gratings, reveal the mechanism of movement of the steppers, describe the currently found oscillators and steppers. Examples of collisions and complex functional behavior will also be given.

[00] An example of a moving configuration generating a stream of steppers
Rules Development History
In 1988, I worked in a laboratory for technical vision. Studying the algorithm of skeletonization of a raster monochrome image, I wrote a program for its implementation. The skeletonization algorithm itself was never useful to us and was abandoned, and the program we wrote turned out to be a pretty decent cellular automaton with a graphical editor and graphical output after a little refinement. The first test for her, of course, was the game Life of John Conway. After a while, I wanted to experiment with other rules, and I remembered the article I read earlier, " Evolution of the game Evolution"in the journal" Science and Life "for 1975 [1]. In this article, trying to develop the game Life, the author I. Sidorov added a third state for newly born cells. Under the new rules, a cell can be in three states, empty, young and old. A young cell does not die under any circumstances, and in the next generation becomes old.

[01] Designation of cell conditions
I. Sidorov formulated all the rules completely in the following form:
- A young cell in one move does not die of either overpopulation or loneliness. After one move, the young cell turns into the old one.
- In each empty cell, a new (young) cell is born if this cell had three neighbors (both old and young cells could be neighbors).
- An old cell dies from overpopulation if it borders on four (or more) old cells or if it borders on three (or more) cells, among which there is at least one young one.
- An old cell dies of loneliness if it is isolated or has only one neighbor (both an old and a young cell can be a neighbor).
There are two ships described by him in I. Sidorov’s cellular automaton. Later I managed to find two oscillators. Unfortunately, when a certain critical mass is exceeded, the population loses its structure and grows rapidly. Since it was not interesting to observe this, I undertook to develop my own laws of life and death.
After selecting various options, the following rules were formed:
- A young cell in one move does not die of either overpopulation or loneliness. After one move, the young cell turns into the old one (this rule is left unchanged).
- A young cell is born on an empty cell if it has exactly three neighbors, among which there are at least two old cells.
- The old cell continues to exist in the next generation if it has two or three neighboring cells, among which no more than one is young.
More clearly, the rules can be presented in the form of tables. The axes show the number of young and old neighbors.

[02] Tabular presentation of the rule I. Sidorov

[03] Tabular presentation of the rule Steppers
This rule seemed so interesting to me that I wrote my article and sent it to the same journal, Science and Life. After some time, I received an answer that in the near future publications on cellular automata are not planned. For more than twenty years, I slowly, with large interruptions, worked on this cellular automaton, but made no attempt to publish it anywhere. And only with the advent of the wonderful Golly program, in which you can create cellular automata according to arbitrary rules, did the opportunity to share your modest research appear. Golly is free and can be downloaded from http://sourceforge.net/projects/golly/ .
All illustrations in this article are indexed, if desired, you can download the MilhinSA.Golly2.5.zip archivein which rle-files with all examples are located under the corresponding index. In this case, you can not be content with static pictures, but see the process in action. Golly can open this archive with the rule and examples without first unpacking it.
In March 2012, I posted a post about Steppers cellular machine at the Conway's Game of Life English forum . The message aroused some interest among the forum participants, some of them took part in the Steppers study and shared their findings.
Dynamics
The best way to check the integral characteristics of a cellular automaton is to send a noise signal, or, in other words, a randomly populated population to its input. The following figure shows the evolution of a randomly filled toroidal grid of the game Life and Steppers in generations 32, 320, and 3200. It can be seen that the population density of Steppers decreases more slowly than in the game Life and stabilizes at some stage.

[04] Evolution of a random population of the game Life and Steppers
To obtain statistically reliable data, the following computational experiment was conducted. For each rule, a randomly filled toroidal field of 256 x 256 cells with a density of 50% was formed. The cellular machine worked out up to 10,000 generations. For each generation, the field density was calculated as a percentage, as well as the percentage of cells that changed their state. The last parameter characterizes the activity of the cellular automaton. For each machine, this process was repeated 1000 times, then the output was averaged.
Below are graphs of density and activity. From these graphs it can be seen that the density and, accordingly, the activity of the game Life quickly drops at the very beginning of development and in the 3000-4000 generation decreases on average to 3% of the density. Activity drops to an average of 1%. It is easy to understand that these are the remaining stationary configurations and simple oscillators. The cellular machine Steppers evolves in a different scenario. For about 20 generations, a balance has been established between young and old cells, which leads to a damped oscillatory process. Then the density begins to decrease, and in the 500-700 generation it stabilizes by 21%. Activity stabilizes by 14%. Thus, the evolution of a random field of sufficient size continues indefinitely.

[05] Graphs of changes in density and activity
Graphs of changes in density and activity show the average value for the entire field, but the density and activity of cells changes not only in time but also in space. During the evolution of a uniformly filled random field, it can be seen that the cells are grouped into active regions, forming some texture. To highlight areas with increased activity, a special cellular automaton mapping algorithm was applied. It works as follows. For each cell over 32 generations, the number of births and deaths is calculated. Then the image of the cellular automaton in the black-red-yellow-white palette is displayed. The following figure shows that the active cells in the game Life quite quickly break up into isolated areas, which subsequently die out. In the Steppers cellular machine, the active areas are constantly changing shape and size, merge and disintegrate. Sufficiently large areas remain free and there are hospitals, oscillators, as well as gliders and steppers. Due to this, even with the evolution of a random field, a rather interesting picture arises as a result of self-organization, which is interesting to observe.

[06] Change in population activity during evolution
It should be recognized that the Stepper rule is not only very tenacious, but also very explosive. Often, the interaction of simple configurations leads to uncontrollable population growth. On the Conway's Game of Life forum , minimum size configurations were found that caused unlimited population growth. The following figure depicts a 5-cell pattern, as well as its state in the 1500 generation, and not completely. The population size is slightly less than 20,000 cells.

[07] The 5-cell pattern in the 1500th generation The
linear 7-cell pattern is developing even more intensively. Here he is depicted in the 500th generation, the population size of 8 124 cells. In the 3000 generation, the population size will exceed 500,000 cells.

[08] 7-cell pattern in the 500th generation
Movement, steppers
In the Steppers cellular automaton, at the moment, two types of moving configurations are found. Moreover, the only type refers to the first type, which is called the glider in the game Life. It is seen that the glider in Steppers is very slightly different from the glider from the game Life. With such a significant difference between these rules, the existence of gliders was rather unexpected.

[09] Comparison of the gliders of the game Life and Steppers
The steppers belong to another type, and their number is unlimited, since their size is unlimited. All steppers are united in the same way of movement. And this method owes its existence to the birth rule. Let me remind you that it sounds like this: “A young cell is born on an empty cell if it has exactly three neighbors, among which there are at least two old cells.” I’ll try to explain why the birth rule caused such an effect.
In the game Life there is such a thing as the speed of light. This is the ultimate speed with which an infinite or closed row of cells can move and it is equal to one cell per generation. In Steppers, a row of young cells cannot spawn a new row; for this, he must first grow old. Therefore, the speed of propagation of an infinite number of cells in Steppers is twice lower than in the game Life and amounts to one cell in two generations.

[10] The evolution of an infinite number of cells in the game Life and Steppers
Now consider the evolution of a finite series of cells. In the Life game, opposite the extreme cells, a new cell cannot be born, since it has only two neighbors, so each subsequent generation of the new row becomes two cells shorter, and after a while fades. The same picture is observed during the evolution of a number of cells in the Steppers CA, only twice as slow.

[11] Evolution of a finite row of cells in the game Life and Steppers
But if in Steppers on one side of the row one neighbor is added to the extreme cells so that it does not die out in the first generation, the picture changes completely. You can add neighbors in one of the following ways.

[12] Transformation of a number of cells into a stepper
In this case, at the aging stage, one cell is born along the edges of the row, and its width is restored. Two old and one young cells can already spawn a new cell and, thus, a series of cells continues to move, continuously restoring its width.

[13] Restoring the width of a number of cells
Using this technique, you can create a stepper of any size. Below is a row of 100 cells and a graceful stepper that came out of it after several hundred generations. Its period is eight.

[14] 100-cell stepper
Steppers can be adjacent or composite, they can closely interact or even move as a whole. Here is a small example of various steppers.

[15] Examples of steppers
The sizes of steppers can be infinitely large, not only in width, but also in length. As shown forum member Conway's Game of Life Emerson J. Perkins ( your Emerson J. Perkins (knightlife) ), using regular items in any order can be constructed stepper arbitrary length.

[16] Designing an arbitrary length stepper
Unfortunately, other types of moving configurations are not known at this time except gliders and steppers. But I still hope that they exist. The steppers shown above do not leave any configurations behind them, that is, they are spaceships. Other steppers in the process of moving can leave various stationary configurations, emit gliders and steppers, and often they are simply followed by unremitting chaos.
Steam locomotives and rakes
In accordance with the terminology of the game Life, moving configurations that leave trash behind themselves are called puffers . In the following figure, you can see a selection of steam locomotives that, when moving, leave behind a chain of stationary configurations. A steam locomotive generating a chain of two blocks has a record-breaking short period, p 6. At a speed of movement c / 2 , the blocks are stacked with a period of only three cells. Closer is simply impossible. The last engine forms a continuous line. This allows it to be classified as a wickstretcher extension .

[17] Steam
locomotives Steam locomotives generating moving configurations are called rakes ( rake) Such an unexpected name is the result of an inaccurate translation. According to Müller's dictionary, the word rake has many meanings, including the naval “longitudinal fire . " I suspect that this is what the authors of the term rake meant . But a rake has taken root in us, we’ll have to put up with it. Depending on the direction of fire, the rake is divided into front, side and reverse. In Steppers, rakes are fired by gliders and steppers. Below you can see various options for rake-shooters.

[18] Rake firing gliders, front and back

[19] Side rake

[20] Reverse rake
Not all locomotives have such a narrow specialization. Locomotives in the following figure, along with stationary configurations, produce reverse steppers.

[21] Inverse rake plus stationary configurations
And this engine leaves behind itself in one period two barges, two boats, four side steppers and four reverse, including one large stepper 12 cells wide.

[22] Reverse, side rake plus stationary configurations
Unfortunately, no steam locomotives have been found, leaving behind oscillators, periodic configurations. In fact, there is a steam engine generating a pair of beacons, but they are difficult to notice against the background of other garbage. So this is, rather, an exception to the rule.
Multipliers
Breeder (breeders) This configuration provides the quadratic growth of the population. The essence of quadratic growth is that the multiplier generates configurations, which, in turn, also generate some configurations. There are two types of breeders in Steppers, this is a rake shooting a rake and a rake shooting a steam locomotive leaving stationary configurations (I hope that this proposal will never be taken out of context).
In the following figure, you can see the multiplier, type MMS (moving-moving-stationary) . This means that a moving object produces a moving one that generates stationary objects. With a period of p240, he produces four steam locomotives that form a chain of tubs.

[23] MMS type multiplier
The following breeder is of type MMM (moving-moving-moving) . With a period of p32 he releases a rake shooting simple steppers. It should be noted the small size of this multiplier, only 15 cells bounded by a rectangle of 5 × 9 cells. In the game Life, the smallest configuration having quadratic growth is “26-cell quadratic growth” , its size, as the name implies, is 26 cells, and its size is 16193 × 15089 cells.

[24] Type MMM breeder
Emerson J. Perkins discoveredvery interesting breeder. In his opinion, this does not occur in other well-known cellular automata. When two identical transverse rakes interact, the same rake is generated. That is, two configurations directly give rise to their own kind.

[25] Two identical configurations give rise to their own kind.
Emerson J. Perkins constructed several more “synthetic” propagators. Below are the multipliers MMS and MMM type. During their creation, elements of glider synthesis were used, which allows us to hope for its possibility.

[26] MMS Perkins multiplier

[27] MMM Perkins multiplier
Counters
There are configurations that release reverse rakes in the opposite direction. These configurations are not destined to become multipliers, since the stream of steppers from the first issued reverse rake destroys all subsequent ones. Despite this, such patterns are of some interest. The fact is that in collisions of a newly released reverse rake with a stream of steppers from the first reverse rake, an unexpected effect is manifested. Each issued reverse rake destroys the first stepper in the stream, but at the same time restores all previously destroyed ones. But that is how the binary counter works. If we consider the chain of steppers as a sequence of bits and, at the same time, take the missing stepper as “1”, and the present as “0”, you can see how the issued reverse rake is counted

[28] Counter
Let's try to create a counter based on this pattern and check how it works. We restrict ourselves to 16 digits, that is, leave 16 steppers in the stream. Take an arbitrary number, for example, 9780. Its binary representation is 0010011000110100. Given that the period of our counter is p48 , the specified number of back rakes will be released in 9780 * 48 = 469440 generation. Now compare the state of the counter in 0 and 469440 generation. You can verify that the counter is working. The sequence of steppers contains the number we set.

[29] Example of operation of the counter
Shotguns
The gun (Gun) is called a motionless configuration releasing gliders or spaceships. At the moment, three rifles are known that shoot steppers; glider rifles have not yet been found. The first of these guns produces four steppers with a width of four cells. Its period is p32 . The figure shows the sequence of generations T = 0, 6, 12, 18, 24, 32.

[30] A shotgun that shoots steppers with a width of 4 cells in four directions
The second gun has a period of p14 and produces four steppers with a width of five cells. The figure shows the sequence of generations T = 0, 3, 6, 9, 12, 14.

[31] A shotgun that shoots steppers with a width of 5 cells in four directions
And finally, a gun, which, as expected, shoots in one direction. Its period is p10 and it produces steppers six cells wide.

[32] A 6-cell wide shotgun
Oscillators
Oscillators are fixed configurations that are predecessors of themselves. In their development, after several generations they return to some initial state. At present, about 200 oscillators are known. Some of them have doubles from the game Life. It is seen that due to the aging of cells, their period changes upwards. However, not all. The boiler (the Cauldron) , an oscillator in the last row, in the game of life is a period p8 . At Steppers, his period was reduced to p5 .

[33] Changing the periods of oscillators from the Life game
As an experiment, a large group of oscillators from the Life game was transferred to the Steppers cellular automaton. Some of them survived, that is, they remained oscillators. Below, a part of them is shown.

[34] Oscillators existing in the game Life.
To search for oscillators in Steppers, a special program was created with a rather primitive algorithm. In the center of the toroidal lattice with a size of 256x256 cells, an area of 16 x 16 was filled with cells with a random state. 12 types of symmetry of the contents of the square were randomly selected. Then, for 500 generations, the contents of the central region were compared with 32 previous states. If more than a period ago, the current state has already met, its contents are displayed in a text file. Once deduced patterns were not repeatedly presented. Then, from a rather voluminous text file, manually managed to select quite interesting oscillators. Here are some examples of them.

[35] Examples of oscillators found in Steppers
And here is an almost complete collection of currently known oscillators

[36] Steppers cellular automaton oscillators
Clashes
There are a lot of collision options in Steppers, this is due to the wide variety of steppers. Because of this, it’s hard to get at least a complete overview of collisions, even for simple steppers. However, experiments have shown that in collisions, gliders and steppers can be destroyed, born, and change direction. Due to the increased survivability of the Steppers cellular automaton, often the result of collisions is an uncontrollable population growth. Probably, this can become an obstacle for the problems of glider synthesis and synthesis with the participation of steppers.
And now a few examples. Below are shown options for the collision of the glider with the block. As can be seen, the result of the collision may be stepper, hive (beehive) and a ship (ship). Conversely, a glider may collide with a hive as a result of a block.

[37] Examples of collisions between a glider and a block.
The following illustration shows examples of collisions of two simple steppers. In a head-on collision, a pond remains, and in a side-by-side oscillator, a buoy.

[38] Examples of the collision of two steppers
Member Forum Conway, NH's the Game of Life Juho Pystynen (Tropylium) offered an interesting and functional examples of collisions. With his permission, I publish some of them.
In the first example, four steppers flow from diverging inverse rakes. In an off-center collision, they annihilate, emitting four streams of gliders.

[39] Four streams of steppers give rise to gliders
In the following example, seven gliders are reflected from two parallel streams of steppers generated by the corresponding inverse rake. When gliders collide with a stepper stream, a sequence of blocks is formed.

[40] Reflection of the gliders
Conclusion
The article presents the results of a rather superficial study of the Steppers cellular automaton. Many questions remain unresolved. For instance:
- It is not known whether glider guns exist.
- Not a single spaceship has been discovered that would not be a stepper or glider, although there is no reason to think that they are impossible.
- No steam locomotives left behind oscillators
- No agar has been studied at all. These are configurations covering the entire plane and periodic in space and time.
- No eaters, configurations, absorbing gliders or steppers were found without harming themselves.
- Glider synthesis has not been studied as well as synthesis with the help of steppers.
I hope that these open-ended questions will attract amateurs to the study of the Steppers cellular automaton. I am sure that at the moment it is incomparably easier to make any discovery in Steppers than, in the length and breadth of the studied game Life.
Download Files
MilhinSA.Golly2.5.zip (48.2 kb) - MilhinSA rule and example rle-files.
Steppers-catalog.zip (221 kb) - Catalog of configurations of the cellular machine Steppers.
SidorovI.Golly2.5.zip (18.9 kb) - SidorovI rule with examples.
SidorovI.Science_and_Life_1975.03.djvu (187 kb) - Article by I. Sidorov in the journal "Science and Life", 1975.03.
