How to deal with reposts or a few words about perceptual hashes
This publication will discuss approaches to constructing perceptual image hashes and the possibilities for using them (for example, duplicate searches).
perceptual hash algorithms describe a class of functions for generating comparable hashes. They use various image properties to build an individual “imprint”. In the future, these "prints" can be compared with each other.
If the hashes are different, then the data is different. If the hashes match, then the data is most likely the same (since there is a chance of collisions, then the same hashes do not guarantee that the data matches). This article will discuss several popular methods for constructing perceptual image hashes, as well as a simple way to deal with collisions. Anyone who is interested, please, under the cat.
There are many different approaches to creating a perceptual image hash. All of them are united by 3 main stages:
In this publication, we will not concern the implementation of the above algorithms. It is an overview and talks about different approaches to building hashes.
We will look at 4 different hash algorithms: Simple Hash [4], DCT Based Hash [1], [11], Radial Variance Based Hash [1], [5] and Marr- Hildreth Operator Based Hash [1], [6] .
The essence of this algorithm is to display the average value of low frequencies. In images, high frequencies provide detail, while low frequencies show structure. Therefore, to build such a hash function, which for similar images will produce a close hash, you need to get rid of high frequencies. Principle of operation:
The resulting hash is resistant to scaling, compressing or stretching the image, changing the brightness, contrast, color manipulation. But the main advantage of the algorithm is its speed. To compare hashes of this type, the normalized Hamming distance function is used.

Original Image

Received “Fingerprint”
The discrete cosine transform (DCT) [7] is one of the orthogonal transforms that is closely related to the discrete Fourier transform (DFT) and is a homomorphism of its vector space. DCT, like any Fourier-oriented transformation, expresses a function or signal (a sequence of a finite number of data points) as a sum of sinusoids with different frequencies and amplitudes. DCT uses only cosine functions, unlike DFT, which uses both cosine and sine functions. There are 8 types of DCT [7]. The most common is the second type. We will use it to build a hash function.
Let's see what the second type of DCT is:
Let x [m], where m = 0, ..., N - 1 is a sequence of signal lengths N. Define the second type of DCT, as
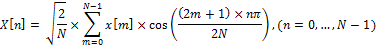
This expression can be rewritten as:
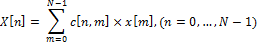
where c [n, m] is an element of the DCT matrix at the intersection of a row with number n and a column with number m.
DCT matrix is defined as:
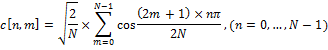
This matrix is very convenient for calculating DCT. DCT can be calculated in advance, for any required length. Thus, DCT can be represented in the form:
DCT = M × I × M '
Where M is the DCT matrix, I is the square-sized image, M' is the inverse matrix.
Low-frequency DCT coefficients are most stable to image manipulation. This is because most of the signal information is usually concentrated in several low-frequency coefficients. As a matrix I, an image is usually taken, compressed to a size of 32x32 and simplified using various filters, for example, bleaching. The result is a DCT matrix (I), in the upper left corner of which there are low-frequency coefficients. To build a hash, the upper left 8x8 frequency block is taken. Then, a 8-byte hash is built from this block by finding the middle and constructing a chain of bits (just like in Simple Based Hash).
We list the steps for constructing a hash using this algorithm:
The main advantages of such a hash are resistance to small turns, blurring and compression of the image, as well as the speed of comparing hashes due to their small size. To compare hashes of this type, the Hamming distance function is used.
The idea of the Radial Variance Based Hash algorithm is to construct a ray dispersion vector (LDP) based on the Radon transform [5]. Then DCT is applied to the DVD and the hash is calculated. The Radon transform is an integral transform of the function of many variables along a straight line. It is resistant to image processing using various manipulations (e.g., compression) and geometric transformations (e.g., rotations). In the two-dimensional case, the Radon transform for the function f (x, y) looks like this:
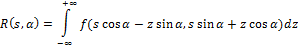
The Radon transform has a simple geometric meaning - it is the integral of the function along a straight line perpendicular to the vector n = (cos a, sin a) and passing at a distance s (measured along the vector n, with the corresponding sign) from the origin.
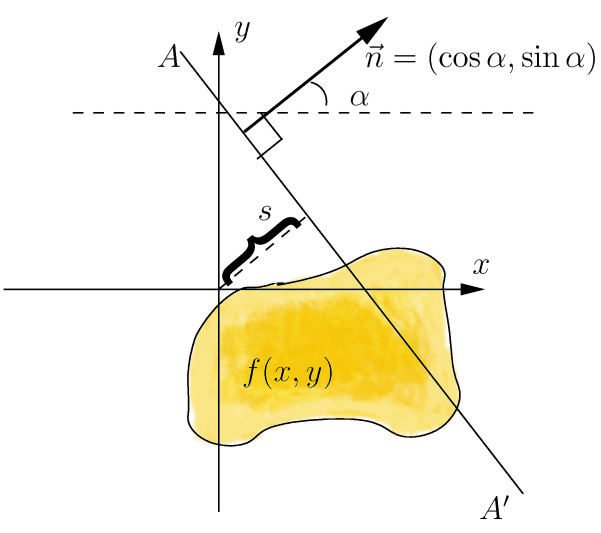
To expand the Radon transform for discrete images, the linear integral along the straight line d = x ∙ cos α + y ∙ sin α can be approximated by summing the values of all pixels lying in a line with a width of one pixel:
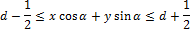
Later it was found that it is better to use the variance instead of the sum of the values pixels along the projection line [6]. Dispersion handles luminance gaps along the projection line much better. Such luminance gaps appear due to edges that are orthogonal to the projection line.
Now we define the ray vector of dispersion. Let Γ (α) be the set of pixels on the projection line corresponding to a given angle. Let (x ′, y ′) be the coordinates of the central pixel in the image. x, y belong to Γ (α) if and only if

Now we define the radial variance vector:
Let I (x, y) denote the brightness of the pixel (x, y), # Г (α) is the cardinality of the set, then the ray dispersion vector R [α], where α = 0,1, ..., 179 we define as
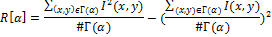
It is enough to construct the vector from 180 values of the angle, since the Radon transform is symmetric. The resulting vector can be used to construct a hash, but this algorithm proposes some more improvement - apply DCT to the resulting vector. The result is a vector that inherits all the important properties of DCT. The first 40 coefficients of the resulting vector, which correspond to low frequencies, are taken as a hash. Thus, the size of the received hash is 40 bytes.
So, we list the steps for constructing a hash using this algorithm:
To compare hashes of this type, a peak search for the cross-correlation function is used.
The Marra-Hildreth operator [16] allows you to define the edges in the image. Generally speaking, a border in an image can be defined as an edge or contour separating adjacent portions of an image that have relatively excellent characteristics in accordance with certain features. These features can be color or texture, but most often the gray gradation of the image color (brightness) is used. The result of determining the boundaries is a border map. A border map describes the classification of borders for each pixel in an image. If the boundaries are defined as a sharp change in brightness, then derivatives or a gradient can be used to find them.
Let the function indicates the brightness level for the line (one-dimensional array of pixels). The first approach to determining the boundaries is to find local extrema of the function, that is, the first derivatives. The second approach (Laplace's method) is to find the second derivatives
indicates the brightness level for the line (one-dimensional array of pixels). The first approach to determining the boundaries is to find local extrema of the function, that is, the first derivatives. The second approach (Laplace's method) is to find the second derivatives  [1].
[1].
Both approaches can be adapted for the case of two-dimensional discrete images, but with some problems. To find the derivatives in the discrete case, approximation is required. In addition, noise in the image can significantly degrade the process of finding boundaries. Therefore, before determining the boundaries to the image, you need to apply some kind of filter that suppresses noise. To build a hash, you can choose an algorithm that uses the Laplace operator (approach 2) and a Gaussian filter.
We define a continuous Laplacian (Laplace operator):
Let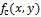 determines the brightness in the image. Then the continuous Laplacian is defined as:
determines the brightness in the image. Then the continuous Laplacian is defined as:
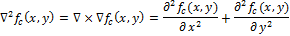
Zero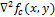 and there are points corresponding to the boundary of the function
and there are points corresponding to the boundary of the function 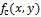 , since these are points at which the second derivative vanishes. Various filters (discrete Laplace operators) can be obtained from continuous Laplacian. Such a filter
, since these are points at which the second derivative vanishes. Various filters (discrete Laplace operators) can be obtained from continuous Laplacian. Such a filter 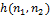 can be applied to a discrete image using the convolution of functions. The Laplace operator for an image
can be applied to a discrete image using the convolution of functions. The Laplace operator for an image 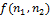 can be rewritten as:
can be rewritten as:
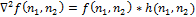
where * denotes a convolution of functions. To construct a map of boundaries, you need to find the zeros of the discrete operator .
.
Now consider the Marra-Hildreth operator. It is also called the Laplacian from the Gauss filter (LoG) - this is a special type of discrete Laplace operator. LoG is constructed by applying the Laplace operator to a Gaussian filter (function). The peculiarity of this operator is that it can highlight borders on a certain scale. The scale variable can be varied in order to better identify the boundaries.
We define the Gaussian filter as:
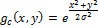
Convolution with the Laplace operation can be interchanged, because the derivative and convolution are linear operators:
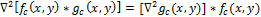
This property allows you to pre-calculate the operator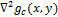 , because it does not depend on the image (
, because it does not depend on the image ( 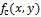 ).
).
(Marra-Hildreth operator, Laplacian from the Gauss filter, LoG). LoG hc (x, y) is defined as:
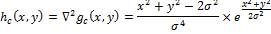
To use LoG in discrete form, we will discretize this equation by substituting the desired scale variable. By default, its value is taken as 1.0. Then the filter can be applied to the image using discrete convolution.
Define a discrete convolution:
Let x, y, z be the pixel width, length, and depth of the image I.
The result R of the convolution of the image I with the mask M is defined as:
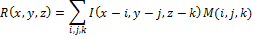
Now, we list the steps of the algorithm that uses the Marr-Hildreth operator to construct the hash:
The size of the received hash is not small, however, comparing the two hashes takes quite a bit of time compared to the Radial algorithm, since the normalized Hamming distance function is used. Also, such an algorithm is sensitive to image rotations, but is resistant to scaling, darkening, and compression.
The Hamming distance determines the number of different positions between two binary sequences.
Definition:
Let A be an alphabet of finite length.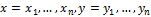 - binary sequences (vectors). We define the Hamming distance Δ between x and y as:
- binary sequences (vectors). We define the Hamming distance Δ between x and y as:
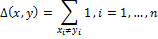
This method of comparing hash values is used in the DCT Based Hash method. The hash is 8 bytes in size, so the Hamming distance lies in the interval [0, 64]. The smaller the Δ value, the more similar the images.
To facilitate comparison, the Hamming distance can be normalized using the length of the vectors: The
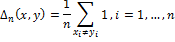
normalized Hamming distance is used in the Simple Hash and Marr-Hildreth Operator Based Hash algorithms. The Hamming distance lies in the interval [0.1] and the closer Δ is to 0, the more similar the images.
The correlation between two signals is defined as:
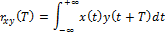
where x (t) and y (t) are two continuous functions of real numbers. The function rxy (t) describes the shift of these two signals relative to time T. The variable T determines how far the signal is shifted to the left. If the signals x (t) and y (t) are different, the function rxy T is called cross-correlation.
We define the Normalized cross-correlation function:
Let xi and yi, where i = 0, ... N - 1 are two sequences of real numbers, and N is the length of both sequences. The delayed armed formations d are defined as:
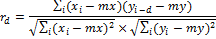
where mx and my denote the average value for the corresponding sequence.
The peak of the cross-correlation function (PCC) is the maximum value of the function rd that can be achieved in the interval d = 0, N.
PCC is used to compare hash values in the Radial Variance Based Hash algorithm. PCC ∈ [0,1], the greater its value, the more similar the images.
We examined 4 different approaches in the implementation of hash algorithms. The scope of perceptual hashes is wide, from searching for similar images to detecting spam in pictures.
In our project, we use a perceptual hash to identify duplicate images. Moreover, it is often possible to successfully compare among themselves images containing watermark'i (obtained from different sources) or images with cropped edges.
The best algorithm for finding duplicates can be considered Radial Variance Based Hash, but it is extremely difficult to use on large amounts of data, due to the very time-consuming comparison of hashes.
For ourselves, we chose DCT based Hash. We use a 64-bit hash, this is enough to find duplicates, however such a small hash size inevitably leads to collisions. We are struggling with collisions by building a histogram (spectrum) for the image.
Each component of the spectrum means the relative number of colors of one or another subrange in the image, in other words, shows the distribution of colors in the image. It looks something like this:
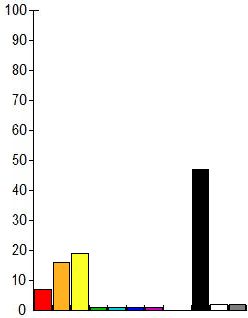
Thus, we first look for images comparing the hash, and then compare the histograms, if the histograms are significantly different, then this image is not considered similar. The histograms themselves can be compared by considering the cross-correlation as well as when comparing the Radial Variance Based Hash, using Pearson cross-correlation:
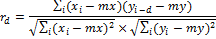
If this topic is of interest to the community, in the next article I will talk specifically about our implementation of DCT hash, as well as how to find the Hamming distance.
perceptual hash algorithms describe a class of functions for generating comparable hashes. They use various image properties to build an individual “imprint”. In the future, these "prints" can be compared with each other.
If the hashes are different, then the data is different. If the hashes match, then the data is most likely the same (since there is a chance of collisions, then the same hashes do not guarantee that the data matches). This article will discuss several popular methods for constructing perceptual image hashes, as well as a simple way to deal with collisions. Anyone who is interested, please, under the cat.
Overview
There are many different approaches to creating a perceptual image hash. All of them are united by 3 main stages:
- Preliminary processing. At this stage, the image is reduced to a form in which it is easier to process to construct a hash. This can be the application of various filters (for example, Gauss), discoloration, image reduction, etc.
- Basic calculations. From the image obtained at stage 1, a matrix (or vector) is built. The matrix (vector) can be a matrix of frequencies (for example, after the Fourier transform), a histogram of luminances, or an even more simplified image.
- Building a hash. From the matrix (vector) obtained in stage 2, some (possibly all) coefficients are taken and converted to a hash. Usually a hash is obtained from 8 to ~ 100 bytes in size. The calculated hash values are then compared using functions that compute the "distance" between the two hashes.
In this publication, we will not concern the implementation of the above algorithms. It is an overview and talks about different approaches to building hashes.
Perceptual Hash Algorithms
We will look at 4 different hash algorithms: Simple Hash [4], DCT Based Hash [1], [11], Radial Variance Based Hash [1], [5] and Marr- Hildreth Operator Based Hash [1], [6] .
Simple Hash (aka Average Hash)
The essence of this algorithm is to display the average value of low frequencies. In images, high frequencies provide detail, while low frequencies show structure. Therefore, to build such a hash function, which for similar images will produce a close hash, you need to get rid of high frequencies. Principle of operation:
- Reduce the size. The fastest way to get rid of high frequencies is to reduce the image. The image is reduced to size in the range of 32x32 and 8x8.
- Remove color. A small image is translated in grayscale, so the hash is reduced by a factor of three.
- Calculate the average color value for all pixels.
- Build a chain of bits. For each pixel, the color is replaced by 1 or 0, depending on whether it is more or less than average.
- Build a hash. Translation of 1024 bits into one value. The order does not matter, but usually bits are written from left to right, from top to bottom.
The resulting hash is resistant to scaling, compressing or stretching the image, changing the brightness, contrast, color manipulation. But the main advantage of the algorithm is its speed. To compare hashes of this type, the normalized Hamming distance function is used.

Original Image

Received “Fingerprint”
Discrete Cosine Transform Based Hash (aka pHash)
The discrete cosine transform (DCT) [7] is one of the orthogonal transforms that is closely related to the discrete Fourier transform (DFT) and is a homomorphism of its vector space. DCT, like any Fourier-oriented transformation, expresses a function or signal (a sequence of a finite number of data points) as a sum of sinusoids with different frequencies and amplitudes. DCT uses only cosine functions, unlike DFT, which uses both cosine and sine functions. There are 8 types of DCT [7]. The most common is the second type. We will use it to build a hash function.
Let's see what the second type of DCT is:
Let x [m], where m = 0, ..., N - 1 is a sequence of signal lengths N. Define the second type of DCT, as
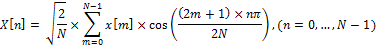
This expression can be rewritten as:
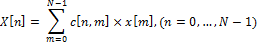
where c [n, m] is an element of the DCT matrix at the intersection of a row with number n and a column with number m.
DCT matrix is defined as:
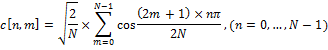
This matrix is very convenient for calculating DCT. DCT can be calculated in advance, for any required length. Thus, DCT can be represented in the form:
DCT = M × I × M '
Where M is the DCT matrix, I is the square-sized image, M' is the inverse matrix.
Low-frequency DCT coefficients are most stable to image manipulation. This is because most of the signal information is usually concentrated in several low-frequency coefficients. As a matrix I, an image is usually taken, compressed to a size of 32x32 and simplified using various filters, for example, bleaching. The result is a DCT matrix (I), in the upper left corner of which there are low-frequency coefficients. To build a hash, the upper left 8x8 frequency block is taken. Then, a 8-byte hash is built from this block by finding the middle and constructing a chain of bits (just like in Simple Based Hash).
We list the steps for constructing a hash using this algorithm:
- Remove color. To suppress unnecessary high frequencies;
- Apply a median filter [8] to reduce the noise level. At the same time, the image is divided into so-called “windows”, then each window is replaced by a median [9] for neighboring windows;
- Reduce the image to 32x32;
- Apply DCT to the image;
- Build a hash.
The main advantages of such a hash are resistance to small turns, blurring and compression of the image, as well as the speed of comparing hashes due to their small size. To compare hashes of this type, the Hamming distance function is used.
Radial Variance Based Hash
The idea of the Radial Variance Based Hash algorithm is to construct a ray dispersion vector (LDP) based on the Radon transform [5]. Then DCT is applied to the DVD and the hash is calculated. The Radon transform is an integral transform of the function of many variables along a straight line. It is resistant to image processing using various manipulations (e.g., compression) and geometric transformations (e.g., rotations). In the two-dimensional case, the Radon transform for the function f (x, y) looks like this:
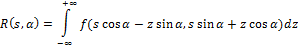
The Radon transform has a simple geometric meaning - it is the integral of the function along a straight line perpendicular to the vector n = (cos a, sin a) and passing at a distance s (measured along the vector n, with the corresponding sign) from the origin.

To expand the Radon transform for discrete images, the linear integral along the straight line d = x ∙ cos α + y ∙ sin α can be approximated by summing the values of all pixels lying in a line with a width of one pixel:
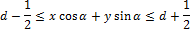
Later it was found that it is better to use the variance instead of the sum of the values pixels along the projection line [6]. Dispersion handles luminance gaps along the projection line much better. Such luminance gaps appear due to edges that are orthogonal to the projection line.
Now we define the ray vector of dispersion. Let Γ (α) be the set of pixels on the projection line corresponding to a given angle. Let (x ′, y ′) be the coordinates of the central pixel in the image. x, y belong to Γ (α) if and only if

Now we define the radial variance vector:
Let I (x, y) denote the brightness of the pixel (x, y), # Г (α) is the cardinality of the set, then the ray dispersion vector R [α], where α = 0,1, ..., 179 we define as
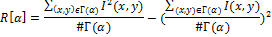
It is enough to construct the vector from 180 values of the angle, since the Radon transform is symmetric. The resulting vector can be used to construct a hash, but this algorithm proposes some more improvement - apply DCT to the resulting vector. The result is a vector that inherits all the important properties of DCT. The first 40 coefficients of the resulting vector, which correspond to low frequencies, are taken as a hash. Thus, the size of the received hash is 40 bytes.
So, we list the steps for constructing a hash using this algorithm:
- Remove color to suppress unnecessary high frequencies;
- Blurring an image (blurring) using the Gaussian blur [10]. The image is converted using the Gaussian function to suppress some noise;
- Apply gamma correction to eliminate image fading.
- Build a ray vector of dispersion;
- Apply DCT to the dispersion vector;
- Build a hash.
To compare hashes of this type, a peak search for the cross-correlation function is used.
Marr-Hildreth Operator Based Hash
The Marra-Hildreth operator [16] allows you to define the edges in the image. Generally speaking, a border in an image can be defined as an edge or contour separating adjacent portions of an image that have relatively excellent characteristics in accordance with certain features. These features can be color or texture, but most often the gray gradation of the image color (brightness) is used. The result of determining the boundaries is a border map. A border map describes the classification of borders for each pixel in an image. If the boundaries are defined as a sharp change in brightness, then derivatives or a gradient can be used to find them.
Let the function
 indicates the brightness level for the line (one-dimensional array of pixels). The first approach to determining the boundaries is to find local extrema of the function, that is, the first derivatives. The second approach (Laplace's method) is to find the second derivatives
indicates the brightness level for the line (one-dimensional array of pixels). The first approach to determining the boundaries is to find local extrema of the function, that is, the first derivatives. The second approach (Laplace's method) is to find the second derivatives  [1].
[1]. Both approaches can be adapted for the case of two-dimensional discrete images, but with some problems. To find the derivatives in the discrete case, approximation is required. In addition, noise in the image can significantly degrade the process of finding boundaries. Therefore, before determining the boundaries to the image, you need to apply some kind of filter that suppresses noise. To build a hash, you can choose an algorithm that uses the Laplace operator (approach 2) and a Gaussian filter.
We define a continuous Laplacian (Laplace operator):
Let
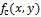 determines the brightness in the image. Then the continuous Laplacian is defined as:
determines the brightness in the image. Then the continuous Laplacian is defined as: 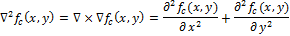
Zero
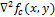 and there are points corresponding to the boundary of the function
and there are points corresponding to the boundary of the function 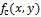 , since these are points at which the second derivative vanishes. Various filters (discrete Laplace operators) can be obtained from continuous Laplacian. Such a filter
, since these are points at which the second derivative vanishes. Various filters (discrete Laplace operators) can be obtained from continuous Laplacian. Such a filter 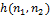 can be applied to a discrete image using the convolution of functions. The Laplace operator for an image
can be applied to a discrete image using the convolution of functions. The Laplace operator for an image 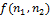 can be rewritten as:
can be rewritten as: 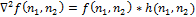
where * denotes a convolution of functions. To construct a map of boundaries, you need to find the zeros of the discrete operator
 .
.Now consider the Marra-Hildreth operator. It is also called the Laplacian from the Gauss filter (LoG) - this is a special type of discrete Laplace operator. LoG is constructed by applying the Laplace operator to a Gaussian filter (function). The peculiarity of this operator is that it can highlight borders on a certain scale. The scale variable can be varied in order to better identify the boundaries.
We define the Gaussian filter as:
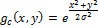
Convolution with the Laplace operation can be interchanged, because the derivative and convolution are linear operators:
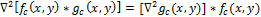
This property allows you to pre-calculate the operator
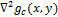 , because it does not depend on the image (
, because it does not depend on the image ( 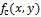 ).
). (Marra-Hildreth operator, Laplacian from the Gauss filter, LoG). LoG hc (x, y) is defined as:
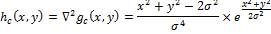
To use LoG in discrete form, we will discretize this equation by substituting the desired scale variable. By default, its value is taken as 1.0. Then the filter can be applied to the image using discrete convolution.
Define a discrete convolution:
Let x, y, z be the pixel width, length, and depth of the image I.
The result R of the convolution of the image I with the mask M is defined as:
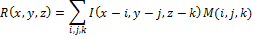
Now, we list the steps of the algorithm that uses the Marr-Hildreth operator to construct the hash:
- Remove color to suppress unnecessary high frequencies;
- Translate image in size 128x128;
- Blur image (blurring). The image is converted using the Gaussian function to suppress some noise [10];
- Build the Marra-Hildreth operator;
- Apply discrete convolution to LoG and image. You will get an
image on which brightness jumps are clearly visible; - Convert image to bar graph. The image is divided into small blocks (5x5), in which the brightness values are summed.
- Build a hash from a histogram. The histogram is divided into 3x3 blocks. For these blocks, the average brightness value is considered and the method of constructing a chain of bits is used. It turns out a binary hash of 64 bytes in size.
The size of the received hash is not small, however, comparing the two hashes takes quite a bit of time compared to the Radial algorithm, since the normalized Hamming distance function is used. Also, such an algorithm is sensitive to image rotations, but is resistant to scaling, darkening, and compression.
Perceptual Hash Value Comparison Functions
Hamming Distance
The Hamming distance determines the number of different positions between two binary sequences.
Definition:
Let A be an alphabet of finite length.
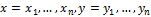 - binary sequences (vectors). We define the Hamming distance Δ between x and y as:
- binary sequences (vectors). We define the Hamming distance Δ between x and y as: 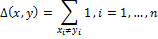
This method of comparing hash values is used in the DCT Based Hash method. The hash is 8 bytes in size, so the Hamming distance lies in the interval [0, 64]. The smaller the Δ value, the more similar the images.
To facilitate comparison, the Hamming distance can be normalized using the length of the vectors: The
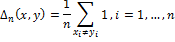
normalized Hamming distance is used in the Simple Hash and Marr-Hildreth Operator Based Hash algorithms. The Hamming distance lies in the interval [0.1] and the closer Δ is to 0, the more similar the images.
Peak cross-correlation function
The correlation between two signals is defined as:
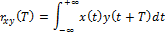
where x (t) and y (t) are two continuous functions of real numbers. The function rxy (t) describes the shift of these two signals relative to time T. The variable T determines how far the signal is shifted to the left. If the signals x (t) and y (t) are different, the function rxy T is called cross-correlation.
We define the Normalized cross-correlation function:
Let xi and yi, where i = 0, ... N - 1 are two sequences of real numbers, and N is the length of both sequences. The delayed armed formations d are defined as:
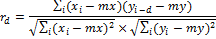
where mx and my denote the average value for the corresponding sequence.
The peak of the cross-correlation function (PCC) is the maximum value of the function rd that can be achieved in the interval d = 0, N.
PCC is used to compare hash values in the Radial Variance Based Hash algorithm. PCC ∈ [0,1], the greater its value, the more similar the images.
A few words about practice
We examined 4 different approaches in the implementation of hash algorithms. The scope of perceptual hashes is wide, from searching for similar images to detecting spam in pictures.
In our project, we use a perceptual hash to identify duplicate images. Moreover, it is often possible to successfully compare among themselves images containing watermark'i (obtained from different sources) or images with cropped edges.
The best algorithm for finding duplicates can be considered Radial Variance Based Hash, but it is extremely difficult to use on large amounts of data, due to the very time-consuming comparison of hashes.
For ourselves, we chose DCT based Hash. We use a 64-bit hash, this is enough to find duplicates, however such a small hash size inevitably leads to collisions. We are struggling with collisions by building a histogram (spectrum) for the image.
Each component of the spectrum means the relative number of colors of one or another subrange in the image, in other words, shows the distribution of colors in the image. It looks something like this:

Thus, we first look for images comparing the hash, and then compare the histograms, if the histograms are significantly different, then this image is not considered similar. The histograms themselves can be compared by considering the cross-correlation as well as when comparing the Radial Variance Based Hash, using Pearson cross-correlation:
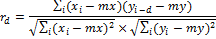
If this topic is of interest to the community, in the next article I will talk specifically about our implementation of DCT hash, as well as how to find the Hamming distance.
List of references
[1] Egmont-Petersen, M., de Ridder, D., Handels, H. «Image processing with
neural networks — a review». Pattern Recognition 35 (10), pp. 2279–2301(2002)
[2] Christoph Zauner. Implementation and Benchmarking of Perceptual Image
Hash Functions (2010)
[3] Locality-sensitive hashing.
en.wikipedia.org/wiki/Locality-sensitive_hashing
[4] Simple and DCT perceptual hash-algorithms.
www.hackerfactor.com/blog/index.php?/archives/432-Looks-Like-
It.html
[5] Standaert, F.X., Lefebvre, F., Rouvroy, G., Macq, B.M., Quisquater, J.J.,
and Legat, J.D.: Practical evaluation of a radial soft hash algorithm. In
Proceedings of the International Symposium on Information Technology:
Coding and Computing (ITCC), vol. 2, pp. 89-94. IEEE, Apr. 2005
[6] D. Marrand, E. Hildret. Theory of edge detection, pp. 187-215 (1979)
[7] en.wikipedia.org/wiki/Discrete_cosine_transform
[8] en.wikipedia.org/wiki/Median_filter
[9] en.wikipedia.org/wiki/Median
[10] en.wikipedia.org / wiki / Gaussian_blur
[11] Zeng Jie. A Novel Block-DCT and PCA Based Image Perceptual Hashing
Algorithm. IJCSI International Journal of Computer Science Issues, Vol. 10,
Issue 1, No 3, January 2013
[12] de.wikipedia.org/wiki/Marr-Hildreth-Operator
neural networks — a review». Pattern Recognition 35 (10), pp. 2279–2301(2002)
[2] Christoph Zauner. Implementation and Benchmarking of Perceptual Image
Hash Functions (2010)
[3] Locality-sensitive hashing.
en.wikipedia.org/wiki/Locality-sensitive_hashing
[4] Simple and DCT perceptual hash-algorithms.
www.hackerfactor.com/blog/index.php?/archives/432-Looks-Like-
It.html
[5] Standaert, F.X., Lefebvre, F., Rouvroy, G., Macq, B.M., Quisquater, J.J.,
and Legat, J.D.: Practical evaluation of a radial soft hash algorithm. In
Proceedings of the International Symposium on Information Technology:
Coding and Computing (ITCC), vol. 2, pp. 89-94. IEEE, Apr. 2005
[6] D. Marrand, E. Hildret. Theory of edge detection, pp. 187-215 (1979)
[7] en.wikipedia.org/wiki/Discrete_cosine_transform
[8] en.wikipedia.org/wiki/Median_filter
[9] en.wikipedia.org/wiki/Median
[10] en.wikipedia.org / wiki / Gaussian_blur
[11] Zeng Jie. A Novel Block-DCT and PCA Based Image Perceptual Hashing
Algorithm. IJCSI International Journal of Computer Science Issues, Vol. 10,
Issue 1, No 3, January 2013
[12] de.wikipedia.org/wiki/Marr-Hildreth-Operator
