Lossless data compression algorithms, part 2
Part 1
Many techniques have been invented for data compression. Most of them combine several compression principles to create a complete algorithm. Even good principles, when combined together, give the best result. Most techniques use the principle of entropy coding, but others are also common - Run-Length Encoding and Burrows-Wheeler Transform.
This is a very simple algorithm. It replaces a series of two or more identical characters with a number indicating the length of the series, followed by the symbol itself. Useful for very redundant data, such as pictures with a large number of identical pixels, or in combination with algorithms such as BWT.
Simple example:
Input: AAABBCCCCDEEEEEEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
Output: 3A2B4C1D6E38A
The algorithm, invented in 1994, reversibly transforms a data block so as to maximize the repetition of identical characters. He does not compress the data himself, but prepares it for more efficient compression via RLE or another compression algorithm.
Algorithm:
- create an array of strings
- create all possible transformations of the incoming data row, each of which is stored in the array
- sort the array
- return the last column
The algorithm works best with large data with many repeated characters. An example of working on a suitable data array (& indicates the end of the file)

Due to the alternation of identical characters, the output of the algorithm is optimal for RLE compression, which gives "3H & 3A". But on real data, unfortunately, such optimal results are usually not obtained.
Entropy in this case means the minimum number of bits, on average, required to represent a character. A simple EC combines the statistical model and the encoder itself. The input file is parsed to build a stat.model consisting of the probabilities of the appearance of certain characters. Then the encoder, using the model, determines which bit or byte encodings to assign to each character, so that the most common ones are represented by the shortest encodings, and vice versa.
One of the earliest techniques (1949). Creates a binary tree to represent the probabilities of occurrence of each of the characters. Then they are sorted so that the most common ones are at the top of the tree, and vice versa.
The code for the symbol is obtained by searching the tree, and adding 0 or 1, depending on whether we go left or right. For example, the path to “A” is two branches to the left and one to the right, its code will be “110”. The algorithm does not always give optimal codes because of the methodology for constructing a tree from the bottom up. Therefore, the Huffman algorithm is now used, suitable for any input.
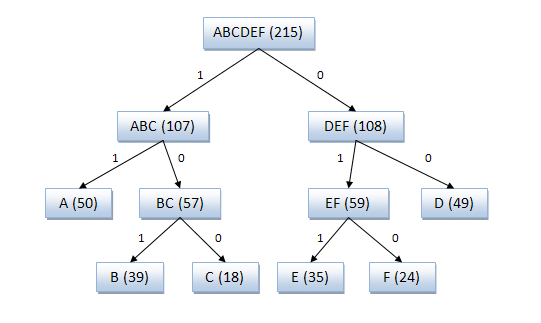
1. parse input, count the number of occurrences of all characters
2. determine the probability of occurrence of each of them
3. sort the characters by the probability of occurrence
4. divide the list in half so that the sum of the probabilities in the left branch is approximately equal to the sum in the right
5. add 0 or 1 for the left and right nodes respectively
6. repeat steps 4 and 5 for the right and left subtrees until each node will be a "sheet"
This is a variant of entropy coding that works similar to the previous algorithm, but the binary tree is built from top to bottom to achieve the optimal result.
1. Parse input, count the number of repetitions of characters
2. Determine the probability of occurrence of each character
3. Sort the list by probabilities (the most frequent at the beginning)
4. Create sheets for each character, and add them to the queue
5. while the queue consists of more than one symbol:
- we take two sheets from the queue with the least probabilities
- add 0 to the code of the first, 1
- to the code of the second - create a node with a probability equal to the sum of the probabilities of two nodes
- hang the first node on the left side, the second on the right
- add the received node to queue
6. The last node in the queue will be the root of the binary tree.
It was developed in 1979 by IBM for use in their mainframes. It achieves a very good compression ratio, usually greater than that of Huffman, but it is relatively complex compared to the previous ones.
Instead of dividing the probabilities into a tree, the algorithm converts the input into a single rational number from 0 to 1.
In general, the algorithm is as follows:
1. Count the number of unique characters at the input. This number will represent the basis for the notation b (b = 2 - binary, etc.).
2. calculate the total input length
3. assign “codes” from 0 to b to each of the unique characters in the order in which they appear
4. replace the characters with codes, getting a number in the number system with base b
5. convert the resulting number to a binary system
Example. At the input line “ABCDAABD”
1. 4 unique characters, base = 4, data length = 8
2. assign codes: A = 0, B = 1, C = 2, D = 3
3. get the number “0.01230013”
4. convert “0.01231123” from a quaternary to a binary system: 0.01101100000111
If we assume that we are dealing with eight-bit characters, then we have 8x8 = 64 bits at the input, and 15 at the output, that is, the compression ratio is 24%.
It all started with the LZ77 algorithm (1977), which introduced a new concept of “sliding window”, which allowed to significantly improve data compression. LZ77 uses a dictionary containing triples of data — offset, series length, and discrepancy symbol. Offset - how far from the beginning of the file the phrase is. Series length - how many characters, counting from the offset, belong to the phrase. The discrepancy symbol indicates that a new phrase has been found that is similar to the one indicated by the offset and length, except for this symbol. The dictionary changes as the file is parsed using a sliding window. For example, the window size can be 64 MB, then the dictionary will contain data from the last 64 megabytes of input data.
For example, for the input "abbadabba" the result would be "abb (0,1, 'd') (0,3, 'a')"
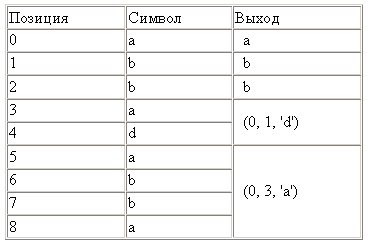
In this case, the result is longer than the input, but usually it is of course shorter.
A modification of the LZ77 algorithm proposed by Michael Rhode in 1981. Unlike LZ77, it works in linear time, but it requires more memory. Usually loses to LZ78 in compression.
Invented by Phil Katz in 1993, and is used by most modern archivers. It is a combination of LZ77 or LZSS with Huffman coding.
Patented DEFLATE variation with dictionary expansion up to 64 Kb. Compresses better and faster, but is not used everywhere, because not open.
The Lempel-Ziv-Storere-Zimanski algorithm was introduced in 1982. An improved version of LZ77, which calculates whether the size of the result will be increased by replacing the original data with encoded ones.
It is still used in popular archivers, for example RAR. Sometimes - to compress data during transmission over the network.
It was developed in 1987, stands for Lempel-Ziv-Huffman. A variation of LZSS, uses Huffman coding to compress pointers. Compresses a little better, but significantly slower.
Developed in 1987 by Timothy Bell, as an option to LZSS. Like LZ, LZB reduces the resulting file size by efficiently encoding pointers. This is achieved by gradually increasing the size of the pointers while increasing the size of the sliding window. Compression is higher than LZSS and LZH, but the speed is much lower.
Decrypted as “Lempel-Ziv with Reduced Offset,” improves the LZ77 algorithm by decreasing the offset to reduce the amount of data needed to encode the offset-length pair. It was first introduced in 1991 in the LZRW4 algorithm from Ross Williams. Other variations are BALZ, QUAD, and RZM. A well-optimized ROLZ achieves almost the same compression rates as LZMA - but it has not gained popularity.
"Lempel Ziv with the prediction." ROLZ variation with offset = 1. There are several options, some aimed at compression speed, others at the degree. The LZW4 algorithm uses arithmetic coding for the best compression.
An algorithm from Ron Williams in 1991, where he first introduced the concept of offset reduction. Achieves high compression ratios at decent speed. Then Williams made variations of LZRW1-A, 2, 3, 3-A, and 4
A variation from Jeff Bonwick (hence the “JB”) from 1998, for use on the Solaris Z File System (ZFS) file system. A variant of the LZRW1 algorithm, redesigned for high speeds, as required by the use of the file system and the speed of disk operations.
Lempel-Ziv-Stac, developed by Stac Electronics in 1994 for use in disk compression programs. A LZ77 modification that distinguishes between characters and length-offset pairs, in addition to deleting the next character encountered. Very similar to LZSS.
It was developed in 1995 by J. Forbes and T. Potanen for Amiga. Forbes sold the algorithm to Microsoft in 1996, and got a job there, as a result of which his improved version was used in the files CAB, CHM, WIM and Xbox Live Avatars.
Designed in 1996 by Marcus Oberhumer with an eye on compression and decompression speeds. Allows you to adjust compression levels, consumes very little memory. Looks like LZSS.
“Lempel-Ziv Markov chain Algorithm”, appeared in 1998 in the 7-zip archiver, which demonstrated compression better than almost all archivers. The algorithm uses a chain of compression methods to achieve the best result. Initially, a slightly modified LZ77 working at the bit level (unlike the usual method of working with bytes) parses data. Its output is subjected to arithmetic coding. Then other algorithms can be applied. The result is the best compression among all archivers.
The next version of LZMA, from 2009, uses multithreading and stores incompressible data a little more efficiently.
The concept, created in 2001, proposes a statistical analysis of data in combination with LZ77 to optimize the codes stored in the dictionary.
Algorithm of 1978, authors - Lempel and Ziv. Instead of using a sliding window to create a dictionary, the dictionary is compiled by parsing data from a file. Dictionary size is usually measured in a few megabytes. The differences in the variants of this algorithm are based on what to do when the dictionary is full.
When parsing a file, the algorithm adds each new character or combination of them to the dictionary. For each character in the input, a dictionary form is created (index + unknown character) in the output. If the first character of the string is already in the dictionary, we look for the substrings of this string in the dictionary, and the longest is used to build the index. The data pointed to by the index is appended to the last character of the unknown substring. If the current character is not found, the index is set to 0, indicating that this is an occurrence of a single character in the dictionary. Entries form a linked list.
The input "abbadabbaabaad" on the output will give "(0, a) (0, b) (2, a) (0, d) (1, b) (3, a) (6, d)"
An input such as " abbadabbaabaad "would generate the output" (0, a) (0, b) (2, a) (0, d) (1, b) (3, a) (6, d) ". You can see how this was derived in the following example:

Lempel-Ziv-Welch, 1984. The most popular version of the LZ78, despite the patenting. The algorithm gets rid of extra characters in the output and the data consists only of pointers. It also saves all the characters of the dictionary before compression and uses other tricks to improve compression - for example, encoding the last character of the previous phrase as the first character of the next. Used in GIFs, early versions of ZIP and other special applications. Very fast, but loses in compression to newer algorithms.
The compression of Lempel-Ziv. LZW modification used in UNIX utilities. It monitors the compression ratio, and as soon as it exceeds the specified limit, the dictionary is redone again.
Lempel-Ziv-Tischer. When the dictionary is filled, it deletes the phrases that were used less often than all, and replaces them with new ones. Not gained popularity.
Victor Miller and Mark Wegman, 1984. Acts as LZT, but combines not similar data in the dictionary, but the last two phrases. As a result, the dictionary grows faster, and you have to get rid of rarely used phrases more often. Also unpopular.
James Storer, 1988. Modification of LZMW. “AP” means “all prefixes” - instead of saving one phrase at each iteration, every change is saved in the dictionary. For example, if the last phrase was “last” and the current one was “next”, then “lastn”, “lastne”, “lastnex”, “lastnext” are stored in the dictionary.
A 2006 version of LZW that works with character combinations rather than single characters. Successfully works with datasets that contain frequently repeated character combinations, such as XML. Commonly used with a preprocessor splitting data into combinations.
1985, Matti Jacobson. One of the few LZ78 variants that differ from the LZW. Saves each unique line in already processed input data, and assigns unique codes to all of them. When filling out a dictionary, single entries are deleted from it.
Partial Match Prediction - uses the data already processed to predict which character will be next in the sequence, thereby reducing the entropy of the output. It is usually combined with an arithmetic encoder or adaptive Huffman coding. PPMd variation used in RAR and 7-zip
An open source implementation of BWT. With ease of implementation, it achieves a good compromise between speed and compression ratio, which is why it is popular on UNIX. First, the data is processed using RLE, then BWT, then the data is sorted in a special way to get long sequences of identical characters, after which RLE is applied again. And finally, the Huffman encoder completes the process.
Matt Mahoney, 2002 Improvement of PPM (d). Improves them with the help of an interesting technique called “context mixing”. In this technique, several predictive algorithms are combined to improve the prediction of the next symbol. Now it is one of the most promising algorithms. Since its first implementation, two dozen options have already been created, some of which set compression records. Minus - low speed due to the need to use several models. An option called PAQ80 supports 64 bits and shows a serious improvement in speed (used, in particular, in the PeaZip program for Windows).
Data Compression Techniques
Many techniques have been invented for data compression. Most of them combine several compression principles to create a complete algorithm. Even good principles, when combined together, give the best result. Most techniques use the principle of entropy coding, but others are also common - Run-Length Encoding and Burrows-Wheeler Transform.
Series Length Coding (RLE)
This is a very simple algorithm. It replaces a series of two or more identical characters with a number indicating the length of the series, followed by the symbol itself. Useful for very redundant data, such as pictures with a large number of identical pixels, or in combination with algorithms such as BWT.
Simple example:
Input: AAABBCCCCDEEEEEEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
Output: 3A2B4C1D6E38A
Burroughs-Wheeler Transformation (BWT)
The algorithm, invented in 1994, reversibly transforms a data block so as to maximize the repetition of identical characters. He does not compress the data himself, but prepares it for more efficient compression via RLE or another compression algorithm.
Algorithm:
- create an array of strings
- create all possible transformations of the incoming data row, each of which is stored in the array
- sort the array
- return the last column
The algorithm works best with large data with many repeated characters. An example of working on a suitable data array (& indicates the end of the file)

Due to the alternation of identical characters, the output of the algorithm is optimal for RLE compression, which gives "3H & 3A". But on real data, unfortunately, such optimal results are usually not obtained.
Entropy coding
Entropy in this case means the minimum number of bits, on average, required to represent a character. A simple EC combines the statistical model and the encoder itself. The input file is parsed to build a stat.model consisting of the probabilities of the appearance of certain characters. Then the encoder, using the model, determines which bit or byte encodings to assign to each character, so that the most common ones are represented by the shortest encodings, and vice versa.
Shannon - Fano Algorithm
One of the earliest techniques (1949). Creates a binary tree to represent the probabilities of occurrence of each of the characters. Then they are sorted so that the most common ones are at the top of the tree, and vice versa.
The code for the symbol is obtained by searching the tree, and adding 0 or 1, depending on whether we go left or right. For example, the path to “A” is two branches to the left and one to the right, its code will be “110”. The algorithm does not always give optimal codes because of the methodology for constructing a tree from the bottom up. Therefore, the Huffman algorithm is now used, suitable for any input.

1. parse input, count the number of occurrences of all characters
2. determine the probability of occurrence of each of them
3. sort the characters by the probability of occurrence
4. divide the list in half so that the sum of the probabilities in the left branch is approximately equal to the sum in the right
5. add 0 or 1 for the left and right nodes respectively
6. repeat steps 4 and 5 for the right and left subtrees until each node will be a "sheet"
Huffman coding
This is a variant of entropy coding that works similar to the previous algorithm, but the binary tree is built from top to bottom to achieve the optimal result.
1. Parse input, count the number of repetitions of characters
2. Determine the probability of occurrence of each character
3. Sort the list by probabilities (the most frequent at the beginning)
4. Create sheets for each character, and add them to the queue
5. while the queue consists of more than one symbol:
- we take two sheets from the queue with the least probabilities
- add 0 to the code of the first, 1
- to the code of the second - create a node with a probability equal to the sum of the probabilities of two nodes
- hang the first node on the left side, the second on the right
- add the received node to queue
6. The last node in the queue will be the root of the binary tree.
Arithmetic coding
It was developed in 1979 by IBM for use in their mainframes. It achieves a very good compression ratio, usually greater than that of Huffman, but it is relatively complex compared to the previous ones.
Instead of dividing the probabilities into a tree, the algorithm converts the input into a single rational number from 0 to 1.
In general, the algorithm is as follows:
1. Count the number of unique characters at the input. This number will represent the basis for the notation b (b = 2 - binary, etc.).
2. calculate the total input length
3. assign “codes” from 0 to b to each of the unique characters in the order in which they appear
4. replace the characters with codes, getting a number in the number system with base b
5. convert the resulting number to a binary system
Example. At the input line “ABCDAABD”
1. 4 unique characters, base = 4, data length = 8
2. assign codes: A = 0, B = 1, C = 2, D = 3
3. get the number “0.01230013”
4. convert “0.01231123” from a quaternary to a binary system: 0.01101100000111
If we assume that we are dealing with eight-bit characters, then we have 8x8 = 64 bits at the input, and 15 at the output, that is, the compression ratio is 24%.
Algorithm Classification
Algorithms Using the Sliding Window Method
It all started with the LZ77 algorithm (1977), which introduced a new concept of “sliding window”, which allowed to significantly improve data compression. LZ77 uses a dictionary containing triples of data — offset, series length, and discrepancy symbol. Offset - how far from the beginning of the file the phrase is. Series length - how many characters, counting from the offset, belong to the phrase. The discrepancy symbol indicates that a new phrase has been found that is similar to the one indicated by the offset and length, except for this symbol. The dictionary changes as the file is parsed using a sliding window. For example, the window size can be 64 MB, then the dictionary will contain data from the last 64 megabytes of input data.
For example, for the input "abbadabba" the result would be "abb (0,1, 'd') (0,3, 'a')"

In this case, the result is longer than the input, but usually it is of course shorter.
Lzr
A modification of the LZ77 algorithm proposed by Michael Rhode in 1981. Unlike LZ77, it works in linear time, but it requires more memory. Usually loses to LZ78 in compression.
Deflate
Invented by Phil Katz in 1993, and is used by most modern archivers. It is a combination of LZ77 or LZSS with Huffman coding.
Deflate64
Patented DEFLATE variation with dictionary expansion up to 64 Kb. Compresses better and faster, but is not used everywhere, because not open.
Lzss
The Lempel-Ziv-Storere-Zimanski algorithm was introduced in 1982. An improved version of LZ77, which calculates whether the size of the result will be increased by replacing the original data with encoded ones.
It is still used in popular archivers, for example RAR. Sometimes - to compress data during transmission over the network.
Lh
It was developed in 1987, stands for Lempel-Ziv-Huffman. A variation of LZSS, uses Huffman coding to compress pointers. Compresses a little better, but significantly slower.
Lzb
Developed in 1987 by Timothy Bell, as an option to LZSS. Like LZ, LZB reduces the resulting file size by efficiently encoding pointers. This is achieved by gradually increasing the size of the pointers while increasing the size of the sliding window. Compression is higher than LZSS and LZH, but the speed is much lower.
Roolz
Decrypted as “Lempel-Ziv with Reduced Offset,” improves the LZ77 algorithm by decreasing the offset to reduce the amount of data needed to encode the offset-length pair. It was first introduced in 1991 in the LZRW4 algorithm from Ross Williams. Other variations are BALZ, QUAD, and RZM. A well-optimized ROLZ achieves almost the same compression rates as LZMA - but it has not gained popularity.
Lzp
"Lempel Ziv with the prediction." ROLZ variation with offset = 1. There are several options, some aimed at compression speed, others at the degree. The LZW4 algorithm uses arithmetic coding for the best compression.
LZRW1
An algorithm from Ron Williams in 1991, where he first introduced the concept of offset reduction. Achieves high compression ratios at decent speed. Then Williams made variations of LZRW1-A, 2, 3, 3-A, and 4
Lzjb
A variation from Jeff Bonwick (hence the “JB”) from 1998, for use on the Solaris Z File System (ZFS) file system. A variant of the LZRW1 algorithm, redesigned for high speeds, as required by the use of the file system and the speed of disk operations.
Lzs
Lempel-Ziv-Stac, developed by Stac Electronics in 1994 for use in disk compression programs. A LZ77 modification that distinguishes between characters and length-offset pairs, in addition to deleting the next character encountered. Very similar to LZSS.
Lzx
It was developed in 1995 by J. Forbes and T. Potanen for Amiga. Forbes sold the algorithm to Microsoft in 1996, and got a job there, as a result of which his improved version was used in the files CAB, CHM, WIM and Xbox Live Avatars.
Lzo
Designed in 1996 by Marcus Oberhumer with an eye on compression and decompression speeds. Allows you to adjust compression levels, consumes very little memory. Looks like LZSS.
LZMA
“Lempel-Ziv Markov chain Algorithm”, appeared in 1998 in the 7-zip archiver, which demonstrated compression better than almost all archivers. The algorithm uses a chain of compression methods to achieve the best result. Initially, a slightly modified LZ77 working at the bit level (unlike the usual method of working with bytes) parses data. Its output is subjected to arithmetic coding. Then other algorithms can be applied. The result is the best compression among all archivers.
LZMA2
The next version of LZMA, from 2009, uses multithreading and stores incompressible data a little more efficiently.
Lempel-Ziv Statistical Algorithm
The concept, created in 2001, proposes a statistical analysis of data in combination with LZ77 to optimize the codes stored in the dictionary.
Dictionary Algorithms
Lz78
Algorithm of 1978, authors - Lempel and Ziv. Instead of using a sliding window to create a dictionary, the dictionary is compiled by parsing data from a file. Dictionary size is usually measured in a few megabytes. The differences in the variants of this algorithm are based on what to do when the dictionary is full.
When parsing a file, the algorithm adds each new character or combination of them to the dictionary. For each character in the input, a dictionary form is created (index + unknown character) in the output. If the first character of the string is already in the dictionary, we look for the substrings of this string in the dictionary, and the longest is used to build the index. The data pointed to by the index is appended to the last character of the unknown substring. If the current character is not found, the index is set to 0, indicating that this is an occurrence of a single character in the dictionary. Entries form a linked list.
The input "abbadabbaabaad" on the output will give "(0, a) (0, b) (2, a) (0, d) (1, b) (3, a) (6, d)"
An input such as " abbadabbaabaad "would generate the output" (0, a) (0, b) (2, a) (0, d) (1, b) (3, a) (6, d) ". You can see how this was derived in the following example:

Lzw
Lempel-Ziv-Welch, 1984. The most popular version of the LZ78, despite the patenting. The algorithm gets rid of extra characters in the output and the data consists only of pointers. It also saves all the characters of the dictionary before compression and uses other tricks to improve compression - for example, encoding the last character of the previous phrase as the first character of the next. Used in GIFs, early versions of ZIP and other special applications. Very fast, but loses in compression to newer algorithms.
Lzc
The compression of Lempel-Ziv. LZW modification used in UNIX utilities. It monitors the compression ratio, and as soon as it exceeds the specified limit, the dictionary is redone again.
Lzt
Lempel-Ziv-Tischer. When the dictionary is filled, it deletes the phrases that were used less often than all, and replaces them with new ones. Not gained popularity.
Lzmw
Victor Miller and Mark Wegman, 1984. Acts as LZT, but combines not similar data in the dictionary, but the last two phrases. As a result, the dictionary grows faster, and you have to get rid of rarely used phrases more often. Also unpopular.
Lzap
James Storer, 1988. Modification of LZMW. “AP” means “all prefixes” - instead of saving one phrase at each iteration, every change is saved in the dictionary. For example, if the last phrase was “last” and the current one was “next”, then “lastn”, “lastne”, “lastnex”, “lastnext” are stored in the dictionary.
Lzwl
A 2006 version of LZW that works with character combinations rather than single characters. Successfully works with datasets that contain frequently repeated character combinations, such as XML. Commonly used with a preprocessor splitting data into combinations.
Lzj
1985, Matti Jacobson. One of the few LZ78 variants that differ from the LZW. Saves each unique line in already processed input data, and assigns unique codes to all of them. When filling out a dictionary, single entries are deleted from it.
Non-Dictionary Algorithms
PPM
Partial Match Prediction - uses the data already processed to predict which character will be next in the sequence, thereby reducing the entropy of the output. It is usually combined with an arithmetic encoder or adaptive Huffman coding. PPMd variation used in RAR and 7-zip
bzip2
An open source implementation of BWT. With ease of implementation, it achieves a good compromise between speed and compression ratio, which is why it is popular on UNIX. First, the data is processed using RLE, then BWT, then the data is sorted in a special way to get long sequences of identical characters, after which RLE is applied again. And finally, the Huffman encoder completes the process.
PAQ
Matt Mahoney, 2002 Improvement of PPM (d). Improves them with the help of an interesting technique called “context mixing”. In this technique, several predictive algorithms are combined to improve the prediction of the next symbol. Now it is one of the most promising algorithms. Since its first implementation, two dozen options have already been created, some of which set compression records. Minus - low speed due to the need to use several models. An option called PAQ80 supports 64 bits and shows a serious improvement in speed (used, in particular, in the PeaZip program for Windows).
