How does the camera rotate in 3D games or what is the rotation matrix
In this article, I will briefly describe how exactly the coordinates of the points are converted when the camera is rotated in 3D games, css-transformations, and generally wherever there are any rotations of the camera or objects in space. In combination, this will be a brief introduction to linear algebra: the reader will know what (in fact) is a vector, a scalar product, and, finally, a rotation matrix.
Task. Suppose we have a two-dimensional picture, as below (house).
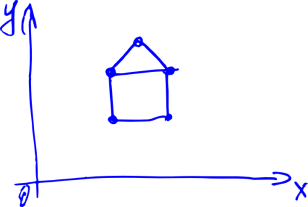
Suppose also that we look at the house from the origin in the direction of OX. Now we have turned a certain angle counterclockwise. Question: what will the house look like for us? Intuitively, the result will be approximately the same as in the picture below.
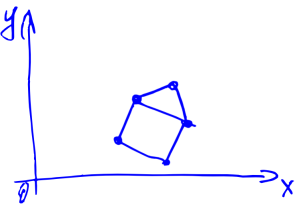
But how to calculate the result? And, worst of all, how to do it in three-dimensional space? If, for example, we rotate the camera very cunningly: first along the OZ axis, then OX, then OY?
The answers to these questions will be given in the article below. First, I will tell you how to represent the house in the form of numbers (that is, I will talk about vectors), then about what angles between vectors (that is, about a scalar product) are, and finally, how to rotate the camera (about the rotation matrix).
Let's think about vectors. That is, about arrows with length and direction.
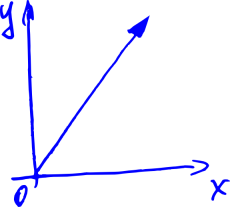
Applied to computer graphics — each such arrow defines a point in space.
We also want to learn to rotate them. Because when we turn all the arrows in the picture above, we turn the house. Let's imagine that all we can do with these arrows is add and multiply by a number. Like in school: to add two vectors, you need to draw a line from the beginning of the first vector to the end of the second.
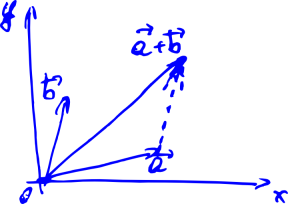
For now, we will focus on two-dimensional vectors. To begin with, we would like to learn how to write down these vectors somehow through numbers, because every time drawing them on paper in the form of arrows is not very convenient.
We learn how to do this, remembering that any vector can be represented as the sum of some special vectors (OX and OY), possibly multiplied by certain coefficients. These special vectors are called basic, and the coefficients are nothing more than the coordinates of our vector. If we denote the basis vectors by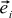 (here, i is the index of the vector, it is either 1 or 2), the vector in question is considered as
(here, i is the index of the vector, it is either 1 or 2), the vector in question is considered as 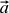 , and the coordinates of the latter as
, and the coordinates of the latter as 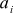 , then we obtain the formula
, then we obtain the formula
(1)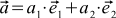
It can be shown that these coordinates will be unique for this basis .
The benefits of assigning coordinates to our arrows are obvious — before, you had to constantly draw an arrow to describe a vector, and now you just need to write two numbers — the coordinates of this vector. For example, we can agree to write something like this: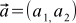 . Or this:
. Or this: 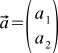 . Then
. Then 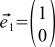 , a
, a  . Wonderful.
. Wonderful.
In real math, the procedure is slightly different. First, we describe the properties that any objects must satisfy, so that we call them vectors. They are very natural. For example, vectors must support the addition (two vectors) and multiplication by a number operation. The sum of two vectors should not depend on the order of the terms. The sum of the three vectors should not depend on the order in which we add them in pairs. And so on. The full list is on Wikipedia..
If our pieces of any kind satisfy these properties, then these pieces can be called vectors (this is duck typing). And the whole set of these pieces is a vector or linear space. The properties above are called axioms, and from them all other properties of vectors (or linear space) are deduced — hence the name “ linear algebra"). For example, it can be deduced that among the vectors there will exist such special basis vectors through which any vector can be expressed by formula (1) and that this expansion into coordinates will be unique for this basis. You can quickly show that our arrows just satisfy these axioms. The axiomatic approach is convenient, because if we come across some other objects that satisfy the axioms, then we can immediately apply all the results of our theory to them. In addition, this way we avoid the definitions of arrows on the fingers at the beginning of the theory.
It can be easily shown (from the very axioms) that when the vectors are added, their corresponding coordinates will be added, and when the vector is multiplied by a number, all coordinates are multiplied by the same number. Now, to add two vectors, as in the picture below, we can not draw them (and does not lead the line from the start of the first vector to the end of the second), and to write, for example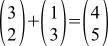 .
.

Let's now introduce a special function of two arbitrary vectors a and b, which we will call the scalar product. We shall denote it like this: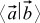 . These trendy brackets are scientifically called bra and ket vectors . There is no benefit from them yet, but it looks great — in addition, this notation still has a deep meaning, especially if you go into mathematical details or quantum mechanics.
. These trendy brackets are scientifically called bra and ket vectors . There is no benefit from them yet, but it looks great — in addition, this notation still has a deep meaning, especially if you go into mathematical details or quantum mechanics.
In the spirit of our axiomatic approach, we only require that the scalar product satisfy several axioms . If instead of the first vector we take the sum of vectors of the type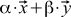 , then we want
, then we want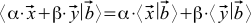 . Here, Greek letters are factors, x and y are vectors. We also want that if we substitute such a sum instead of the second vector, then we can make the same transformations (the scalar product of the sum of vectors also turns out to be the sum of scalar products, and the factors are also taken out of brackets). In addition, we want the values to
. Here, Greek letters are factors, x and y are vectors. We also want that if we substitute such a sum instead of the second vector, then we can make the same transformations (the scalar product of the sum of vectors also turns out to be the sum of scalar products, and the factors are also taken out of brackets). In addition, we want the values to 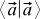 always be non-negative. Finally, we want it to be
always be non-negative. Finally, we want it to be 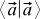 zero if and only if the vector itself is
zero if and only if the vector itself is 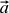 zero. Oh yes, and more so
zero. Oh yes, and more so 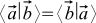 .
.
If we add a ruler and a protractor to our arrows on paper, then the function known from school will satisfy these axioms: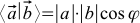 where the lengths of the vectors are measured by a ruler, the angle between the vectors is a
where the lengths of the vectors are measured by a ruler, the angle between the vectors is a 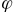 protractor.
protractor.
If the ruler and protractor we do not, then the scalar product can be defined length vektora-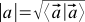 s angle between the vectors
s angle between the vectors 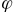 :
: 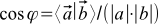 . Of course, the angle depends on the method of determining the scalar product.
. Of course, the angle depends on the method of determining the scalar product.
Let's see how the scalar product is expressed through the individual coordinates of the vectors. Suppose we have two vectors a and b that look like this: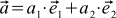 ,
, 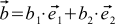 . Then
. Then 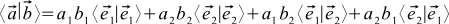 .
.
It doesn’t look very good. To make life better, we will continue to work only with special coordinate systems. We will choose only those coordinate systems in which the basis vectors have unit length and are perpendicular to each other. In other words,
(2a)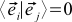 if
if 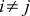
(2b)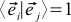 if
if 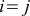
Such vectors are called orthonormal. The expression for the scalar product in orthonormal coordinate systems is transformed beyond recognition:
(3)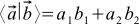
All coordinate systems in this article are assumed to be orthonormal. Surprisingly, it follows from our construction that the result of formula (3) does not depend on which orthonormal basis for coordinates to choose.
By carefully looking at the picture “Decomposition of the vector into coordinates” (it is given again after this paragraph), one can suspect that the coordinate of the vector is nothing more than its projection onto the corresponding base vector. That is, the value of the scalar product of the original vector with one of the basis vectors:
(4)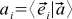

Indeed, for example,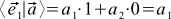 . This seems to be a tautology, because the coordinates of the basis vectors in their own basis will always be (1, 0) and (0, 1). But we can take other basis vectors, and express them through the old basis. For example, a new orthonormal basis may look like in the old basis
. This seems to be a tautology, because the coordinates of the basis vectors in their own basis will always be (1, 0) and (0, 1). But we can take other basis vectors, and express them through the old basis. For example, a new orthonormal basis may look like in the old basis 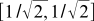 and
and 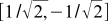 . And then we can determine, for example, the first coordinate of the vector
. And then we can determine, for example, the first coordinate of the vector 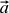 in the new basis by the formula (4) as
in the new basis by the formula (4) as 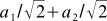 .
.
A meticulous reader will say "but formula (3) can be used as a definition of a scalar product, and then we do not need any orthonormalization of basis vectors." And it will be right that formula (3) can work as one of the definitions of a scalar product. But there is a subtle point: then we need to show that when the coordinate system changes, the same formula, but with the coordinates of the vectors a and b from another basis, will give the same number. And this will be only if all the bases are orthonormal. This can be shown by reading the next section.
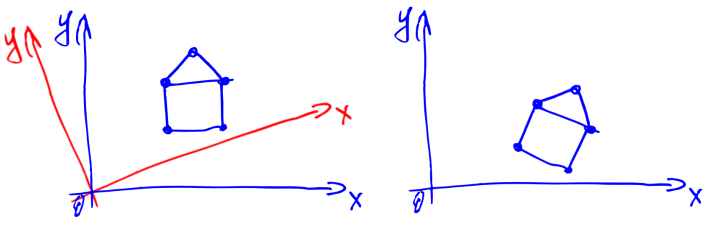
Let's find out how the coordinates of the vectors change if we change the entire coordinate system. Why do we even need to change the coordinate system? If you think a little, it will become clear that the rotation of the coordinate system is equivalent to the rotation of the camera in 3D or 2D modeling (see a slightly modified picture with a house below). So learning how to rotate a coordinate system is just what we need.
Let's denote the i-th coordinate of the vector a in the new coordinate system as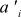 , and the new basis vectors as
, and the new basis vectors as 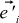 . In addition, we denote the jth coordinate of the OLD basis vector i in the NEW basis as
. In addition, we denote the jth coordinate of the OLD basis vector i in the NEW basis as 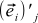 . Finally, we denote the ith coordinate of the NEW basis vector j in the OLD basis as
. Finally, we denote the ith coordinate of the NEW basis vector j in the OLD basis as . Now we can express the original vector and the old basis vectors through the new basis vectors. Namely,
. Now we can express the original vector and the old basis vectors through the new basis vectors. Namely,
(5)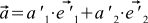 and
and
(6)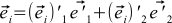
In addition, new basic vectors can be expressed in terms of the old ones:
(7)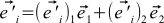
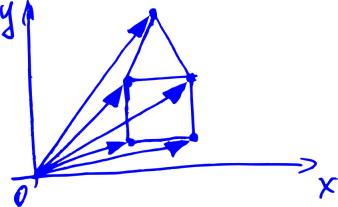
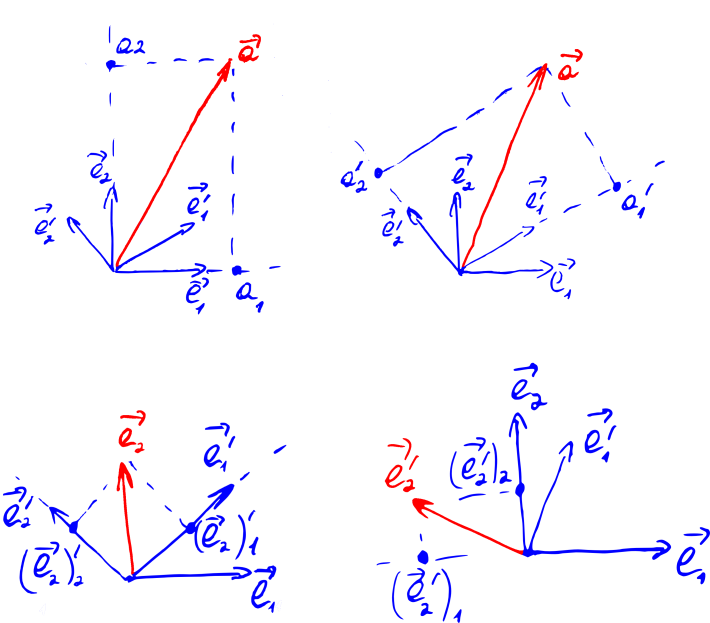
Some of these expansions are shown in the picture below.
Now we simply rewrite formula (1) through the vectors of the new basis:
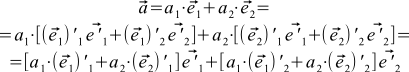
If we compare this with formula (5), and recall that the coordinates of the vectors are uniquely determined, we can see that
(8)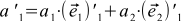 and it is
and it is 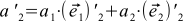
amazing how these formulas look like equations (3 )! They look like a scalar product of a vector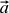 with certain vectors (we will show below that this is not accidental).
with certain vectors (we will show below that this is not accidental).
If we write equations (9) with one formula, we get
(9)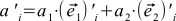
can derive this formula differently combining (4), (1) and (7)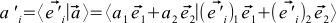 . If we recall the properties of the scalar product, then this formula splits into four sums. If now we recall that our basis vectors are orthonormal, we obtain
. If we recall the properties of the scalar product, then this formula splits into four sums. If now we recall that our basis vectors are orthonormal, we obtain 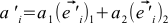 .
.
This formula does not look exactly like formula (9):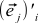 they stand instead
they stand instead 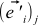 . This is not a mistake — simple
. This is not a mistake — simple 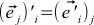 . Ie j Star OLD coordinate basis vector i in the new basis
. Ie j Star OLD coordinate basis vector i in the new basis 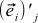 is always equal to the i -th coordinates of the new basis vector j in the old basis,
is always equal to the i -th coordinates of the new basis vector j in the old basis, 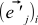 . This will become obvious if you try to express these coordinates through the formula (4):
. This will become obvious if you try to express these coordinates through the formula (4):
(10)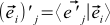 ,
,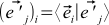
And the scalar product, as we recall, does not depend on the order of the product of vectors.
This will become even more obvious if we recall that these scalar products are the angles between different (unit) basis vectors. These angles, of course, are independent of whether to set them aside clockwise or counterclockwise.
If you are familiar with matrices, then formula (9) (two formulas) can be rewritten in matrix form
(11)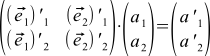
What does this all mean ?! As usual, there is no magic here — we just agree that the multiplication of this plate from the numbers on the left to the vector on the right is calculated as formula (9). That is, we multiply each row of the label by a column to the right (as if we are doing the scalar product of two vectors), and write the results under each other, also getting a column.
By the way, we can extend this rule to the multiplication of two labels: we agree to multiply each row of the first label by each column of the second, and also write the results in the label: we multiply the first row with the third column in the first row and third column. Formula (11) then becomes a special case of this rule. Schematically, this is all depicted in the figure below.
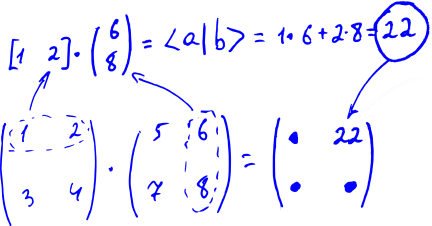
The tablets of numbers equipped with this rule of multiplication by vectors and other tablets will be called matrices.
The rule of matrix multiplication looks even more natural if we learn that the scalar product, as we agreed to denote it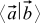 , in fact assumes that the vector a is a string, and the vector b-column. Before that, we agreed to write vectors in columns, and the row vector a is actually not just an inverted vector a , but an object of a special dual vector space . But in the case of orthonormal bases, the coordinates of the original and dual vectors coincide (that is, the a-row and a-column are the same), so these details do not affect our presentation. Everything is fine. In addition, on the other hand, formula (3) for the scalar product is a special case of matrix multiplication.
, in fact assumes that the vector a is a string, and the vector b-column. Before that, we agreed to write vectors in columns, and the row vector a is actually not just an inverted vector a , but an object of a special dual vector space . But in the case of orthonormal bases, the coordinates of the original and dual vectors coincide (that is, the a-row and a-column are the same), so these details do not affect our presentation. Everything is fine. In addition, on the other hand, formula (3) for the scalar product is a special case of matrix multiplication.
In general, it can be shown that multiplication by matrices corresponds to certain transformations of vectors. Instead of "transformation" it is customary to say operators. And matrix multiplication is a linear operator. In addition, for any linear operator, there is one and only one operator matrix. You can read about what it is on Wikipedia . If you describe it here, then the article will never end.
So, as we found out, the rotation of the coordinate system is equivalent to the rotation of the camera in 3D or 2D modeling. Therefore, the matrix from formula (11) is called the rotation matrix. Formula (11) can be interpreted not as a replacement of the coordinate system, but as a description of the rotation operator.
It is not yet clear how to calculate this matrix. This is not difficult if we turn to formulas (10) and recall that the cosine of the angle between unit vectors is equal to their scalar product. Then, for example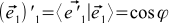 , where
, where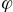 —The angle of rotation of the coordinate system (camera). It is, by definition, positive if the rotation is counterclockwise, and negative if it is rotated clockwise (see the figure below — it was already there, but now it is relevant again). If you tinker a bit with geometry or trigonometry, you can find out that the entire rotation matrix looks like this:
—The angle of rotation of the coordinate system (camera). It is, by definition, positive if the rotation is counterclockwise, and negative if it is rotated clockwise (see the figure below — it was already there, but now it is relevant again). If you tinker a bit with geometry or trigonometry, you can find out that the entire rotation matrix looks like this:
(12a)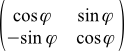
If you look at Wikipedia , the formula there looks a little different:
(12b)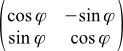
This is all because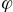 in it is the angle of rotation of the vectors themselves (or our objects such as a house). It is also considered positive if the rotation occurs counterclockwise. But the rotation of the camera is opposite to the rotation of objects, that is, the angle of rotation of the camera is equal to the angle of rotation of the objects, but taken with the opposite sign.
in it is the angle of rotation of the vectors themselves (or our objects such as a house). It is also considered positive if the rotation occurs counterclockwise. But the rotation of the camera is opposite to the rotation of objects, that is, the angle of rotation of the camera is equal to the angle of rotation of the objects, but taken with the opposite sign.
Again current drawing:

These matrices are very convenient things. They can be multiplied and added, moreover, not only two, but three and four. Matrices can be denoted in capital letters. For example, T is the usual designation for rotation matrices (it certainly depends on how you rotate the system or camera). Then formula (11) goes into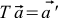 .
.
Matrices have an identity matrix — in the sense that any vector, being multiplied by it on the left, remains itself. And any matrix too. The identity matrix looks like a table, all filled with zeros, only on the diagonal are units. Such a matrix corresponds to a rotation of zero degrees. That is the lack of rotation. She looks like this:
(13)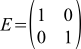
If you count or think a little, then multiplying the rotation matrices corresponds to several turns made one after another (but in a different order, from right to left). So if your program has several previously known turns in a row, then do not rush to apply them to all points in your three-dimensional world. Better multiply the matrices, get a common rotation matrix, and apply it already.
For many matrices, one can find such that when the first is multiplied by the second, the identity matrix is obtained. These new matrices are called inverse, and for T they are denoted as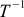 . That is
. That is 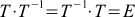 .
.
If you think a little more, then such a matrix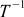 should correspond to the rotation opposite for T — such that neutralizes T. This is already very convenient. If you learn how to calculate inverse matrices, you can easily rotate the camera back, if necessary.
should correspond to the rotation opposite for T — such that neutralizes T. This is already very convenient. If you learn how to calculate inverse matrices, you can easily rotate the camera back, if necessary.
If you think a little bit, and even a little count, then for the rotation matrices, due to the fact that they have a special structure (see formula (10)), it is very easy to obtain inverse matrices: it is enough to simply rotate the matrix along the diagonal from the upper left to bottom right corner (of the same diagonal along which there are units in the identity matrix). This operation is called transposition . It is much (much, much) faster than the search for the inverse matrix in the general case.
Finally, let's move on to three-dimensional space. All formulas are transformed trivially — three coordinates appear in the vectors, three sums appear in the scalar product, etc.
Complexity arises only with the rotation matrix. It is almost intuitively obvious that any rotation can be represented as a sequence of three turns (along OX, OY, OZ) (however, you need to work a little to show it) —so you can set any rotation with these three rotation angles. Three matrices corresponding to these rotations can be multiplied, and get a common matrix for any three-dimensional rotation (with three parameters — rotation angles relative to the coordinate axes). Her appearance can be found on Wikipedia .
It can be shown that instead of three angles, any three-dimensional rotation can be defined by the vector around which the rotation takes place, and by the angle at which we rotate the camera along this vector (we put it counterclockwise if we look from the end of the vector). Oddly enough (or rather, of course), this method also requires three numbers. Since the length of the vector is not important to us, we can make it a unit length. Then, to set it, we need only two numbers (for example, two angles — say, relative to OX and OY). To these two numbers is added the angle by which we will rotate relative to the vector. The formula for the rotation matrix with these parameters can also be found on Wikipedia .
That's all, thanks for your attention.
PS In the process of preparing the article, it turned out that the formulas look a bit blurry, although they seem to have been saved from 600 dpi in png. Apparently, this is so unfortunate Inkscape saves small png. I wildly apologize for this, but I have no strength to redo it.
PPS Although the pictures are uploaded to habrastorage, but sometimes some are not displayed. Apparently some problems with habrastorage. Try just reload the page
Introduction
Task. Suppose we have a two-dimensional picture, as below (house).

Suppose also that we look at the house from the origin in the direction of OX. Now we have turned a certain angle counterclockwise. Question: what will the house look like for us? Intuitively, the result will be approximately the same as in the picture below.

But how to calculate the result? And, worst of all, how to do it in three-dimensional space? If, for example, we rotate the camera very cunningly: first along the OZ axis, then OX, then OY?
The answers to these questions will be given in the article below. First, I will tell you how to represent the house in the form of numbers (that is, I will talk about vectors), then about what angles between vectors (that is, about a scalar product) are, and finally, how to rotate the camera (about the rotation matrix).
Vector coordinates
Let's think about vectors. That is, about arrows with length and direction.

Applied to computer graphics — each such arrow defines a point in space.

We also want to learn to rotate them. Because when we turn all the arrows in the picture above, we turn the house. Let's imagine that all we can do with these arrows is add and multiply by a number. Like in school: to add two vectors, you need to draw a line from the beginning of the first vector to the end of the second.

For now, we will focus on two-dimensional vectors. To begin with, we would like to learn how to write down these vectors somehow through numbers, because every time drawing them on paper in the form of arrows is not very convenient.
We learn how to do this, remembering that any vector can be represented as the sum of some special vectors (OX and OY), possibly multiplied by certain coefficients. These special vectors are called basic, and the coefficients are nothing more than the coordinates of our vector. If we denote the basis vectors by
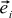 (here, i is the index of the vector, it is either 1 or 2), the vector in question is considered as
(here, i is the index of the vector, it is either 1 or 2), the vector in question is considered as 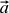 , and the coordinates of the latter as
, and the coordinates of the latter as 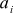 , then we obtain the formula
, then we obtain the formula (1)
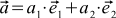
It can be shown that these coordinates will be unique for this basis .

The benefits of assigning coordinates to our arrows are obvious — before, you had to constantly draw an arrow to describe a vector, and now you just need to write two numbers — the coordinates of this vector. For example, we can agree to write something like this:
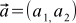 . Or this:
. Or this: 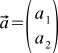 . Then
. Then 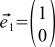 , a
, a  . Wonderful.
. Wonderful. In real math, the procedure is slightly different. First, we describe the properties that any objects must satisfy, so that we call them vectors. They are very natural. For example, vectors must support the addition (two vectors) and multiplication by a number operation. The sum of two vectors should not depend on the order of the terms. The sum of the three vectors should not depend on the order in which we add them in pairs. And so on. The full list is on Wikipedia..
If our pieces of any kind satisfy these properties, then these pieces can be called vectors (this is duck typing). And the whole set of these pieces is a vector or linear space. The properties above are called axioms, and from them all other properties of vectors (or linear space) are deduced — hence the name “ linear algebra"). For example, it can be deduced that among the vectors there will exist such special basis vectors through which any vector can be expressed by formula (1) and that this expansion into coordinates will be unique for this basis. You can quickly show that our arrows just satisfy these axioms. The axiomatic approach is convenient, because if we come across some other objects that satisfy the axioms, then we can immediately apply all the results of our theory to them. In addition, this way we avoid the definitions of arrows on the fingers at the beginning of the theory.
It can be easily shown (from the very axioms) that when the vectors are added, their corresponding coordinates will be added, and when the vector is multiplied by a number, all coordinates are multiplied by the same number. Now, to add two vectors, as in the picture below, we can not draw them (and does not lead the line from the start of the first vector to the end of the second), and to write, for example
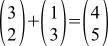 .
.
Scalar product
Let's now introduce a special function of two arbitrary vectors a and b, which we will call the scalar product. We shall denote it like this:
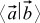 . These trendy brackets are scientifically called bra and ket vectors . There is no benefit from them yet, but it looks great — in addition, this notation still has a deep meaning, especially if you go into mathematical details or quantum mechanics.
. These trendy brackets are scientifically called bra and ket vectors . There is no benefit from them yet, but it looks great — in addition, this notation still has a deep meaning, especially if you go into mathematical details or quantum mechanics. In the spirit of our axiomatic approach, we only require that the scalar product satisfy several axioms . If instead of the first vector we take the sum of vectors of the type
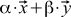 , then we want
, then we want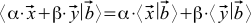 . Here, Greek letters are factors, x and y are vectors. We also want that if we substitute such a sum instead of the second vector, then we can make the same transformations (the scalar product of the sum of vectors also turns out to be the sum of scalar products, and the factors are also taken out of brackets). In addition, we want the values to
. Here, Greek letters are factors, x and y are vectors. We also want that if we substitute such a sum instead of the second vector, then we can make the same transformations (the scalar product of the sum of vectors also turns out to be the sum of scalar products, and the factors are also taken out of brackets). In addition, we want the values to 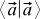 always be non-negative. Finally, we want it to be
always be non-negative. Finally, we want it to be 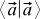 zero if and only if the vector itself is
zero if and only if the vector itself is 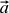 zero. Oh yes, and more so
zero. Oh yes, and more so 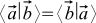 .
. If we add a ruler and a protractor to our arrows on paper, then the function known from school will satisfy these axioms:
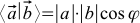 where the lengths of the vectors are measured by a ruler, the angle between the vectors is a
where the lengths of the vectors are measured by a ruler, the angle between the vectors is a 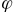 protractor.
protractor.If the ruler and protractor we do not, then the scalar product can be defined length vektora-
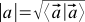 s angle between the vectors
s angle between the vectors 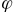 :
: 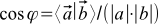 . Of course, the angle depends on the method of determining the scalar product.
. Of course, the angle depends on the method of determining the scalar product. Let's see how the scalar product is expressed through the individual coordinates of the vectors. Suppose we have two vectors a and b that look like this:
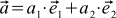 ,
,  . Then
. Then  .
. It doesn’t look very good. To make life better, we will continue to work only with special coordinate systems. We will choose only those coordinate systems in which the basis vectors have unit length and are perpendicular to each other. In other words,
(2a)
 if
if 
(2b)
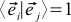 if
if 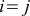
Such vectors are called orthonormal. The expression for the scalar product in orthonormal coordinate systems is transformed beyond recognition:
(3)
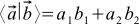
All coordinate systems in this article are assumed to be orthonormal. Surprisingly, it follows from our construction that the result of formula (3) does not depend on which orthonormal basis for coordinates to choose.
By carefully looking at the picture “Decomposition of the vector into coordinates” (it is given again after this paragraph), one can suspect that the coordinate of the vector is nothing more than its projection onto the corresponding base vector. That is, the value of the scalar product of the original vector with one of the basis vectors:
(4)
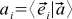

Indeed, for example,
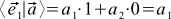 . This seems to be a tautology, because the coordinates of the basis vectors in their own basis will always be (1, 0) and (0, 1). But we can take other basis vectors, and express them through the old basis. For example, a new orthonormal basis may look like in the old basis
. This seems to be a tautology, because the coordinates of the basis vectors in their own basis will always be (1, 0) and (0, 1). But we can take other basis vectors, and express them through the old basis. For example, a new orthonormal basis may look like in the old basis 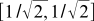 and
and 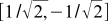 . And then we can determine, for example, the first coordinate of the vector
. And then we can determine, for example, the first coordinate of the vector 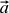 in the new basis by the formula (4) as
in the new basis by the formula (4) as 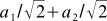 .
.A meticulous reader will say "but formula (3) can be used as a definition of a scalar product, and then we do not need any orthonormalization of basis vectors." And it will be right that formula (3) can work as one of the definitions of a scalar product. But there is a subtle point: then we need to show that when the coordinate system changes, the same formula, but with the coordinates of the vectors a and b from another basis, will give the same number. And this will be only if all the bases are orthonormal. This can be shown by reading the next section.
Coordinate system rotation
Let's find out how the coordinates of the vectors change if we change the entire coordinate system. Why do we even need to change the coordinate system? If you think a little, it will become clear that the rotation of the coordinate system is equivalent to the rotation of the camera in 3D or 2D modeling (see a slightly modified picture with a house below). So learning how to rotate a coordinate system is just what we need.

Let's denote the i-th coordinate of the vector a in the new coordinate system as
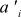 , and the new basis vectors as
, and the new basis vectors as 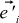 . In addition, we denote the jth coordinate of the OLD basis vector i in the NEW basis as
. In addition, we denote the jth coordinate of the OLD basis vector i in the NEW basis as 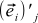 . Finally, we denote the ith coordinate of the NEW basis vector j in the OLD basis as
. Finally, we denote the ith coordinate of the NEW basis vector j in the OLD basis as . Now we can express the original vector and the old basis vectors through the new basis vectors. Namely,
. Now we can express the original vector and the old basis vectors through the new basis vectors. Namely, (5)
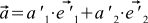 and
and (6)
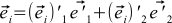
In addition, new basic vectors can be expressed in terms of the old ones:
(7)
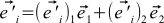
Some of these expansions are shown in the picture below.

Now we simply rewrite formula (1) through the vectors of the new basis:
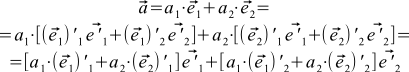
If we compare this with formula (5), and recall that the coordinates of the vectors are uniquely determined, we can see that
(8)
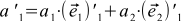 and it is
and it is 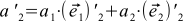
amazing how these formulas look like equations (3 )! They look like a scalar product of a vector
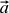 with certain vectors (we will show below that this is not accidental).
with certain vectors (we will show below that this is not accidental). If we write equations (9) with one formula, we get
(9)
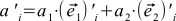
can derive this formula differently combining (4), (1) and (7)
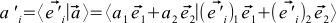 . If we recall the properties of the scalar product, then this formula splits into four sums. If now we recall that our basis vectors are orthonormal, we obtain
. If we recall the properties of the scalar product, then this formula splits into four sums. If now we recall that our basis vectors are orthonormal, we obtain 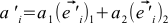 .
. This formula does not look exactly like formula (9):
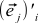 they stand instead
they stand instead 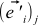 . This is not a mistake — simple
. This is not a mistake — simple 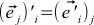 . Ie j Star OLD coordinate basis vector i in the new basis
. Ie j Star OLD coordinate basis vector i in the new basis 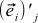 is always equal to the i -th coordinates of the new basis vector j in the old basis,
is always equal to the i -th coordinates of the new basis vector j in the old basis, 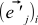 . This will become obvious if you try to express these coordinates through the formula (4):
. This will become obvious if you try to express these coordinates through the formula (4): (10)
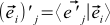 ,
,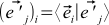
And the scalar product, as we recall, does not depend on the order of the product of vectors.
This will become even more obvious if we recall that these scalar products are the angles between different (unit) basis vectors. These angles, of course, are independent of whether to set them aside clockwise or counterclockwise.
Rotation matrix
If you are familiar with matrices, then formula (9) (two formulas) can be rewritten in matrix form
(11)
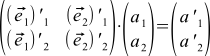
What does this all mean ?! As usual, there is no magic here — we just agree that the multiplication of this plate from the numbers on the left to the vector on the right is calculated as formula (9). That is, we multiply each row of the label by a column to the right (as if we are doing the scalar product of two vectors), and write the results under each other, also getting a column.
By the way, we can extend this rule to the multiplication of two labels: we agree to multiply each row of the first label by each column of the second, and also write the results in the label: we multiply the first row with the third column in the first row and third column. Formula (11) then becomes a special case of this rule. Schematically, this is all depicted in the figure below.
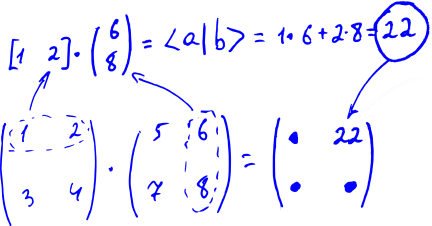
The tablets of numbers equipped with this rule of multiplication by vectors and other tablets will be called matrices.
The rule of matrix multiplication looks even more natural if we learn that the scalar product, as we agreed to denote it
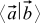 , in fact assumes that the vector a is a string, and the vector b-column. Before that, we agreed to write vectors in columns, and the row vector a is actually not just an inverted vector a , but an object of a special dual vector space . But in the case of orthonormal bases, the coordinates of the original and dual vectors coincide (that is, the a-row and a-column are the same), so these details do not affect our presentation. Everything is fine. In addition, on the other hand, formula (3) for the scalar product is a special case of matrix multiplication.
, in fact assumes that the vector a is a string, and the vector b-column. Before that, we agreed to write vectors in columns, and the row vector a is actually not just an inverted vector a , but an object of a special dual vector space . But in the case of orthonormal bases, the coordinates of the original and dual vectors coincide (that is, the a-row and a-column are the same), so these details do not affect our presentation. Everything is fine. In addition, on the other hand, formula (3) for the scalar product is a special case of matrix multiplication. In general, it can be shown that multiplication by matrices corresponds to certain transformations of vectors. Instead of "transformation" it is customary to say operators. And matrix multiplication is a linear operator. In addition, for any linear operator, there is one and only one operator matrix. You can read about what it is on Wikipedia . If you describe it here, then the article will never end.
So, as we found out, the rotation of the coordinate system is equivalent to the rotation of the camera in 3D or 2D modeling. Therefore, the matrix from formula (11) is called the rotation matrix. Formula (11) can be interpreted not as a replacement of the coordinate system, but as a description of the rotation operator.
It is not yet clear how to calculate this matrix. This is not difficult if we turn to formulas (10) and recall that the cosine of the angle between unit vectors is equal to their scalar product. Then, for example
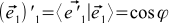 , where
, where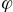 —The angle of rotation of the coordinate system (camera). It is, by definition, positive if the rotation is counterclockwise, and negative if it is rotated clockwise (see the figure below — it was already there, but now it is relevant again). If you tinker a bit with geometry or trigonometry, you can find out that the entire rotation matrix looks like this:
—The angle of rotation of the coordinate system (camera). It is, by definition, positive if the rotation is counterclockwise, and negative if it is rotated clockwise (see the figure below — it was already there, but now it is relevant again). If you tinker a bit with geometry or trigonometry, you can find out that the entire rotation matrix looks like this: (12a)
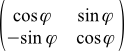
If you look at Wikipedia , the formula there looks a little different:
(12b)
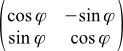
This is all because
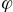 in it is the angle of rotation of the vectors themselves (or our objects such as a house). It is also considered positive if the rotation occurs counterclockwise. But the rotation of the camera is opposite to the rotation of objects, that is, the angle of rotation of the camera is equal to the angle of rotation of the objects, but taken with the opposite sign.
in it is the angle of rotation of the vectors themselves (or our objects such as a house). It is also considered positive if the rotation occurs counterclockwise. But the rotation of the camera is opposite to the rotation of objects, that is, the angle of rotation of the camera is equal to the angle of rotation of the objects, but taken with the opposite sign. Again current drawing:

Pleasant trifles
These matrices are very convenient things. They can be multiplied and added, moreover, not only two, but three and four. Matrices can be denoted in capital letters. For example, T is the usual designation for rotation matrices (it certainly depends on how you rotate the system or camera). Then formula (11) goes into
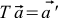 .
. Matrices have an identity matrix — in the sense that any vector, being multiplied by it on the left, remains itself. And any matrix too. The identity matrix looks like a table, all filled with zeros, only on the diagonal are units. Such a matrix corresponds to a rotation of zero degrees. That is the lack of rotation. She looks like this:
(13)
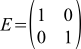
If you count or think a little, then multiplying the rotation matrices corresponds to several turns made one after another (but in a different order, from right to left). So if your program has several previously known turns in a row, then do not rush to apply them to all points in your three-dimensional world. Better multiply the matrices, get a common rotation matrix, and apply it already.
For many matrices, one can find such that when the first is multiplied by the second, the identity matrix is obtained. These new matrices are called inverse, and for T they are denoted as
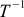 . That is
. That is 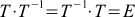 .
. If you think a little more, then such a matrix
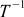 should correspond to the rotation opposite for T — such that neutralizes T. This is already very convenient. If you learn how to calculate inverse matrices, you can easily rotate the camera back, if necessary.
should correspond to the rotation opposite for T — such that neutralizes T. This is already very convenient. If you learn how to calculate inverse matrices, you can easily rotate the camera back, if necessary. If you think a little bit, and even a little count, then for the rotation matrices, due to the fact that they have a special structure (see formula (10)), it is very easy to obtain inverse matrices: it is enough to simply rotate the matrix along the diagonal from the upper left to bottom right corner (of the same diagonal along which there are units in the identity matrix). This operation is called transposition . It is much (much, much) faster than the search for the inverse matrix in the general case.
Three-dimensional space
Finally, let's move on to three-dimensional space. All formulas are transformed trivially — three coordinates appear in the vectors, three sums appear in the scalar product, etc.
Complexity arises only with the rotation matrix. It is almost intuitively obvious that any rotation can be represented as a sequence of three turns (along OX, OY, OZ) (however, you need to work a little to show it) —so you can set any rotation with these three rotation angles. Three matrices corresponding to these rotations can be multiplied, and get a common matrix for any three-dimensional rotation (with three parameters — rotation angles relative to the coordinate axes). Her appearance can be found on Wikipedia .
It can be shown that instead of three angles, any three-dimensional rotation can be defined by the vector around which the rotation takes place, and by the angle at which we rotate the camera along this vector (we put it counterclockwise if we look from the end of the vector). Oddly enough (or rather, of course), this method also requires three numbers. Since the length of the vector is not important to us, we can make it a unit length. Then, to set it, we need only two numbers (for example, two angles — say, relative to OX and OY). To these two numbers is added the angle by which we will rotate relative to the vector. The formula for the rotation matrix with these parameters can also be found on Wikipedia .
That's all, thanks for your attention.
PS In the process of preparing the article, it turned out that the formulas look a bit blurry, although they seem to have been saved from 600 dpi in png. Apparently, this is so unfortunate Inkscape saves small png. I wildly apologize for this, but I have no strength to redo it.
PPS Although the pictures are uploaded to habrastorage, but sometimes some are not displayed. Apparently some problems with habrastorage. Try just reload the page
