The task of “Reliability of logic circuits”
Combinational logic circuits are part of all modern processors and other electronic information processing tools. Processors are used universally and are becoming increasingly complex. The number of transistors in a modern processor has already exceeded 2 billion? And it seems that growth does not plan to stop. At the same time, the technological processes of the production of processors are reduced. Transistors are becoming smaller and more vulnerable to external influences. And now, not even the strongest external radiation and magnetic fields can lead to short-term changes in logical values in microelectronic circuits. This problem is especially relevant in space and other critical systems for reliability. In this problem, we pose the question: how, knowing the logical purpose of the circuit, make it more resistant to external influences? Your task will be to develop an algorithm for creating such a stable scheme.
Let a logic diagram be given, without feedback, consisting of the following 6 elements:
| Title | Description | Operation | Picture |
|---|---|---|---|
| INV | inverter | OUT =! A |  |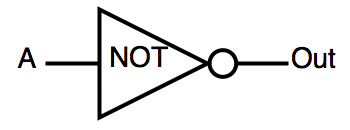
| AND | logical "AND" | OUT = A & B |  |
| OR | logical "OR" | OUT = A | B |  |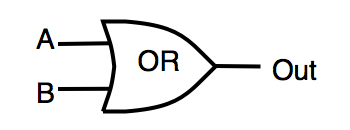
| Nand | inverted AND | OUT =! (A&B) |  |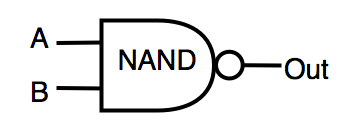
| Nor | inverted OR | OUT =! (A | B) |  |
| Xor | exclusive "OR" | OUT = A ^ B |  |
The circuit is affected by environmental noise, with some probability changing the logical value of the valves to the opposite. It is necessary to construct a circuit that performs the same logical function as the original, but is less prone to failures. According to the conditions of the problem, the circuit that you designed should be no more than “ K ” times larger than the original in area.
One of the parameters that characterize the stability of logic circuits to failures is COF - "General error tolerance of the circuit." COF is calculated as the ratio of the number of correct results of the circuit (all outputs of the circuit must have the correct value) to the total number of tests performed. Accordingly, for the most reliable schemes, COF tends to 1.
Each logical gate of the circuit is characterized by the following parameters: S is the area of the gate, p is the probability of failure in percent under current external conditions.
Input data
The first line shows the number Z - the number of tests ( Z <400). Followed by Z tests.
The first line of each test shows the number K (2.0 ≤ K ≤ 20.0) - the maximum redundancy of the circuit over the area.
The next 6 lines indicate two numbers, the area S (1 ≤ S ≤ 100) and the probability of failure q (0 ≤ q ≤ 20) in percent, the parameters of each of the logical elements in the following order: INV, AND, OR, NAND, NOR, XOR.
The next line shows the number “ I ” (0 < I <250) - the number of inputs of the circuit, followed by I lines of no more than 20 characters in each separated by spaces - the names of the input nodes of the circuit.
The next line shows the number “ O ” (0 < O <150) - the number of circuit outputs, then O lines of no more than 20 characters in each separated by spaces - the names of the output nodes of the circuit.
The following is the number of logic gates in the N circuit (1 < N <5000), followed by N lines with a description of each gate.
The description of each gate begins with its type, followed by the names of the input nodes, then the name of the output node
Output
For each test, you must display a description of the circuit in the following format. On the first line, the number N (1 < N <100000) is the number of valves in the resulting circuit. This is followed by N - lines with descriptions of valves. The description of each gate begins with its type, followed by the names of the input nodes, followed by the name of the output node.
Scoring Points
The number of points earned by Score is summarized in all tests. The number of points received for the test will be equal to the COF value calculated for your scheme. Is COF calculated using the Monte Carlo method ? in two stages:
1) at the first stage, the judge program determines that your circuit works identically to the original. The same test sequences (several thousand times) are input to both circuits and the logical values at the circuit outputs are compared. If the logical values are different, then you will receive the status of Wrong Answer.
2) at the second stage, the judge program will randomly invert the values on the valves of your circuit according to the given probabilities and compare the values on your circuit and on the standard circuit. If at least one of the outputs is different, the counter of "incorrect answers" will increase. For the calculation, the formula is used: COF = ( TT - INC ) / TT , where:
TT - the number of tests with at least one embedded error
INC - the number of tests where an error occurred at least on one output of the circuit
The judge program also checks that the redundancy of the circuit does not exceed the specified one.
Solution Limitations
- The program size is not more than 50 KB
- Time to complete no more than 50 seconds
- More than 40 programming languages are supported (C / C ++, Java, Pascal, etc.)
Example
Input data:
Let the following logic be given (see the figure). The required redundancy should not be more than 4.1 times. The scheme is built on a library in which:
INV has an area of 50 and a 3% failure probability
AND has an area of 60 and a failure probability of 3.1%
OR has an area of 60 and a failure probability of 3.2%
NAND has an area of 70 and a 3.3% chance of failure
NOR has an area of 70 and a failure probability of 3.4%
XOR has an area of 70 and a failure rate of 3.5%
The input file for this task will look like this:
1 5.1 50.0 3.0 60.0 3.1 60.0 3.2 70.0 3.3 70.0 3.4 70.0 3.5 2 ab 2 cs cc 5 INV a n1 INV b n2 Nand ab cc NAND n1 n2 n3 NAND n3 cc cs
Output:
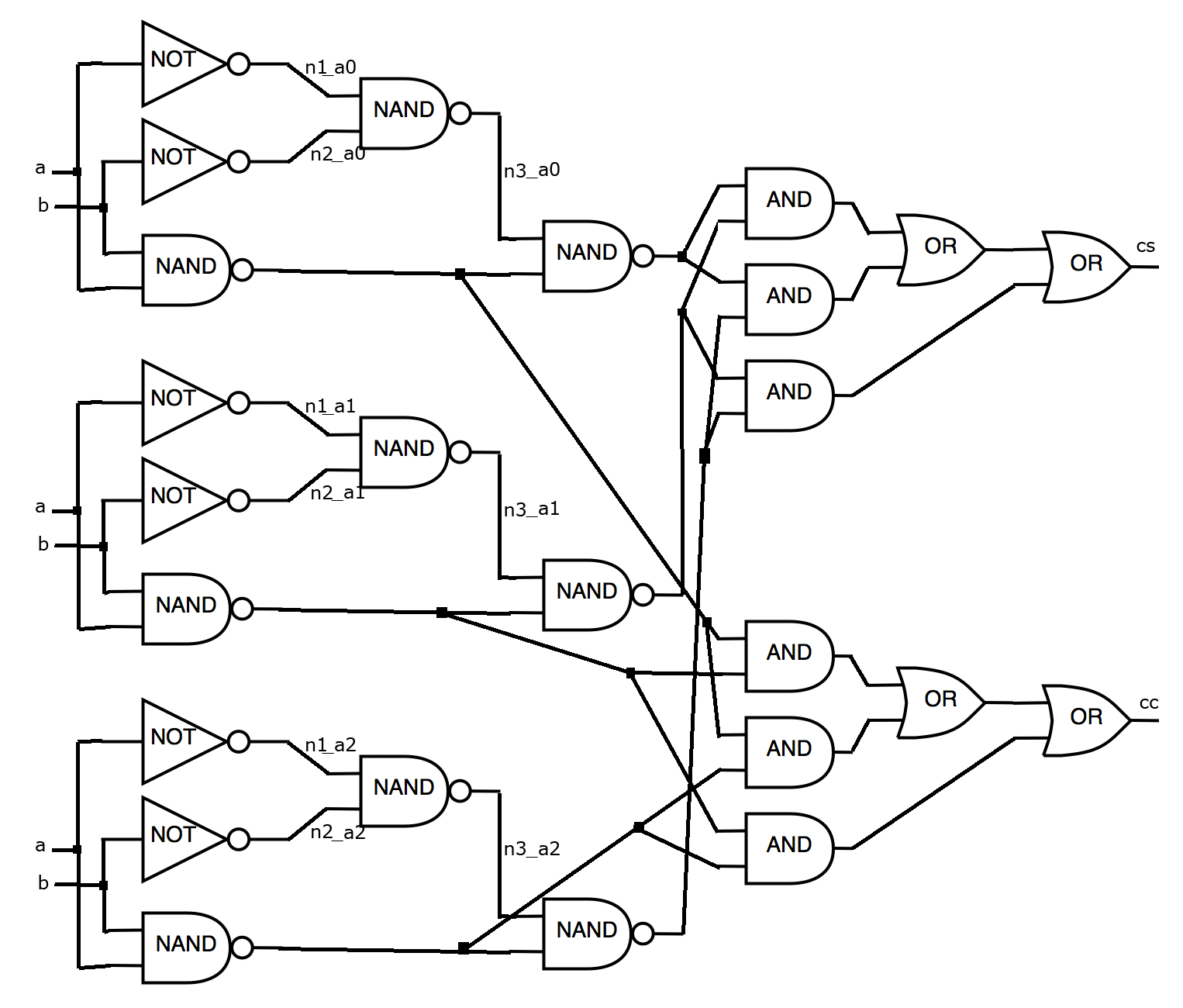
Let our algorithm use the standard technique of tripling and choosing a logical value that is used on more outputs (Triple Modular Redundancy (TMR)) ? . In this case, the output file can be written as follows:
25 INV a n1_a0 INV a n1_a1 INV a n1_a2 INV b n2_a0 INV b n2_a1 INV b n2_a2 NAND ab cc_a0 NAND ab cc_a1 NAND ab cc_a2 NAND n1_a0 n2_a0 n3_a0 NAND n1_a1 n2_a1 n3_a1 NAND n1_a2 n2_a2 n3_a2 NAND n3_a0 cc_a0 cs_a0 NAND n3_a1 cc_a1 cs_a1 NAND n3_a2 cc_a2 cs_a2 AND cs_a0 cs_a1 cs_3_0_and_0_out AND cs_a0 cs_a2 cs_5_0_and_0_out AND cs_a1 cs_a2 cs_6_0_and_0_out OR cs_3_0_and_0_out cs_5_0_and_0_out cs_0_or_0_out OR cs_0_or_0_out cs_6_0_and_0_out cs AND cc_a0 cc_a1 cc_3_0_and_0_out AND cc_a0 cc_a2 cc_5_0_and_0_out AND cc_a1 cc_a2 cc_6_0_and_0_out OR cc_3_0_and_0_out cc_5_0_and_0_out cc_0_or_0_out OR cc_0_or_0_out cc_6_0_and_0_out cc
Image for output file
Scoring:
For this decision, after simulation, 0.682661 points will be awarded.
Submitting Solutions
Submit decision * | Sent Solutions Tape | Best solutions |
* - to send, you need an account in the SPOJ (Shere Online Judge) system [ Registration ].
Useful materials
In order not to write programs from scratch, you can use ready-made developments:
1) A simple solution to the problem in C \ C ++ - the program reads the data and displays the circuit as is, without changes.
2) Judge on C \ C ++ - a program that is used on the server to evaluate the solution to the problem. You can use it locally to test the effectiveness of your solutions
3) Test data set - a set of 102 test circuits similar to a closed set on the server.
Authors : Soloviev R.A., Telpukhov D.V.