Cluster analysis (on the example of consumer segmentation) part 1
- Transfer
- Tutorial
We know that the Earth is one of 8 planets that revolve around the Sun. The sun is just a star among about 200 billion stars in the Milky Way galaxy. It is very difficult to realize this number. Knowing this, one can make an assumption about the number of stars in the universe - approximately 4X10 ^ 22. We can see about a million stars in the sky, although this is only a small part of the total actual number of stars. So, we had two questions:

A galaxy is a cluster of stars, gas, dust, planets and interstellar clouds. Typically, galaxies resemble a spiral or edeptic figure. In space, galaxies are separated from each other. Huge black holes are most often the centers of most galaxies.
As we will discuss in the next section, there is much in common between galaxies and cluster analysis. Galaxies exist in three-dimensional space, cluster analysis is a multidimensional analysis conducted in n-dimensional space.
Note: A black hole is the center of the galaxy. We will use a similar idea regarding centroids for cluster analysis.
Suppose you are the head of marketing and consumer relations at a telecommunications company. You understand that all consumers are different, and that you need different strategies to attract different consumers. You’ll appreciate the power of a tool like customer segmentation to optimize costs. In order to refresh your knowledge of cluster analysis, consider the following example, illustrating 8 consumers and the average duration of their conversations (local and international). Below is the data:

For better perception, we will draw a graph where the average duration of international calls and the average duration of local calls will be plotted along the x-axis. Below is the graph:

Note:This is similar to an analysis of the location of stars in the night sky (here the stars are replaced by consumers). In addition, instead of three-dimensional space, we have two-dimensional space defined by the duration of local and international calls, as the x and y axes.
Now, speaking in terms of galaxies, the problem is formulated as follows - to find the position of black holes; in cluster analysis, they are called centroids. To detect centroids, we start by taking arbitrary points as the position of the centroids.
In our case, we place two centroids (C1 and C2) arbitrarily at points with coordinates (1, 1) and (3, 4). Why did we choose these two centroids? The visual display of points on the graph shows us that there are two clusters that we will analyze. However, later we will see that the answer to this question will not be so simple for a large data set.
Next, we will measure the distance between the centroids (C1 and C2) and all the points on the graph using the Euclidean formula to find the distance between two points.
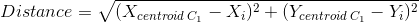
Note: The distance can be calculated using other formulas, for example,
Column 3 and 4 (Distance from C1 and C2) is the distance calculated by this formula. For example, for the first consumer

, Centroid affiliation (last column) is calculated by the principle of proximity to centroids (C1 and C2). The first consumer is closer to centroid No. 1 (1.41 compared to 2.24); therefore, it belongs to the cluster with the centroid C1.

Below is a graph illustrating the centroids C1 and C2 (depicted as blue and orange diamonds). Consumers are depicted in the color of the corresponding centroid to the cluster of which they were assigned.

Since we arbitrarily chose centroids, the second step is to make this choice iterative. The new position of the centroids is selected as the average for the points of the corresponding cluster. So, for example, for the first centroid (these are consumers 1, 2 and 3). Therefore, the new x coordinate for the centroid C1 is the average x coordinate of these consumers (2 + 1 + 1) / 3 = 1.33. We will get new coordinates for C1 (1.33, 2.33) and C2 (4.4, 4.2). The new graph is below:

In the end, we will put the centroids in the center of the corresponding cluster. The chart below:

The positions of our black holes (cluster centers) in our example are C1 (1.75, 2.25) and C2 (4.75, 4.75). The two clusters above are similar to two galaxies separated in space from each other.
So, we will consider examples further. Let us face the challenge of segmenting consumers in two ways: age and income. Suppose we have 2 consumers with an age of 37 and 44 years and an income of $ 90,000 and $ 62,000 respectively. If we want to measure the Euclidean distance between the points (37, 90,000) and (44, 62000), we will see that in this case the variable income “dominates” the variable age and its change strongly affects the distance. We need some strategy to solve this problem, otherwise our analysis will give the wrong result. The solution to this problem is to bring our values to comparable scales. Normalization is the solution to our problem.
There are many approaches to normalizing data. For example, the normalization of the minimum-maximum. For this normalization, the following formula is used

in this case X * is the normalized value, min and max are the minimum and maximum coordinates for the entire set X
(Note, this formula has all the coordinates on the interval [0; 1])
Consider our example, let the maximum revenue is $ 130,000 and the minimum is $ 45,000. The normalized value of income for consumer A is equal.

We will do this exercise for all points for each variable (coordinate). The income for the second consumer (62000) will be 0.2 after the normalization procedure. Additionally, let the minimum and maximum ages be 23 and 58, respectively. After normalization, the ages of our two consumers will be 0.4 and 0.6.
It is easy to see that now all of our data is located between the values 0 and 1. Therefore, we now have normalized data sets in comparable scales.
Remember, before the cluster analysis procedure, you need to normalize.
Article found kuznetsovin
- What is a galaxy?
- And what is the relationship between galaxies and the topic of the article (cluster analysis)

A galaxy is a cluster of stars, gas, dust, planets and interstellar clouds. Typically, galaxies resemble a spiral or edeptic figure. In space, galaxies are separated from each other. Huge black holes are most often the centers of most galaxies.
As we will discuss in the next section, there is much in common between galaxies and cluster analysis. Galaxies exist in three-dimensional space, cluster analysis is a multidimensional analysis conducted in n-dimensional space.
Note: A black hole is the center of the galaxy. We will use a similar idea regarding centroids for cluster analysis.
Cluster analysis
Suppose you are the head of marketing and consumer relations at a telecommunications company. You understand that all consumers are different, and that you need different strategies to attract different consumers. You’ll appreciate the power of a tool like customer segmentation to optimize costs. In order to refresh your knowledge of cluster analysis, consider the following example, illustrating 8 consumers and the average duration of their conversations (local and international). Below is the data:

For better perception, we will draw a graph where the average duration of international calls and the average duration of local calls will be plotted along the x-axis. Below is the graph:

Note:This is similar to an analysis of the location of stars in the night sky (here the stars are replaced by consumers). In addition, instead of three-dimensional space, we have two-dimensional space defined by the duration of local and international calls, as the x and y axes.
Now, speaking in terms of galaxies, the problem is formulated as follows - to find the position of black holes; in cluster analysis, they are called centroids. To detect centroids, we start by taking arbitrary points as the position of the centroids.
Euclidean distance for finding Centroids for Clusters
In our case, we place two centroids (C1 and C2) arbitrarily at points with coordinates (1, 1) and (3, 4). Why did we choose these two centroids? The visual display of points on the graph shows us that there are two clusters that we will analyze. However, later we will see that the answer to this question will not be so simple for a large data set.
Next, we will measure the distance between the centroids (C1 and C2) and all the points on the graph using the Euclidean formula to find the distance between two points.
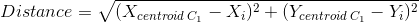
Note: The distance can be calculated using other formulas, for example,
- squared Euclidean distance - to give weight to objects more distant from each other
- Manhattan distance - to reduce emissions
- power distance - to increase / decrease the influence on specific coordinates
- percentage of disagreement - for categorical data
- and etc.
Column 3 and 4 (Distance from C1 and C2) is the distance calculated by this formula. For example, for the first consumer

, Centroid affiliation (last column) is calculated by the principle of proximity to centroids (C1 and C2). The first consumer is closer to centroid No. 1 (1.41 compared to 2.24); therefore, it belongs to the cluster with the centroid C1.

Below is a graph illustrating the centroids C1 and C2 (depicted as blue and orange diamonds). Consumers are depicted in the color of the corresponding centroid to the cluster of which they were assigned.

Since we arbitrarily chose centroids, the second step is to make this choice iterative. The new position of the centroids is selected as the average for the points of the corresponding cluster. So, for example, for the first centroid (these are consumers 1, 2 and 3). Therefore, the new x coordinate for the centroid C1 is the average x coordinate of these consumers (2 + 1 + 1) / 3 = 1.33. We will get new coordinates for C1 (1.33, 2.33) and C2 (4.4, 4.2). The new graph is below:

In the end, we will put the centroids in the center of the corresponding cluster. The chart below:

The positions of our black holes (cluster centers) in our example are C1 (1.75, 2.25) and C2 (4.75, 4.75). The two clusters above are similar to two galaxies separated in space from each other.
So, we will consider examples further. Let us face the challenge of segmenting consumers in two ways: age and income. Suppose we have 2 consumers with an age of 37 and 44 years and an income of $ 90,000 and $ 62,000 respectively. If we want to measure the Euclidean distance between the points (37, 90,000) and (44, 62000), we will see that in this case the variable income “dominates” the variable age and its change strongly affects the distance. We need some strategy to solve this problem, otherwise our analysis will give the wrong result. The solution to this problem is to bring our values to comparable scales. Normalization is the solution to our problem.
Data normalization
There are many approaches to normalizing data. For example, the normalization of the minimum-maximum. For this normalization, the following formula is used

in this case X * is the normalized value, min and max are the minimum and maximum coordinates for the entire set X
(Note, this formula has all the coordinates on the interval [0; 1])
Consider our example, let the maximum revenue is $ 130,000 and the minimum is $ 45,000. The normalized value of income for consumer A is equal.

We will do this exercise for all points for each variable (coordinate). The income for the second consumer (62000) will be 0.2 after the normalization procedure. Additionally, let the minimum and maximum ages be 23 and 58, respectively. After normalization, the ages of our two consumers will be 0.4 and 0.6.
It is easy to see that now all of our data is located between the values 0 and 1. Therefore, we now have normalized data sets in comparable scales.
Remember, before the cluster analysis procedure, you need to normalize.
Article found kuznetsovin
