How to roll dice without OpenGL

One good person wanted to make an e-book for iOS , a collection of aphorisms. Phrases fly out randomly; data is provided in the format of comma separated value . With a flash drive and oral TK, he came to a friend-programmer. The programmer estimated the approximate amount of work

• Convert data to sqlite ;
• We get three UIView (left, right and central);
• In each UIView we add UITextView and UILabel ;
• We process pressing touchesBegin to scroll left and right aphorisms;
• Add a button - show a random aphorism.
• Add bookmarks.
• Get $ 1,000

Work for 2 days, the programmer agreed.
However, in TK there was one more condition - with a random choice of aphorism, a dice should roll on the screen . The most ordinary of six faces.

The programmer did all the work except the cube quickly. Aphorisms popped up like a hell out of a snuffbox, pages flipped like alive. There is a cube left.

How to draw a three-dimensional cube without using OpenGL

In regular games, UIImageView * p uses its own set of functions and fields for

• move to the point (x, y) , for example p.center = CGPoint (x, y) ;
• scaling, for example p.transform = CGAffineTransformMakeScale (sx, sy);
• rotations, for example p.transform = CGAffineTransformMakeRotate (alpha) ;

However, there is direct access to the UIImageView 2D transformation matrix

             UIImageView *p = [dice objectAtIndex:i];
             CGAffineTransform diceTransform = CGAffineTransformMake(a, b, c, d, tx, ty);
             p.transform = diceTransform;

CGAffineTransform two-dimensional transformation matrix has 6 parameters

struct CGAffineTransform {
  CGFloat a, b, c, d;
  CGFloat tx, ty;
};

Any point in the image is converted according to the formula

CGPointApplyAffineTransform(CGPoint point, CGAffineTransform t)
{
  CGPoint p;
  p.x = a * point.x + c * point.y + tx;
  p.y = b * point.x + d * point.y + ty;
  return p;
}

For example, to rotate a picture by an angle angle , the transformation matrix takes the form

   t' = [ cos(angle) sin(angle) -sin(angle) cos(angle) 0 0 ] 

To move a picture-image onto a vector (tx, ty) , the transformation matrix takes the form

  t' = [ 1 0 0 1 tx ty ] 

And so on.

Thus, we can transform an arbitrary triangle into a given triangle by applying a transformation matrix with calculated coefficients to it.

Consider the face of the cube. The square picture must be divided into two triangles. We make empty pixels transparent. We save the images in the dice_1.png and dice_2.png files .


In the project, we create two variables with the specified pictures.

UIImageView *p1 =  [[UIImageView alloc]  initWithImage:[UIImage imageNamed:@"dice_1"] ];
UIImageView *p2 =  [[UIImageView alloc]  initWithImage:[UIImage imageNamed:@"dice_2"] ];

In the process of cube animation, the problem of displaying the face arises, which reduces to the task of displaying two triangles on the screen.

Consider the upper triangle


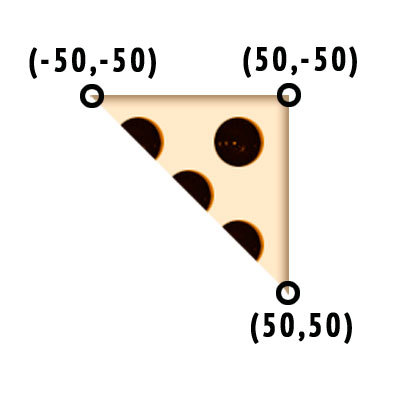
that should be transformed on the screen into a triangle of arbitrary form with vertices at the points (x1, y1), (x2, y2), (x3, y3)


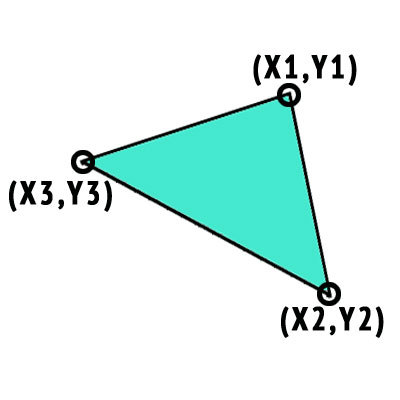
Thus, we have 6 linear equations with 6 unknowns.
As a result of simple transformations, we obtain a solution for 6 unknowns a, b, c, d, tx, ty ;

                float ddt = 1.0/xsize;
                float a = ddt*(x3-x2);
                float b = ddt*(y3-y2);
                float c= ddt*(x2-x1);
                float d= ddt*(y2-y1);
                float tx = 0.5*(x1+x3);
                float ty = 0.5*(y1+y3);

Here xsize is the linear size in pixels of the original image. For example xsize = 100 for a picture of size 100 by 100.
The problem is solved.