Shadow Rendering Using Parallel-Split Shadow Mapping
 Hello, Habr! My previous post on graphics programming was well-received by the community, and I ventured another one. Today I’ll talk about the Parallel-Split Shadow Mapping (PSSM) shadow rendering algorithm that I first encountered when it came to working to display shadows at a great distance from the player. Then I was limited by the set of features of Direct3D 10, now I implemented the algorithm on Direct3D 11 and OpenGL 4.3. The PSSM algorithm is described in more detail in the Gems 3 GPU both from a mathematical point of view and from the point of view of implementation on Direct3D 9 and 10. For details, I ask for cat.
Hello, Habr! My previous post on graphics programming was well-received by the community, and I ventured another one. Today I’ll talk about the Parallel-Split Shadow Mapping (PSSM) shadow rendering algorithm that I first encountered when it came to working to display shadows at a great distance from the player. Then I was limited by the set of features of Direct3D 10, now I implemented the algorithm on Direct3D 11 and OpenGL 4.3. The PSSM algorithm is described in more detail in the Gems 3 GPU both from a mathematical point of view and from the point of view of implementation on Direct3D 9 and 10. For details, I ask for cat.The demo can be found here . The project is called Demo_PSSM. To build, you will need Visual Studio 2012/2013 and CMake .
Shadow mapping
The original shadow mapping algorithm was invented for a long time. The principle of its operation is as follows:
- We draw the scene into the texture (shadow map) from the position of the light source. It is important to note here that for different types of light sources everything happens a little differently.
Directional light sources (such as a certain approximation include sunlight) do not have a position in space, however, you have to choose this position to form a shadow map. Usually it is tied to the position of the observer, so that objects that are directly in the observer's field of vision fall into the shadow map. When rendering, orthographic projection is used .
Projection light sources (lamps with an opaque lampshade, spotlights) have a certain position in space and limit the propagation of light in certain directions. When rendering the shadow map in this case, the usual perspective projection matrix is used .
Omni-directional light sources (an incandescent lamp, for example), although they have a certain position in space, spread light in all directions. In order to correctly construct shadows from such a light source, it is necessary to use cubic textures (cube maps), which, as a rule, means drawing a scene into a shadow map 6 times. Not every game can afford dynamic shadows from such sources of light, and not every game needs it. If you are interested in the working principles of this approach, there areold article on this topic.
In addition, there is a subclass of shadow mapping algorithms ( LiSPSM , TSM , PSM , etc.) that use non-standard projection view matrices to improve the quality of shadows and eliminate the disadvantages of the original approach.
Whatever way the shadow map is formed, it invariably contains the distance from the light source to the nearest visible (from the position of the light source) point or a function of this distance in more complex varieties of the algorithm. - We draw a scene from the main camera. In order to understand whether a point of an object is in the shadow, it is enough to translate the coordinates of this point into the space of the shadow map and make a comparison. The space of the shadow map is determined by the matrix of the projection view, which was used in the formation of this map. Transferring the coordinates of the point of the object into this space and transforming the coordinates from the range [-1; -1] to [0; 1] , we obtain texture coordinates. If the received coordinates are outside the range [0; 1], then this point did not fall into the shadow map, and it can be considered unshaded. Having made a selection from the shadow map based on the obtained texture coordinates, we get the distance between the light source and the point of an object closest to it. If we compare this distance with the distance between the current point and the light source, the point appears in the shadow, if the value in the shadow map is less. This is quite simple from a logical point of view, if the value from the shadow map is less, then at this point there is some kind of object that is closer to the light source, and we are in its shadow.
Shadow mapping is by far the most common algorithm for rendering dynamic shadows. The implementation of one or another modification of the algorithm can be found in almost any graphics engine. The main advantage of this algorithm is that it provides the rapid formation of shadows from arbitrarily geometrically complex objects. However, the existence of a wide range of variations of the algorithm is largely due to its shortcomings, which can lead to very unpleasant graphical artifacts. Problems specific to PPSM and ways to overcome them will be discussed below.
Parallel-Split Shadow Mapping
Consider the following task: it is necessary to draw dynamic shadows from objects located at a considerable distance from the player without affecting the shadows of closely located objects. We restrict ourselves to directed sunlight.
This kind of task can be especially relevant in outdoor games, where in some situations a player can see the landscape hundreds of meters in front of him. In this case, the further we want to see the shadow, the more space should fall into the shadow map. To maintain proper resolution of objects in the shadow map, we are forced to increase the resolution of the map itself, which first leads to a decrease in performance, then we run into a limit on the maximum size of the render target. As a result, balancing between performance and shadow quality, we get shadows with a clearly visible aliasing effect that is poorly masked even by blurring. It is clear that such a solution cannot satisfy us.
To solve this problem, we can come up with a projection matrix such that objects close to the player receive more area in the shadow map than objects that are far away. This is the main idea of the Perspective Shadow Mapping (PSM) algorithm and a number of other algorithms. The main advantage of this approach is the fact that we practically did not change the rendering process of the scene, only the way of calculating the matrix of the view-projection changed. This approach can be easily integrated into an existing game or engine without the need for major modifications to the latter. The main drawback of such approaches is the boundary conditions. Imagine a situation that we draw shadows from the sun at sunset. When the Sun approaches the horizon, objects in the shadow map begin to overlap greatly. In this case, an atypical projection matrix can aggravate the situation. In other words, PSM class algorithms work well in certain situations, for example, when shadows are drawn in the game from the “motionless Sun” close to the zenith.
A fundamentally different approach is proposed in the PSSM algorithm. For some, this algorithm may be known as Cascaded Shadow Mapping (CSM). Formally, these are different algorithms, I would even say that PSSM is a special case of CSM. In this algorithm, it is proposed to divide the pyramid of visibility (frustum) of the main camera into segments. In the case of PSSM - with borders parallel to the near and far clipping planes, in the case of CSM - the type of separation is not strictly regulated. For each segment ( split in the terminology of the algorithm), its own shadow map is built. An example of separation is shown in the figure below.
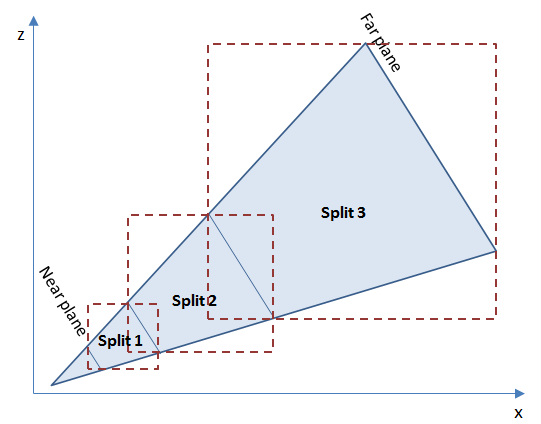
In the figure, you can see the partition of the visibility pyramid into 3 segments. Each of the segments is highlighted by a bounding box (in three-dimensional space there will be a box, bounding box). For each of these limited parts of the space will be built its own shadow map. An attentive reader will note that here I used bounding parallelepipeds aligned on axes. Unbalanced can also be used, this will add additional complexity to the object clipping algorithm and will slightly change the way the view matrix is formed from the position of the light source. As the pyramid of visibility expands, the area of segments closer to the camera can be significantly less than the area of the farthest. With the same resolution of shadow maps, this means a higher resolution for the shadow from closely located objects. In the aboveThe article in the GPU Gems 3 proposed the following scheme for calculating the partition distances of the visibility pyramid:
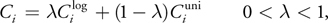
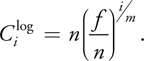
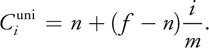
where i is the partition index, m is the number of partitions, n is the distance to the near clipping plane, f is the distance to the far clipping plane, and λ is the coefficient that determines the interpolation between the logarithmic and a uniform partition scale.
General in implementation
The PSSM algorithm in the implementation on Direct3D 11 and OpenGL has much in common. To implement the algorithm, you must prepare the following:
- Several shadow cards (according to the number of partitions). At first glance, it seems that to get several shadow maps, you need to draw objects several times. Actually, it is not necessary to do this explicitly, we will use the mechanism of hardware instancing. To do this, we need a so-called array of textures for rendering and a simple geometric shader.
- The mechanism of clipping objects. The objects of the game world can be of different geometric shapes and have different positions in space. Extended objects can be seen in several shadow maps, small objects in only one. An object can appear directly on the border of neighboring segments and must be drawn in at least 2 shadow maps. Thus, a mechanism is needed to determine which subset of shadow maps an object falls into.
- Mechanism for determining the optimal number of partitions. Rendering shadow maps for each segment per frame can be a waste of computing resources. In many situations, the player sees in front of him only a small section of the game world (for example, he looks under his feet, or his gaze rested on the wall in front of him). It is clear that this greatly depends on the type of review in the game, but it would be nice to have such an optimization.
As a result, we obtain the following algorithm for the formation of projection-type matrices for rendering shadow maps:
- Calculate the distances for breaking the pyramid of visibility for the worst case. The worst case is here - we see shadows to the far clipping plane of the camera.Code
voidcalculateMaxSplitDistances(){ float nearPlane = m_camera.getInternalCamera().GetNearPlane(); float farPlane = m_camera.getInternalCamera().GetFarPlane(); for (int i = 1; i < m_splitCount; i++) { float f = (float)i / (float)m_splitCount; float l = nearPlane * pow(farPlane / nearPlane, f); float u = nearPlane + (farPlane - nearPlane) * f; m_maxSplitDistances[i - 1] = l * m_splitLambda + u * (1.0f - m_splitLambda); } m_farPlane = farPlane + m_splitShift; } - We determine the distance between the camera and the farthest visible point of the object casting a shadow. It is important to note here that objects can cast and not cast shadows. For example, a flat-hilly landscape can be made not casting shadows, in this case, the lighting algorithm may be responsible for shading. Only objects casting shadows will be drawn into the shadow map.Code
floatcalculateFurthestPointInCamera(const matrix44& cameraView){ bbox3 scenebox; scenebox.begin_extend(); for (size_t i = 0; i < m_entitiesData.size(); i++) { if (m_entitiesData[i].isShadowCaster) { bbox3 b = m_entitiesData[i].geometry.lock()->getBoundingBox(); b.transform(m_entitiesData[i].model); scenebox.extend(b); } } scenebox.end_extend(); float maxZ = m_camera.getInternalCamera().GetNearPlane(); for (int i = 0; i < 8; i++) { vector3 corner = scenebox.corner_point(i); float z = -cameraView.transform_coord(corner).z; if (z > maxZ) maxZ = z; } returnstd::min(maxZ, m_farPlane); } - Based on the values obtained in steps 1 and 2, we determine the number of segments that we really need and the partition distances for them.Code
voidcalculateSplitDistances(){ // calculate how many shadow maps do we really need m_currentSplitCount = 1; if (!m_maxSplitDistances.empty()) { for (size_t i = 0; i < m_maxSplitDistances.size(); i++) { float d = m_maxSplitDistances[i] - m_splitShift; if (m_furthestPointInCamera >= d) m_currentSplitCount++; } } float nearPlane = m_camera.getInternalCamera().GetNearPlane(); for (int i = 0; i < m_currentSplitCount; i++) { float f = (float)i / (float)m_currentSplitCount; float l = nearPlane * pow(m_furthestPointInCamera / nearPlane, f); float u = nearPlane + (m_furthestPointInCamera - nearPlane) * f; m_splitDistances[i] = l * m_splitLambda + u * (1.0f - m_splitLambda); } m_splitDistances[0] = nearPlane; m_splitDistances[m_currentSplitCount] = m_furthestPointInCamera; } - For each segment (the boundaries of the segment are determined by the near and far distances), we calculate the bounding box.Code
bbox3 calculateFrustumBox(float nearPlane, float farPlane){ vector3 eye = m_camera.getPosition(); vector3 vZ = m_camera.getOrientation().z_direction(); vector3 vX = m_camera.getOrientation().x_direction(); vector3 vY = m_camera.getOrientation().y_direction(); float fov = n_deg2rad(m_camera.getInternalCamera().GetAngleOfView()); float aspect = m_camera.getInternalCamera().GetAspectRatio(); float nearPlaneHeight = n_tan(fov * 0.5f) * nearPlane; float nearPlaneWidth = nearPlaneHeight * aspect; float farPlaneHeight = n_tan(fov * 0.5f) * farPlane; float farPlaneWidth = farPlaneHeight * aspect; vector3 nearPlaneCenter = eye + vZ * nearPlane; vector3 farPlaneCenter = eye + vZ * farPlane; bbox3 box; box.begin_extend(); box.extend(vector3(nearPlaneCenter - vX * nearPlaneWidth - vY * nearPlaneHeight)); box.extend(vector3(nearPlaneCenter - vX * nearPlaneWidth + vY * nearPlaneHeight)); box.extend(vector3(nearPlaneCenter + vX * nearPlaneWidth + vY * nearPlaneHeight)); box.extend(vector3(nearPlaneCenter + vX * nearPlaneWidth - vY * nearPlaneHeight)); box.extend(vector3(farPlaneCenter - vX * farPlaneWidth - vY * farPlaneHeight)); box.extend(vector3(farPlaneCenter - vX * farPlaneWidth + vY * farPlaneHeight)); box.extend(vector3(farPlaneCenter + vX * farPlaneWidth + vY * farPlaneHeight)); box.extend(vector3(farPlaneCenter + vX * farPlaneWidth - vY * farPlaneHeight)); box.end_extend(); return box; } - We calculate the shadow matrix of the projection view for each segment.Code
matrix44 calculateShadowViewProjection(const bbox3& frustumBox){ constfloat LIGHT_SOURCE_HEIGHT = 500.0f; vector3 viewDir = m_camera.getOrientation().z_direction(); vector3 size = frustumBox.size(); vector3 center = frustumBox.center() - viewDir * m_splitShift; center.y = 0; auto lightSource = m_lightManager.getLightSource(0); vector3 lightDir = lightSource.orientation.z_direction(); matrix44 shadowView; shadowView.pos_component() = center - lightDir * LIGHT_SOURCE_HEIGHT; shadowView.lookatRh(shadowView.pos_component() + lightDir, lightSource.orientation.y_direction()); shadowView.invert_simple(); matrix44 shadowProj; float d = std::max(size.x, size.z); shadowProj.orthoRh(d, d, 0.1f, 2000.0f); return shadowView * shadowProj; }
We cut off objects using a simple test for the intersection of two bounding box (an object and a segment of the pyramid of visibility). There is one feature that is important to consider. We can not see the object, but see a shadow from it. It is easy to guess that with the approach described above we will cut off all objects that are not visible in the main camera, and there will be no shadows from them. To prevent this from happening, I used a fairly common technique - I pulled the bounding box of the object along the direction of light propagation, which gave a rough approximation of the area of space in which the shadow of the object is visible. As a result, an array of shadow map indices was created for each object into which this object should be drawn.
Code
voidupdateShadowVisibilityMask(const bbox3& frustumBox, conststd::shared_ptr<framework::Geometry3D>& entity, EntityData& entityData, int splitIndex){
bbox3 b = entity->getBoundingBox();
b.transform(entityData.model);
// shadow box computationauto lightSource = m_lightManager.getLightSource(0);
vector3 lightDir = lightSource.orientation.z_direction();
float shadowBoxL = fabs(lightDir.z) < 1e-5 ? 1000.0f : (b.size().y / -lightDir.z);
bbox3 shadowBox;
shadowBox.begin_extend();
for (int i = 0; i < 8; i++)
{
shadowBox.extend(b.corner_point(i));
shadowBox.extend(b.corner_point(i) + lightDir * shadowBoxL);
}
shadowBox.end_extend();
if (frustumBox.clipstatus(shadowBox) != bbox3::Outside)
{
int i = entityData.shadowInstancesCount;
entityData.shadowIndices[i] = splitIndex;
entityData.shadowInstancesCount++;
}
}
Now let's look at the rendering process and the specific parts for Direct3D 11 and OpenGL 4.3.
Direct3D 11 implementation
To implement the algorithm on Direct3D 11 we need:
- An array of textures for rendering shadow maps. To create this kind of object in the structure
D3D11_TEXTURE2D_DESCthere is a fieldArraySize. Thus, in C ++ code we will not have anything similar toID3D11Texture2D* array[N]. From the point of view of the Direct3D API, the texture array differs slightly from a single texture. An important feature when using such an array in a shader is that we can determine which texture in the array we will draw this or that object (semanticsSV_RenderTargetArrayIndexin HLSL). This is the main difference between this approach and MRT (multiple render targets), in which one object is drawn immediately into all the given textures. For objects that need to be drawn into several shadow cards at once, we will use hardware instancing, which allows us to clone objects at the GPU level. In this case, the object can be drawn into one texture in the array, and its clones into others. In shadow maps, we will only store the depth value, so we will use the texture formatDXGI_FORMAT_R32_FLOAT. - Special texture sampler. In the Direct3D API, you can set special parameters for sampling from the texture, which will allow you to compare the values in the texture with a given number. The result in this case will be 0 or 1, and the transition between these values can be smoothed out by a linear or anisotropic filter. To create a sampler in the structure,
D3D11_SAMPLER_DESCwe set the following parameters:samplerDesc.Filter = D3D11_FILTER_COMPARISON_MIN_MAG_LINEAR_MIP_POINT; samplerDesc.ComparisonFunc = D3D11_COMPARISON_LESS; samplerDesc.AddressU = D3D11_TEXTURE_ADDRESS_BORDER; samplerDesc.AddressV = D3D11_TEXTURE_ADDRESS_BORDER; samplerDesc.BorderColor[0] = 1.0f; samplerDesc.BorderColor[1] = 1.0f; samplerDesc.BorderColor[2] = 1.0f; samplerDesc.BorderColor[3] = 1.0f;
Thus, we will have bilinear filtering, comparison with the “less” function, and sampling from the texture by coordinates outside the range [0; 1] will return 1 (ie, no shadow).
We will render according to the following scheme:
- Clearing an array of shadow maps. Since the smallest distance between objects and the light source is stored in the shadow map, we will clear it with a value
FLT_MAX. - Render the scene into an array of shadow maps. To do this, we transfer to the shaders an array of shadow matrices of the projection view and an array of shadow map indices for each object. Objects that need to be drawn into several shadow maps are drawn with instantiation using the method
DrawIndexedInstanced. HLSL shaders for generating shadow maps are shown below.Vertex shader#include<common.h.hlsl>structVS_OUTPUT { float4 position : SV_POSITION; float depth : TEXCOORD0; uint instanceID : SV_InstanceID; }; VS_OUTPUT main(VS_INPUT input, unsignedint instanceID : SV_InstanceID){ VS_OUTPUT output; float4 pos = mul(float4(input.position, 1), model); output.position = mul(pos, shadowViewProjection[shadowIndices[instanceID]]); output.depth = output.position.z; output.instanceID = instanceID; return output; }Geometric shader#include<common.h.hlsl>structGS_INPUT { float4 position : SV_POSITION; float depth : TEXCOORD0; uint instanceID : SV_InstanceID; }; structGS_OUTPUT { float4 position : SV_POSITION; float depth : TEXCOORD0; uint index : SV_RenderTargetArrayIndex; }; [maxvertexcount(3)] voidmain(triangle GS_INPUT pnt[3], inout TriangleStream<GS_OUTPUT> triStream){ GS_OUTPUT p = (GS_OUTPUT)pnt[0]; p.index = shadowIndices[pnt[0].instanceID]; triStream.Append(p); p = (GS_OUTPUT)pnt[1]; p.index = shadowIndices[pnt[1].instanceID]; triStream.Append(p); p = (GS_OUTPUT)pnt[2]; p.index = shadowIndices[pnt[2].instanceID]; triStream.Append(p); triStream.RestartStrip(); }Pixel shaderstructPS_INPUT { float4 position : SV_POSITION; float depth : TEXCOORD0; uint index : SV_RenderTargetArrayIndex; }; floatmain(PS_INPUT input) : SV_TARGET { return input.depth; }
As a result, an array of shadow maps will look something like this.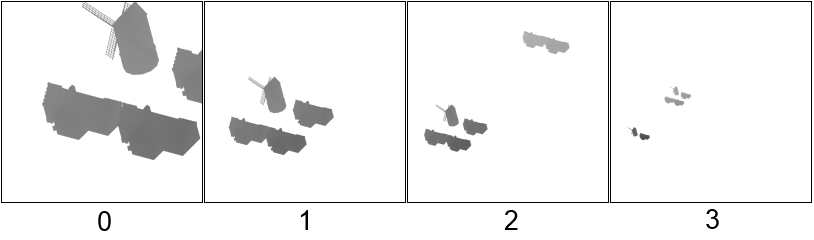
- Render the scene from the main camera. To make the shadow a little blurry, we use the Percentage Closer Filtering algorithm . When calculating the shadowing of the point, we will make samples from all shadow maps and mix the result. As a result, we get a float value, where 0.0 means a completely shaded point, and 1.0 means a completely unshaded point. The functions on HLSL for calculating shading are given below.
float3 getShadowCoords(int splitIndex, float3 worldPos){ float4 coords = mul(float4(worldPos, 1), shadowViewProjection[splitIndex]); coords.xy = (coords.xy / coords.ww) * float2(0.5, -0.5) + float2(0.5, 0.5); return coords.xyz; } floatsampleShadowMap(int index, float3 coords, float bias){ if (coords.x < 0 || coords.x > 1 || coords.y < 0 || coords.y > 1) return1.0f; float3 uv = float3(coords.xy, index); float receiver = coords.z; float sum = 0.0; constint FILTER_SIZE = 3; constfloat HALF_FILTER_SIZE = 0.5 * float(FILTER_SIZE); for (int i = 0; i < FILTER_SIZE; i++) { for (int j = 0; j < FILTER_SIZE; j++) { float3 offset = float3(shadowBlurStep * (float2(i, j) - HALF_FILTER_SIZE) / HALF_FILTER_SIZE, 0); sum += shadowMap.SampleCmpLevelZero(shadowMapSampler, uv + offset, receiver - bias); } } return sum / (FILTER_SIZE * FILTER_SIZE); } floatshadow(float3 worldPos){ float shadowValue = 0; [unroll(MAX_SPLITS)] for (int i = 0; i < splitsCount; i++) { float3 coords = getShadowCoords(i, worldPos); shadowValue += (1.0 - sampleShadowMap(i, coords, SHADOW_BIASES[i])); } return1.0 - saturate(shadowValue); }
Finally, it is necessary to take into account the fact that in addition to shadows, there is also shading from the lighting algorithm (I used the Blinn-Fong lighting model ). To prevent double shading, I added the following code to the pixel shader.float shadowValue = shadow(input.worldPos); shadowValue = lerp(1, shadowValue, ndol);
Here the advantage is given to the lighting model, i.e. where it is dark according to the Blinn-Fong model, the shadow will not be additionally applied. The solution does not claim to be ideal, but to some extent eliminates the problem.
As a result, we get the following picture.
OpenGL 4.3 implementation
To implement the algorithm on OpenGL 4.3, we need everything the same as for Direct3D 11, but there are subtleties. In OpenGL, we can make a selection combined with comparison only for textures containing a depth value (for example, in a format
GL_DEPTH_COMPONENT32F). Consequently, we will render only the depth buffer, and remove the color entry (more precisely, we will attach only an array of textures to the framebuffer to store the depth buffer). This, on the one hand, will save us a bit of video memory and facilitate the graphics pipeline, on the other hand, it will force us to work with normalized depth values. OpenGL's selection options can be mapped directly to a texture. They will be identical to those that were previously considered for Direct3D 11.
constfloat BORDER_COLOR[] = { 1.0f, 1.0f, 1.0f, 1.0f };
glBindTexture(m_shadowMap->getTargetType(), m_shadowMap->getDepthBuffer());
glTexParameteri(m_shadowMap->getTargetType(), GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);
glTexParameteri(m_shadowMap->getTargetType(), GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glTexParameteri(m_shadowMap->getTargetType(), GL_TEXTURE_COMPARE_MODE, GL_COMPARE_REF_TO_TEXTURE);
glTexParameteri(m_shadowMap->getTargetType(), GL_TEXTURE_COMPARE_FUNC, GL_LESS);
glTexParameteri(m_shadowMap->getTargetType(), GL_TEXTURE_WRAP_S, GL_CLAMP_TO_BORDER);
glTexParameteri(m_shadowMap->getTargetType(), GL_TEXTURE_WRAP_T, GL_CLAMP_TO_BORDER);
glTexParameterfv(m_shadowMap->getTargetType(), GL_TEXTURE_BORDER_COLOR, BORDER_COLOR);
glBindTexture(m_shadowMap->getTargetType(), 0);
An interesting process is the creation of an array of textures, which inside OpenGL is represented by a three-dimensional texture. They did not make a special function for its creation, and both are created using
glTexStorage3D. An analog SV_RenderTargetArrayIndexin GLSL is a built-in variable gl_Layer. The rendering scheme also remained the same:
- Clear the array of shadow cards. Since there is no color channel in the framebuffer, we will only clear the depth buffer. For a normalized depth buffer, the maximum value will be 1.0.
- Render shadow maps. Since only depth buffers are formed, we do not need a fragment shader.Vertex shader
#version 430 core const int MAX_SPLITS = 4; layout(location = 0) in vec3 position; layout(location = 1) in vec3 normal; layout(location = 2) in vec2 uv0; layout(location = 3) in vec3 tangent; layout(location = 4) in vec3 binormal; out VS_OUTPUT { float depth; flat int instanceID; } vsoutput; uniform mat4 modelMatrix; uniform mat4 shadowViewProjection[MAX_SPLITS]; uniform int shadowIndices[MAX_SPLITS]; void main() { vec4 wpos = modelMatrix * vec4(position, 1); vec4 pos = shadowViewProjection[shadowIndices[gl_InstanceID]] * vec4(wpos.xyz, 1); gl_Position = pos; vsoutput.depth = pos.z; vsoutput.instanceID = gl_InstanceID; }Geometric shader#version 430 coreconstint MAX_SPLITS = 4; layout(triangles) in; layout(triangle_strip, max_vertices = 3) out; in VS_OUTPUT { float depth; flat int instanceID; } gsinput[]; uniform int shadowIndices[MAX_SPLITS]; voidmain() { for (int i = 0; i < gl_in.length(); i++) { gl_Position = gl_in[i].gl_Position; gl_Layer = shadowIndices[gsinput[i].instanceID]; EmitVertex(); } EndPrimitive(); } - Render the scene from the main camera. When calculating the shading, the main thing is not to forget to translate the distance between the current point and the light source (
coords.zin the code) into the range [0; 1] .vec3 getShadowCoords(int splitIndex, vec3 worldPos) { vec4 coords = shadowViewProjection[splitIndex] * vec4(worldPos, 1); coords.xyz = (coords.xyz / coords.w) * vec3(0.5) + vec3(0.5); return coords.xyz; }
As a result, we get a picture slightly different from Direct3D 11 (for the sake of interest, I will show it from a different angle).
Problems
The shadow mapping algorithm and its modifications have many problems. Often the algorithm has to be carefully tuned for a specific game or even a specific scene. A list of the most common problems and solutions can be found here . When implementing PSSM, I came across the following:
- The disappearance of shadows from objects located behind the observer. We position shadow cards so that their coverage matches the pyramid of visibility from the main camera as much as possible. Accordingly, objects located behind the observer simply will not fall into them. I smoothed out this artifact by introducing a shift in the direction opposite to the vision vector in the algorithm for calculating shadow matrices of the projection view. Although this, of course, does not solve the problem in the case of long shadows at sunset or shadows from tall objects.
- Trimming shadows of objects. If the object is large enough, then it can partially be cut off when rendering the shadow map of the first segments. You can solve this by adjusting the position of the camera from which the shadow is rendered, and by shifting from the previous paragraph. With unsuccessful settings, you can see such an artifact.

- Erroneous self-shadowing. Probably the most famous graphic artifact arising from the use of shadow maps. This problem is quite successfully solved by introducing an error when comparing the value in the shadow map with the calculated value. In practice, I had to use individual error values for each shadow map. The figure below on the left shows an unfortunate choice of errors, on the right - a successful one.

- Unfortunately, eliminating false self-shadowing by introducing an error when comparing depths leads to another artifact called Peter Panning (you can roughly translate it into Russian as the “Peter Pan effect”). For those who do not remember the book, the shadow of Peter Pan lived his life and often ran away from the owner. It looks like this (the shadow on the corner of the house is slightly shifted).

This artifact is sometimes difficult to notice, especially on objects of complex shape, but it is almost always there.
Performance
Performance measurements were carried out on a computer with the following configuration: AMD Phenom II X4 970 3.79GHz, 16Gb RAM, AMD Radeon HD 7700 Series, running Windows 8.1.
Average frame time. Direct3D 11 / 1920x1080 / MSAA 8x / full screen / small scene (~ 12k polygons per frame, ~ 20 objects)
| Number of splits / Shadow map size (N x N pixels) | 1024 | 2048 | 4096 |
|---|---|---|---|
| 2 | 4.5546ms | 5.07555ms | 7.1661ms |
| 3 | 5.50837ms | 6.18023ms | 9.75103ms |
| four | 6.00958ms | 7.23269ms | 12.1952ms |
Average frame time. OpenGL 4.3 / 1920x1080 / MSAA 8x / full screen / small scene (~ 12k polygons per frame, ~ 20 objects)
| Number of splits / Shadow map size (N x N pixels) | 1024 | 2048 | 4096 |
|---|---|---|---|
| 2 | 3.2095ms | 4.05457ms | 6.06558ms |
| 3 | 3.9968ms | 4.87389ms | 8.65781ms |
| four | 4.68831ms | 5.93709ms | 10.4345ms |
Average frame time. 4 partitions / 1920x1080 / MSAA 8x / full screen / large scene (~ 1000k polygons per frame, ~ 1000 objects, ~ 500 object instances)
| API / Shadow Map Size (N x N pixels) | 1024 | 2048 | 4096 |
|---|---|---|---|
| Direct3D 11 | 29.2031ms | 33.3434ms | 40.5429ms |
| Opengl 4.3 | 21.0032ms | 26.4095ms | 41.8098ms |
The results showed that on large and small scenes, the implementation on OpenGL 4.3 works, in general, faster. With an increase in the load on the graphics pipeline (an increase in the number of objects and their instances, an increase in the size of shadow maps), the difference in the speed of work between implementations decreases. I associate the advantage of the OpenGL implementation with a different way of forming a shadow map than Direct3D 11 (we used only the depth buffer without writing to color). Nothing prevents us from doing the same on Direct3D 11, reconciled with the use of normalized depth values. However, this approach will work only until we want to store in the shadow map what additional data or a function of the depth value instead of the depth value. And some algorithm improvements (e.g. Variance Shadow Mapping) will turn out to be difficult for us to implement.
findings
The PSSM algorithm is one of the most successful ways to create shadows in large open spaces. It is based on a simple and understandable splitting principle, which can be easily scaled by increasing or decreasing the quality of shadows. This algorithm can be combined with other shadow mapping algorithms to obtain more beautiful soft shadows or physically more correct ones. At the same time, shadow mapping class algorithms often lead to the appearance of unpleasant graphic artifacts, which must be eliminated by fine-tuning the algorithm for a specific game.

