We increase the randomness of the fact that it is [probably] [almost] random

random numbers are tastier if they are slightly peppered.

We will combine theory with practice - we will show that it is possible to improve the entropy of random sequences, after which we will look at the source codes that do this.

I really wanted to write about the fact that high-quality, that is, highly entropic, random number generation is critically important in solving a huge number of problems, but this is probably superfluous. I hope everyone knows this very well.

In pursuit of qualitative random numbers, people invent very ingenious devices (see, for example, here and here). In principle, quite good sources of chance are built into the API of operating systems, but the matter is serious, and we are always a little bit worried about the worm of doubt: is the RNG good enough that I use, and is it not spoiled by third parties?

Little theory

To begin, let us show that with the right approach, the quality of the existing RNG cannot be degraded. The simplest correct approach is to overlay any other main sequence through the XOR operation. The main sequence may be, for example, a systemic RNG, which we already consider to be quite good, but there are still some doubts, and we have a desire to make sure. An additional sequence can be, for example, a pseudo-random number generator, the output of which looks good, but we know that its real entropy is very low. The resulting sequence will be the result of applying the XOR operation to the bits of the main and additional sequences. Significant nuance:main and additional sequences must be independent of each other. That is, their entropy must be taken from fundamentally different sources, the interdependence of which cannot be calculated.

Denote as x the next bit of the main sequence, and y - the corresponding bit of the additional sequence . Bit of the resulting sequence is denoted as r :
  r = x⊕y

The first attempt to prove. Let's try to go through the informational entropy x , y and r . The probability of zero x is denoted as p _x0 , and the probability of zero y as p_y0 . Informational entropies x and y are calculated by the Shannon formula:

  H_x= - (p_x0log₂p_x0+ (1 − p_x0) log₂(1 − p_x0))
  H_y= - (p_y0log₂p_y0+ ( 1 − p_y0) log₂(1 − p_y0)) A

zero in the resulting sequence appears when the input has two zeros or two ones. The probability of zero r:

  p_r0= p_x0p_y0+ (1 − p _x0 ) (1 − p _y0 )
  H _r = - (p _r0 log ₂ p _r0 + (1 − p _r0 ) log ₂ (1 − p _r0 ))

In order to prove the non-deterioration of the main sequence, prove that
Hr - Hx ≥ 0 for any values of p _x0 and p _y0 . Analytically, I failed to prove this, but the visualized calculation shows that the increase in entropy forms a smooth surface, which is not going anywhere to go to minus:

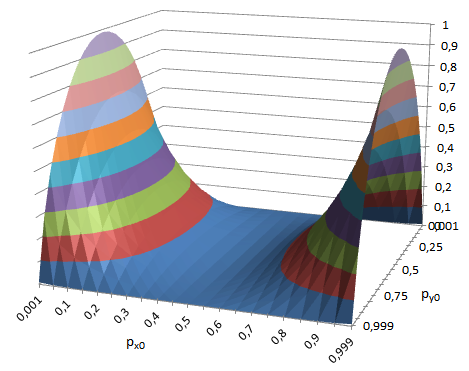
For example, if we add a strongly skewed additional with p _y0 = 0.1 to the skewed main signal c p _x0 = 0.3 (entropy 0.881) , we get the result p _r0 = 0.66 with entropy 0.925. So, entropy cannot be spoiled, but this is not yet accurate. Therefore, we need a second attempt. However, through entropy, it is also possible to carry out the proof. Scheme (all steps are quite simple, you can do it yourself):

We prove that the entropy has a maximum at the point p ₀ = 1/2.
We prove that for any p _x0 and p _{y0, the} value of p _r0 cannot be further from 1/2 than p _x0 .

The second attempt to prove. Through the ability to guess. Suppose an attacker has a priori some information about the main and additional sequences. The possession of information is expressed in the ability with some probability to guess in advance the values of x , y and, as a result, r . The probabilities of guessing x and y are denoted respectively by g _x and g _y (from the word guess). The bit of the resulting sequence is guessed either when both values are correctly guessed or when both are wrong, therefore the probability of guessing is:
g _r = g _x g_y + (1 − g _x ) (1 − g _y ) = 2 g _x g _y - g _x - g _y + 1

When we have a perfect guess, we have g = 1. If we don’t know anything, g is ... no, not zero, but 1/2. It is this probability of guessing is obtained if we make a decision by tossing a coin. A very interesting case is when g <1/2. On the one hand, such a diviner somewhere inside itself has data about the predictable value, but for some reason it inverts its output, and thus it becomes worse than a coin.. Please remember the phrase “worse than a coin,” it will be useful to us below. From the point of view of the mathematical theory of communication (and, as a result, the quantitative information theory we are used to), this situation is absurd, since it will no longer be information theory, but disinformation theory, but in life we have this situation more often than we would like .

Consider the limiting cases:

g _x = 1 , that is, the sequence x is completely predictable:
g_r = g_x g_y + (1 − g_x ) (1 − g_y ) = 1 g_y + (1 - 1) (1 − g_y ) = g_y
That is, the probability of guessing the result is equal to the probability of guessing the additional sequence.
g _y = 1 : Same as above. The probability of guessing the result is equal to the probability of guessing the main sequence.
g _x = 1/2 , that is, the sequence x is completely unpredictable:
g_r = 2 g_x g_y - g_x - g_y + 1 = 2/2 g_y - 1/2 - g_y +1 = g_y - g_y + 1/2 = 1/2
That is, the addition of any additional sequence does not impair the overall unpredictability of the main one.
g _y = 1/2 : Same as above. Adding a completely unpredictable extra sequence makes the result completely unpredictable.

In order to prove that adding an additional sequence to the main one will not help the attacker, we need to find out under what conditions g _r can be greater than g _x , that is,

  2 g _x g _y - g _x - g _y + 1> g _x

Transfer g _x from the right to the left, and g _y and 1 to the right:

  2 g _x g _y - g _x - g _x > g _y - 1
  2 g _x g _y - 2 g _x > g_y - 1
On the left side we put 2g _x for the brackets:
  2 g _x (g _y - 1)> g _y - 1
Since we have g _y less than one (the limiting case, when g _y = 1, we have already considered), we will turn g _y −1 to 1 − g _y , not forgetting to change “more” to “less”:
  2 g _x (1 - g _y ) <1 - g _{y We}

shorten “1 − g _y ” and get the condition under which adding an additional sequences will improve the attacker's guessing situation:

  2 g _x <1
  g _x<1/2

That is, g _r can be greater than g _x only when the guessing of the main sequence is worse than a coin . Then, when our predictor is busy conscious sabotage.

Some additional considerations about entropy.

Entropy is an extremely mythologized concept. Informational - including. It really hinders. Often, informational entropy is represented as a kind of subtle matter that is either objectively present in the data or not. In fact, informational entropy is not something that is present in the signal itself, but a quantitative assessment of the a priori awareness of the recipient of the message about the message itself. That is, it is not only about the signal, but also about the recipient. If the recipient knows nothing about the signal at all, the information entropy of the transmitted binary unit is exactly 1 bit regardless of how the signal was received and what it is.
We have an entropy addition theorem, according to which the total entropy of independent sources is equal to the sum of the entropies of these sources. If we connected the main sequence with the additional through the concatenation, we would save the entropies of the sources, but we would get a bad result, because in our problem we need to estimate not the total entropy, but the specific entropy, in terms of a separate bit. The concatenation of sources gives us the specific entropy of the result, equal to the arithmetic mean of the sources, and the entropy weak additional sequence naturally worsens the result. The use of XOR operation leads to the fact that we lose some of the entropy, but we are guaranteed to have a resultant entropy no worse than the maximum entropy of the terms.
Cryptographers have a dogma: the use of pseudo-random number generators is an unforgivable arrogance. Because these generators have a small specific entropy. But we just found out that if you do everything right, entropy becomes a barrel of honey, which cannot be spoiled by any amount of tar.
If we have only 10 bytes of real entropy, spread over a kilobyte of data, from a formal point of view, we have only 1% of specific entropy, which is very bad. But if these 10 bytes are spread out qualitatively, and apart from brute force there is no way to calculate these 10 bytes, everything does not look so bad. 10 bytes is 2 ⁸⁰ , and if our brute force per second goes through a trillion variants, we will need an average of 19 thousand years to learn how to guess the next character.

As mentioned above, informational entropy is a relative value. Where for one subject the specific entropy is 1, for another it may well be 0. Moreover, the one from whom 1 may have no way of knowing the true state of affairs. Systemic RNG gives a stream that is indistinguishable for us from a truly random one, but we can only hope that it is really random for everyone . And believe. If paranoia suggests that the quality of the main RNG may suddenly turn out to be unsatisfactory, it makes sense to err with an extra.

Implementation of the summing RNG on Python

from random import Random, SystemRandom
from random import BPF as _BPF, RECIP_BPF as _RECIP_BPF
from functools import reduce as _reduce
from operator import xor as _xor
classCompoundRandom(SystemRandom):def__new__(cls, *sources):"""Positional arguments must be descendants of Random"""ifnot all(isinstance(src, Random) for src in sources):
            raise TypeError("all the sources must be descendants of Random")
        return super().__new__(cls)
    def__init__(self, *sources):"""Positional arguments must be descendants of Random"""
        self.sources = sources
        super().__init__()
    defgetrandbits(self, k):"""getrandbits(k) -> x.  Generates an int with k random bits."""######## На самом деле всё это ради вот этой строчки:return _reduce(_xor, (src.getrandbits(k) for src in self.sources), 0)
    defrandom(self):"""Get the next random number in the range [0.0, 1.0)."""######## Не понятно, почему в SystemRandom так не сделано. Ну ладно...return self.getrandbits(_BPF) * _RECIP_BPF

Example of use:

>>> import random_xe # <<< Так оно называется>>> from random import Random, SystemRandom
>>> # Создаём объект:>>> myrandom1 = random_xe.CompoundRandom(SystemRandom(), Random())
>>> # Используем как обычный Random:>>> myrandom1.random()
0.4092251189581082>>> myrandom1.randint(100, 200)
186>>> myrandom1.gauss(20, 10)
19.106991205743107

The main stream is taken to be considered the correct SystemRandom, and as an additional - standard PRNG Random. The meaning of this, of course, is not very much. A standard PRNG is definitely not the supplement for which all this was worth starting up. You can instead marry two system RNGs together:

>>> myrandom2 = random_xe.CompoundRandom(SystemRandom(), SystemRandom())

It makes sense, though this is even less (although it is such a technique that Bruce Schneier recommends in Applied Cryptography for some reason), because the above calculations are valid only for independent sources. If the system’s RNG is compromised, the result will also be compromised. In principle, the flight of fantasy in the search for a source of additional entropy is not limited by anything (in our world, confusion is much more common than order), but as a simple solution I will offer the PRNG HashRandom, also implemented in the random_xe library.

PRNG based streaming cyclic hashing

In the simplest case, you can take a relatively small amount of initial data (for example, ask the user to drum on the keyboard), calculate their hash, and then cyclically add a hash to the input of the hashing algorithm and take the following hashes. Schematically, this can be represented as:

The cryptoresistance of this process is based on two assumptions:

The task of restoring the original data to the hash value is unbearably difficult.
According to the hash value, it is impossible to restore the internal state of the hashing algorithm.

After consulting with the internal paranoid, he recognized the second assumption as superfluous, and therefore the scheme is a bit complicated in the final implementation of the PRNG:

Now, if an attacker managed to get the value “Hash 1r”, he will not be able to calculate the next value “Hash 2r”, since he does not have the value “Hash 2h”, which he cannot find out without calculating the counter-hashing function. Thus, the cryptographic stability of this scheme corresponds to the cryptographic stability of the hashing algorithm used.

Example of use:

>>> # Создаём объект, проинициализировав HashRandom лучшим в мире паролем '123':>>> myrandom3 = random_xe.CompoundRandom(SystemRandom(), random_xe.HashRandom('123'))
>>> # Используем как обычный Random:>>> myrandom3.random()
0.8257149881148604

The default algorithm is SHA-256. If you want something else, you can transfer the desired type of hashing algorithm to the constructor using the second parameter. For example, let's make a composite RNG, summing up the following:

1. Systemic RNG (this is sacred).
2. User input processed by the SHA3-512 algorithm.
3. The time spent on this input processed by SHA-256.

>>> from getpass import getpass
>>> from time import perf_counter
>>> from hashlib import sha3_512
# Оформим в виде функции:>>> defsuper_myrandom():
    t_start = perf_counter()
    return random_xe.CompoundRandom(SystemRandom(),
        random_xe.HashRandom(
            getpass('Побарабаньте по клавиатуре:'), sha3_512),
        random_xe.HashRandom(perf_counter() - t_start))
>>> myrandom4 = super_myrandom()
Побарабаньте по клавиатуре:
>>> myrandom4.random()
0.35381173716740766

Findings:

If we are not sure of our random number generator, we can easily and incredibly cheaply solve this problem.
Solving this problem, we will not be able to make it worse. Only better. And it is mathematically proven.
One should not forget to try to make the used sources of entropy independent.

The sources of the library are on GitHub .

Tags:

We increase the randomness of the fact that it is [probably] [almost] random

Little theory

Implementation of the summing RNG on Python

PRNG based streaming cyclic hashing

Also popular now: