How and why we wrote a highly loaded scalable service for 1C: Enterprises: Java, PostgreSQL, Hazelcast
In this article, we will talk about how and why we developed the Interaction System - a mechanism that transfers information between client applications and 1C: Enterprise servers - from setting a task to thinking through the architecture and implementation details.
The Interaction System (hereinafter - CB) is a distributed fault-tolerant messaging system with guaranteed delivery. SV is designed as a highly loaded service with high scalability, and is available as an online service (provided by 1C), and as a lottery product that can be deployed on its server capacities.
CB uses Hazelcast distributed storage and search engine Elasticsearch. We will also discuss Java and how we horizontally scale PostgreSQL.

To make it clear why we did the Interaction System, I’ll tell you a little about how the development of business applications in 1C is arranged.
For a start - a little about us for those who still do not know what we are doing :) We are making the 1C: Enterprise technology platform. The platform includes a business application development tool, as well as a runtime that allows business applications to work in a cross-platform environment.
Business applications created on 1C: Enterprise operate in a three-tier client / server architecture “DBMS - Application Server - Client”. The application code written in the embedded language 1C can be executed on the application server or on the client. All work with application objects (directories, documents, etc.), as well as reading and writing the database is performed only on the server. The functionality of the forms and the command interface is also implemented on the server. The client receives, opens and displays forms, “communicates” with the user (warnings, questions ...), makes small calculations in forms that require quick reaction (for example, multiplying prices by quantity), working with local files, working with equipment.
In the application code, the headers of the procedures and functions must explicitly indicate where the code will be executed - using the & OnClient / & OnServer directives (& AtClient / & AtServer in the English language version). The 1C developers will now correct me, saying that there are actually more directives , but for us this is not essential now.
You can call the server code from the client code, but you cannot call the client code from the server code. This is a fundamental limitation made by us for a number of reasons. In particular, because the server code must be written in such a way that it will be executed equally from wherever it is called - from the client or from the server. And in the case of calling the server code from another server code, the client is missing as such. And because during the execution of the server code, the client that called it could close, exit the application, and the server will have no one to call.
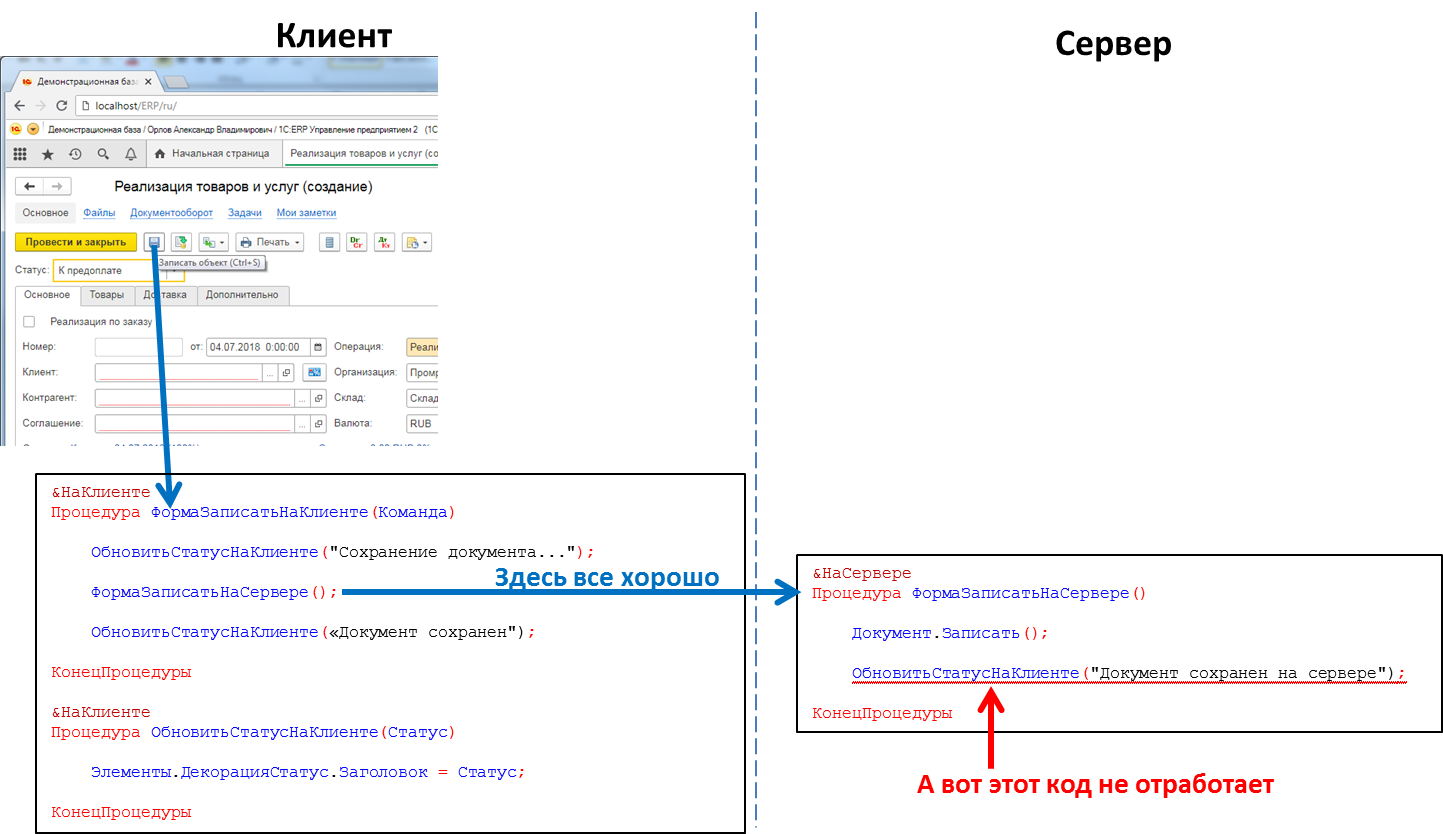
The code that handles button presses: a call to the server procedure from the client will work, a call to the client procedure from the server - no
This means that if we want to send some message from the server to the client application, for example, that the formation of a “long-playing” report has finished and the report can be viewed - we have no such method. We have to go for tricks, for example, periodically polling the server from client code. But this approach loads the system with unnecessary calls, and in general does not look very elegant.
And there is also a need, for example, when a received SIP telephone call arrives, to notify the client application about it, so that it will find the caller's number in the counterparty database and show the user information about the calling counterparty. Or, for example, when arriving at the warehouse of the order to notify the client application of the customer. In general, there are a lot of cases where such a mechanism would be useful.
Create a messaging mechanism. Fast, reliable, with guaranteed delivery, with the possibility of flexible message retrieval. On the basis of the mechanism to implement an instant messenger (messages, video calls) that runs inside 1C applications.
Design the system horizontally scalable. Increasing load must be closed by increasing the number of nodes.
We decided not to build the server part of SV into the 1C: Enterprise platform, but to implement it as a separate product, whose API can be called from the 1C application solution code. This was done for a number of reasons, the main of which was to make it possible to exchange messages between different 1C applications (for example, between the Office of Trade and Accounting). Different 1C applications can work on different versions of the 1C: Enterprise platform, reside on different servers, etc. In such conditions, the implementation of the SV as a separate product located “on the side” of 1C installations is the optimal solution.
So, we decided to do SV as a separate product. We recommend that small companies use the CB server that we installed in our cloud (wss: //1cdialog.com) to avoid the overhead associated with installing and configuring the server locally. Large clients may consider it expedient to install their own CB server at their facilities. We used a similar approach in our cloud SaaS product 1cFresh - it is released as a lottery product for installation with customers, and also deployed in our cloud https://1cfresh.com/ .
For load balancing and fault tolerance, we will deploy not one Java application, but several; we will put a load balancer in front of them. If you need to send a message from node to node, use publish / subscribe in Hazelcast.
Client communication with the server - by websocket. It is well suited for real-time systems.
Choose between Redis, Hazelcast and Ehcache. In the yard in 2015. Redis just released a new cluster (too new, scary), there is a Sentinel with a bunch of restrictions. Ehcache does not know how to assemble into a cluster (this functionality appeared later). We decided to try with Hazelcast 3.4.
Hazelcast is going to cluster out of the box. In the single node mode, it is not very useful and can only fit as a cache - it does not know how to dump data to disk, if it lost a single node - it lost data. We deploy several Hazelcasts, between which we back up critical data. Cache is not backed up - it is not a pity.
For us, Hazelcast is:
Checked that there is no channel. They took the lock, again checked, created. If you do not check after taking the lock, then there is a chance that another thread at this moment also checked and will now try to create the same discussion - and it already exists. You cannot block using synchronized or regular java Lock. Through the base - slowly, and the base is pitiful, through the Hazelcast - what we need.
We have a large and successful experience with PostgreSQL and cooperation with the developers of this DBMS.
With a cluster, PostgreSQL is not easy - there are XL , XC , Citus , but, in general, this is not noSQL, which scale out of the box. NoSQL as the main repository was not considered, it was enough that we take Hazelcast, with which we have not worked before.
If you need to scale the relational database, it means sharding . As you know, with sharding, we divide the database into separate parts so that each of them can be transferred to a separate server.
The first version of our sharding suggested the possibility of spreading each of the tables of our application across different servers in different proportions. There are a lot of messages on server A — please, let's transfer part of this table to server B. Such a solution just screamed about premature optimization, so we decided to limit ourselves to a multi-tenant approach.
You can read about multi-tenant, for example, on the Citus Data website .
In NE there are concepts of the application and subscriber. An application is a specific installation of a business application, such as ERP or Accounting, with its users and business data. A subscriber is an organization or an individual on whose behalf the application is registered in the CB server. A subscriber can have several applications registered, and these applications can exchange messages with each other. The subscriber and became a tenant in our system. Messages of several subscribers can be in the same physical database; if we see that a subscriber began to generate a lot of traffic, we bring it to a separate physical database (or even a separate database server).
We have the main database where the routing table is stored with information about the location of all subscriber databases.

So that the main database is not a bottleneck, we keep the routing table (and other frequently requested data) in the cache.
If the subscriber’s database starts to slow down, we’ll cut the partitions inside. On other projects for the partitioning of large tables using pg_pathman .
Since losing users' messages is bad, we support our databases with replicas. The combination of synchronous and asynchronous replicas allows you to hedge against the loss of the main database. The message will be lost only in case of simultaneous failure of the main database and its synchronous replica.
If a synchronous replica is lost, the asynchronous replica becomes synchronous.
If the primary database is lost, the synchronous replica becomes the primary database, the asynchronous replica becomes the synchronous replica.
Since, among other things, CB is also an instant messenger, we need a quick, convenient and flexible search, taking into account the morphology, by inaccurate correspondences. We decided not to reinvent the wheel and use the free search engine Elasticsearch, based on the Lucene library . We also expand Elasticsearch in a cluster (master - data - data) to eliminate problems in case of failure of application nodes.
On github, we found a Russian morphology plugin for Elasticsearch and use it. In the Elasticsearch index, we store the roots of the words (which the plugin defines) and the N-grams. As the user enters the text for the search, we are looking for typed text among N-grams. When you save to the index, the word "texts" is divided into the following N-grams:
[those, tech, tex, text, texts, ek, ex, exts, exts, ks, ksts, cpsy, art, shty, you],
And also the root of the word "text" will be saved. This approach allows you to search and at the beginning, and in the middle, and at the end of the word.
Repeat pictures from the beginning of the article, but with explanations:
During the development and testing of CB, we encountered a number of interesting features of the products used by us.
The release of each CB release is load testing. It was successful when:
We fill the test database with data - to do this, we receive information from the production server about the most active subscriber, multiply its numbers by 5 (the number of messages, discussions, users) and so we test.
We carry out load testing of the interaction system in three configurations:
In the stress test, we run several hundred threads, and those without stopping load the system: write messages, create discussions, get a list of messages. We simulate the actions of ordinary users (get a list of my unread messages, write to someone) and software solutions (send a package of another configuration, handle the alert).
For example, this is how a part of the stress test looks like:
The “Only Connections” scenario did not appear for nothing. There is a situation: users have connected the system, but have not yet been involved. Each user at 09:00 in the morning turns on the computer, establishes a connection with the server and is silent. These guys are dangerous, there are many of them - from the packages they have only PING / PONG, but they keep the connection to the server (they can't keep it - and what if a new message). The test reproduces the situation when in half an hour a large number of such users try to log in to the system. It looks like a stress test, but the focus is on this first entry - so that there are no failures (the person does not use the system, and it already falls off - it’s hard to think of something worse).
The subscriber registration script originates from the first launch. We conducted a stress test and were confident that the system does not slow down in correspondence. But users went and started to fall off registration by timeout. During registration, we used / dev / random , which is tied to the entropy of the system. The server did not have time to save enough entropy, and when it requested a new SecureRandom it would freeze for tens of seconds. There are many ways out of this situation, for example: switch to a less secure / dev / urandom, put a special fee that forms entropy, generate random numbers in advance and store in a pool. We have temporarily closed the problem with a pool, but since then we have run a separate test for registering new subscribers.
We use JMeter as a load generator.. He doesn’t know how to work with a web-application; we need a plugin. The first in search results for the query “jmeter websocket” are articles from BlazeMeter , which recommend a plugin from Maciej Zaleski .
We decided to start with it.
Almost immediately after the start of serious testing, we discovered that memory leaks started in JMeter.
The plugin is a separate big story, with 176 stars it has 132 forks on github. The author himself does not commit it since 2015 (we took it in 2015, then it did not arouse suspicion), several github issues about memory leaks, 7 unclosed pull request-s.
If you decide to do load testing with this plugin, pay attention to the following discussions:
This is one of those on github. What we did:
And yet it flows!
Memory began to end not in a day, but in two. There was no time left, we decided to run fewer threads, but on four agents. This should have been enough for at least a week.
Two days passed ...
Now the memory began to end with Hazelcast. In the logs, it was clear that after a couple of days of testing, Hazelcast begins to complain about the lack of memory, and after some time the cluster falls apart, and the nodes continue to die one by one. We connected JVisualVM to the hazelcast and saw the “ascending saw” - he regularly called the GC, but could not clear the memory.
It turned out that in hazelcast 3.4 when deleting map / multiMap (map.destroy ()) the memory is not completely freed:
github.com/hazelcast/hazelcast/issues/6317
github.com/hazelcast/hazelcast/issues/4888
Now the bug is fixed in 3.5, but then it was a problem. We created new multiMap with dynamic names and deleted it according to our logic. The code looked like this:
Call:
MultiMap was created for each subscription and was deleted when it was not needed. We decided that we will start Map <String, Set>, the key will be the name of the subscription, and the identifiers of the sessions as values (which can then be used to get user IDs, if necessary).
The charts straightened.
Hazelcast for us was a new product, we started working with it from version 3.4.1, now version 3.9.2 is on our production server (at the time of this writing, the latest version of Hazelcast is 3.10).
We started with integer ids. Let's imagine that we need another Long for a new entity. Sequence in DB is not suitable, tables participate in sharding - it turns out that there is a message ID = 1 in DB1 and a message ID = 1 in DB2, in Elasticsearch you can’t put it on this ID, in Hazelcast too, but the worst thing is if you want to reduce the data from two databases to one (for example, deciding that one base is enough for these subscribers). You can start several AtomicLongs in Hazelcast and keep the counter there, then the performance of getting a new ID is incrementAndGet plus the time for a query in Hazelcast. But in Hazelcast there is something more optimal - FlakeIdGenerator. Each client is issued with a range of IDs, for example, the first is from 1 to 10,000, the second is from 10,001 to 20,000, and so on. Now the client can issue new identifiers independently, until the range given to him ends. It works quickly, but when the application is restarted (and the Hazelcast client), a new sequence begins - hence omissions, etc. In addition, developers are not very clear why the ID is an integer, but they are so much at odds. We all weighed and switched to UUIDs.
By the way, for those who want to be like Twitter, there is such a Snowcast library - this is the implementation of Snowflake on top of Hazelcast. You can see it here:
github.com/noctarius/snowcast
github.com/twitter/snowflake
But we have not reached our hands.
Another surprise: TransactionalMap.replace is not working. Here is a test:
I had to write my replace using getForUpdate:
Test not only regular data structures, but also their transactional versions. It happens that IMap works, and TransactionalMap is no longer there.
At first we decided to record objects of our classes in Hazelcast. For example, we have an Application class, we want to save and read it. Save:
We read:
Everything is working. Then we decided to build an index in Hazelcast, to look for it:
And when writing a new entity, we started getting ClassNotFoundException. Hazelcast tried to supplement the index, but knew nothing about our class and wanted to have a JAR planted with this class. We did it, it all worked, but a new problem appeared: how to update the JAR without completely stopping the cluster? Hazelcast does not pick up a new JAR with a new update. At this point, we decided that we could live without index search. After all, if you use Hazelcast as a key-value type storage, then everything will work? Not really. Here again the different behavior of IMap and TransactionalMap. Where IMap doesn't care, TransactionalMap throws an error.
IMap. We write down 5000 objects, we read. Everything is expected.
And in the transaction does not work, we get a ClassNotFoundException:
In 3.8, the User Class Deployment mechanism appeared. You can assign one master node and update the JAR file on it.
Now we have completely changed the approach: we serialize ourselves into JSON and save to Hazelcast. Hazelcast does not need to know the structure of our classes, and we can be updated without downtime. Versioning of domain objects is controlled by the application. At the same time, different versions of the application can be launched, and it is possible that a new application writes objects with new fields, but the old one does not know about these fields. And at the same time, the new application reads objects written by the old application, in which there are no new fields. We handle such situations inside the application, but for simplicity we do not change or delete fields, we only expand classes by adding new fields.
Going for data in the cache is always better than in the database, but you do not want to store unclaimed records either. The decision that to cache, we postpone for the last stage of development. When the new functionality is encoded, we enable logging of all requests (log_min_duration_statement to 0) in PostgreSQL and run load testing for 20 minutes. Using the collected logs, utilities like pgFouine and pgBadger can build analytical reports. In the reports we are primarily looking for slow and frequent requests. For slow queries, we build an execution plan (EXPLAIN) and evaluate whether such a query can be accelerated. Frequent requests for the same input data fit well into the cache. We try to keep the requests “flat”, one table in the request.
SV as an online service was launched in the spring of 2017, as a separate SV product was released in November 2017 (at that time in beta status).
For more than a year of operation, there were no serious problems with the operation of the SV online service. Online service is monitored via Zabbix , assembled and deployed from Bamboo .
The CB distribution package is delivered in the form of native packages: RPM, DEB, MSI. Plus for Windows, we provide a single installer in the form of a single EXE, which installs the server, Hazelcast and Elasticsearch on one machine. At first we called this version of the installation “demo”, but now it has become clear that this is the most popular deployment option.
The Interaction System (hereinafter - CB) is a distributed fault-tolerant messaging system with guaranteed delivery. SV is designed as a highly loaded service with high scalability, and is available as an online service (provided by 1C), and as a lottery product that can be deployed on its server capacities.
CB uses Hazelcast distributed storage and search engine Elasticsearch. We will also discuss Java and how we horizontally scale PostgreSQL.

Formulation of the problem
To make it clear why we did the Interaction System, I’ll tell you a little about how the development of business applications in 1C is arranged.
For a start - a little about us for those who still do not know what we are doing :) We are making the 1C: Enterprise technology platform. The platform includes a business application development tool, as well as a runtime that allows business applications to work in a cross-platform environment.
Client-server development paradigm
Business applications created on 1C: Enterprise operate in a three-tier client / server architecture “DBMS - Application Server - Client”. The application code written in the embedded language 1C can be executed on the application server or on the client. All work with application objects (directories, documents, etc.), as well as reading and writing the database is performed only on the server. The functionality of the forms and the command interface is also implemented on the server. The client receives, opens and displays forms, “communicates” with the user (warnings, questions ...), makes small calculations in forms that require quick reaction (for example, multiplying prices by quantity), working with local files, working with equipment.
In the application code, the headers of the procedures and functions must explicitly indicate where the code will be executed - using the & OnClient / & OnServer directives (& AtClient / & AtServer in the English language version). The 1C developers will now correct me, saying that there are actually more directives , but for us this is not essential now.
You can call the server code from the client code, but you cannot call the client code from the server code. This is a fundamental limitation made by us for a number of reasons. In particular, because the server code must be written in such a way that it will be executed equally from wherever it is called - from the client or from the server. And in the case of calling the server code from another server code, the client is missing as such. And because during the execution of the server code, the client that called it could close, exit the application, and the server will have no one to call.

The code that handles button presses: a call to the server procedure from the client will work, a call to the client procedure from the server - no
This means that if we want to send some message from the server to the client application, for example, that the formation of a “long-playing” report has finished and the report can be viewed - we have no such method. We have to go for tricks, for example, periodically polling the server from client code. But this approach loads the system with unnecessary calls, and in general does not look very elegant.
And there is also a need, for example, when a received SIP telephone call arrives, to notify the client application about it, so that it will find the caller's number in the counterparty database and show the user information about the calling counterparty. Or, for example, when arriving at the warehouse of the order to notify the client application of the customer. In general, there are a lot of cases where such a mechanism would be useful.
Actually staging
Create a messaging mechanism. Fast, reliable, with guaranteed delivery, with the possibility of flexible message retrieval. On the basis of the mechanism to implement an instant messenger (messages, video calls) that runs inside 1C applications.
Design the system horizontally scalable. Increasing load must be closed by increasing the number of nodes.
Implementation
We decided not to build the server part of SV into the 1C: Enterprise platform, but to implement it as a separate product, whose API can be called from the 1C application solution code. This was done for a number of reasons, the main of which was to make it possible to exchange messages between different 1C applications (for example, between the Office of Trade and Accounting). Different 1C applications can work on different versions of the 1C: Enterprise platform, reside on different servers, etc. In such conditions, the implementation of the SV as a separate product located “on the side” of 1C installations is the optimal solution.
So, we decided to do SV as a separate product. We recommend that small companies use the CB server that we installed in our cloud (wss: //1cdialog.com) to avoid the overhead associated with installing and configuring the server locally. Large clients may consider it expedient to install their own CB server at their facilities. We used a similar approach in our cloud SaaS product 1cFresh - it is released as a lottery product for installation with customers, and also deployed in our cloud https://1cfresh.com/ .
application
For load balancing and fault tolerance, we will deploy not one Java application, but several; we will put a load balancer in front of them. If you need to send a message from node to node, use publish / subscribe in Hazelcast.
Client communication with the server - by websocket. It is well suited for real-time systems.
Distributed cache
Choose between Redis, Hazelcast and Ehcache. In the yard in 2015. Redis just released a new cluster (too new, scary), there is a Sentinel with a bunch of restrictions. Ehcache does not know how to assemble into a cluster (this functionality appeared later). We decided to try with Hazelcast 3.4.
Hazelcast is going to cluster out of the box. In the single node mode, it is not very useful and can only fit as a cache - it does not know how to dump data to disk, if it lost a single node - it lost data. We deploy several Hazelcasts, between which we back up critical data. Cache is not backed up - it is not a pity.
For us, Hazelcast is:
- User session repository. Each time, going after the session to the base is a long time, so we put all the sessions in the Hazelcast.
- Cache. Looking for a user profile - check in the cache. Wrote a new message - put in the cache.
- Topics for communication instances of the application. The node generates an event and puts it in the Hazelcast topic. Other application nodes subscribed to this topic receive and process the event.
- Cluster lock. For example, we create a discussion using a unique key (a singleton discussion within the 1C database):
conversationKeyChecker.check("БЕНЗОКОЛОНКА");
doInClusterLock("БЕНЗОКОЛОНКА", () -> {
conversationKeyChecker.check("БЕНЗОКОЛОНКА");
createChannel("БЕНЗОКОЛОНКА");
});Checked that there is no channel. They took the lock, again checked, created. If you do not check after taking the lock, then there is a chance that another thread at this moment also checked and will now try to create the same discussion - and it already exists. You cannot block using synchronized or regular java Lock. Through the base - slowly, and the base is pitiful, through the Hazelcast - what we need.
Choosing a DBMS
We have a large and successful experience with PostgreSQL and cooperation with the developers of this DBMS.
With a cluster, PostgreSQL is not easy - there are XL , XC , Citus , but, in general, this is not noSQL, which scale out of the box. NoSQL as the main repository was not considered, it was enough that we take Hazelcast, with which we have not worked before.
If you need to scale the relational database, it means sharding . As you know, with sharding, we divide the database into separate parts so that each of them can be transferred to a separate server.
The first version of our sharding suggested the possibility of spreading each of the tables of our application across different servers in different proportions. There are a lot of messages on server A — please, let's transfer part of this table to server B. Such a solution just screamed about premature optimization, so we decided to limit ourselves to a multi-tenant approach.
You can read about multi-tenant, for example, on the Citus Data website .
In NE there are concepts of the application and subscriber. An application is a specific installation of a business application, such as ERP or Accounting, with its users and business data. A subscriber is an organization or an individual on whose behalf the application is registered in the CB server. A subscriber can have several applications registered, and these applications can exchange messages with each other. The subscriber and became a tenant in our system. Messages of several subscribers can be in the same physical database; if we see that a subscriber began to generate a lot of traffic, we bring it to a separate physical database (or even a separate database server).
We have the main database where the routing table is stored with information about the location of all subscriber databases.

So that the main database is not a bottleneck, we keep the routing table (and other frequently requested data) in the cache.
If the subscriber’s database starts to slow down, we’ll cut the partitions inside. On other projects for the partitioning of large tables using pg_pathman .
Since losing users' messages is bad, we support our databases with replicas. The combination of synchronous and asynchronous replicas allows you to hedge against the loss of the main database. The message will be lost only in case of simultaneous failure of the main database and its synchronous replica.
If a synchronous replica is lost, the asynchronous replica becomes synchronous.
If the primary database is lost, the synchronous replica becomes the primary database, the asynchronous replica becomes the synchronous replica.
Elasticsearch for search
Since, among other things, CB is also an instant messenger, we need a quick, convenient and flexible search, taking into account the morphology, by inaccurate correspondences. We decided not to reinvent the wheel and use the free search engine Elasticsearch, based on the Lucene library . We also expand Elasticsearch in a cluster (master - data - data) to eliminate problems in case of failure of application nodes.
On github, we found a Russian morphology plugin for Elasticsearch and use it. In the Elasticsearch index, we store the roots of the words (which the plugin defines) and the N-grams. As the user enters the text for the search, we are looking for typed text among N-grams. When you save to the index, the word "texts" is divided into the following N-grams:
[those, tech, tex, text, texts, ek, ex, exts, exts, ks, ksts, cpsy, art, shty, you],
And also the root of the word "text" will be saved. This approach allows you to search and at the beginning, and in the middle, and at the end of the word.
Overall picture

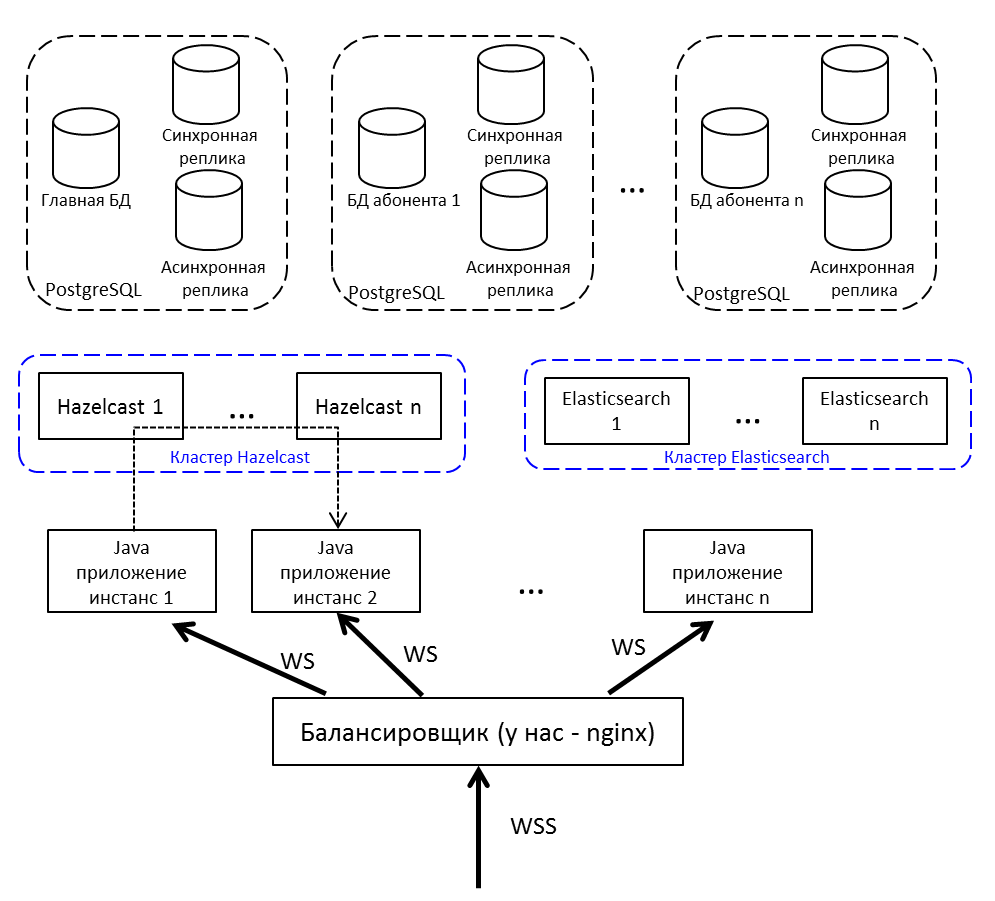
Repeat pictures from the beginning of the article, but with explanations:
- Online balancer; we have nginx, maybe any.
- Java application instances communicate via Hazelcast.
- For work with a web socket we use Netty .
- Java application written in Java 8, consists of OSGi bundles . The plans - migration to Java 10 and the transition to modules.
Development and Testing
During the development and testing of CB, we encountered a number of interesting features of the products used by us.
Load Testing and Memory Leaks
The release of each CB release is load testing. It was successful when:
- The test worked for several days and there were no service failures.
- Response time for key operations did not exceed the comfortable threshold
- The performance degradation compared with the previous version is not more than 10%
We fill the test database with data - to do this, we receive information from the production server about the most active subscriber, multiply its numbers by 5 (the number of messages, discussions, users) and so we test.
We carry out load testing of the interaction system in three configurations:
- Stress test
- Connections only
- Subscribers Registration
In the stress test, we run several hundred threads, and those without stopping load the system: write messages, create discussions, get a list of messages. We simulate the actions of ordinary users (get a list of my unread messages, write to someone) and software solutions (send a package of another configuration, handle the alert).
For example, this is how a part of the stress test looks like:
- User is logging in
- Requests his unread discussions
- With a 50% chance of reading messages
- 50% likely to write messages
- Next user:
- With 20% probability creates a new discussion.
- Randomly selects any of his discussions.
- Goes inside
- Requests messages, user profiles
- Creates five messages addressed to random users from this thread.
- Out of the discussion
- Repeats 20 times
- Log out, go back to the beginning of the script.
- A chat bot enters the system (emulates the exchange of messages from application code)
- With a 50% chance of creating a new channel for data exchange (special discussion)
- With a 50% chance of writing a message in any of the existing channels
The “Only Connections” scenario did not appear for nothing. There is a situation: users have connected the system, but have not yet been involved. Each user at 09:00 in the morning turns on the computer, establishes a connection with the server and is silent. These guys are dangerous, there are many of them - from the packages they have only PING / PONG, but they keep the connection to the server (they can't keep it - and what if a new message). The test reproduces the situation when in half an hour a large number of such users try to log in to the system. It looks like a stress test, but the focus is on this first entry - so that there are no failures (the person does not use the system, and it already falls off - it’s hard to think of something worse).
The subscriber registration script originates from the first launch. We conducted a stress test and were confident that the system does not slow down in correspondence. But users went and started to fall off registration by timeout. During registration, we used / dev / random , which is tied to the entropy of the system. The server did not have time to save enough entropy, and when it requested a new SecureRandom it would freeze for tens of seconds. There are many ways out of this situation, for example: switch to a less secure / dev / urandom, put a special fee that forms entropy, generate random numbers in advance and store in a pool. We have temporarily closed the problem with a pool, but since then we have run a separate test for registering new subscribers.
We use JMeter as a load generator.. He doesn’t know how to work with a web-application; we need a plugin. The first in search results for the query “jmeter websocket” are articles from BlazeMeter , which recommend a plugin from Maciej Zaleski .
We decided to start with it.
Almost immediately after the start of serious testing, we discovered that memory leaks started in JMeter.
The plugin is a separate big story, with 176 stars it has 132 forks on github. The author himself does not commit it since 2015 (we took it in 2015, then it did not arouse suspicion), several github issues about memory leaks, 7 unclosed pull request-s.
If you decide to do load testing with this plugin, pay attention to the following discussions:
- In a multi-threaded environment, the usual LinkedList was used, as a result, NPEs were obtained in runtime. It is solved either by switching to ConcurrentLinkedDeque, or by synchronized blocks. For myself, we chose the first option ( https://github.com/maciejzaleski/JMeter-WebSocketSampler/issues/43 ).
- Memory leak, disconnect does not remove connection information ( https://github.com/maciejzaleski/JMeter-WebSocketSampler/issues/44 ).
- In streaming mode (when the web socket does not close at the end of the sample, but used further in the plan) Response patterns do not work ( https://github.com/maciejzaleski/JMeter-WebSocketSampler/issues/19 ).
This is one of those on github. What we did:
- They took the fork of Elyran Kogan (@elyrank) - it fixed problems 1 and 3
- Solved problem 2
- Updated jetty from 9.2.14 to 9.3.12
- Wrapped SimpleDateFormat into ThreadLocal; SimpleDateFormat is not thread safe, resulting in NPE in runtime
- Eliminate another memory leak (connection was not properly closed during disconnect)
And yet it flows!
Memory began to end not in a day, but in two. There was no time left, we decided to run fewer threads, but on four agents. This should have been enough for at least a week.
Two days passed ...
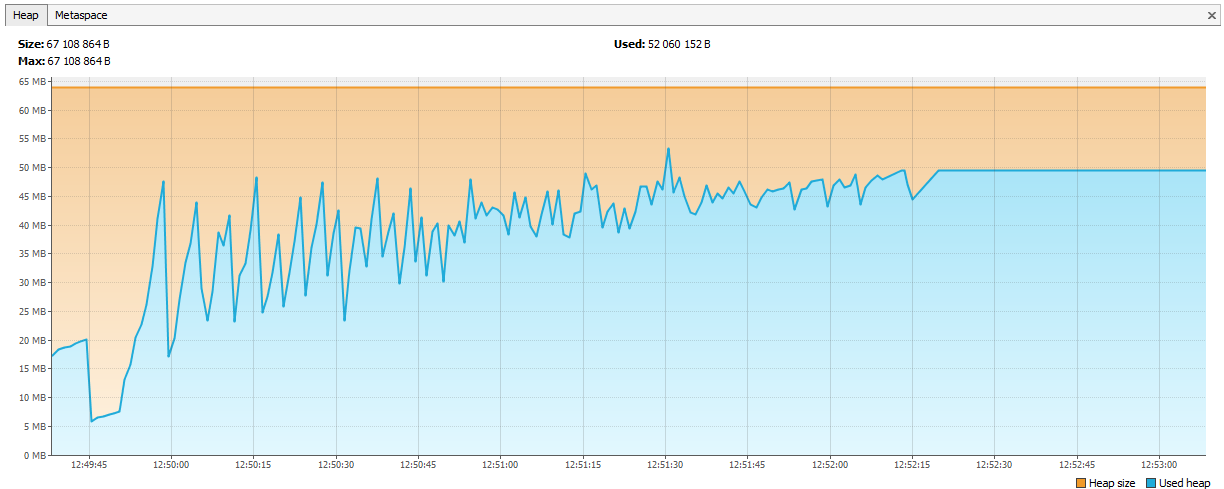
Now the memory began to end with Hazelcast. In the logs, it was clear that after a couple of days of testing, Hazelcast begins to complain about the lack of memory, and after some time the cluster falls apart, and the nodes continue to die one by one. We connected JVisualVM to the hazelcast and saw the “ascending saw” - he regularly called the GC, but could not clear the memory.

It turned out that in hazelcast 3.4 when deleting map / multiMap (map.destroy ()) the memory is not completely freed:
github.com/hazelcast/hazelcast/issues/6317
github.com/hazelcast/hazelcast/issues/4888
Now the bug is fixed in 3.5, but then it was a problem. We created new multiMap with dynamic names and deleted it according to our logic. The code looked like this:
publicvoidjoin(Authentication auth, String sub){
MultiMap<UUID, Authentication> sessions = instance.getMultiMap(sub);
sessions.put(auth.getUserId(), auth);
}
publicvoidleave(Authentication auth, String sub){
MultiMap<UUID, Authentication> sessions = instance.getMultiMap(sub);
sessions.remove(auth.getUserId(), auth);
if (sessions.size() == 0) {
sessions.destroy();
}
}Call:
service.join(auth1, "НОВЫЕ_СООБЩЕНИЯ_В_ОБСУЖДЕНИИ_UUID1");
service.join(auth2, "НОВЫЕ_СООБЩЕНИЯ_В_ОБСУЖДЕНИИ_UUID1");MultiMap was created for each subscription and was deleted when it was not needed. We decided that we will start Map <String, Set>, the key will be the name of the subscription, and the identifiers of the sessions as values (which can then be used to get user IDs, if necessary).
publicvoidjoin(Authentication auth, String sub){
addValueToMap(sub, auth.getSessionId());
}
publicvoidleave(Authentication auth, String sub){
removeValueFromMap(sub, auth.getSessionId());
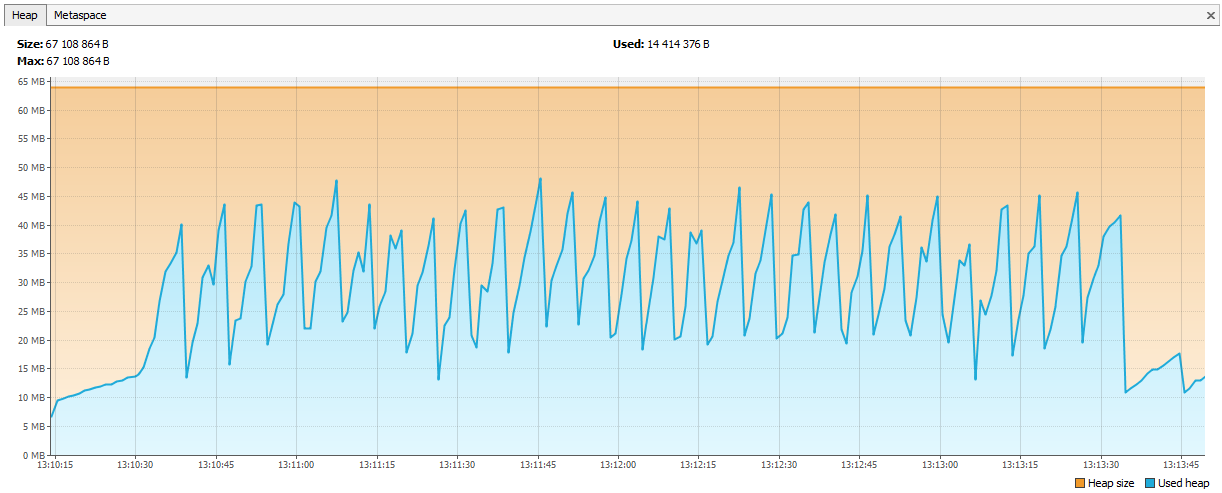
}The charts straightened.

What else have we learned about load testing?
- JSR223 needs to be written on groovy and include compilation cache - it is much faster. Link .
- Jmeter-Plugins graphics are easier to understand than standard ones. Link .
About our experience with Hazelcast
Hazelcast for us was a new product, we started working with it from version 3.4.1, now version 3.9.2 is on our production server (at the time of this writing, the latest version of Hazelcast is 3.10).
ID generation
We started with integer ids. Let's imagine that we need another Long for a new entity. Sequence in DB is not suitable, tables participate in sharding - it turns out that there is a message ID = 1 in DB1 and a message ID = 1 in DB2, in Elasticsearch you can’t put it on this ID, in Hazelcast too, but the worst thing is if you want to reduce the data from two databases to one (for example, deciding that one base is enough for these subscribers). You can start several AtomicLongs in Hazelcast and keep the counter there, then the performance of getting a new ID is incrementAndGet plus the time for a query in Hazelcast. But in Hazelcast there is something more optimal - FlakeIdGenerator. Each client is issued with a range of IDs, for example, the first is from 1 to 10,000, the second is from 10,001 to 20,000, and so on. Now the client can issue new identifiers independently, until the range given to him ends. It works quickly, but when the application is restarted (and the Hazelcast client), a new sequence begins - hence omissions, etc. In addition, developers are not very clear why the ID is an integer, but they are so much at odds. We all weighed and switched to UUIDs.
By the way, for those who want to be like Twitter, there is such a Snowcast library - this is the implementation of Snowflake on top of Hazelcast. You can see it here:
github.com/noctarius/snowcast
github.com/twitter/snowflake
But we have not reached our hands.
TransactionalMap.replace
Another surprise: TransactionalMap.replace is not working. Here is a test:
@TestpublicvoidreplaceInMap_putsAndGetsInsideTransaction(){
hazelcastInstance.executeTransaction(context -> {
HazelcastTransactionContextHolder.setContext(context);
try {
context.getMap("map").put("key", "oldValue");
context.getMap("map").replace("key", "oldValue", "newValue");
String value = (String) context.getMap("map").get("key");
assertEquals("newValue", value);
returnnull;
} finally {
HazelcastTransactionContextHolder.clearContext();
}
});
}
Expected : newValue
Actual : oldValueI had to write my replace using getForUpdate:
protected <K,V> booleanreplaceInMap(String mapName, K key, V oldValue, V newValue){
TransactionalTaskContext context = HazelcastTransactionContextHolder.getContext();
if (context != null) {
log.trace("[CACHE] Replacing value in a transactional map");
TransactionalMap<K, V> map = context.getMap(mapName);
V value = map.getForUpdate(key);
if (oldValue.equals(value)) {
map.put(key, newValue);
returntrue;
}
returnfalse;
}
log.trace("[CACHE] Replacing value in a not transactional map");
IMap<K, V> map = hazelcastInstance.getMap(mapName);
return map.replace(key, oldValue, newValue);
}Test not only regular data structures, but also their transactional versions. It happens that IMap works, and TransactionalMap is no longer there.
Put a new JAR without downtime
At first we decided to record objects of our classes in Hazelcast. For example, we have an Application class, we want to save and read it. Save:
IMap<UUID, Application> map = hazelcastInstance.getMap("application");
map.set(id, application);We read:
IMap<UUID, Application> map = hazelcastInstance.getMap("application");
return map.get(id);Everything is working. Then we decided to build an index in Hazelcast, to look for it:
map.addIndex("subscriberId", false);And when writing a new entity, we started getting ClassNotFoundException. Hazelcast tried to supplement the index, but knew nothing about our class and wanted to have a JAR planted with this class. We did it, it all worked, but a new problem appeared: how to update the JAR without completely stopping the cluster? Hazelcast does not pick up a new JAR with a new update. At this point, we decided that we could live without index search. After all, if you use Hazelcast as a key-value type storage, then everything will work? Not really. Here again the different behavior of IMap and TransactionalMap. Where IMap doesn't care, TransactionalMap throws an error.
IMap. We write down 5000 objects, we read. Everything is expected.
@Testvoidget5000(){
IMap<UUID, Application> map = hazelcastInstance.getMap("application");
UUID subscriberId = UUID.randomUUID();
for (int i = 0; i < 5000; i++) {
UUID id = UUID.randomUUID();
String title = RandomStringUtils.random(5);
Application application = new Application(id, title, subscriberId);
map.set(id, application);
Application retrieved = map.get(id);
assertEquals(id, retrieved.getId());
}
}And in the transaction does not work, we get a ClassNotFoundException:
@Testvoidget_transaction(){
IMap<UUID, Application> map = hazelcastInstance.getMap("application_t");
UUID subscriberId = UUID.randomUUID();
UUID id = UUID.randomUUID();
Application application = new Application(id, "qwer", subscriberId);
map.set(id, application);
Application retrievedOutside = map.get(id);
assertEquals(id, retrievedOutside.getId());
hazelcastInstance.executeTransaction(context -> {
HazelcastTransactionContextHolder.setContext(context);
try {
TransactionalMap<UUID, Application> transactionalMap = context.getMap("application_t");
Application retrievedInside = transactionalMap.get(id);
assertEquals(id, retrievedInside.getId());
returnnull;
} finally {
HazelcastTransactionContextHolder.clearContext();
}
});
}In 3.8, the User Class Deployment mechanism appeared. You can assign one master node and update the JAR file on it.
Now we have completely changed the approach: we serialize ourselves into JSON and save to Hazelcast. Hazelcast does not need to know the structure of our classes, and we can be updated without downtime. Versioning of domain objects is controlled by the application. At the same time, different versions of the application can be launched, and it is possible that a new application writes objects with new fields, but the old one does not know about these fields. And at the same time, the new application reads objects written by the old application, in which there are no new fields. We handle such situations inside the application, but for simplicity we do not change or delete fields, we only expand classes by adding new fields.
How we provide high performance
Four trips to Hazelcast - good, two trips in the database - bad
Going for data in the cache is always better than in the database, but you do not want to store unclaimed records either. The decision that to cache, we postpone for the last stage of development. When the new functionality is encoded, we enable logging of all requests (log_min_duration_statement to 0) in PostgreSQL and run load testing for 20 minutes. Using the collected logs, utilities like pgFouine and pgBadger can build analytical reports. In the reports we are primarily looking for slow and frequent requests. For slow queries, we build an execution plan (EXPLAIN) and evaluate whether such a query can be accelerated. Frequent requests for the same input data fit well into the cache. We try to keep the requests “flat”, one table in the request.
Exploitation
SV as an online service was launched in the spring of 2017, as a separate SV product was released in November 2017 (at that time in beta status).
For more than a year of operation, there were no serious problems with the operation of the SV online service. Online service is monitored via Zabbix , assembled and deployed from Bamboo .
The CB distribution package is delivered in the form of native packages: RPM, DEB, MSI. Plus for Windows, we provide a single installer in the form of a single EXE, which installs the server, Hazelcast and Elasticsearch on one machine. At first we called this version of the installation “demo”, but now it has become clear that this is the most popular deployment option.
