"Dormamma, I came to agree": an algorithm for mutually beneficial cooperation with a person

Reflections on the topic of artificial intelligence have been visiting the minds of great people for many centuries. With the passage of time and the development of technology, reflections turned into realization, theories into practice, and science fiction into the very real future of humanity. The main essence of AI is helping a person. In other words, smart machines should serve man in full men, without violating the fundamental laws of robotics, which the well-known Isaac Asimov said. But such an interaction, if we talk on the ground, has only one vector: the person said - the AI performed. That is, the work of artificial intelligence is aimed at the benefit of only man. But what if the AI thinks in line with the good for both sides of the interaction? How to teach a car to find a compromise, to negotiate and even bargain with a person? Well, These questions are answered by today's research, in which an algorithm was created that allows the machine to reach a mutually beneficial agreement with a person. Let's take a closer look at these questions. Go.
The idea of the study
Researchers note that ever since Turing started talking about artificial intelligence, a person has been trying to create a machine capable of surpassing it in some way. All of us are somehow familiar with numerous contests, competitions and experiments when a person competes with a machine (chess, poker and even martial arts). However, until now, very little attention was paid to a different kind of interaction between man and machine. After all, it is not always in life that there is only victory or defeat. Sometimes we need the very consensus when the needs and / or desires of the two parties are satisfied.
To consider the work of AI solely from the point of view of “yes or no” is wrong, because there is always the option “probably.”
Scientists managed to create an algorithm that is able to assess the situation, weigh the pros and cons, distribute priorities and reach a compromise. To test the algorithm, repeated stochastic games * were used .
A stochastic game * is a repetitive game with one or more players when its state is constantly changing in random order.Creating an algorithm that can work in such “floating” conditions is not an easy task. In order to work effectively, the algorithm must have some features. Further details about them.
Firstly, the algorithm should not be domain-specific, that is, it should work in an unlimited number of scenarios (in this case, games). This feature is called "universality" by scientists.
Secondly, the algorithm must learn to build successful connections with any people / algorithms without prior knowledge of their behavior. This is "flexibility." To achieve this, the algorithm must take into account that its opponent partner almost always adheres to its operational behavior, that is, it wants to use the algorithm exclusively for its own benefit. As a result, it must determine when and how to involve in cooperation one who most likely does not intend to cooperate.
And finally, thirdly, the algorithm must act quickly, especially when playing with a person. This feature is called "learning speed".
In words, everything is very beautiful, clear and simple. In fact, the achievement of such characteristics is fraught with difficulties. Not to mention the fact that the ability to adapt to an opponent may be complicated by the fact that the opponent himself is able to adapt. This is a problem, since the two adaptive algorithms, despite all their attempts to adapt to each other, cannot reach a compromise.
Also, scientists note that during the interaction between two people, some of the important tools for achieving mutually beneficial results are things that are difficult to associate with the machine, these are intuition, emotions, instincts, and so on. It has been proven that “cheap talk” is strongly associated with a mutually beneficial outcome.
Cheap Talk (cheap talk) * - in game theory, this is an interaction between players that does not directly affect the outcome of the game. In other words, "talking off topic."The researchers decided to incorporate this into their algorithm, which helps him better cope with the calculations of complex situations and develop a common understanding of the situation with a person. Although it is still not entirely clear how the algorithm will implement such “skills” in conjunction with its main features (flexibility, universality, learning speed).
The main task of the study is to study as many existing algorithms as possible, develop an algorithm based on machine learning with a mechanism for responding to signals and generating them at a level understandable to humans, and also conduct a lot of experimental game games to demonstrate the learning ability of the algorithm and its ability to adapt to different opponents (people or other algorithms).
Conducting and results of the study
Algorithms of strategic behavior in repetitive games are present in many aspects of society: economics, evolutionary biology, AI, etc. At the moment, many such algorithms have been created, each of which has its own set of advantages. Naturally, scientists decided to use them to develop their own algorithm. Thus, 25 algorithms were selected.
It was allocated 6 performance indicators based on three variants of the game: 100, 1000 and 50,000 rounds.
Performance Indicators:
- average round-robin * ;
- best score on points;
- worst score on points;
- replicator dynamics * ;
- tournament group-1;
- tournament group-2.
Round-Robin * is a type of game interaction, when during a round each participant alternately plays with all other participants.
Replicator Equation * is a deterministic monotone nonlinear game dynamics used in evolutionary game theory.The first indicator (the average value of Round-Robin) allows you to understand how well the algorithm is able to establish beneficial relationships with various game partners.
The second indicator (the best result in points) is the number of partner algorithms, in the game with which the algorithm studied earned the highest number of points. Expressed as a percentage. This indicator shows how often the algorithm will be the desired choice, given the information about the algorithm of the partner in the game.
The third indicator (the worst result on points) is the assessment of the ability of the algorithm to link its losses (misses, errors).
The remaining three indicators are aimed at determining the stability of the algorithm for different groups of the population.
For example, a tournament (group-1) is a series of games in which the algorithms are divided into 4 groups. Leaders from each group go to the final, where the only winner is determined. But in the group 2 tournament, two best algorithms are selected from each group, which go into the semi-finals, and then the winners go to the final, where the only best algorithm is determined.
According to scientists, none of the selected algorithms (25 pieces) had previously participated in such a large-scale verification (many partners and measured indicators). Such a check shows how well each of the algorithms works in a normal game with 2 participants, and is not “programmed” for a particular scenario.

Table 1: the results of experiments involving 25 different algorithms of strategic behavior.
The results are only a tool that allows you to better understand the pros and cons of an algorithm. For example, gTFT, WSLS, Mem-1 and Mem-2 algorithms showed excellent results in the prisoner's “dilemma” * .
Prisoner's dilemma * - in game theory, a state where players are not always ready to cooperate, even if it is to their advantage. In this case, the player (“prisoner”) has his own interests in priority, and he does not think about the benefits of others.However, the same algorithms showed poor results in all 2x2 games, which indicates their inefficiency in longer interactions. Consequently, they cannot adapt to the behavior of a partner (another player).
Another amusing observation was the fact that the Exp3, GIGA-WoLF and WMA algorithms, which are the basis for the algorithms of the world poker championship, also showed a bad result. Which is quite obvious, because the "poker" algorithm should not cooperate with other players, but to excel and defeat them.
If we consider all the indicators as a whole, then one algorithm stands out - S ++, which showed itself perfectly in all types of games with all possible checked combinations. In addition, it is worth noting that for most algorithms, the development of cooperation behavior took place only after thousands of rounds. For S ++, this process took only a few rounds, which makes it an excellent option, given the importance of this indicator in a game involving not an algorithm, but a living person. The faster the algorithm “realizes” the necessity and advantage of cooperation and compromise, the easier and faster it will be able to achieve it.
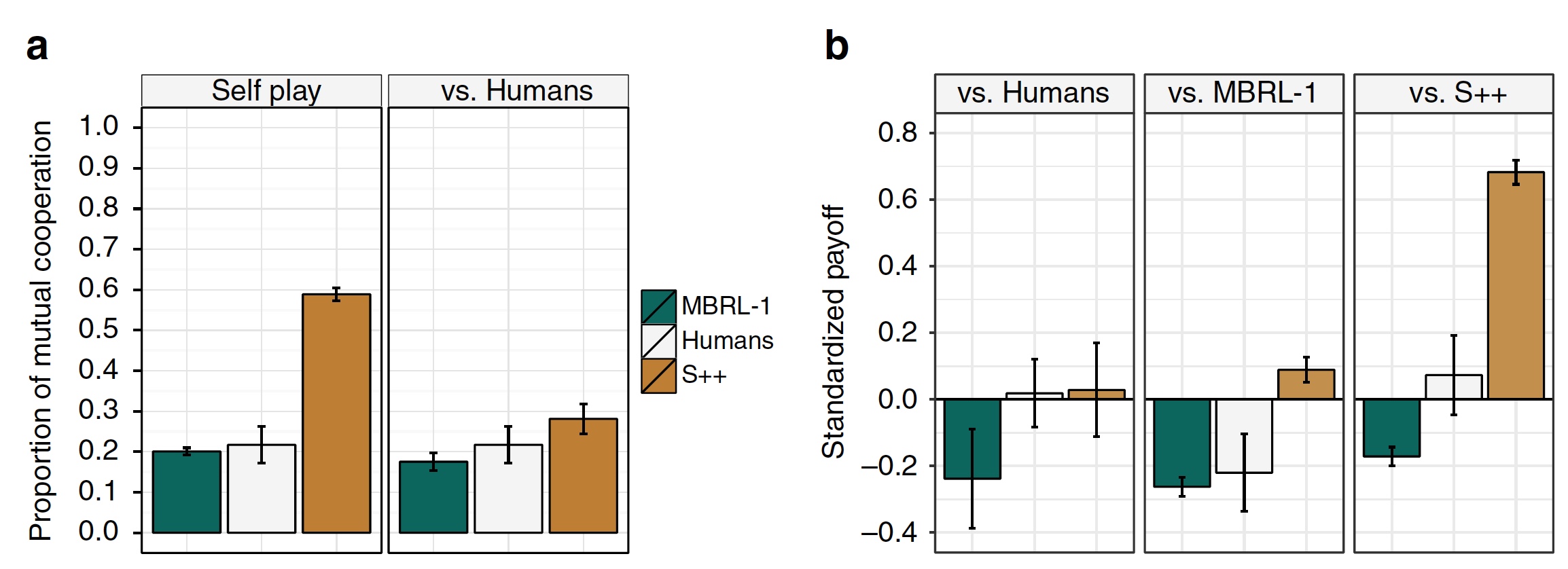
The results of the experiment "S ++ against man."
The interaction of S ++ with other algorithms showed a good result, therefore, it was necessary to check how S ++ will behave when working with real people.
In the experiment (4 repeating games of 50 or more rounds), S ++ and MBRL-1 algorithms, as well as a group of people, participated. The results of this experience are visible in the graphs above. We see that the establishment of cooperation of S ++ with its copy is excellent, but with people this process is not consistent. Moreover, S ++ managed to achieve long-term cooperation with a person only in <30% rounds. Not the most encouraging result, but people playing with people also failed to establish long-lasting cooperation.
Although S ++ was distinguished from other algorithms, it did not allow him to become the clear winner in this study. None of the 25 algorithms could not demonstrate the ability to build long-term cooperative relationships with a human player.
S #: human cooperative and algorithm
As mentioned earlier, such an aspect as “cheap talk” plays an important role in achieving long-term cooperation between the parties, however, such a technique has not been previously implemented in any of the above games. Therefore, the scientists decided to create their own version, which will allow players to use this technique, but to a limited extent - 1 message at the beginning of each round.
For a person, such conversations are natural. However, for a machine that is focused on solving a problem and will do for this, what is logical, such forms of interaction are alien. The idea of introducing such behavior directly leads scientists to the notion of “Explainable AI” (“explicable AI”), when the actions of a machine are easily understood by a person. The problem is that most of the algorithms based on machine learning have a low-level internal representation, which is difficult to express at a level that is understandable for humans.
Fortunately, the internal structure of S ++ has a very high level, which allows it to be used as a basis for introducing the “cheap talk” technique. In S ++, a communication framework was introduced that allows generating and responding to “cheap conversations”.
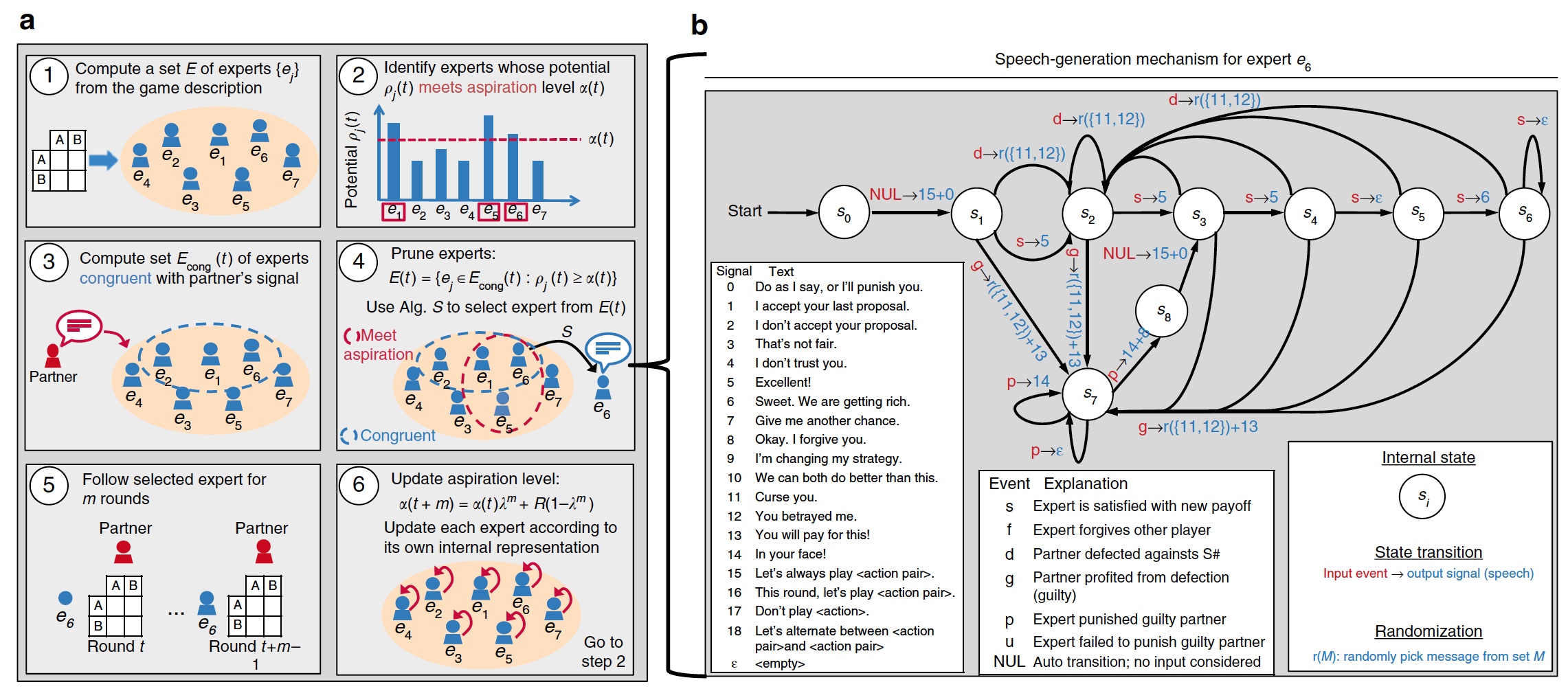
The new form of the S ++ algorithm was called S #.
The image (a) shows the scheme of the algorithm, and (b ) shows the scheme of interaction with a game partner using the “cheap talk” technique. Also on b we can get acquainted with the variants of phrases that the S # algorithm can generate, and what answer it expects for a particular phrase.
Thus, S # is able to respond to the “signals” (phrases and actions) of the partner player, which allows him to decide which tactics to use next. Together with a high degree of self-learning of the original S ++ algorithm, the resulting algorithm can create long-term mutually beneficial relationships with the player, person, or another algorithm.
In order to verify this statement, the scientists organized an experiment involving 220 people. A total of 472 repetitive games were conducted. The “cheap talk” technique was also included in the experiment, but not always. And the personalities of the players were hidden, so no one (neither the algorithm nor the people) knew who they were playing with.
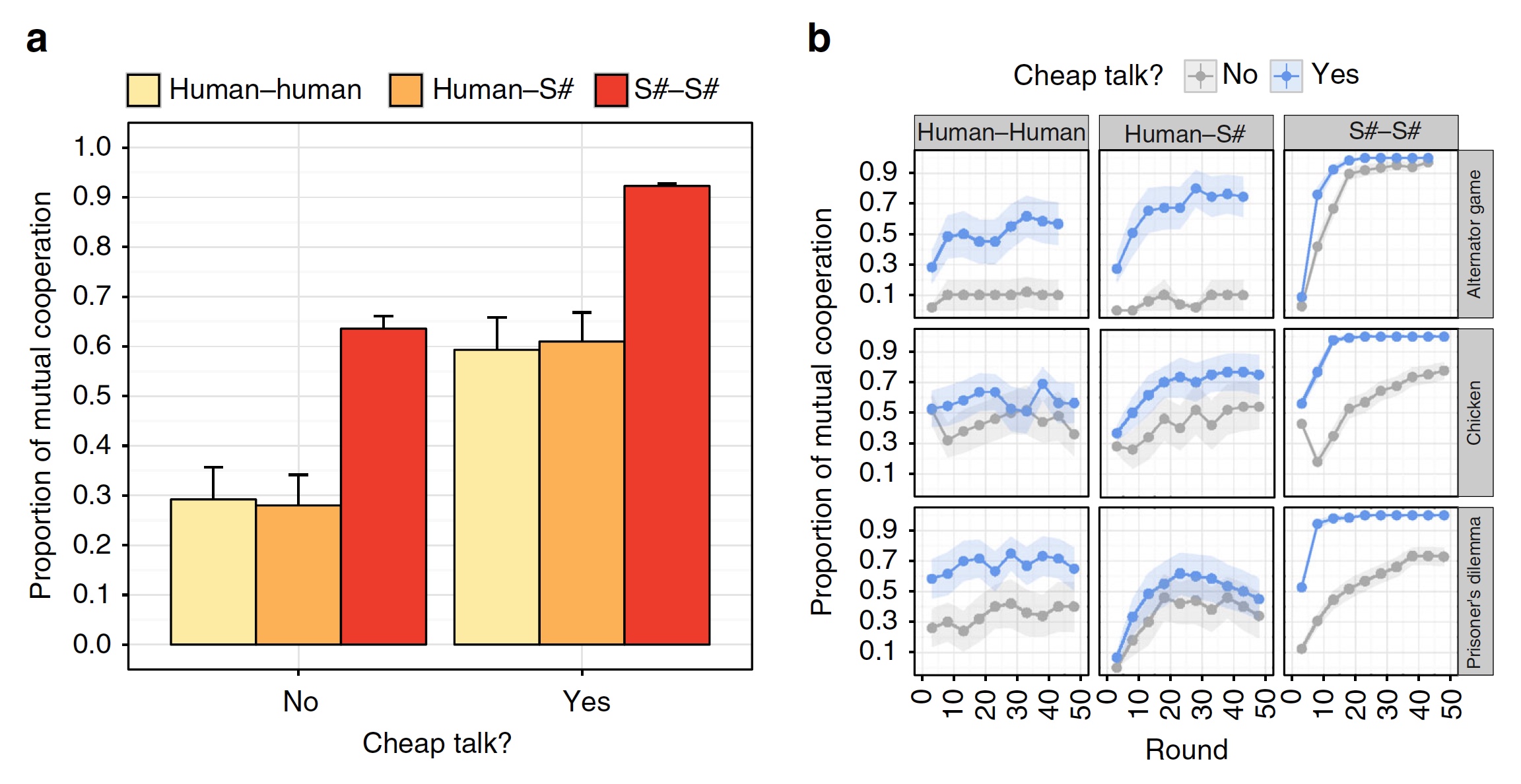
The results of the experiment with the participation of 220 people.
When “cheap talk” was not included in the game process, human-to-person or human-S # interaction did not lead to long-term cooperation. When this technique was included in the game, the indicators of cooperation will double.
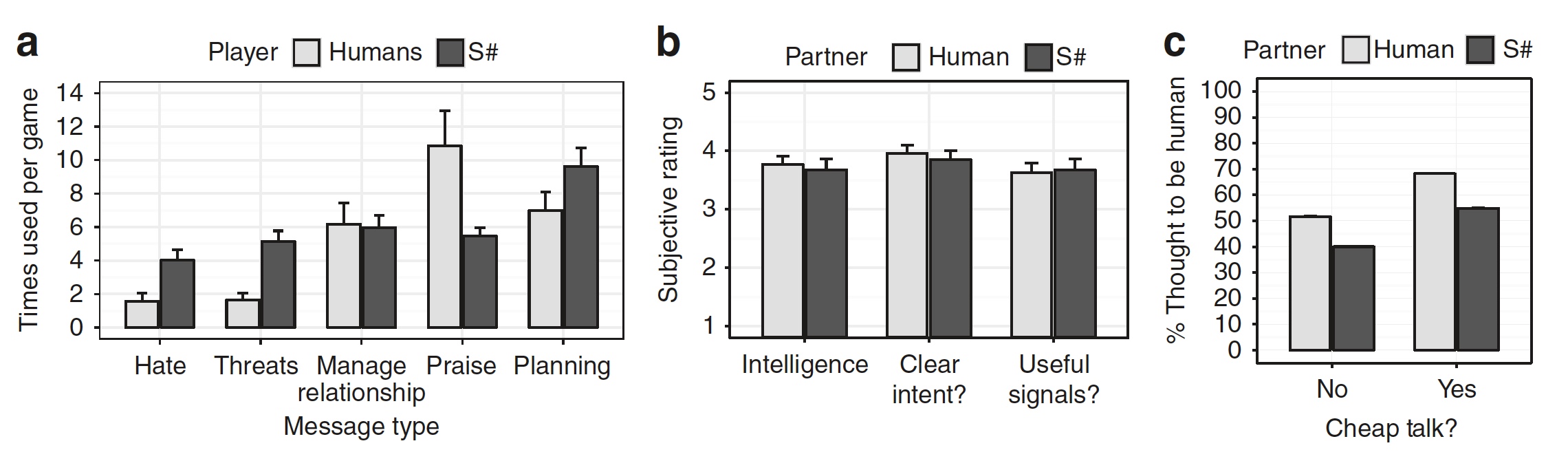
Graph (a) shows what kind of phrases were used during the game of a person and the S # algorithm (hate, threat, control, praise or planning).
After the experiment, all participants were asked to evaluate the intelligence level of their partners in the game, how clear their intentions and the usefulness of interaction with them were to them. The results of the survey on the graph (b) . Even more interesting is the schedule (s) . It shows the percentage of how many times a person or algorithm considered its partner in the game a person. As you can see, most of the people involved felt that S # was a human.
Scientists also point out that the results of S # become even better when compared with the way man-man and S # -S # pairs interacted. The degree of occurrence of long-term cooperative relations between a person and S # is about the same level as that of a man-to-person couple. And for a pair of S # -S #, without using the “cheap talk” technique, the result is significantly better than that of a pair of person-to-person who could use it.
Summarizing all the above, the S # algorithm showed results that can be set on the same level as the results of interaction between people.
Duplicate stochastic games
Normal type games made it possible to understand that the S # algorithm is a promising vector of research. However, these games are limited, they are more abstract. Therefore, the scientists decided to use a recurring stochastic game in which participants must share blocks of different shapes and colors. For the S # algorithm, the phrases “Let's cooperate” and “I get more points” were added. In addition, S # was limited to using the “cheap talk” technique - he could use phrases, but could not respond to phrases from a human player.
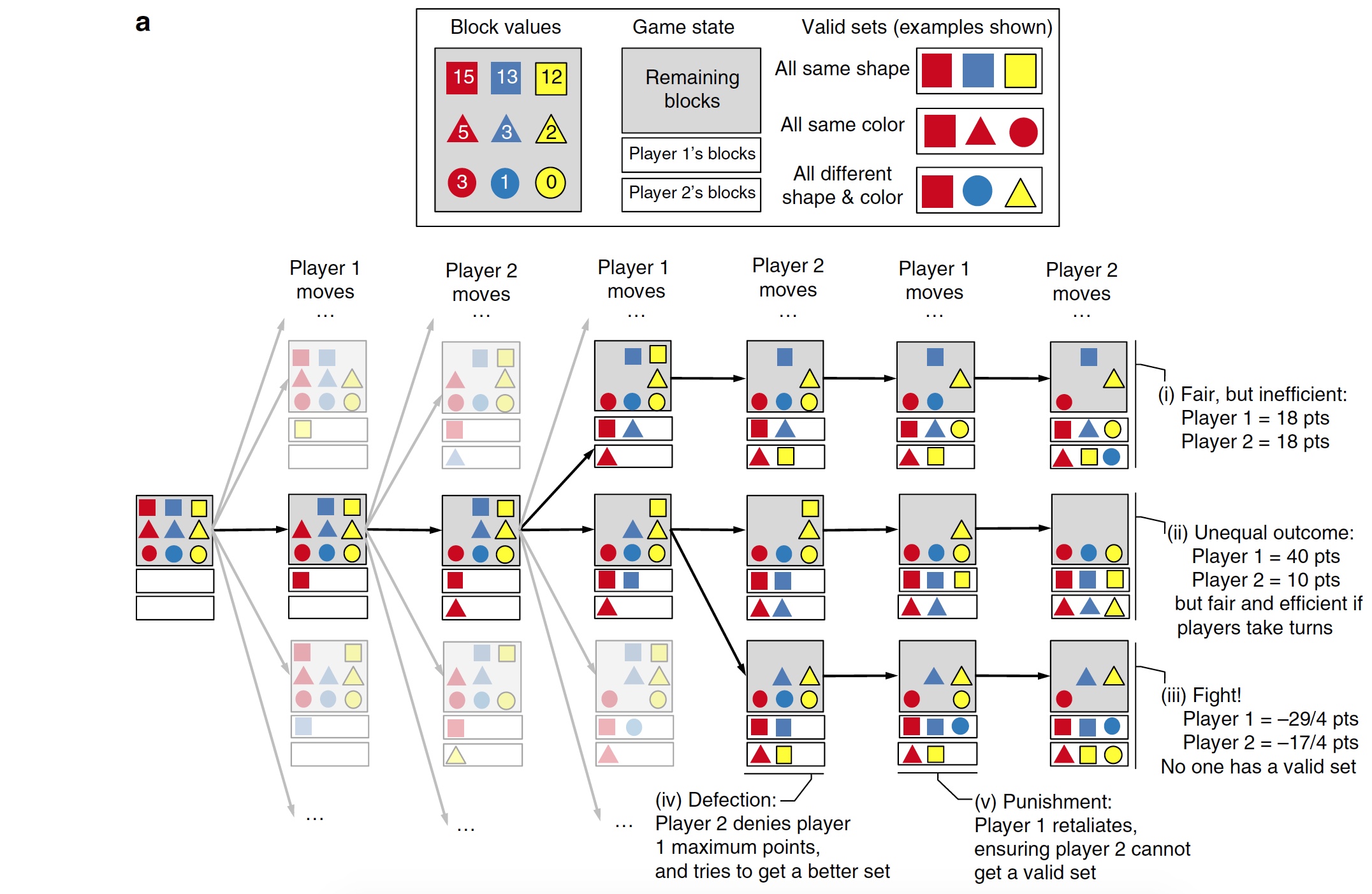
The scheme of the game with multi-colored blocks (square, circle and triangle).
The essence of the game is as follows. Each player has a set of 9 blocks (different, of course). Each turn, the player removes 1 block from his set until he has only 3. These three blocks must meet the requirements (the same shape / color or different shape and color at the same time). Each block is worth a certain number of points (points). If the block is unsuitable, then this number becomes negative. The diagram above shows 5 options for the outcome of the game.
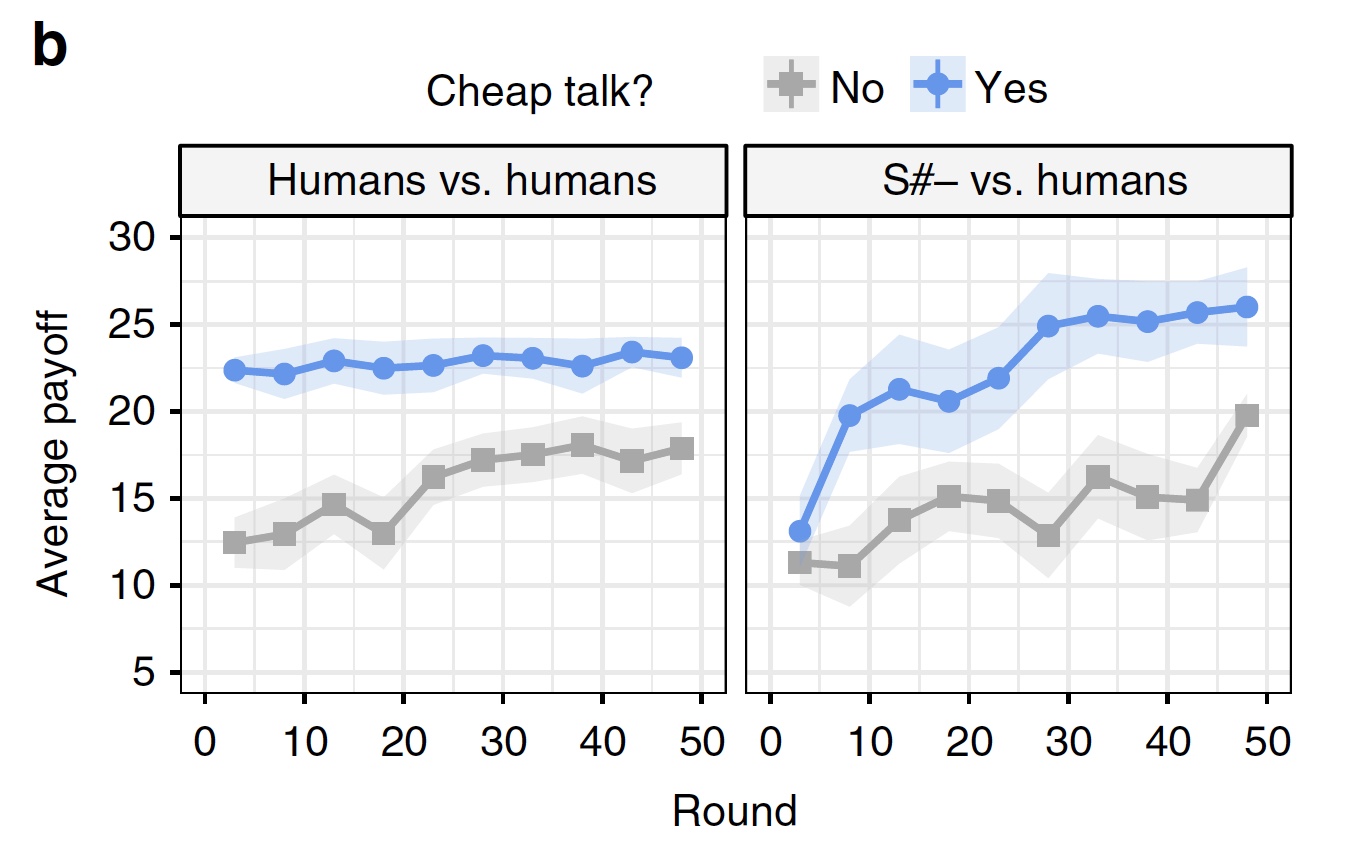
Using and not using “cheap talk”.
When playing between people, the use of “cheap conversations” did not greatly affect its outcome. However, this technique greatly increased the result of the S # algorithm in a game with a man.
Differences S # from other algorithms
The S # algorithm exceeded all other subjects, but why? What features of this algorithm distinguish it from a number of competitors? Scientists counted as many as three.
First, it is the ability to generate and respond to appropriate signals (phrases and actions) that can be understood by a person. This makes this algorithm very flexible, able to evolve depending on the situation. And, of course, allows you to form long-term mutually beneficial relationships with other players.
Secondly, S # uses a diverse set of strategies, which allows you to adapt to different partner partners and different types of games. At the same time, algorithms created to work efficiently in only one specific scenario cannot work effectively outside their “comfort zone”.
Thirdly, the S # algorithm supports the state of mutual benefit, while other algorithms, having received the desired, switch to another strategy.
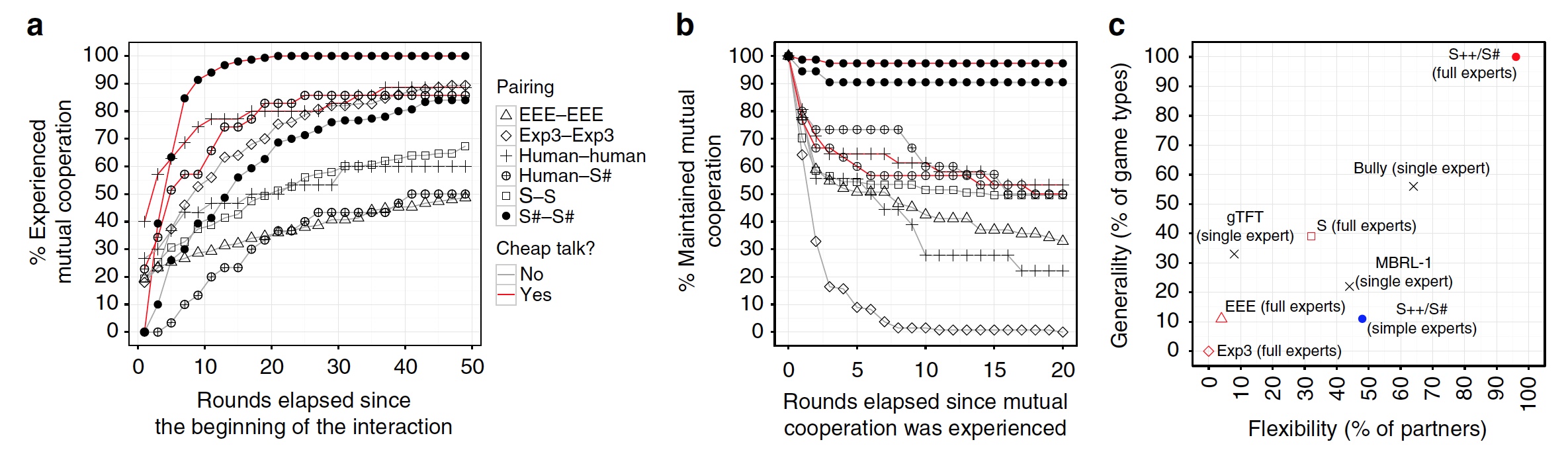
Graphs of the duration of the state of mutually beneficial cooperation.
As can be seen from the graph above (a) , S # establishes a mutually beneficial relationship with the player earlier than other algorithms. It also keeps the state of mutually beneficial cooperation, a much larger number of rounds than competing algorithms (chart (b) ).
The flexibility of S # is clearly visible from the graph (s) , where we see that it achieves a goal more often than others, regardless of the type of game or partner.
It is quite unusual for scientists to claim that their S # algorithm has learned fidelity. The fact is that by establishing cooperation in a pair of S # -S #, the algorithm is in no hurry to break it, even when there is no special benefit in this. While in pairs of person-to-person cooperation, often broke off immediately after reaching the necessary short-term benefit. This behavior naturally led to a deterioration in the results at the end of the game for both sides.
Those who wish to familiarize themselves with the report of scientists can find it here .
Additional research materials are available here .
Epilogue
This study is very different from others in that it is aimed not at creating an AI capable of defeating a person in something, but at creating an AI capable and willing to reach consensus. Does this mean that smart machines will become more humane thanks to this algorithm? Maybe. Indeed, despite all human stubbornness and vanity, we always try to find a common language, to establish a dialogue, the result of which will be beneficial to both parties.
Much remains to be understood and improved before the S # algorithm becomes a full-fledged "negotiator". But the potential is great, as is the enthusiasm of scientists. Let's hope that the result of their hard work will not make us wait long.
Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending to friends, 30% discount for Habr's users on a unique analogue of the entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to share the server? (Options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
3 months for free if you pay for new Dell R630 for half a year - 2 x Intel Deca-Core Xeon E5-2630 v4 / 128GB DDR4 / 4x1TB HDD or 2x240GB SSD / 1Gbps 10 TB - from $ 99.33 a month , only until the end of August, order can be here .
Dell R730xd 2 times cheaper?Only we have 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV from $ 249 in the Netherlands and the USA! Read about How to build an infrastructure building. class c using servers Dell R730xd E5-2650 v4 worth 9000 euros for a penny?
