Shortest Common Superstring Problem
The problem of the shortest common superline is formulated as follows: find the shortest line such that each line from the given set would be its substring. This problem occurs both in bioinformatics (the task of genome assembly in the general case) and in data compression (instead of data, store their superstructure and sequence of pairs, type (occurrence index, length)).
When I searched the Internet for information on this problem and its solution in Russian, there were only a couple of posts about bioinformatics, where these words are mentioned in passing. Of course, there was no code (except for the greedy algorithm). Having understood the problem, this fact has been advanced to an article here.
Caution, 4 megabytes!
For the most part, the article is an attempt to translate into an understandable language, illustrate, season with an example, and, of course, implement in Java a 4-approximate algorithm for constructing a superline from Dan Gasfield's book (see the literature used). But first, a small introduction and a 2-approximate, greedy algorithm.
In the simplest case (if the name of the problem did not contain the word “shortest”), the solution to the problem would be to simply concatenate the input strings in random order. But in this formulation of the problem, we are dealing with NP-completeness, which means that at present there is no algorithm with which to solve this problem on a Turing machine in a time not exceeding the polynomial in data size.
Input: S 1 , S 2 , ..., Sn is the set of lines of the finite alphabet E *.
Conclusion: X is a string of the alphabet E * containing each string S 1..n as a substring, where the length | X | minimized.
Example. Take the set of lines S = {abc, cde, eab}. In the case of concatenation, the length of the output superline will be 9 (X = abccdeeab), which is obviously not the best option, since lines can have a suffix-prefix match. The length of this match will be called overlap . (The choice of the English word was not accidental, since it does not have a specific and unambiguous translation into Russian. In Russian-language literature, the terms overlap, intersection, overlap and suffix-prefix match are usually used).
Retreat.The concept of overlap is one of the most important in the process of implementing algorithms for constructing add-ins. The calculation of overlap for an ordered pair of strings (S i , S j ) is reduced to finding the length of the maximum match of the suffix of the string S i with the prefix of the string S j .

One way to program to find overlap is presented in the following listing.
Return for example. If we concatenate the strings S = {abc, cde, eab} taking into account their overlaps, we get the string X = abcdeab with a length of 7, which is shorter than the previous one, but not the shortest. The shortest string will be obtained when concatenating strings with overlaps in the order of 3-1-2, then the resulting string X = eabcde will have a length of 6. Thus, we reduced the problem to finding the optimal order of concatenating strings taking into account their overlaps.
Restriction. All existing algorithms for finding the shortest superstructures assume that no input set string is a substring of any other string. Deleting such lines can be done, for example, using the suffix tree and, obviously, does not detract from the generality.
In this algorithm, at each iteration, we try to find the maximum overlap of any two lines and merge them into one. We hope that the result of this algorithm will be close to the actually optimal one.
1. While S contains more than one line, we find two lines with the maximum overlap and merge them into one (for example, ABCD + CDEFG = ABCDEFG).
2. We return one line remaining in S.
An example implementation of this algorithm is presented in the following listing.
Another simple merge function appeared in this listing, which merges two lines into one, taking into account their overlap. Since the latter has already been calculated, it is logical to simply pass it as a parameter.
One example ( worst case ):
● Input : S = {“ab k ”, “b k c”, “b k + 1 ”}
● Output of the greedy algorithm: “ab k cb k + 1 ” with a length of 4 + 4k
● Conclusion of the optimal algorithm: “ab k + 1 c” with a length of 4 + 2k.
Approximation coefficient based on the worst case.
Generally speaking, this algorithm has no name and no one calls it like me. It is simply called a 4-approximate algorithm for constructing the shortest superline. But since Blum, Young, Lee, Tromp and Yannakakis came up with it, why not give such a headline?
For clarity , during the analysis of the algorithm I will give an example of constructing a superline for the set S = {S 0 : “cde”, S 1 : “abc”, S 2 : “eab”, S 3 : “fgh”, S 4 : “ ghf ”, S 5 :“ hed ”} .
Main ideathe algorithm is to find coverage by cycles of minimum full length for a complete directional weighted graph whose vertices are rows of a given set and the edge weight from S i to S j is equal to overlap (S i , S j ) for all i, j.
Graph for our example (the vertices for visibility are signed by i instead of S i ):

In my implementation, I will represent this graph as an adjacency matrix , which will be formed in the banal manner shown in the following listing (in section 16.17 [1] D. Gasfield argues that the matrix can be formed more efficiently, but the way this matrix is generated does not affect the consideration of this algorithm).
For our example, the adjacency matrix will look like this:

After the adjacency matrix is constructed, it becomes necessary to find a covering by cycles of minimum full length. Such coverage can be found by reducing this problem to the “assignment problem”. So, the task was to find the full purpose of the maximum weight (as it turned out, this step of the algorithm takes dominant time). Faster and easier ([1] p.16.19.13) this destination can be found by the greedy method.
Greedy appointment ([1] p.16.19.13)
Input data: matrix A of size k × k.
Result: full assignment M.
It is possible to represent M in the code as an array (int [] M = new int [k]) and interpret the first part of instruction 2.2 as M [i] = j; since in the full assignment, each number from 0 to k occurs exactly once as the row index and exactly once as the column index.
An example of the full assignment calculation implementation is presented in the following listing.
Step-by-step calculation of the full assignment of the maximum weight by the greedy method for our example:

Now that the full assignment of the maximum weight has been calculated, it is necessary to calculate the coverage in cycles of the minimum total length. To do this, you need:
taking any (logical - zero) index of the full assignment as the beginning, put it in the loop, mark it used and see if its value is equal to the index of the beginning of the cycle? If so, end the cycle, put it in the cover of the cycles and start a new cycle, taking the first unlabeled element as the beginning. If not, take this value as an index and repeat the procedure until all elements are marked.
The representation of coverage by loops in memory can be organized as a list of row index lists.
Algorithm listing (assign - full assignment):
For our example, finding coverage by loops will look like this:
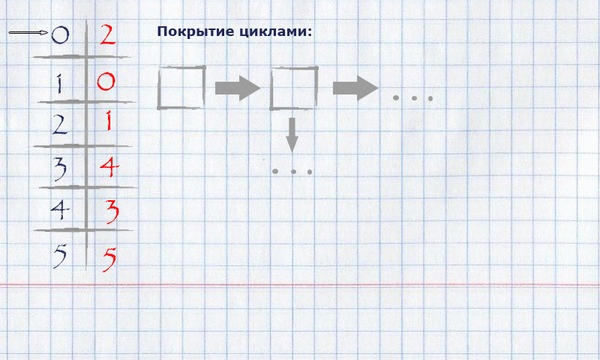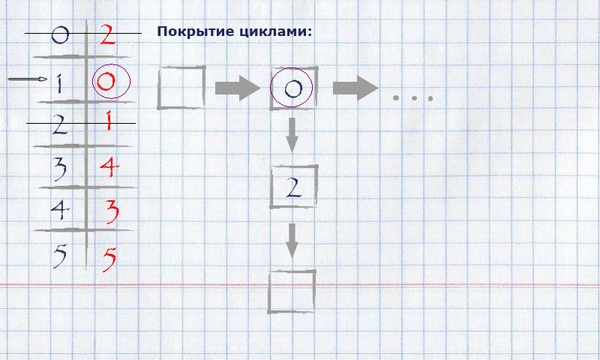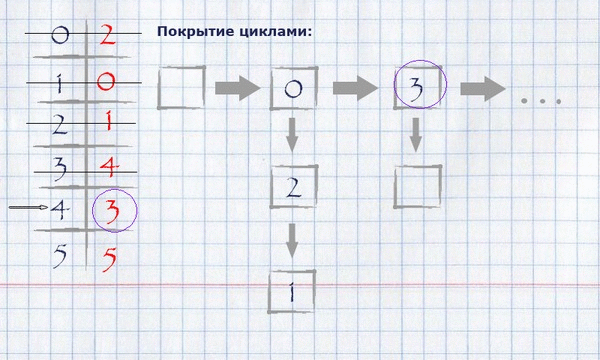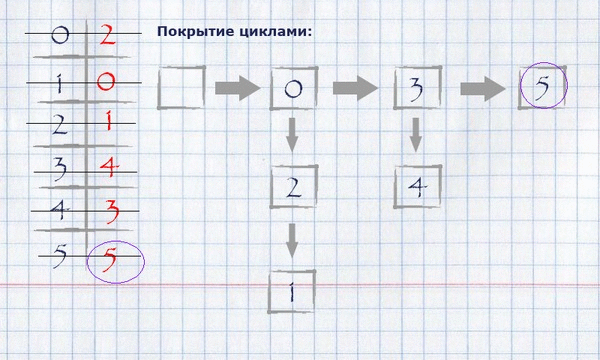
The resulting coverage in cycles can be displayed on the original graph, leaving only those edges that fell into the coverage.

Assembly. Now that all the cycles in the coverage have been calculated, you can start assembling, directly, the superstructure.
To do this, you need the prefix function, which takes the strings S 1 and S 2 and returns the string S 1 cut off to the right by overlap (S 1 , S 2 ) characters. But since all overlaps were counted by us for a long time, the function can be written so that it takes only one line and the number of characters by which it needs to be shortened.
Now, for each cycle C i = {S 1 , S 2 , ..., S k-1 , S k }, it is necessary to compose the sub-line X Ci = prefix (S 1 , overlap (S 1 , S 2 )) ++ prefix (S 2 , overlap (S 2 , S ...)) ++ prefix (S ..., overlap (S ..., S k-1 )) ++ S k .
The problem is that, since loops in a coverage are loops , it means we can twist them cyclically and it is not clear which line to start constructing an X Ci superstructure with . The answer is simple - you need to shift the cycle so thatminimize overlap of the last and first line.
Consider the first cycle of cyclic coating from the example.

If you do not minimize the overlap of the last and first lines, but take C 0 = {1, 0, 2}, then the line will be X C0 = abc ++ cde ++ eab = abcdeab, which is obviously not the shortest possible. The minimum overlap in this loop is 1, which means that any of the sequences {0, 2, 1} (cde ++ eab ++ abc = cdeabc) or {2, 1, 0} (eab ++ abc ++ cde = eabcde).
The following is a code that cyclically shifts each cycle in the coverage so as to minimize overlap of the first and last lines of each cycle, and constructs add-ins for each cycle.
We now have the shortest add-ins for each cycle in the coverage. The considered algorithm with a factor of 4 assumes a simple concatenation of these lines.
The source codes for the greedy (Greedy.java) and Blum-Yang-Lee-Tromp-Yannakakis (Assign.java) algorithms are available in the git repository at bitbucket.org/andkorsh/scss/src . There is also an executable class Main.java, which at startup asks for the number of starts to measure the speed of the algorithms and the path to the input file. Also, the Main class can generate input itself, for this instead of the file name you need to enter "random", after which the number of lines, the maximum line length, a fixed length or not and the number of characters in the alphabet will be requested. The report is written to the output.txt file.
Source codes are guaranteed to be compiled by javac starting from version “1.6.0_05”.
Testing is performed using the test function of the Main class.
[1] : Dan Gasfield. Lines, trees, and sequences in algorithms. Computer science and computational biology. Nevsky Dialect, BHV-Petersburg, 2003 - 656 p.: ISBN 5-7940-0103-8, 5-94157-321-9, 0-521-58519-8.
www.ozon.ru/context/detail/id/1393109
[2] : Dan Gusfield. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. THE PRESS SYNDICATE OF THE UNIVERSITY OF CAMBRIDGE, 1997 - 534 p.: ISBN-10: 0521585198, ISBN-13: 978-0521585194.
www.amazon.com/Algorithms-Strings-Trees-Sequences-Computational/dp/0521585198
[3] : Shunji Li, Wenzheng Chi. Lecture # 3: Shortest Common Superstring - CS 352 (Advanced Algorithms), Spring 2011.
cs.carleton.edu/faculty/dlibenno/old/cs352-spring11/L03-shortest-superstring.pdf
When I searched the Internet for information on this problem and its solution in Russian, there were only a couple of posts about bioinformatics, where these words are mentioned in passing. Of course, there was no code (except for the greedy algorithm). Having understood the problem, this fact has been advanced to an article here.
Caution, 4 megabytes!
For the most part, the article is an attempt to translate into an understandable language, illustrate, season with an example, and, of course, implement in Java a 4-approximate algorithm for constructing a superline from Dan Gasfield's book (see the literature used). But first, a small introduction and a 2-approximate, greedy algorithm.
In the simplest case (if the name of the problem did not contain the word “shortest”), the solution to the problem would be to simply concatenate the input strings in random order. But in this formulation of the problem, we are dealing with NP-completeness, which means that at present there is no algorithm with which to solve this problem on a Turing machine in a time not exceeding the polynomial in data size.
Input: S 1 , S 2 , ..., Sn is the set of lines of the finite alphabet E *.
Conclusion: X is a string of the alphabet E * containing each string S 1..n as a substring, where the length | X | minimized.
Example. Take the set of lines S = {abc, cde, eab}. In the case of concatenation, the length of the output superline will be 9 (X = abccdeeab), which is obviously not the best option, since lines can have a suffix-prefix match. The length of this match will be called overlap . (The choice of the English word was not accidental, since it does not have a specific and unambiguous translation into Russian. In Russian-language literature, the terms overlap, intersection, overlap and suffix-prefix match are usually used).
Retreat.The concept of overlap is one of the most important in the process of implementing algorithms for constructing add-ins. The calculation of overlap for an ordered pair of strings (S i , S j ) is reduced to finding the length of the maximum match of the suffix of the string S i with the prefix of the string S j .

One way to program to find overlap is presented in the following listing.
/*
* Функция вычисляет максимальную длину суффикса строки s1
* совпадающего с префиксом строки s2 (длину наложения s1 на s2)
*/
private static int overlap(String s1, String s2)
{
int s1last = s1.length() - 1;
int s2len = s2.length();
int overlap = 0;
for (int i = s1last, j = 1; i > 0 && j < s2len; i--, j++)
{
String suff = s1.substring(i);
String pref = s2.substring(0, j);
if (suff.equals(pref)) overlap = j;
}
return overlap;
}
Return for example. If we concatenate the strings S = {abc, cde, eab} taking into account their overlaps, we get the string X = abcdeab with a length of 7, which is shorter than the previous one, but not the shortest. The shortest string will be obtained when concatenating strings with overlaps in the order of 3-1-2, then the resulting string X = eabcde will have a length of 6. Thus, we reduced the problem to finding the optimal order of concatenating strings taking into account their overlaps.
Restriction. All existing algorithms for finding the shortest superstructures assume that no input set string is a substring of any other string. Deleting such lines can be done, for example, using the suffix tree and, obviously, does not detract from the generality.
Greedy algorithm
In this algorithm, at each iteration, we try to find the maximum overlap of any two lines and merge them into one. We hope that the result of this algorithm will be close to the actually optimal one.
1. While S contains more than one line, we find two lines with the maximum overlap and merge them into one (for example, ABCD + CDEFG = ABCDEFG).
2. We return one line remaining in S.
An example implementation of this algorithm is presented in the following listing.
/*
* Функция сливает строки с максимальным наложением до тех пор,
* пока не останется единственная строка (общая надстрока).
*/
public static String createSuperString(ArrayList strings)
{
while (strings.size() > 1)
{
int maxoverlap = 0;
String msi = strings.get(0), msj = strings.get(1);
for (String si : strings)
for (String sj : strings)
{
if (si.equals(sj)) continue;
int curoverlap = overlap(si, sj);
if (curoverlap > maxoverlap)
{
maxoverlap = curoverlap;
msi = si; msj = sj;
}
}
strings.add(merge(msi, msj, maxoverlap));
strings.remove(msi);
strings.remove(msj);
}
return strings.get(0);
}
Another simple merge function appeared in this listing, which merges two lines into one, taking into account their overlap. Since the latter has already been calculated, it is logical to simply pass it as a parameter.
/*
* Функция сливает строки s1 и s2 на длину len, вычисленную с
* помощью функции overlap(s1, s2)
*/
private static String merge(String s1, String s2, int len)
{
s2 = s2.substring(len);
return s1 + s2;
}
One example ( worst case ):
● Input : S = {“ab k ”, “b k c”, “b k + 1 ”}
● Output of the greedy algorithm: “ab k cb k + 1 ” with a length of 4 + 4k
● Conclusion of the optimal algorithm: “ab k + 1 c” with a length of 4 + 2k.
Approximation coefficient based on the worst case.

4-approximate Bloom-Yang-Lee-Tromp-Yannakakis algorithm
Generally speaking, this algorithm has no name and no one calls it like me. It is simply called a 4-approximate algorithm for constructing the shortest superline. But since Blum, Young, Lee, Tromp and Yannakakis came up with it, why not give such a headline?
For clarity , during the analysis of the algorithm I will give an example of constructing a superline for the set S = {S 0 : “cde”, S 1 : “abc”, S 2 : “eab”, S 3 : “fgh”, S 4 : “ ghf ”, S 5 :“ hed ”} .
Main ideathe algorithm is to find coverage by cycles of minimum full length for a complete directional weighted graph whose vertices are rows of a given set and the edge weight from S i to S j is equal to overlap (S i , S j ) for all i, j.
Graph for our example (the vertices for visibility are signed by i instead of S i ):

In my implementation, I will represent this graph as an adjacency matrix , which will be formed in the banal manner shown in the following listing (in section 16.17 [1] D. Gasfield argues that the matrix can be formed more efficiently, but the way this matrix is generated does not affect the consideration of this algorithm).
int n = strings.size();
// Вычисление матрицы overlap'ов для всех
// упорядоченных пар (Si, Sj).
int[][] overlaps = new int[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
overlaps[i][j] = overlap(strings.get(i), strings.get(j));
For our example, the adjacency matrix will look like this:

After the adjacency matrix is constructed, it becomes necessary to find a covering by cycles of minimum full length. Such coverage can be found by reducing this problem to the “assignment problem”. So, the task was to find the full purpose of the maximum weight (as it turned out, this step of the algorithm takes dominant time). Faster and easier ([1] p.16.19.13) this destination can be found by the greedy method.
Greedy appointment ([1] p.16.19.13)
Input data: matrix A of size k × k.
Result: full assignment M.
- Put M = Ø and declare all cells A accessible.
- while A has available cells do begin
- Among the available cells A, select the cell (i, j) of the highest weight.
- Place cell (i, j) in M and make cells in row i and column j inaccessible.
- end;
- Issue full assignment M.
It is possible to represent M in the code as an array (int [] M = new int [k]) and interpret the first part of instruction 2.2 as M [i] = j; since in the full assignment, each number from 0 to k occurs exactly once as the row index and exactly once as the column index.
An example of the full assignment calculation implementation is presented in the following listing.
/*
* Функция, вычисляющая полное назначение максимального
* веса жажным методом. Время - O(k*k*log(k))
*/
private static int[] assignment(int[][] a)
{
int n = a.length;
boolean[][] notallow = new boolean[n][n];
int[] m = new int[n];
while (true)
{
int max = -1, maxi = -1, maxj = -1;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (notallow[i][j]) continue;
if (a[i][j] > max)
{
max = a[i][j];
maxi = i; maxj = j;
}
}
}
if (max == -1) break;
m[maxi] = maxj;
for (int i = 0; i < n; i++)
{
notallow[maxi][i] = true;
notallow[i][maxj] = true;
}
}
return m;
}
Step-by-step calculation of the full assignment of the maximum weight by the greedy method for our example:

Now that the full assignment of the maximum weight has been calculated, it is necessary to calculate the coverage in cycles of the minimum total length. To do this, you need:
taking any (logical - zero) index of the full assignment as the beginning, put it in the loop, mark it used and see if its value is equal to the index of the beginning of the cycle? If so, end the cycle, put it in the cover of the cycles and start a new cycle, taking the first unlabeled element as the beginning. If not, take this value as an index and repeat the procedure until all elements are marked.
The representation of coverage by loops in memory can be organized as a list of row index lists.
Algorithm listing (assign - full assignment):
// Нахождение покрытия циклами минимальной полной длины
// для полного назначения assign
ArrayList> cycles
= new ArrayList>();
ArrayList cycle = new ArrayList();
boolean[] mark = new boolean[assign.length];
for (int i = 0; i < assign.length; i++)
{
if (mark[i]) continue;
cycle.add(i);
mark[i] = true;
if (assign[i] == cycle.get(0))
{
cycles.add(cycle);
cycle = new ArrayList();
i = 0;
}
else
{
i = assign[i] - 1;
}
}
For our example, finding coverage by loops will look like this:

The resulting coverage in cycles can be displayed on the original graph, leaving only those edges that fell into the coverage.

Assembly. Now that all the cycles in the coverage have been calculated, you can start assembling, directly, the superstructure.
To do this, you need the prefix function, which takes the strings S 1 and S 2 and returns the string S 1 cut off to the right by overlap (S 1 , S 2 ) characters. But since all overlaps were counted by us for a long time, the function can be written so that it takes only one line and the number of characters by which it needs to be shortened.
/*
* Функция возвращает строку s1, обрезанную справа
* на ov символов
*/
private static String prefix(String s1, int ov)
{
return s1.substring(0, s1.length() - ov);
}
Now, for each cycle C i = {S 1 , S 2 , ..., S k-1 , S k }, it is necessary to compose the sub-line X Ci = prefix (S 1 , overlap (S 1 , S 2 )) ++ prefix (S 2 , overlap (S 2 , S ...)) ++ prefix (S ..., overlap (S ..., S k-1 )) ++ S k .
The problem is that, since loops in a coverage are loops , it means we can twist them cyclically and it is not clear which line to start constructing an X Ci superstructure with . The answer is simple - you need to shift the cycle so thatminimize overlap of the last and first line.
Consider the first cycle of cyclic coating from the example.

If you do not minimize the overlap of the last and first lines, but take C 0 = {1, 0, 2}, then the line will be X C0 = abc ++ cde ++ eab = abcdeab, which is obviously not the shortest possible. The minimum overlap in this loop is 1, which means that any of the sequences {0, 2, 1} (cde ++ eab ++ abc = cdeabc) or {2, 1, 0} (eab ++ abc ++ cde = eabcde).
The following is a code that cyclically shifts each cycle in the coverage so as to minimize overlap of the first and last lines of each cycle, and constructs add-ins for each cycle.
// Циклический сдвиг каждого цикла в покрытии такой, чтобы
// минимизировать overlap первой и последней строки в цикле
// и конструирование надстроки для каждого цикла.
ArrayList superstrings = new ArrayList();
for (ArrayList c : cycles)
{
String str = "";
ArrayList ovs = new ArrayList();
for (int i = 0; i < c.size() - 1; i++)
ovs.add(overlaps[c.get(i)][c.get(i+1)]);
int min = overlaps[c.get(c.size()-1)][c.get(0)];
int shift = 0;
for (int i = 0; i < ovs.size(); i++)
if (ovs.get(i) < min)
{
min = ovs.get(i);
shift = i + 1;
}
Collections.rotate(c, -shift);
for (int i = 0; i < c.size() - 1; i++)
str += prefix(strings.get(c.get(i)),
overlaps[c.get(i)][c.get(i+1)]);
str += strings.get(c.get(c.size()-1));
superstrings.add(str);
}
We now have the shortest add-ins for each cycle in the coverage. The considered algorithm with a factor of 4 assumes a simple concatenation of these lines.
// Конкатенация всех надстрок из superstrings
StringBuilder superstring = new StringBuilder();
for (String str : superstrings)
superstring.append(str);
return superstring.toString();
Source codes and testing
The source codes for the greedy (Greedy.java) and Blum-Yang-Lee-Tromp-Yannakakis (Assign.java) algorithms are available in the git repository at bitbucket.org/andkorsh/scss/src . There is also an executable class Main.java, which at startup asks for the number of starts to measure the speed of the algorithms and the path to the input file. Also, the Main class can generate input itself, for this instead of the file name you need to enter "random", after which the number of lines, the maximum line length, a fixed length or not and the number of characters in the alphabet will be requested. The report is written to the output.txt file.
Source codes are guaranteed to be compiled by javac starting from version “1.6.0_05”.
Testing is performed using the test function of the Main class.
private static int test(ArrayList substrings, String superstring)
{
int errors = 0;
for (String substring : substrings)
if (superstring.indexOf(substring) < 0)
errors++;
return errors;
}
References
[1] : Dan Gasfield. Lines, trees, and sequences in algorithms. Computer science and computational biology. Nevsky Dialect, BHV-Petersburg, 2003 - 656 p.: ISBN 5-7940-0103-8, 5-94157-321-9, 0-521-58519-8.
www.ozon.ru/context/detail/id/1393109
[2] : Dan Gusfield. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. THE PRESS SYNDICATE OF THE UNIVERSITY OF CAMBRIDGE, 1997 - 534 p.: ISBN-10: 0521585198, ISBN-13: 978-0521585194.
www.amazon.com/Algorithms-Strings-Trees-Sequences-Computational/dp/0521585198
[3] : Shunji Li, Wenzheng Chi. Lecture # 3: Shortest Common Superstring - CS 352 (Advanced Algorithms), Spring 2011.
cs.carleton.edu/faculty/dlibenno/old/cs352-spring11/L03-shortest-superstring.pdf
