Counts for the smallest: BFS
In a previous post, we talked about going around the graph in depth. Today I would like to talk about a no less important graph theory algorithm - about breadth-first traversal.
Last time, we already learned to look for some way through the maze. I ask everyone to find the shortest path under cat.
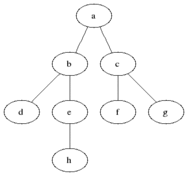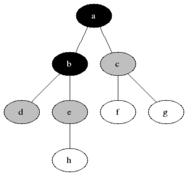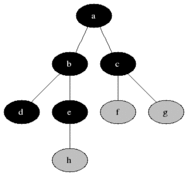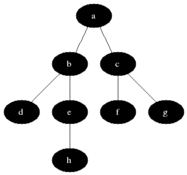 I intuitively want to consider the vertices of the graph in the order of increasing distance from the original one - as shown in the figure.
I intuitively want to consider the vertices of the graph in the order of increasing distance from the original one - as shown in the figure.
We divide all the vertices into three sets:
Obviously, as soon as all the vertices are black, the algorithm is completed. We will store all gray vertices in the queue and maintain the following property: the distances to all gray vertices in the order in which they lie in the queue do not decrease monotonously.
We get the first vertex from the queue (we denote it by v). For each of its neighbors w, one of two options is possible:
Repeat until there is at least one gray vertex.
> edges, and edges [v] contains the numbers of all vertices to which there is an edge from v. It is also assumed that the start variable stores the number of the initial vertex.
Evidence:
The maximum number of vertices simultaneously stored in the queue is V, that is, the maximum amount of memory used is O (V).
Next time I’ll try to consider a more complex problem on the basis of our favorite maze and, using its example, tell Dijkstra’s algorithm.
Last time, we already learned to look for some way through the maze. I ask everyone to find the shortest path under cat.
Formulation of the problem
It is required to find a path from one vertex of the graph to another, and the path should be minimal in the number of edges.Algorithm description
 I intuitively want to consider the vertices of the graph in the order of increasing distance from the original one - as shown in the figure.
I intuitively want to consider the vertices of the graph in the order of increasing distance from the original one - as shown in the figure. We divide all the vertices into three sets:
- Completely processed vertices (initially the set is empty, in the figure it is indicated in black)
- Vertices to which the distance is known (initially there is only one vertex in the set - the initial one, indicated in gray in the figure)
- Vertices about which nothing is known (initially - all vertices except the initial one are indicated in white in the figure)
Obviously, as soon as all the vertices are black, the algorithm is completed. We will store all gray vertices in the queue and maintain the following property: the distances to all gray vertices in the order in which they lie in the queue do not decrease monotonously.
We get the first vertex from the queue (we denote it by v). For each of its neighbors w, one of two options is possible:
- w is a black or gray top. In this case, we do not receive any new information.
- w is the white peak. Then the distance to it is d (w) = d (v) + 1. And, since we know the distance, w becomes a gray peak
Repeat until there is at least one gray vertex.
Implementation
It is assumed that the graph is stored in a vector arrayBfs
void BFS()
{
queue q;
// Инициализация: есть информация про начальную вершину
q.push(start);
d[start] = 0;
mark[start] = 1;
// Главный цикл - пока есть серые вершины
while (!q.empty())
{
// Берем первую из них
int v = q.front();
q.pop();
// Пробегаемся по всем ее соседям
for (int i = 0; i < (int)edges[v].size(); ++i)
{
// Если сосед белый
if (mark[edges[v][i]] == 0)
{
// То вычисляем расстояние
d[edges[v][i]] = d[v] + 1;
// И он становится серым
mark[edges[v][i]] = 1;
q.push(edges[v][i]);
}
}
}
}
Why does it work?
Consider any vertex v reachable from the initial one. Let p [0] = start, p [1], ..., p [k] = v be the shortest path from the initial vertex to the vertex v. Then the value d [v] = k obtained as a result of the operation of the algorithm.Evidence:
- d [v] ≤ k
- Base: the vertex p [0] = start is visited by the algorithm, and d [p [0]] = 0
- Assumption: the vertex p [i - 1] is visited by the algorithm, and d [p [i]] ≤ i
- Step: when considering the vertex p [i - 1] (or maybe earlier), we will consider the edge leading to the vertex p [i]. Thus, d [p [i]] ≤ i
- d [v] ≥ k
Suppose that d [v] <k. Consider the vertex v; the vertex, when considered, the vertex v was painted gray (we denote it by w); the vertex, when examined, the vertex w was painted gray; ...; start vertex start. Every two adjacent vertices in this sequence are connected by an edge according to the construction of the algorithm. Thus, we found a path from vertex start to vertex v of length shorter than k - a contradiction, therefore, d [v] ≥ k
Algorithm complexity
For each edge and each vertex, the algorithm performs a constant number of actions, therefore, the time complexity is O (V + E).The maximum number of vertices simultaneously stored in the queue is V, that is, the maximum amount of memory used is O (V).
Instead of a conclusion
In this article, we found the shortest path through a maze using one of the most famous graph theory algorithms - BFS.Next time I’ll try to consider a more complex problem on the basis of our favorite maze and, using its example, tell Dijkstra’s algorithm.
