October 29, 2013 at 16:09Data Transmission Efficiency and Information Theory
Encoding information in its simplest form arose during the communication of people in the form of gesture codes, and later in the form of speech, the essence of which is code words for conveying our thoughts to our interlocutor, then a new stage in the development of such coding began - writing, which allowed us to store and transmit information with the least loss from writer to reader. Hieroglyphs - there is a finite alphabet denoting concepts, objects or actions, the elements of which in some form are pre-agreed by people for the unique "decoding" of recorded information. Phonetic writing uses the alphabet for internal coding of speech words and also serves to uniquely reproduce recorded information. Numbers allow you to use the code representation of the calculations. But these types of coding served rather for direct communication,
The most important leap in the history of the development of information transfer was the use of digital data transfer systems. The use of analog signals requires a large redundancy of information transmitted in the system, and also has such a significant drawback as noise accumulation. Various forms of coding for converting analog signals to digital, storing, transmitting, and converting them back to analog form began their rapid development in the second half of the 20th century, and by the beginning of the 21st century, analog systems had almost been supplanted.
The main problem that needs to be solved when building a communication system was first formulated by Claude Shannon in 1948:
Such an accurate and clear statement of the problem of communication has had a huge impact on the development of communications. A new scientific branch appeared, which became known as the theory of information. The main idea, justified by Shannon, is that reliable communications should be digital, i.e. the communication problem should be considered as the transmission of binary digits (bits). There was an opportunity to unambiguously compare the transmitted and received information.
Note that any physical signal transmission channel cannot be absolutely reliable. For example, noise that spoils the channel and introduces errors into the transmitted digital information. Shannon showed that under certain fairly general conditions, it is possible in principle to use an unreliable channel to transmit information with an arbitrarily high degree of reliability. Therefore, there is no need to try to clear the channel of noise, for example, increasing the power of the signals (this is expensive and often impossible). Instead, efficient coding and decoding schemes for digital signals should be developed.
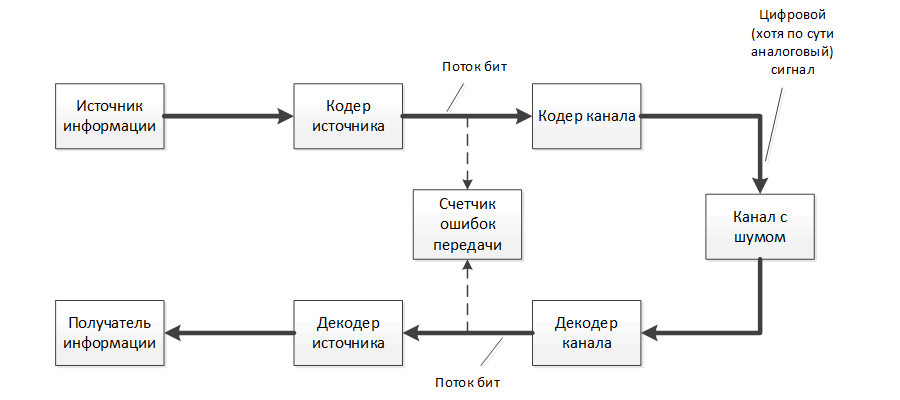
The task of channel coding (selection of the signal-code construction) is to build, on the basis of the known characteristics of the channel, an encoder that sends input symbols to the channel that will be decoded by the receiver with the maximum degree of reliability. This is achieved by adding some additional verification characters to the transmitted digital information. In practice, a telephone cable, satellite dish, optical disk, computer memory, or something else can serve as a channel. The task of source coding is to create a source encoder that produces a compact (shortened) description of the source signal, which must be transmitted to the addressee. The signal source can be a text file, a digital image, digitized music or a television broadcast. This concise description of the source signals may not be accurate. then we should talk about the discrepancy between the signal recovered after reception and decoding and its original. This usually happens when converting (quantizing) an analog signal into digital form.
Direct theorem:
Inverse theorem:
For additive white Gaussian noise, Shannon received the following expression:,
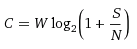where
C is the channel capacity, bits / s;
W is the channel bandwidth, Hz;
S is the signal power, W;
N is the noise power, W.
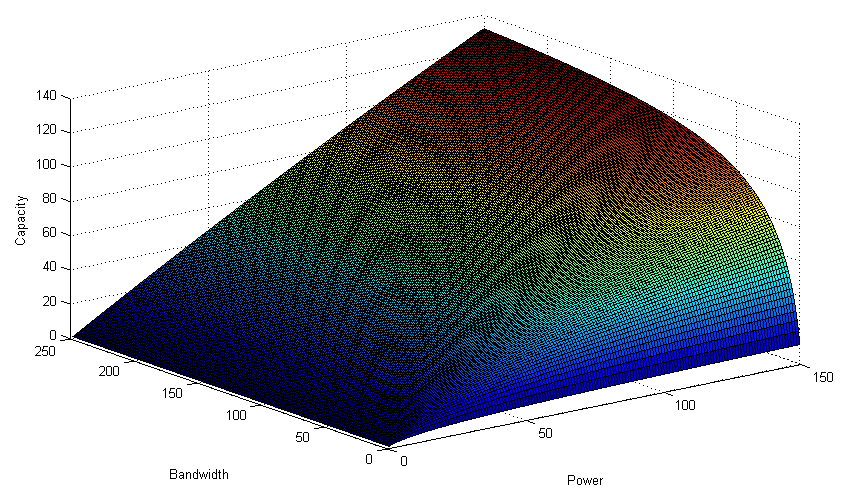
(Figure, for clarity, the relationship C (W, P) with N 0 = const; values from the ceiling, ask for them not to watch)
Since ABGS power grows linearly with the channel bandwidth, we have that the channel capacity has a limit C max = (S / N 0 ) log (2), with an infinitely wide frequency band (which grows linearly in power).
where
η is the spectrum utilization efficiency, bit / s / Hz;
T r- information transfer rate, bit / s;
W is the channel bandwidth, Hz.
Then,
using the energy value of the bit (for signals with complex signal-code structures, I understand the average energy value per bit) and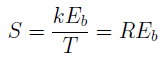 
, where
k is the number of bits per symbol transmitted to the channel;
T - character duration, s;
R is the transmission rate in the channel, bit / s;
E b - energy for the transmission of one bit in the channel;
N 0 - spectral density of noise power, W / Hz;
get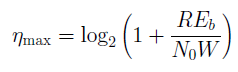
or 
.
The Shannon limit will be:
This limit makes sense for channels without codecs (R = T R), to achieve such efficiency, the received word must be of infinite length. For channels using error-correcting coding codecs, E b should be understood as the energy for transmitting one information bit rather than a channel bit (there may be different interpretations and I am ready to listen to alternative versions) => E b / N 0 in the channel is different from this value depending on the speed code (1/2, 3/4, 7/8 ...)
Thus, we see that there is a limit to the signal-to-noise ratio in the channel (E b / N 0) such that it is impossible to build a data transmission system in which you can achieve an arbitrarily low probability of error, with a higher noise level (there may be a system with just a low probability of error, with an extreme ratio!).
Gallager R. “Information Theory and Reliable Communication” - M.: “Soviet Radio”, 1974.
Salomon D. “Compressing Data, Images and Sound” - M .: “Technosphere”, 2004
Thank you for your attention, as a continuation, if interestingly, I can write an article with illustrations and a comparison of the effectiveness of signal-code constructions with respect to the Shannon border.
The most important leap in the history of the development of information transfer was the use of digital data transfer systems. The use of analog signals requires a large redundancy of information transmitted in the system, and also has such a significant drawback as noise accumulation. Various forms of coding for converting analog signals to digital, storing, transmitting, and converting them back to analog form began their rapid development in the second half of the 20th century, and by the beginning of the 21st century, analog systems had almost been supplanted.
The main problem that needs to be solved when building a communication system was first formulated by Claude Shannon in 1948:
The main property of a communication system is that it must accurately or approximately reproduce at a certain point in space and time a message selected at another point. Usually, this message makes some sense, but it is absolutely not important for solving the assigned engineering problem. The most important thing is that the message to be sent is selected from a family of possible messages.
Such an accurate and clear statement of the problem of communication has had a huge impact on the development of communications. A new scientific branch appeared, which became known as the theory of information. The main idea, justified by Shannon, is that reliable communications should be digital, i.e. the communication problem should be considered as the transmission of binary digits (bits). There was an opportunity to unambiguously compare the transmitted and received information.
Note that any physical signal transmission channel cannot be absolutely reliable. For example, noise that spoils the channel and introduces errors into the transmitted digital information. Shannon showed that under certain fairly general conditions, it is possible in principle to use an unreliable channel to transmit information with an arbitrarily high degree of reliability. Therefore, there is no need to try to clear the channel of noise, for example, increasing the power of the signals (this is expensive and often impossible). Instead, efficient coding and decoding schemes for digital signals should be developed.
The task of channel coding (selection of the signal-code construction) is to build, on the basis of the known characteristics of the channel, an encoder that sends input symbols to the channel that will be decoded by the receiver with the maximum degree of reliability. This is achieved by adding some additional verification characters to the transmitted digital information. In practice, a telephone cable, satellite dish, optical disk, computer memory, or something else can serve as a channel. The task of source coding is to create a source encoder that produces a compact (shortened) description of the source signal, which must be transmitted to the addressee. The signal source can be a text file, a digital image, digitized music or a television broadcast. This concise description of the source signals may not be accurate. then we should talk about the discrepancy between the signal recovered after reception and decoding and its original. This usually happens when converting (quantizing) an analog signal into digital form.
Direct theorem:
If the message rate is less than the bandwidth of the communication channel, then there are codes and decoding methods such that the average and maximum probabilities of decoding errors tend to zero when the block length tends to infinity.
In other words: For a channel with noises, you can always find such a coding system, for which messages will be transmitted with an arbitrarily high degree of fidelity, if only the source performance does not exceed the bandwidth of the channel.
Inverse theorem:
If the transmission speed is greater than the bandwidth, that is, then there are no such transmission methods in which the probability of error tends to zero with an increase in the length of the transmitted block.Wiki
For additive white Gaussian noise, Shannon received the following expression:,
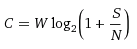where C is the channel capacity, bits / s;
W is the channel bandwidth, Hz;
S is the signal power, W;
N is the noise power, W.
(Figure, for clarity, the relationship C (W, P) with N 0 = const; values from the ceiling, ask for them not to watch)
Since ABGS power grows linearly with the channel bandwidth, we have that the channel capacity has a limit C max = (S / N 0 ) log (2), with an infinitely wide frequency band (which grows linearly in power).
where η is the spectrum utilization efficiency, bit / s / Hz;
T r- information transfer rate, bit / s;
W is the channel bandwidth, Hz.
Then,
using the energy value of the bit (for signals with complex signal-code structures, I understand the average energy value per bit) and 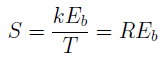, where k is the number of bits per symbol transmitted to the channel;
T - character duration, s;
R is the transmission rate in the channel, bit / s;
E b - energy for the transmission of one bit in the channel;
N 0 - spectral density of noise power, W / Hz;
get
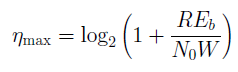or . The Shannon limit will be:
This limit makes sense for channels without codecs (R = T R), to achieve such efficiency, the received word must be of infinite length. For channels using error-correcting coding codecs, E b should be understood as the energy for transmitting one information bit rather than a channel bit (there may be different interpretations and I am ready to listen to alternative versions) => E b / N 0 in the channel is different from this value depending on the speed code (1/2, 3/4, 7/8 ...)
Thus, we see that there is a limit to the signal-to-noise ratio in the channel (E b / N 0) such that it is impossible to build a data transmission system in which you can achieve an arbitrarily low probability of error, with a higher noise level (there may be a system with just a low probability of error, with an extreme ratio!).
Literature
Gallager R. “Information Theory and Reliable Communication” - M.: “Soviet Radio”, 1974.
Salomon D. “Compressing Data, Images and Sound” - M .: “Technosphere”, 2004
Thank you for your attention, as a continuation, if interestingly, I can write an article with illustrations and a comparison of the effectiveness of signal-code constructions with respect to the Shannon border.