Optimization optimization in MatLab: nested and anonymous functions
Good afternoon!
I do research in control systems, and Matlab is my main work tool. One of the possibilities in MatLab is numerical optimization. You can optimize (minimize) any function that takes a vector of variable parameters as input and returns the value of the minimized criterion. Naturally, in the process of optimization, the objective function is called many times and its speed is essential. Matlab has good software tools that often can significantly improve performance, while maintaining the readability and ease of maintenance of the code. I will give an example of a task, show on it what anonymous functions and nested functions are, and then I will show how these two tools can be combined to significantly increase performance.
I thought for a long time about an example for optimization, I tried to choose something realistic - finding the optimal trajectory for a kinematically redundant manipulator, approximating experimental data, identifying parameters. But all this somehow led away from the essence, so I decided to dwell on an impractical, but illustrative example. So, the parameters a and b are given . It is necessary to find x in the range [0; 1] that maximizes the criterion:

where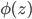 is some function that does not depend explicitly on x , but is needed to calculate the criterion. Let it be the module of the sum of the first million pseudorandom numbers obtained when setting seed to z . We write a matlab function that calculates the value of the criterion:
is some function that does not depend explicitly on x , but is needed to calculate the criterion. Let it be the module of the sum of the first million pseudorandom numbers obtained when setting seed to z . We write a matlab function that calculates the value of the criterion:
Please note that we return the value with a minus sign, since we want to find the maximum, and optimization is looking for the minimum.
Now, to optimize for specific values of a and b, we need to make an anonymous function. It is done like this:
Now the variable
The function
Let's see how this can be optimized. Obviously, every time
and here is the code:
Of course, this counts much faster. Optimization takes place, on average, in 0.8 ms. But the price for this is code degradation. Torn functional integrity - calculation
It’s good that matlab has a way around this situation. To do this, let's create a nested function inside the function
Nested function
And now the most interesting part is that the matlab can work with the anonymous nested function. Instead of a specific value, our function
Now, the
And such optimization is performed in 0.8 ms.
Result
We got the same speed as when explicitly carrying out the calculations in example c
In the future, if you intend to use the function both for optimization and just for calculations, then you can add one optional flag parameter to it. If it is not set, then the function returns a value. If specified, the handle to the nested function is returned.
I do research in control systems, and Matlab is my main work tool. One of the possibilities in MatLab is numerical optimization. You can optimize (minimize) any function that takes a vector of variable parameters as input and returns the value of the minimized criterion. Naturally, in the process of optimization, the objective function is called many times and its speed is essential. Matlab has good software tools that often can significantly improve performance, while maintaining the readability and ease of maintenance of the code. I will give an example of a task, show on it what anonymous functions and nested functions are, and then I will show how these two tools can be combined to significantly increase performance.
Statement of the problem and optimization
I thought for a long time about an example for optimization, I tried to choose something realistic - finding the optimal trajectory for a kinematically redundant manipulator, approximating experimental data, identifying parameters. But all this somehow led away from the essence, so I decided to dwell on an impractical, but illustrative example. So, the parameters a and b are given . It is necessary to find x in the range [0; 1] that maximizes the criterion:

where
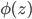 is some function that does not depend explicitly on x , but is needed to calculate the criterion. Let it be the module of the sum of the first million pseudorandom numbers obtained when setting seed to z . We write a matlab function that calculates the value of the criterion:
is some function that does not depend explicitly on x , but is needed to calculate the criterion. Let it be the module of the sum of the first million pseudorandom numbers obtained when setting seed to z . We write a matlab function that calculates the value of the criterion:function J = GetJ(a,b,x)
randn('seed',a);
phi_a=abs(sum(randn(1,1e6)));
randn('seed',b);
phi_b=abs(sum(randn(1,1e6)));
J=-(phi_a*x^2+phi_b*sqrt(1-x^2));
end
Please note that we return the value with a minus sign, since we want to find the maximum, and optimization is looking for the minimum.
Now, to optimize for specific values of a and b, we need to make an anonymous function. It is done like this:
a=121233;
b=31235;
fhnd_GetJ = @(x) GetJ(a,b,x);
Now the variable
fhnd_GetJcontains the handle of the anonymous function, which takes one parameter and allows you to calculate GetJ(a,b, принятый параметр)for the values of a and b specified when creating this anonymous function. You can go directly to minimization. Let's say we want to find the optimal value of x with an accuracy of 1 millionth:opt=optimset('TolX',1e-6);
optimal_x=fminbnd(fhnd_GetJ,0,1,opt);
The function
fminbnd(fun,x_min,x_max)minimizes the scalar function of the scalar argument on the interval [ x_min ; x_max ]. Here funis the handle of the function to be optimized. When performing the optimization, the function GetJis called 12 times, this can be seen by setting the options in the options ‘Display’as it ‘iter’will show all iterations. On my computer, optimization takes, on average, 10 ms.Performance boost
Let's see how this can be optimized. Obviously, every time
GetJwe call a function, we completely count in vain the values phi_aand phi_b, since they do not change with the variation of x and depend only on the given values of a and b . How can you save here? The most common option that I come across is to make preliminary calculations from the objective function. Make such a functionfunction J = GetJ2(phi_a,phi_b,x)
J=-(phi_a*x^2+phi_b*sqrt(1-x^2));
end
and here is the code:
randn('seed',a);
phi_a=abs(sum(randn(1,1e6)));
randn('seed',b);
phi_b=abs(sum(randn(1,1e6)));
fhnd_GetJ2 = @(x) GetJ2(phi_a,phi_b,x);
optimal_x=fminbnd(fhnd_GetJ2,0,1,opt);
Of course, this counts much faster. Optimization takes place, on average, in 0.8 ms. But the price for this is code degradation. Torn functional integrity - calculation
phi_aand phi_bindependent value and does not apart from the calculation J is not necessary. If somewhere else you need to consider J (a, b, x) again , not just for optimization, but just like that, then instead of just calling GetJfor yourself , you also have to drag the calculation phi_aand phi_bor do separately functions for optimization, separately for calculations . Well, just not very beautiful. It’s good that matlab has a way around this situation. To do this, let's create a nested function inside the function
GetJ:function J = GetJ3(a,b,x)
randn('seed',a);
phi_a=abs(sum(randn(1,1e6)));
randn('seed',b);
phi_b=abs(sum(randn(1,1e6)));
J=nf_GetJ(x);
function out_val = nf_GetJ(x)
out_val=-(phi_a*x^2+phi_b*sqrt(1-x^2));
end
end Nested function
nf_GetJsees all the variables in the scope of the parent function and, in principle, it is clear what and how it does. So far, we have not received any performance gain - all the same 10 ms for optimization. And now the most interesting part is that the matlab can work with the anonymous nested function. Instead of a specific value, our function
GetJcan return a handle to its own nested function. And when the function is called on this handle, the parent function will not be executed, but its scope with the calculated parameters will remain! We write:function fhnd_J = GetJ4(a,b,x)
randn('seed',a);
phi_a=abs(sum(randn(1,1e6)));
randn('seed',b);
phi_b=abs(sum(randn(1,1e6)));
fhnd_J=@(x) nf_GetJ(x);
function out_val = nf_GetJ(x)
out_val=-(phi_a*x^2+phi_b*sqrt(1-x^2));
end
end
Now, the
fhnd_Jhandle of the function is written to the returned variable , which allows you to calculate the J value for the used parameters a and b , without calculating the variables phi_aand phi_b, but using the values calculated when creating the handle. Further, our optimization looks like this:fhnd_GetJ4=GetJ4(a,b,x);
optimal_x=fminbnd(fhnd_GetJ4,0,1,opt);
And such optimization is performed in 0.8 ms.
Result
We got the same speed as when explicitly carrying out the calculations in example c
GetJ2, but retained the integrity of the function and the convenience of its use. In the future, if you intend to use the function both for optimization and just for calculations, then you can add one optional flag parameter to it. If it is not set, then the function returns a value. If specified, the handle to the nested function is returned.
