Animation of transition from a globe to a two-dimensional map

I want to share my cartographic experiment with Habr, namely the animation of the transition from the Orthographic projection (globe) to Equidistant (one of the projections of ordinary two-dimensional maps). Also, this method is suitable for any other projections. The result of the experiments was such an animation:



As before, we will use the d3.js library , as before, we will make several implementations: SVG and Canvas. Both options can be effectively used for interactive infographics. Let `s start?

Start

I once saw an advertisement on TV (like Gazprom), where the globe just spins and then unfolds into a map. Beautiful cartoon, I liked it, well, I decided to do something similar, only interactive and for the Internet. Challenge accepted .

From simple to complex

Since we have already worked with maps ( Interactive SVG map using d3.js ), and with a globe too ( Interactive globe - SVG versus Canvas ), we will begin right away by implementing the transition from one projection to another. The first thing that comes to mind is to give everything to the library, because transition animation has already been implemented there: transitions . So I did. The full code of the first example can be viewed on GitHub : Globe to Map , to feel at bl.ocks.org : Globe to Map . Yes, if on bl.ocks.org you click on the block number in the upper left corner, then you will go to the corresponding gist on GitHub, so in the future I will give only one link.

So, what is that: focused- indicator of focusing on the country, ortho- projection indicator, speed- speed of rotation, start- start of rotation, corr- variable to save the rotation phase.

The function endall(transition, callback)counts the number of elements to which the transition will be applied (animation), and when everything is finished, it performs the function ( callback) fed to it . In principle, it can be replaced with SetTimeout, but it is better to use it nevertheless endall(transition, callback).

//Starter for function AFTER All transitions
function endall(transition, callback) { 
  var n = 0; 
  transition 
  .each(function() { ++n; }) 
  .each("end", function() { if (!--n) callback.apply(this, arguments); }); 
}

Rotation is implemented using d3.timer and applies only to pathwith a class ortho.

  //Globe rotating via timer
  d3.timer(function() {
    var λ = speed * (Date.now() - start),
    φ = -5;
    projection.rotate([λ + corr, φ]);
    g.selectAll(".ortho").attr("d", path);
  });

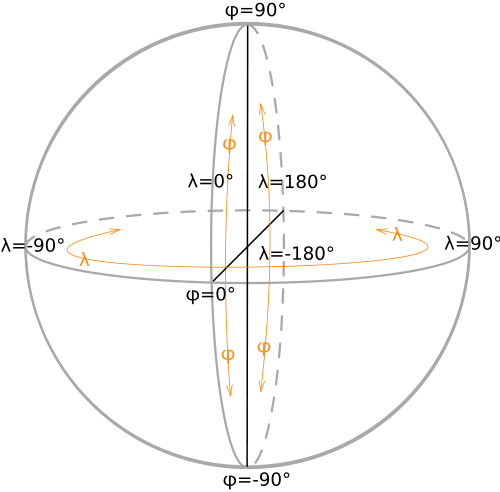
The variable corrallows us to return to the same angle of rotation of the globe that was before the change of projection. The following picture from the wiki article Geographic coordinates will help to understand longitude λand latitude :φ



Animation of the transition from the globe to the map:

//Transforming Globe to Map
if (ortho === true) {
  corr = projection.rotate()[0]; // <- save last rotation angle      
  g.selectAll(".ortho").classed("ortho", ortho = false);
  projection = projectionMap;
  path.projection(projection);
  g.selectAll("path").transition().duration(3000).attr("d", path);
}

Here we save the current rotation angle, then stop the rotation, remove the class ortho, change the projection and turn on the built-in transition animation.

The reverse transition is distinguished by the addition of a class orthofor all pathat the end of the transition and resetting the angle of rotation of the globe (the timer then ticked all this time).

//Transforming Map to Globe
projection = projectionGlobe;
path.projection(projection);
g.selectAll("path").transition()
.duration(3000).attr("d", path)
.call(endall, function() {
  g.selectAll("path").classed("ortho", ortho = true);
  start = Date.now(); // <- reset start for rotation
});

The rest of the code of questions, in theory, should not cause, especially if you read my previous articles.

If you played around with the first example for a while, you should have noticed that the map looks different every time. This is due to the fact that we initiate the transition at different angles of rotation of the globe ( λ), so the map is cut into different values ​​of longitude (meridians). To get the usual look of the map (section along the anti-meridian), we need to turn the globe to the zero meridian before the transition. Also, instead of a turnaround, you can change the projection parameters of a two-dimensional map, but I chose the first option. In the second example, antimeridian cutting is implemented, and the globe is rotated with the mouse (drag event). The function is responsible for the reversal defaultRotate():

//Rotate to default before animation
function defaultRotate() {
  d3.transition()
  .duration(1500)
  .tween("rotate", function() {
    var r = d3.interpolate(projection.rotate(), [0, 0]);
    return function(t) {
      projection.rotate(r(t));
      g.selectAll("path").attr("d", path);
    };
  })
};

I already described a similar function in the article Interactive globe - SVG versus Canvas , so I won’t repeat it. The code for the second example is bl.ocks.org : Globe to Map II .

It's time to complicate the animation, the metamorphoses of the first two examples look cool and have a right to exist, but I want something more aesthetic.

If beauty will save the world, then why does it constantly require some sacrifice? ©

In this case, victims mean complication of the code. So, so that the transition from one projection to another does not go “stupidly” along the shortest path, but beautifully, we need to create our own interpolation of the projections. I was lucky, I found a suitable example from Mike: Orthographic to Equirectangular . With minimal modifications, it can be used for transitions in both directions, just what we need. Here is its final implementation:

//Unreelling transformation
function animation(interProj) {
  defaultRotate();
  g.transition()
  .duration(7500)
  .tween("projection", function() {
    return function(_) {
      interProj.alpha(_);
      g.selectAll("path").attr("d", path);
    };
  })
}
function interpolatedProjection(a, b) {
  var projection = d3.geo.projection(raw).scale(1),
  center = projection.center,
  translate = projection.translate,
  clip = projection.clipAngle,
  α;
  function raw(λ, φ) {
    var pa = a([λ *= 180 / Math.PI, φ *= 180 / Math.PI]), pb = b([λ, φ]);
    return [(1 - α) * pa[0] + α * pb[0], (α - 1) * pa[1] - α * pb[1]];
  }
  projection.alpha = function(_) {
    if (!arguments.length) return α;
    α = +_;
    var ca = a.center(), cb = b.center(),
    ta = a.translate(), tb = b.translate();
    center([(1 - α) * ca[0] + α * cb[0], (1 - α) * ca[1] + α * cb[1]]);
    translate([(1 - α) * ta[0] + α * tb[0], (1 - α) * ta[1] + α * tb[1]]);
    if (ortho === true) {clip(180 - α * 90);}
    return projection;
  };
  delete projection.scale;
  delete projection.translate;
  delete projection.center;
  return projection.alpha(0);
}

At first glance it looks complicated, but in fact it is not. What is going on here? We feed the functions into interpolatedProjection(a, b)two projections, they are normalized (one scale, coordinates in radians), then a combined projection is created, which is the pairwise sum of the parameters (center, offset) of the original projections with a coefficient α(interpolation step). And at every step we are given a combined projection, depending on α. As the step increases α, the weight of the first projection decreases, and the weight of the second increases. Thus, we get a beautiful animation.
Final version at bl.ocks.org : Globe to Map III .

In the end, I also decided to make a version using canvas. This version is different in that all functions are moved insideready(error, world, countryData), since they must directly manipulate geodata, the rest of the logic is the same. There is nothing special to comment on, so here is the code on bl.ocks.org : Globe to Map IV .

results

We got an interesting blank for an interactive map, to which you can fasten any information, or you can loop and make the same cartoon. You can also make your visualization more sophisticated by adding shadows, gradients and other effects. Here are some examples of such whistles:

• Faux-3d shaded globe
• Floating landmasses
• See-through globe

You can still add satellite photos or even tiles on top of our schematic maps, making them more realistic, but this is a topic for a separate article, and it’s hardly appropriate for infographics.

This is where our experiment ends. Thanks to those who read to the end. Good luck to everyone and interesting projects.