About the stars
Sometimes I get the head of a problem that does not have any obvious practical value, but, nevertheless, they capture my imagination in one way or another, at least until I solve it. The practical value of the task, as a rule, is zero, but in the process others are solved that may have more value than the solved one.
It all started with a desire to study the properties of regular octagons and octagrams, but the results turned out to be applicable to all convex polygons (polygons) and stars built in them (by analogy I will call them polygrams - a pentagram, hexagram, septagram, octagram, etc. - although this the term has other meanings).
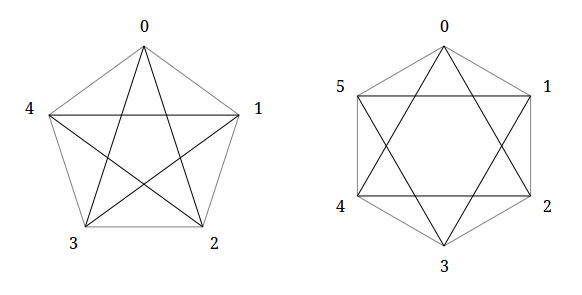
To start, terminology. The pentagram is the set of all diagonals of a pentagon; in the case of a hexagram, this is not all diagonals, but only those that connect the opposite vertices of the hexagon. In both cases, these peaks go through one from another. For example, if the vertices of a pentagon are renumbered(0, 1, 2, 3, 4) , then the pentagram is the set of lines (0, 2) , (1, 3) , (2, 4) , (3, 0) , (4, 1) . The hexagram (0, 1, 2, 3, 4, 5) , respectively, is a collection of lines (0, 2) , (1, 3) , (2, 4) , (3, 5) , (4, 0) , (5, 1) . Zeros as a starting point were taken not by chance and not as a tribute to programmatic thinking; I will describe the convenience of this notation below. The lines that make up the polygram, I will call the edges. The vertices of the polygram, I will call the vertices of the original polygon, and not all points of intersection of the edges.
The definition can be summarized by introducing the concept of “polygram order” as an integer k having a range of values between 1 and n / 2, where n is the number of angles of the original polygon. The upper boundary k (equal to the integer partn / 2 ) will determine the number of different generalized polygrams. The order itself means which vertex from the source should be connected by the diagonal included in the polygram. What does it mean? If we consider the numbers of vertices of the polygram, starting from zero, then they form an additive group of residues modulo n. Let m be the vertex number of the polygram. Then the segment connecting the vertex m and m + k (where k is the order of the polygram) in this group will be part of the polygram of order k. In this generalization, a polygram of order 1 coincides with the original polygon.
In the case of the pentagon, according to the formula, there are two generalized pentagrams - the pentagon itself and the pentagram in the classical sense.

In the case of a hex, there are three generalized hexagrams: the hex itself, the classic hexagram, and the diagonals connecting the opposite vertices (degenerate case).

For a better illustration, I will analyze the polygrams for the septagon and octagon. According to the formula, the number of septagrams will be three, the number of octagrams four.

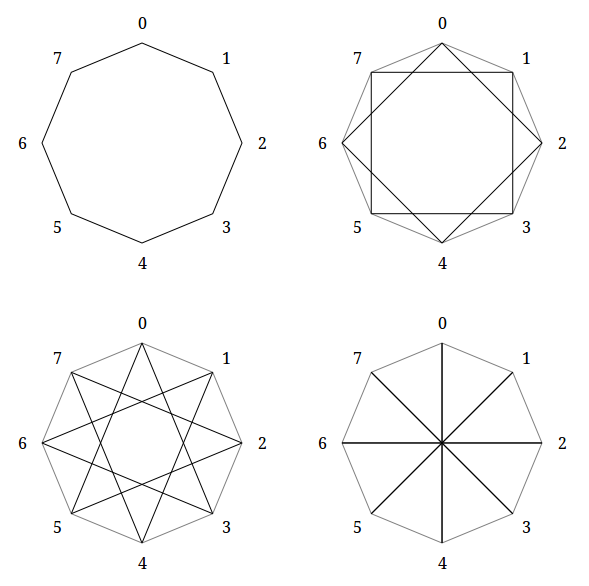
As a side effect, you can see that polygrams are naturally divided into connected and disconnected. Connected polygrams are polygrams between any pair of vertices of which there is a path along edges (you can jump from edge to edge only at the vertices of the polygon). Using the theory of numbers, you can notice that polygrams are connected if and only if the number of corners of the original polygon and the order of the polygram are mutually prime.
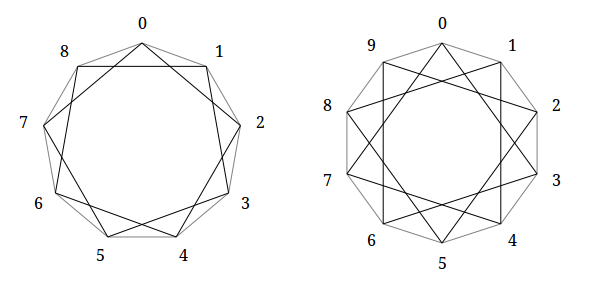
The picture below shows examples of disconnected polygrams, their individual parts are highlighted in different colors. A nonagram(n = 9, k = 3) splits into three triangles, a decagram (n = 10, k = 4) into two pentagrams:

Now the polygrams with the same number of angles (n = 9, k = 2 and n = 10, k = 3 ), but already connected:
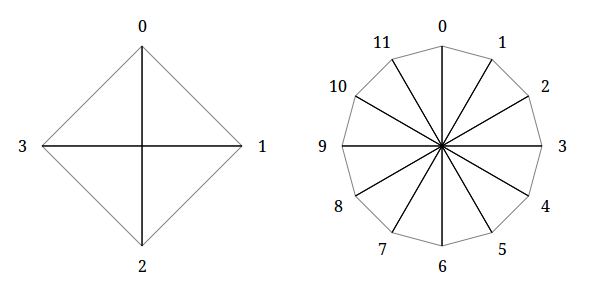
In addition, in the case of even n and maximum for such a case k (k = n / 2) polygons degenerate into a set of diagonals connecting opposite vertices.
Quite unexpected for me, the result was that the sum of the angles at the vertices of the polygrams (in the case of convex polygons) is a fairly simple computable quantity:π (n - 2k) . In the case of first-order polygrams (which coincide with the original polygon), the formula reduces to the well-known formula for calculating the angles of a polygon; in the case of a degenerate polygram, the sum of the angles turns out to be zero (which is natural). The proof of this fact is as follows: each edge of the polygram (for 1 <k <n / 2 - the case of a degenerate polygram is discarded and coincides with the original polygon) divides the polygon into two: one with k + 1 angle, the other with n - k + 1 . summing up the sum of the angles of all the smaller parts by the number of angles (whichk + 1 angle), we get the result π (k - 1) n (for each vertex of the polygon one (k + 1) -gon ). Each whole angle of the original polygon is present k - 1 times . In addition, once adjacent to the corners of the polygram, there are corners of the polygram. If we subtract from the first sum the sum of the integer corners of the polygram present in it (which is equal to π (n - 2) (k - 1) , since each whole angle occurs k - 1 times ), we get the sum of the angles π (k - 1) n - π (n - 2) (k - 1) adjacent to the corners of the polygram . If we subtract this sum of angles from the sum of the angles of the original polygon, we obtain the sum of the angles of the polygram:
π (n - 2) - (π (k - 1) n - π (n - 2) (k - 1)) = π (n - 2) - π (k - 1) n + π (n - 2) (k - 1) = π (n - 2) k - π (k - 1) n = π (n - 2k)
All The illustrations and arguments above apply to any polygrams built on convex polygons. In the figures, I depicted cases of correct polygrams solely from my own laziness - it was easier to write a drawing program. Further, we will focus only on the correct polygrams.
Based on the formula above, the angle at the vertex of a regular polygram isπ - 2πk / n .
If we take the horizon (the set of external points) of the correct polygram, then this figure will be a non-convex 2n-gon (n is the number of vertices of the polygram. The borders of the figures on the right illustrate this:

Thus, there are n additional “extra” angles, which I will call the internal corners of the polygram. These angles are non-convex, from the sum of the polygon angles for a regular polygram they are(π (2n - 2) - π (n - 2k)) / n = π (n + 2k - 2) / n = π + 2π (k - 1 ) / n . The angles opposite to them are equal, respectively, π - 2π (k - 1) / n . This angle I will call the angle between the rays.
These calculations can be useful for constructing patterns and funny ornaments, which will be illustrated below for patient readers.
Next is the rather useless part, which gave me aesthetic pleasure at one time, but the result of which can be only the reader’s lost time, which was the reason for adding “Funny Tasks” to the hub.
It all started with a desire to study the properties of regular octagons and octagrams, but the results turned out to be applicable to all convex polygons (polygons) and stars built in them (by analogy I will call them polygrams - a pentagram, hexagram, septagram, octagram, etc. - although this the term has other meanings).
To start, terminology. The pentagram is the set of all diagonals of a pentagon; in the case of a hexagram, this is not all diagonals, but only those that connect the opposite vertices of the hexagon. In both cases, these peaks go through one from another. For example, if the vertices of a pentagon are renumbered

The definition can be summarized by introducing the concept of “polygram order” as an integer k having a range of values between 1 and n / 2, where n is the number of angles of the original polygon. The upper boundary k (equal to the integer part
In the case of the pentagon, according to the formula, there are two generalized pentagrams - the pentagon itself and the pentagram in the classical sense.

In the case of a hex, there are three generalized hexagrams: the hex itself, the classic hexagram, and the diagonals connecting the opposite vertices (degenerate case).

For a better illustration, I will analyze the polygrams for the septagon and octagon. According to the formula, the number of septagrams will be three, the number of octagrams four.


As a side effect, you can see that polygrams are naturally divided into connected and disconnected. Connected polygrams are polygrams between any pair of vertices of which there is a path along edges (you can jump from edge to edge only at the vertices of the polygon). Using the theory of numbers, you can notice that polygrams are connected if and only if the number of corners of the original polygon and the order of the polygram are mutually prime.
The picture below shows examples of disconnected polygrams, their individual parts are highlighted in different colors. A nonagram

Now the polygrams with the same number of angles (

In addition, in the case of even n and maximum for such a case k (k = n / 2) polygons degenerate into a set of diagonals connecting opposite vertices.

Quite unexpected for me, the result was that the sum of the angles at the vertices of the polygrams (in the case of convex polygons) is a fairly simple computable quantity:
All The illustrations and arguments above apply to any polygrams built on convex polygons. In the figures, I depicted cases of correct polygrams solely from my own laziness - it was easier to write a drawing program. Further, we will focus only on the correct polygrams.
Based on the formula above, the angle at the vertex of a regular polygram is
If we take the horizon (the set of external points) of the correct polygram, then this figure will be a non-convex 2n-gon (n is the number of vertices of the polygram. The borders of the figures on the right illustrate this:

Thus, there are n additional “extra” angles, which I will call the internal corners of the polygram. These angles are non-convex, from the sum of the polygon angles for a regular polygram they are
These calculations can be useful for constructing patterns and funny ornaments, which will be illustrated below for patient readers.
Next is the rather useless part, which gave me aesthetic pleasure at one time, but the result of which can be only the reader’s lost time, which was the reason for adding “Funny Tasks” to the hub.
Octagram Pattern
For k = 2, the angle between the rays will be π - 2π / n , which is exactly equal to the angle of the original polygon in which the polygram is built. In what cases will such polygons be closely adjacent to each other, forming a kind of mosaic? in other words, the sum of the angle at the top of the polygram plus the doubled angle at the top of the polygon should be 2π. The angle at the vertex of the regular polygram in this case is π - 4π / n . Thus, we obtain the equation:
π - 4π / n + 2 (π - 2π / n) = 2π
3π - 8π / n = 2π
8π / n = pi;
n = 8
Thus, an octagram with k = 2 can be obtained by drawing 8 octagons, the neighboring of which have a common side - the inner sides of such polygons form the horizon of such an octagram.

The octagram(n = 8, k = 2) is disconnected and consists of two squares (the angles at all vertices are straight: π - 4 π / 8 = π / 2 ). On the rays of such an octagram, you can build squares with a side equal to the side of the beam.
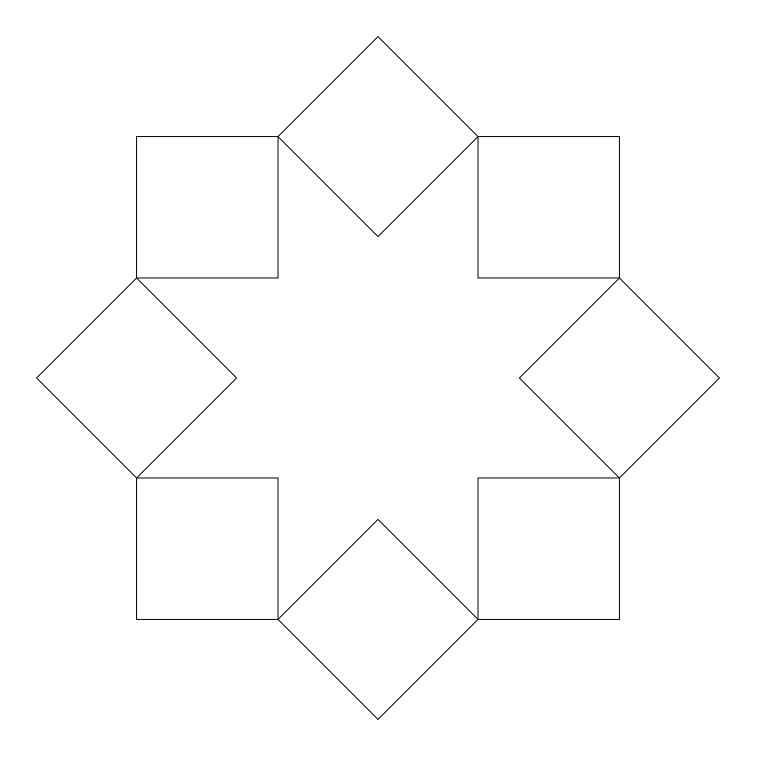
The inner corner of this octagram is5π / 4 . Subtracting from the internal angle the sum of the angles of the squares built on the rays, we get the angle between the sides of adjacent squares inside the octogram. This angle is π / 4 . So, the inner sides of the squares form a star-shaped figure with angles at eight vertices π / 4 and angles between the rays π / 2 (angle at the apex of the square). Thus, the internal angles of this figure will be 3π / 2 .
If we now consider the angles of the octagram(n = 8, k = 3) , we find that the angle at the vertex is π - 2πk / n = π / 4 , and the internal angles π + 2π (k - 1) / n = 3π / 2 , which exactly matches the figure bounded by the squares described above.
An illustration of these calculations is a nice picture:

Thus, an octagram with k = 2 can be obtained by drawing 8 octagons, the neighboring of which have a common side - the inner sides of such polygons form the horizon of such an octagram.

The octagram

The inner corner of this octagram is
If we now consider the angles of the octagram
An illustration of these calculations is a nice picture:

Hexagon-hexagram mosaic
Consider again the case k = 2 . As described above in the case of the octagram, in this case a regular polygon with the number of angles equal to the number of vertices of the polygram can be inscribed in the angle between the rays of the regular polygram. The sum of the angles of two polygons and beam polygrams to which they are adjacent, in the case of n> 8 exceeds 2p, in the case of n <8 is less than 2p. In the first case, building something interesting at the moment will not succeed, and in the second, you can enter something else in the remaining place. This can be another polygon or a ray of a polygram.
If this is the third polygon, then the number of sides can be calculated by the equation:
π - 4π / n + 3 (π - 2π / n) = 2π
2π - 10π / n = 0
n = 5
Thus, around the ray of a five-pointed star, you can draw three pentagons with a common vertex at the top of the pentagram. Unfortunately, in this case, a mosaic will not work, except for a pattern similar to that described above, where three pentagons are grouped around the top of each ray:

Considering the case with two polygons and two rays, we can come to the following equation:
2 (π - 4π / n) + 2 (π - 2π / n) = 2π
2π - 12π / n = 0
n = 6
The result is this mosaic:

If this is the third polygon, then the number of sides can be calculated by the equation:
Thus, around the ray of a five-pointed star, you can draw three pentagons with a common vertex at the top of the pentagram. Unfortunately, in this case, a mosaic will not work, except for a pattern similar to that described above, where three pentagons are grouped around the top of each ray:

Considering the case with two polygons and two rays, we can come to the following equation:
The result is this mosaic:

