Data compression by Huffman algorithm
Introduction
In this article I will talk about the well-known Huffman algorithm, as well as its application in data compression.
As a result, we will write a simple archiver. This has already been an article on Habré , but without practical implementation. The theoretical material of the current post is taken from the school lessons of computer science and from the book by Robert Laforet "Data Structures and Algorithms in Java". So, everything is under the cat!
A little thought
In a plain text file, one character is encoded with 8 bits (ASCII encoding) or 16 (Unicode encoding). Next we will consider the ASCII encoding. For example, take the string s1 = "SUSIE SAYS IT IS EASY \ n". There are a total of 22 characters in the line, of course, including spaces and the newline character - '\ n'. A file containing this string will weigh 22 * 8 = 176 bits. Immediately the question arises: is it rational to use all 8 bits to encode 1 character? We after all use not all characters of coding ASCII. Even if they used it, it would be more rational to give the shortest possible code, S, the shortest possible code, and for the rarest letter, T (or U, or '\ n'), give the code more authentic. This is the Huffman algorithm: you need to find the best encoding option, in which the file will be the minimum weight. Quite normal,
Coding
Why don't the 'S' character be given a code, for example, 1 bit long: 0 or 1. Let it be 1. Then the second most common character - '' (space) - will give 0. Imagine you started to decode your message - the encoded string s1 - and you see that the code starts with 1. So, what to do: is it a character S, or is it some other character, for example A? Therefore, an important rule arises:
No code should be a prefix of another.
This rule is the key to the algorithm. Therefore, the creation of a code begins with a frequency table, in which the frequency (number of occurrences) of each symbol is indicated:


10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110I separated the code of each character with a space. Truly in a compressed file this will not happen!
The question arises:
Building a Huffman Tree
Here come binary binary search trees. Do not worry, here the search, insert and delete methods are not required. Here is the java tree structure:
publicclassNode{
privateint frequence;
privatechar letter;
private Node leftChild;
private Node rightChild;
...
}
classBinaryTree{
private Node root;
publicBinaryTree(){
root = new Node();
}
publicBinaryTree(Node root){
this.root = root;
}
...
}
This is not a complete code, the full code will be lower.
Here is the tree building algorithm itself:
- Create a Node object for each character in the message (line s1). In our case there will be 9 nodes (Node objects). Each node consists of two data fields: symbol and frequency
- Create a Tree object (BinaryTree) for each node Node. The node becomes the root of the tree.
- Paste these trees into the priority queue. The lower the frequency, the higher the priority. Thus, when retrieving, the douvo is always selected by the lowest frequency.
Next you need to do the following cyclically:
- Extract the two trees from the priority queue and make them the descendants of the new node (the newly created node without a letter). The frequency of the new node is equal to the sum of the frequencies of the two descendant trees.
- For this node create a tree with a root in this node. Insert this tree back into the priority queue. (Since the tree has a new frequency, then it will most likely come to a new place in the queue)
- Continue to perform steps 1 and 2 until one tree is left in the queue - a Huffman tree
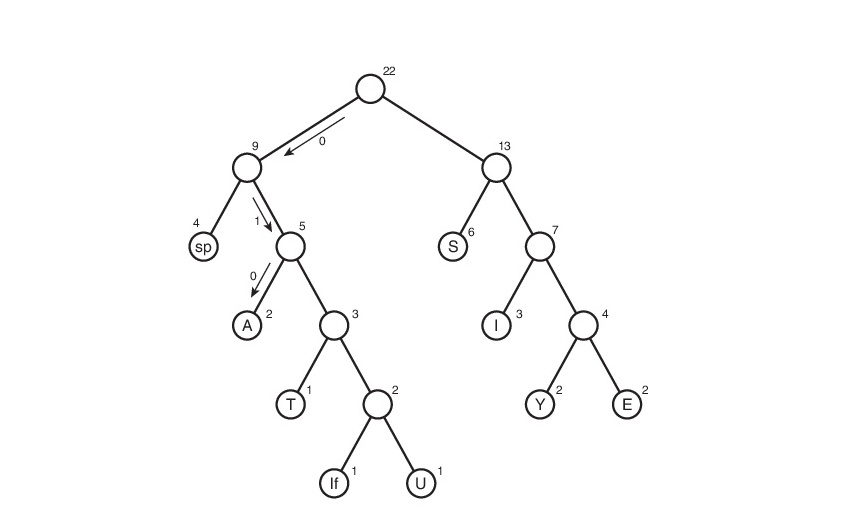
Consider this algorithm on line s1:

Here, the symbol “lf” (linefeed) denotes the transition to a new line, “sp” (space) is a space.
What's next?
We got a Huffman tree. OK. And what to do with it?
This is how the code table turned out. Note that if we consider this table, then we can conclude that the “weight” of each character is the length of its code. Then in the compressed form the source file will weigh: 2 * 3 + 2 * 4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 bits. At first he weighed 176 bits. Therefore, we have reduced it by 176/65 = 2.7 times! But this is utopia. Such a coefficient is unlikely to be obtained. Why? This will be discussed later.
Decoding
Well, perhaps the simplest thing is decoding. I think many of you have guessed that it is impossible to simply create a compressed file without any hints of how it was encoded - we will not be able to decode it! Yes, it was hard for me to realize this, but I would have to create a text file table.txt with a compression table:
01110
00
A010
E1111
I110
S10
T0110
U01111
Y1110
Write a table in the form of a "character" "character code." Why 01110 without a character? In fact, it’s with a symbol, just the java tools I’ve used when outputting to a file, the newline character is the '\ n' -convert to the newline transition (no matter how silly it sounds). Therefore, the blank line at the top is the symbol for code 01110. For code 00, the character is a space at the beginning of a line. I must say at once that
Having this table is very easy to decode. Recall what rule we followed when creating the encoding:
No code should be a prefix of another
This is where it plays a facilitating role. We read sequentially bit by bit and, as soon as the received string d, consisting of the read bits, coincides with the encoding corresponding to the character character, we immediately know that the character character was coded (and only that!). Next, write the character to the decoding line (the line containing the decoded message), reset the string d, and read the encoded file further.
Implementation
It's time to
Start over. First, write the Node class:
publicclassNode{
privateint frequence;//частотаprivatechar letter;//букваprivate Node leftChild;//левый потомокprivate Node rightChild;//правый потомокpublicNode(char letter, int frequence){ //собственно, конструкторthis.letter = letter;
this.frequence = frequence;
}
publicNode(){}//перегрузка конструтора для безымянных узлов(см. выше в разделе о построении дерева Хаффмана)publicvoidaddChild(Node newNode){//добавить потомкаif (leftChild == null)//если левый пустой=> правый тоже=> добавляем в левый
leftChild = newNode;
else {
if (leftChild.getFrequence() <= newNode.getFrequence()) //в общем, левым потомком
rightChild = newNode;//станет тот, у кого меньше частотаelse {
rightChild = leftChild;
leftChild = newNode;
}
}
frequence += newNode.getFrequence();//итоговая частота
}
public Node getLeftChild(){
return leftChild;
}
public Node getRightChild(){
return rightChild;
}
publicintgetFrequence(){
return frequence;
}
publicchargetLetter(){
return letter;
}
publicbooleanisLeaf(){//проверка на листreturn leftChild == null && rightChild == null;
}
}
Now the tree:
classBinaryTree{
private Node root;
publicBinaryTree(){
root = new Node();
}
publicBinaryTree(Node root){
this.root = root;
}
publicintgetFrequence(){
return root.getFrequence();
}
public Node getRoot(){
return root;
}
}
Priority queue:
import java.util.ArrayList;//да-да, очередь будет на базе спискаclassPriorityQueue{
private ArrayList<BinaryTree> data;//список очередиprivateint nElems;//кол-во элементов в очередиpublicPriorityQueue(){
data = new ArrayList<BinaryTree>();
nElems = 0;
}
publicvoidinsert(BinaryTree newTree){//вставкаif (nElems == 0)
data.add(newTree);
else {
for (int i = 0; i < nElems; i++) {
if (data.get(i).getFrequence() > newTree.getFrequence()) {//если частота вставляемого дерева меньше
data.add(i, newTree);//чем част. текущего, то cдвигаем все деревья на позициях справа на 1 ячейку break;//затем ставим новое дерево на позицию текущего
}
if (i == nElems - 1)
data.add(newTree);
}
}
nElems++;//увеличиваем кол-во элементов на 1
}
public BinaryTree remove(){//удаление из очереди
BinaryTree tmp = data.get(0);//копируем удаляемый элемент
data.remove(0);//собственно, удаляем
nElems--;//уменьшаем кол-во элементов на 1return tmp;//возвращаем удаленный элемент(элемент с наименьшей частотой)
}
}
The class that creates the Huffman tree:
publicclassHuffmanTree{
privatefinalbyte ENCODING_TABLE_SIZE = 127;//длина кодировочной таблицыprivate String myString;//сообщениеprivate BinaryTree huffmanTree;//дерево Хаффманаprivateint[] freqArray;//частотная таблицаprivate String[] encodingArray;//кодировочная таблица//----------------constructor----------------------publicHuffmanTree(String newString){
myString = newString;
freqArray = newint[ENCODING_TABLE_SIZE];
fillFrequenceArray();
huffmanTree = getHuffmanTree();
encodingArray = new String[ENCODING_TABLE_SIZE];
fillEncodingArray(huffmanTree.getRoot(), "", "");
}
//--------------------frequence array------------------------privatevoidfillFrequenceArray(){
for (int i = 0; i < myString.length(); i++) {
freqArray[(int)myString.charAt(i)]++;
}
}
publicint[] getFrequenceArray() {
return freqArray;
}
//------------------------huffman tree creation------------------private BinaryTree getHuffmanTree(){
PriorityQueue pq = new PriorityQueue();
//алгоритм описан вышеfor (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {//если символ существует в строке
Node newNode = new Node((char) i, freqArray[i]);//то создать для него Node
BinaryTree newTree = new BinaryTree(newNode);//а для Node создать BinaryTree
pq.insert(newTree);//вставить в очередь
}
}
while (true) {
BinaryTree tree1 = pq.remove();//извлечь из очереди первое дерево.try {
BinaryTree tree2 = pq.remove();//извлечь из очереди второе дерево
Node newNode = new Node();//создать новый Node
newNode.addChild(tree1.getRoot());//сделать его потомками два извлеченных дерева
newNode.addChild(tree2.getRoot());
pq.insert(new BinaryTree(newNode);
} catch (IndexOutOfBoundsException e) {//осталось одно дерево в очередиreturn tree1;
}
}
}
public BinaryTree getTree(){
return huffmanTree;
}
//-------------------encoding array------------------voidfillEncodingArray(Node node, String codeBefore, String direction){//заполнить кодировочную таблицуif (node.isLeaf()) {
encodingArray[(int)node.getLetter()] = codeBefore + direction;
} else {
fillEncodingArray(node.getLeftChild(), codeBefore + direction, "0");
fillEncodingArray(node.getRightChild(), codeBefore + direction, "1");
}
}
String[] getEncodingArray() {
return encodingArray;
}
publicvoiddisplayEncodingArray(){//для отладки
fillEncodingArray(huffmanTree.getRoot(), "", "");
System.out.println("======================Encoding table====================");
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {
System.out.print((char)i + " ");
System.out.println(encodingArray[i]);
}
}
System.out.println("========================================================");
}
//-----------------------------------------------------String getOriginalString(){
return myString;
}
}
A class containing which encodes / decodes:
publicclassHuffmanOperator{
privatefinalbyte ENCODING_TABLE_SIZE = 127;//длина таблицыprivate HuffmanTree mainHuffmanTree;//дерево Хаффмана (используется только для сжатия)private String myString;//исходное сообщениеprivateint[] freqArray;//частотаная таблицаprivate String[] encodingArray;//кодировочная таблицаprivatedouble ratio;//коэффициент сжатия publicHuffmanOperator(HuffmanTree MainHuffmanTree){//for compressthis.mainHuffmanTree = MainHuffmanTree;
myString = mainHuffmanTree.getOriginalString();
encodingArray = mainHuffmanTree.getEncodingArray();
freqArray = mainHuffmanTree.getFrequenceArray();
}
publicHuffmanOperator(){}//for extract;//---------------------------------------compression-----------------------------------------------------------private String getCompressedString(){
String compressed = "";
String intermidiate = "";//промежуточная строка(без добавочных нулей)//System.out.println("=============================Compression=======================");//displayEncodingArray();for (int i = 0; i < myString.length(); i++) {
intermidiate += encodingArray[myString.charAt(i)];
}
//Мы не можем писать бит в файл. Поэтому нужно сделать длину сообщения кратной 8=>//нужно добавить нули в конец(можно 1, нет разницы)byte counter = 0;//количество добавленных в конец нулей (байта в полне хватит: 0<=counter<8<127)for (int length = intermidiate.length(), delta = 8 - length % 8;
counter < delta ; counter++) {//delta - количество добавленных нулей
intermidiate += "0";
}
//склеить кол-во добавочных нулей в бинарном предаствлении и промежуточную строку
compressed = String.format("%8s", Integer.toBinaryString(counter & 0xff)).replace(" ", "0") + intermidiate;
//идеализированный коэффициент
setCompressionRatio();
//System.out.println("===============================================================");return compressed;
}
privatevoidsetCompressionRatio(){//посчитать идеализированный коэффициент double sumA = 0, sumB = 0;//A-the original sumfor (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
if (freqArray[i] != 0) {
sumA += 8 * freqArray[i];
sumB += encodingArray[i].length() * freqArray[i];
}
}
ratio = sumA / sumB;
}
publicbyte[] getBytedMsg() {//final compression
StringBuilder compressedString = new StringBuilder(getCompressedString());
byte[] compressedBytes = newbyte[compressedString.length() / 8];
for (int i = 0; i < compressedBytes.length; i++) {
compressedBytes[i] = (byte) Integer.parseInt(compressedString.substring(i * 8, (i + 1) * 8), 2);
}
return compressedBytes;
}
//---------------------------------------end of compression----------------------------------------------------------------//------------------------------------------------------------extract-----------------------------------------------------public String extract(String compressed, String[] newEncodingArray){
String decompressed = "";
String current = "";
String delta = "";
encodingArray = newEncodingArray;
//displayEncodingArray();//получить кол-во вставленных нулейfor (int i = 0; i < 8; i++)
delta += compressed.charAt(i);
int ADDED_ZEROES = Integer.parseInt(delta, 2);
for (int i = 8, l = compressed.length() - ADDED_ZEROES; i < l; i++) {
//i = 8, т.к. первым байтом у нас идет кол-во вставленных нулей
current += compressed.charAt(i);
for (int j = 0; j < ENCODING_TABLE_SIZE; j++) {
if (current.equals(encodingArray[j])) {//если совпало
decompressed += (char)j;//то добавляем элемент
current = "";//и обнуляем текущую строку
}
}
}
return decompressed;
}
public String getEncodingTable(){
String enc = "";
for (int i = 0; i < encodingArray.length; i++) {
if (freqArray[i] != 0)
enc += (char)i + encodingArray[i] + '\n';
}
return enc;
}
publicdoublegetCompressionRatio(){
return ratio;
}
publicvoiddisplayEncodingArray(){//для отладки
System.out.println("======================Encoding table====================");
for (int i = 0; i < ENCODING_TABLE_SIZE; i++) {
//if (freqArray[i] != 0) {
System.out.print((char)i + " ");
System.out.println(encodingArray[i]);
//}
}
System.out.println("========================================================");
}
}
A class that facilitates writing to a file:
import java.io.File;
import java.io.PrintWriter;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.Closeable;
publicclassFileOutputHelperimplementsCloseable{
private File outputFile;
private FileOutputStream fileOutputStream;
publicFileOutputHelper(File file)throws FileNotFoundException {
outputFile = file;
fileOutputStream = new FileOutputStream(outputFile);
}
publicvoidwriteByte(byte msg)throws IOException {
fileOutputStream.write(msg);
}
publicvoidwriteBytes(byte[] msg)throws IOException {
fileOutputStream.write(msg);
}
publicvoidwriteString(String msg){
try (PrintWriter pw = new PrintWriter(outputFile)) {
pw.write(msg);
} catch (FileNotFoundException e) {
System.out.println("Неверный путь, или такого файла не существует!");
}
}
@Overridepublicvoidclose()throws IOException {
fileOutputStream.close();
}
publicvoidfinalize()throws IOException {
close();
}
}
A class that facilitates reading from a file:
import java.io.FileInputStream;
import java.io.EOFException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.Closeable;
import java.io.File;
import java.io.IOException;
publicclassFileInputHelperimplementsCloseable{
private FileInputStream fileInputStream;
private BufferedReader fileBufferedReader;
publicFileInputHelper(File file)throws IOException {
fileInputStream = new FileInputStream(file);
fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream));
}
publicbytereadByte()throws IOException {
int cur = fileInputStream.read();
if (cur == -1)//если закончился файлthrownew EOFException();
return (byte)cur;
}
public String readLine()throws IOException {
return fileBufferedReader.readLine();
}
@Overridepublicvoidclose()throws IOException{
fileInputStream.close();
}
}
Well, the main class:
import java.io.File;
import java.nio.charset.MalformedInputException;
import java.io.FileNotFoundException;
import java.io.IOException;
import java.nio.file.Files;
import java.nio.file.NoSuchFileException;
import java.nio.file.Paths;
import java.util.List;
import java.io.EOFException;
publicclassMain{
privatestaticfinalbyte ENCODING_TABLE_SIZE = 127;
publicstaticvoidmain(String[] args)throws IOException {
try {//указываем инструкцию с помощью аргументов командной строкиif (args[0].equals("--compress") || args[0].equals("-c"))
compress(args[1]);
elseif ((args[0].equals("--extract") || args[0].equals("-x"))
&& (args[2].equals("--table") || args[2].equals("-t"))) {
extract(args[1], args[3]);
}
elsethrownew IllegalArgumentException();
} catch (ArrayIndexOutOfBoundsException | IllegalArgumentException e) {
System.out.println("Неверный формат ввода аргументов ");
System.out.println("Читайте Readme.txt");
e.printStackTrace();
}
}
publicstaticvoidcompress(String stringPath)throws IOException {
List<String> stringList;
File inputFile = new File(stringPath);
String s = "";
File compressedFile, table;
try {
stringList = Files.readAllLines(Paths.get(inputFile.getAbsolutePath()));
} catch (NoSuchFileException e) {
System.out.println("Неверный путь, или такого файла не существует!");
return;
} catch (MalformedInputException e) {
System.out.println("Текущая кодировка файла не поддерживается");
return;
}
for (String item : stringList) {
s += item;
s += '\n';
}
HuffmanOperator operator = new HuffmanOperator(new HuffmanTree(s));
compressedFile = new File(inputFile.getAbsolutePath() + ".cpr");
compressedFile.createNewFile();
try (FileOutputHelper fo = new FileOutputHelper(compressedFile)) {
fo.writeBytes(operator.getBytedMsg());
}
//create file with encoding table:
table = new File(inputFile.getAbsolutePath() + ".table.txt");
table.createNewFile();
try (FileOutputHelper fo = new FileOutputHelper(table)) {
fo.writeString(operator.getEncodingTable());
}
System.out.println("Путь к сжатому файлу: " + compressedFile.getAbsolutePath());
System.out.println("Путь к кодировочной таблице " + table.getAbsolutePath());
System.out.println("Без таблицы файл будет невозможно извлечь!");
double idealRatio = Math.round(operator.getCompressionRatio() * 100) / (double) 100;//идеализированный коэффициентdouble realRatio = Math.round((double) inputFile.length()
/ ((double) compressedFile.length() + (double) table.length()) * 100) / (double)100;//настоящий коэффициент
System.out.println("Идеализированный коэффициент сжатия равен " + idealRatio);
System.out.println("Коэффициент сжатия с учетом кодировочной таблицы " + realRatio);
}
publicstaticvoidextract(String filePath, String tablePath)throws FileNotFoundException, IOException {
HuffmanOperator operator = new HuffmanOperator();
File compressedFile = new File(filePath),
tableFile = new File(tablePath),
extractedFile = new File(filePath + ".xtr");
String compressed = "";
String[] encodingArray = new String[ENCODING_TABLE_SIZE];
//read compressed file//!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!check here:try (FileInputHelper fi = new FileInputHelper(compressedFile)) {
byte b;
while (true) {
b = fi.readByte();//method returns EOFException
compressed += String.format("%8s", Integer.toBinaryString(b & 0xff)).replace(" ", "0");
}
} catch (EOFException e) {
}
//--------------------//read encoding table:try (FileInputHelper fi = new FileInputHelper(tableFile)) {
fi.readLine();//skip first empty string
encodingArray[(byte)'\n'] = fi.readLine();//read code for '\n'while (true) {
String s = fi.readLine();
if (s == null)
thrownew EOFException();
encodingArray[(byte)s.charAt(0)] = s.substring(1, s.length());
}
} catch (EOFException ignore) {}
extractedFile.createNewFile();
//extract:try (FileOutputHelper fo = new FileOutputHelper(extractedFile)) {
fo.writeString(operator.extract(compressed, encodingArray));
}
System.out.println("Путь к распакованному файлу " + extractedFile.getAbsolutePath());
}
}
File with instructions readme.txt you have to write yourself :-)
Conclusion
Perhaps this is all I wanted to say. If you have something to say about
PS
Yes, yes, I'm still here, because I have not forgotten about the coefficient. For the string s1, the coding table weighs 48 bytes - much larger than the source file, and we did not forget about the additional zeros (the number of added zeros is 7) => the compression ratio will be less than one: 176 / (65 + 48 * 8 + 7) = 0.38. If you also noticed this, then
