Get ready, you are waited by extremely pedantic article which can quite save you on interview or save some hours at catching a bug in production!

I am now actively working on the second season of the “Guide for the Impostor” and am writing about the RSA cipher for SSH, which is obviously the most downloaded piece of code in IT history.

I want to fully understand this story. Who invented this cipher, how it works, why it works and whether it will work in the future . Now I have unearthed one damn interesting story . I am not a crypto-maniac and I see others literally being sucked into this area. But it is also interesting to me, because there are small minks everywhere, and me as a magpieattract shiny things in deep minks . I am also very good at metaphors.

In any case: last week I learned something strange and I want to share: it turns out that the mod and the remainder of the division are not the same thing . It’s really funny that some of the readers jump out of their seats and shout at these words: “But this is exactly what I have always tried to tell you and everyone else!”

Call the guys from the “mod is not the rest” sect! This is for you.

What is mod?

I had to study it, just like the last time such a topic surfaced. This is one of those things that you know , but do not remember. When you use mod, then divide one number by another and take the remainder. So: 5 mod 2 will be 1, because 5/2 = 2 with the remainder 1.

The term mod means modulo operation , with module 2 in this case. Most of the programming languages used %to describe such an operation: 5 % 2 = 1.

This is where we find ourselves in a strange gray area.

Dial Math

I remember how I taught it at school, and then I forgot. There is a type of mathematics called “modular arithmetic” that deals with cyclic structures. The easiest way to present this is the dial with cycle 12. For the mathematician, the dial is mod 12. If you want to understand whether it is possible to evenly divide 253 hours into days, then you can apply the operation 253 mod 24, the result will be 13 , so the answer is "no"! We can answer “yes” only if the result is 0.

Another question you can ask is: “If I leave at 6 pm, how much time will be on arrival after 16 hours?”. It will be 6 + 16 mod 12, that is, 10.

Cryptographers lovemodbecause when used with really large numbers, you can create something known as "one-way functions." These are special functions that make it easy to calculate something in one direction, but not in the opposite direction.

If I tell you that 9 is the result of a squaring, you can easily determine that there were 3 inlets. You have the whole process from beginning to end. If I say that 9 is the result mod 29, then it will be more difficult to understand what is at the entrance.

Cryptographers like this idea because they can use division with remainder with giant primes to generate cryptographic keys. This is a completely different story: if you want to read about it, you can buy a book or, even better, support my efforts to write it .

However, we will not deviate from the topic.

Remnants and math dial

Now we come to the point: modulo and a simple residue are the same when the numbers are positive, but differ in the case of negative numbers.

Consider this task:

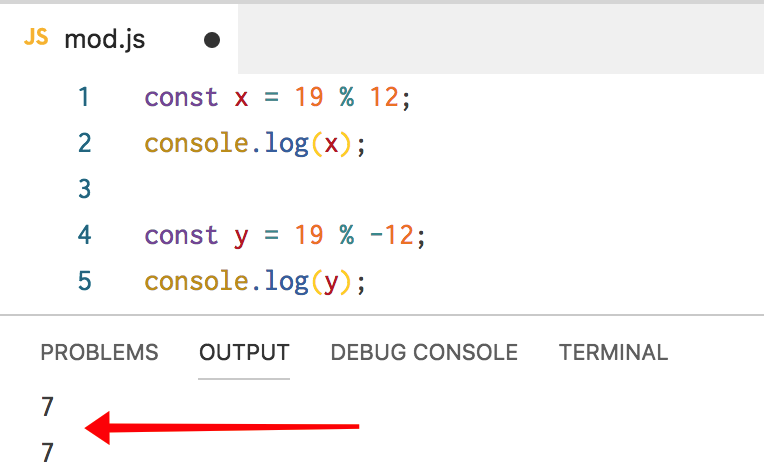
const x = 19% 12;
console.log(x);

What is the meaning x? We divide the numbers and get 7 as the remainder of 12. This is the right answer. How about this:

const y = 19% -12;
console.log(y);

Using regular math, we can multiply -12 by -1, which gives 12, and we still have 7, so our answer is again 7.

JavaScript agrees with this:



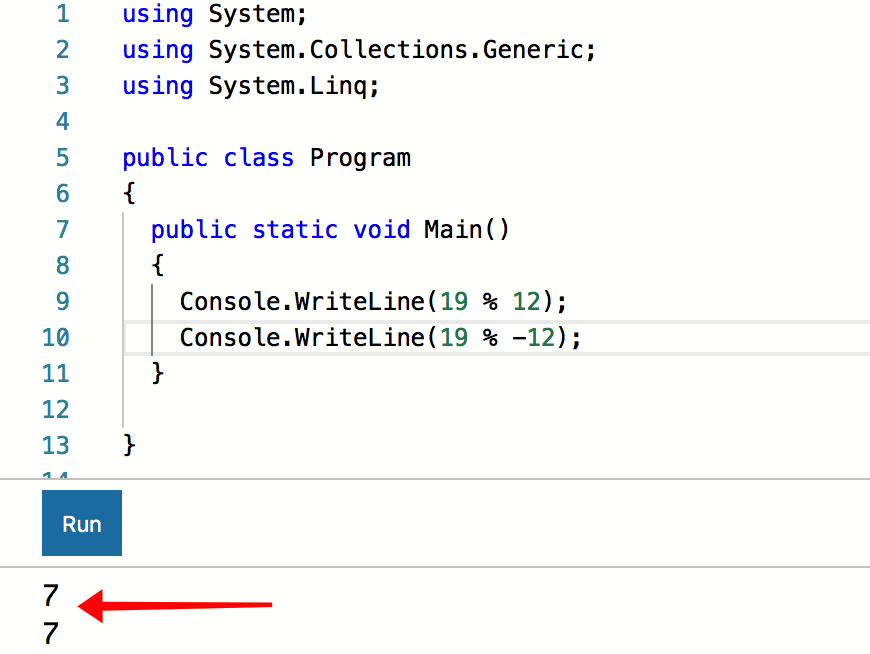
C # also agrees:



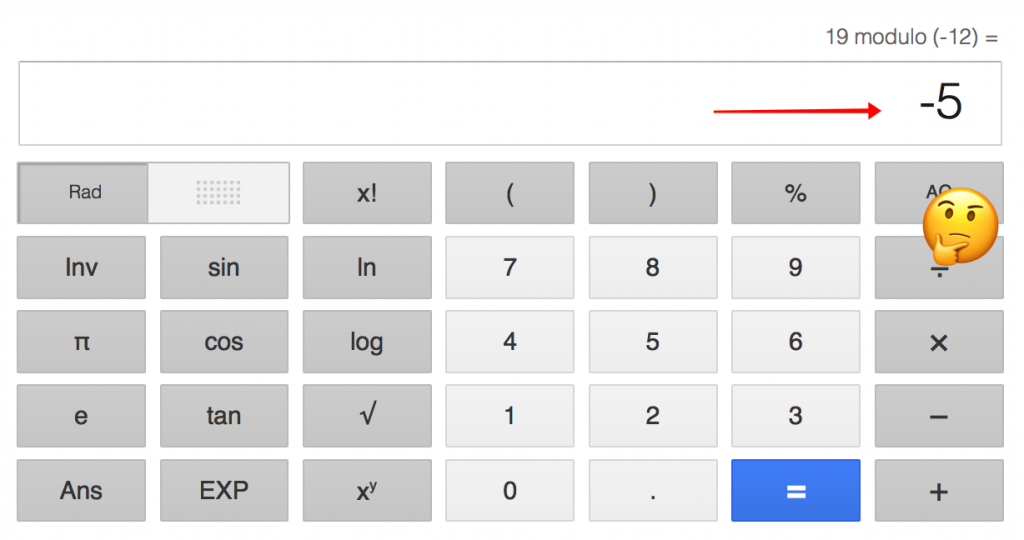
Google agrees with the first statement, but does not agree with the second:



Ruby agrees with Google:



In the name of Dijkstra, what is going on here?

Rotate the clock back

To answer the question, one should understand the difference between the remainder and modulo . Programmers combine these operations , but they should not do this, because they give the same result only if the divisor (12 in our case) is positive. You can easily send bugs to production if the divisor is negative.

But why is there a difference? Consider the positive divisor 19 mod 12on the clock: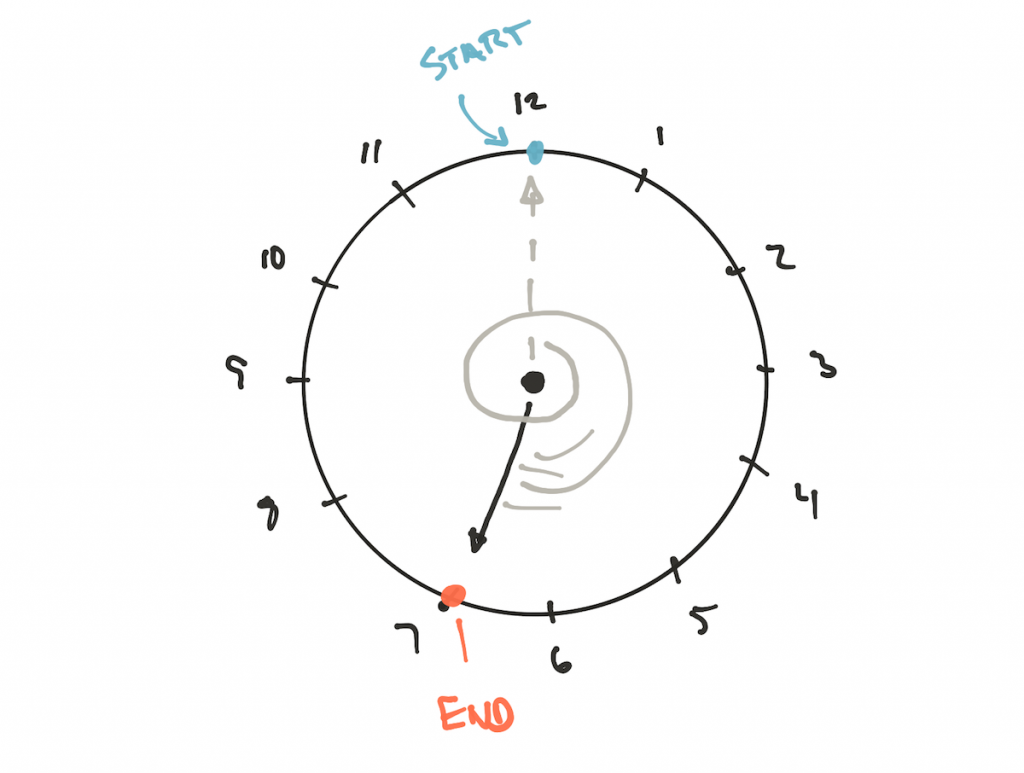



End result 7. We know this and we can prove it mathematically. But what about 19 mod -12? Here you need to use another watch :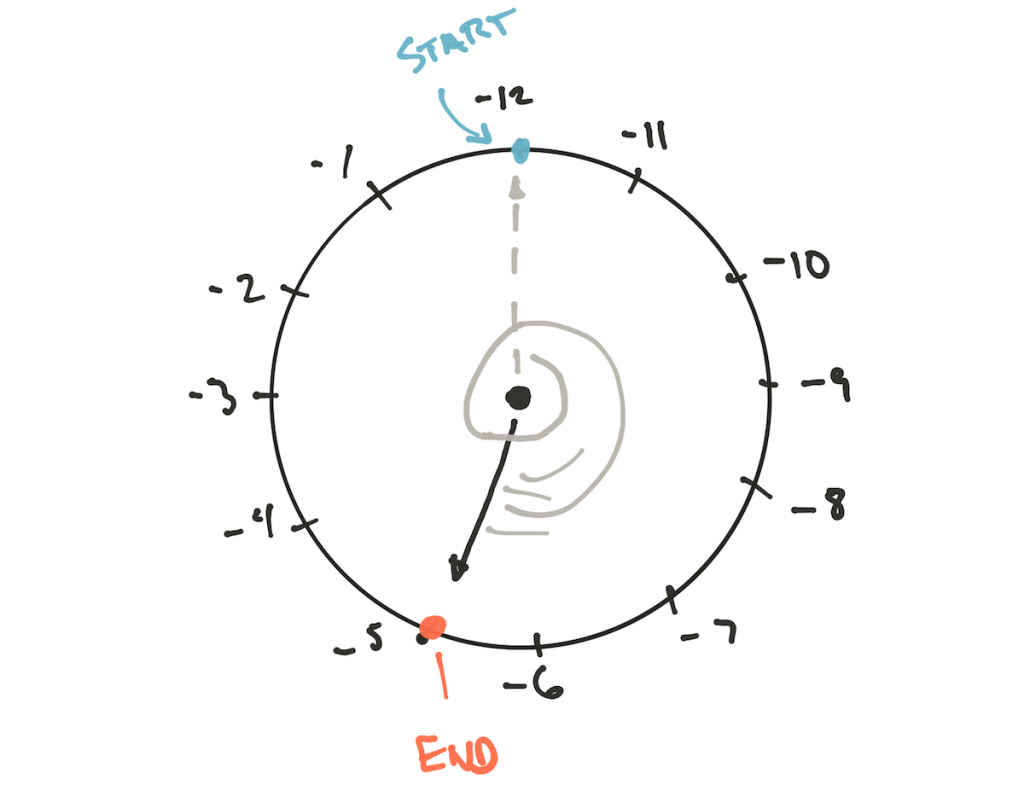



The modulus is -12, and we cannot ignore or change it by multiplying by -1, since modular arithmetic does not work that way. The only way to correctly calculate the result is to rearrange the marks on the clock so that we move from -12 or rotate the clock counterclockwise, which gives the same result.

Why not start marks with -1, moving to -2, etc.? Because in this case we will move backwards and constantly reduce the result until we reach -12, and at this moment we will make a jump of +12, and modulo does not work that way.

This is a famous thing.

Before calling me crazy and starting to google the topic: this is a known fact . In fact, the MDN (Mozilla Developer Network) even went so far as to call the %operation “remainder” (remainder), and not modulo:

The remainder operator returns the remainder of dividing one operand by another. He always takes the sign of the dividend .

Here is what Eric Lippert, one of the C # gods, says about modulo in C # :

However, this is not at all what the% operator actually does in C #. The% operator is not the canonical modulus operator, it is the remainder operator.

What is your language like?

So what?

I can understand if you have read this far, and now you are scratching your head and wondering if you should worry. I think it is worth it for two reasons:

1. I imagine how this question will take me by surprise at the interview.
2. I imagine how this one will get into production, and the developers will find out for a few hours why the math doesn't work.

This is also a fun fact in case your pedantic programmer friend appears next to you.