I make my quadrocopter. Part 1. The equations of dynamics

Table of contents

1. The equations of dynamics

Introduction

Once upon a time I wrote the following comment: That's it.
After such news, I sit down to make my quadrocopter. And then they all do it, but I don’t. No, but what.
Always wanted me to have some sort of flying thing. There were 2 radio-controlled helicopters. But it ended badly.
I decided to make my quadrocopter. How it will end - we'll see. I will not use any ready-made flight controllers, I will program everything myself. And I will try to describe this process in a series of articles. Now I present to your attention the first part. It will briefly show what equations of dynamics are hidden inside the quadrocopter.
So let's go.

1. Derivation of the equations of motion

The orientation of the quadrocopter in space is determined by three angles: yaw - ψ , pitch - θ , roll - φ .
Together they make up the vector
.
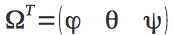The position of the device in the inertial reference system is set by the radius vector
.
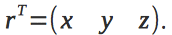The matrix of the transition from the coordinate system of the quadrocopter to the inertial coordinate system has the following form.

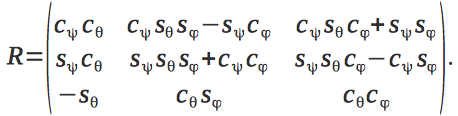
The traction force produced by each of the four engines is equal.

Here ω _i is the angular velocity of the engine, and b is the proportionality coefficient.
Now we can write a differential equation that describes the acceleration of the quadrocopter along the vertical axis.

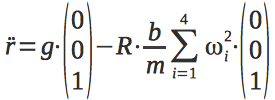
We immediately write the second differential equation.

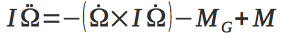
Here I is the inertia matrix, M is the torque applied to the quadrocopter, M _G is the gyroscopic moment.
Vector M is defined as follows:

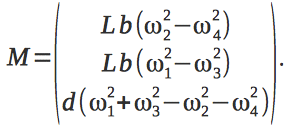
Here d is the drag coefficient, L is the shoulder length.
The gyroscopic moments caused by the rotation of the object with the rotating rotors of the engines are written as follows:


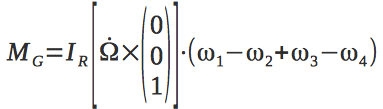
We introduce 4 control signals that will control the quadrocopter: The





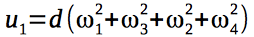
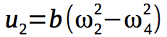
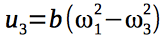
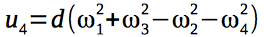
gyroscopic moments acting on the quadrocopter depend on the angular velocities of the rotors of the engines and, therefore, on the control vector


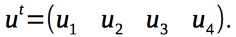
We write the system of equations describing our system.


And now we are transforming the system so that there are no second derivatives.


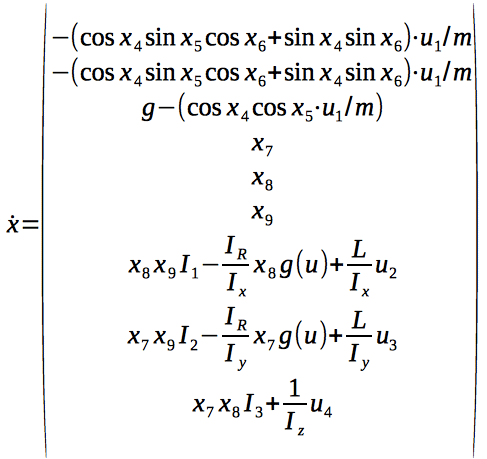
This system of 9 equations describes the dynamics of the system.

Conclusion

The post turned out to be somewhat ugly.
Tell me, please, an online formula editor? And then these look very disgusting.

Questions suggestions are welcome!