Lessons in Electrical Circuits - Transmission Lines, Part 2

This article is a translation. Start here .
Source .

In the program:
1) The wires hang in the air, but the current / voltage source sees a short circuit.
2) At one end of the wire, the amplitude is 0 volts, and at the other end, 1 volt. How is this possible?
3) Matching a 75 Ohm signal source with a 300 Ohm load using a properly selected cable.

Standing waves and resonance

Whenever there is a mismatch between the resistance of the transmission line and the load, reflection occurs. If the incident signal has one frequency, then this signal will be superimposed on the reflected waves, and a standing wave will appear.

The figure shows how a triangular incident wave is mirrored from the open end of the line. For simplicity, the transmission line in this example is shown as a single bold line, and not as a pair of wires. The incident wave goes from left to right, and the reflected wave goes from right to left.


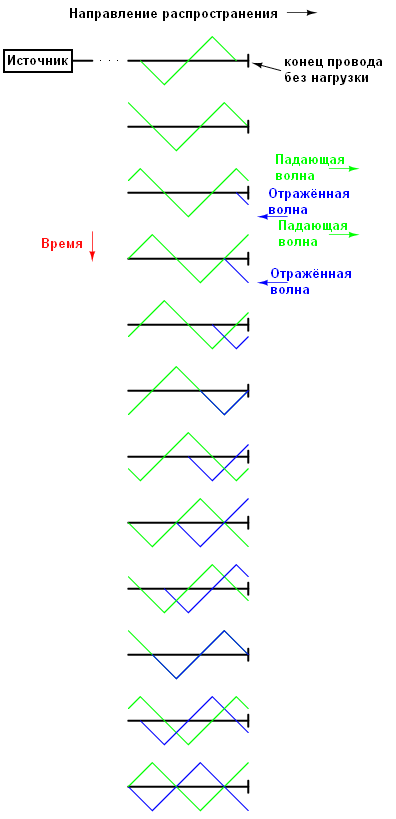
If we add these two signals, we will see that the third stationary signal is created along the entire length of the line: the red line in the figure below is the sum of the incident and reflected waves:

This third wave is the sum of the incident and reflected waves. It does not propagate through the cable, like an incident or reflected wave. Pay attention to the points along the line where the incident and reflected waves always cancel each other out: these points never change their position.

Standing waves are also common in the physical world. Consider a rope tied at one end and shake it:

The nodes (with points where there is no vibration) and antinodes (points of maximum vibration) remain unchanged along the entire length of the rope. String instruments also create a standing wave, with nodes of maximum and minimum vibration along their length. The main difference between a rope and a string instrument is that the instrument is already tuned to the correct vibration frequency:

Wind blowing through open pipes also produces standing waves. In this case, the air molecules in the tube oscillate, not the solid. A standing wave can end at a node (minimum amplitude) or antinode (maximum amplitude), and this depends on whether the other end of the tube is open or closed: The


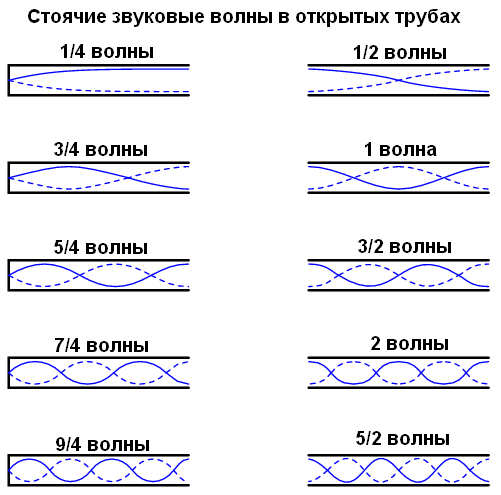
closed end of the pipe creates a node and the open end creates an antinode. By analogy, the string anchor is a knot, and the free end (if any) is the antinode.

Please note that standing waves of different frequencies may occur inside the pipe. There are several resonant frequencies for any system that supports standing waves.

Higher frequencies must be a multiple of the base frequency.

Actual frequencies for any of these harmonics (overtones) depend on the physical size of the pipe and the speed of wave propagation (in this case, the speed of sound propagation).

It is also possible to create standing waves in communication lines, and their frequency will depend on the type of load at the end of the line, on the propagation speed and physical length. Resonance in transmission lines is more complicated than resonance of strings or air in pipes, because we must take into account the voltage and current of the waves.

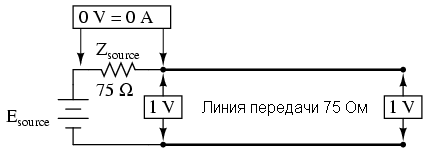
Resonance in transmission lines is easier to understand using computer simulation. To get started, consider a matched 75 ohm line:

Using SPICE to simulate the circuit, we indicate for the T1 line a wave impedance of 75 Ohms (z0 = 75) and a propagation delay of 1 μs. This is a convenient way to express the physical length of the transmission line — the amount of time it takes for the signal to propagate. For a real cable RG-59B / U it will be a length of 198 meters. 1 μs corresponds to a frequency of 1 MHz. I will select frequencies from zero to this frequency to show how the system responds to different frequencies.
Here is the SPICE model:

Transmission line v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 75 td = 1u rload 3 0 75 .ac lin 101 1m 1meg * Using "Nutmeg" program to plot analysis .end

We will perform this simulation and build a graph of the voltage drop at the source resistance (Zsource) - this will be a current indicator and a voltage graph at the end of the line (voltage at the load). We will see that the voltage source - the graph shows how vm (1) (the voltage between node 1 and ground point 0) is exactly 1 Volt. The voltages at point 2 and 3 will be 0.5 volts. The voltage across the resistor - as an indicator of current - will be 0.5 Volts:


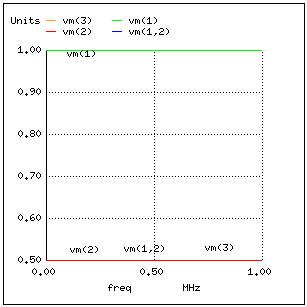
In a system where all resistances are perfectly matched, there can be no standing waves, and there are no resonances on the Bode plot .
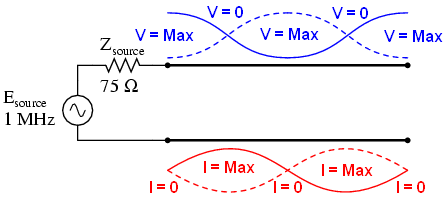
Now let's change the resistance to 999 megohms to simulate an open transmission line. We should definitely get reflected waves at some frequencies, from 1 MHz to 1 MHz:

Transmission line v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 75 td = 1u rload 3 0 999meg .ac lin 101 1m 1meg * Using "Nutmeg" program to plot analysis .end

Here, the line supply voltage vm (1) and the voltage at the load remain at the same level - 1V. Other voltage drops depend on the frequency (also from 1 MHz to 1 MHz). There are five noteworthy frequencies along the horizontal line: 0Hz, 250kHz, 500kHz, 750kHz, 1MHz. We study each point taking into account the voltage and current at various points in the circuit.

• 0Hz (actually 1MHz) is an almost constant current signal, and the circuit behaves as if 1V DC were applied. The current does not flow, since the zero voltage drop across the Zsource resistor is indicated, the graph is vm (1,2), and the voltage at the source is equal to the voltage at the end of the line vm (2) (voltage between point 2 and point 0).


• At 250 kHz, we see zero voltage at point 2, the maximum current from the source and the total voltage at the end of the line.


You may be wondering how this can be? How can we get the full voltage at the open end of the line if the input voltage is zero? The answer can be found in the standing wave paradox. At a frequency of 250 kHz, the line length is exactly equal to ¼ of the wavelength. Since the end of the line is open, there can be no current, but there will be voltage. Thus, at the end of the wire there will be a node for current (current is zero) and antinode for voltage (maximum amplitude):


• At a frequency of 500 kHz, exactly half the wave is laid in a line, and here we see another point at which the current is zero and the voltage again has a full amplitude:


• At a frequency of 750 kHz, the picture is similar to a frequency of 250 kHz: the voltage at the source is zero, and the maximum current. ¾ the wave fits into the line, as a result of which the source sees a short circuit at the point of connection to the transmission line even though there is a break at the other end of the line:


• When the frequency reaches 1 MHz, one full wave period fits in the line. At the moment, both current and voltage at the beginning of the line are equal to those at the end of the line. And if at the end of the line the current is zero (the resistance is 999 MΩ), then at the beginning of the line the current is also zero. The voltage at the source is equal to the voltage at the load. In fact, the source sees an open circuit.


Similarly, a short circuit at the end of the line generates standing waves, although the nodes and antinodes in current and voltage change places: At the short-circuited end of the line there will be no voltage (node), but there will be maximum current (antinode). Next is the SPICE simulation and illustrations of what happens at all interesting frequencies: 0Hz, 250 kHz, 500 kHz, 750 kHz, 1 MHz. A short circuit is modeled by a load resistance of 0 μOhm.

Transmission line v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 75 td = 1u rload 3 0 1u .ac lin 101 1m 1meg * Using "Nutmeg" program to plot analysis .end

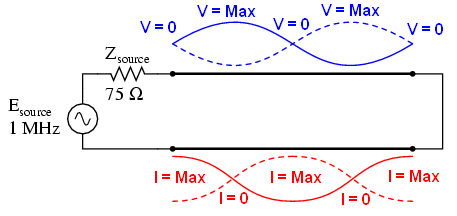
In both examples (open and short-circuited line) all energy is reflected. 100 percent of the incident wave reaches the end of the line and is reflected back to the source. If, however, the transmission line is loaded with some kind of resistance, there will be a difference between the maximum and minimum values ​​of voltage and current along the line.

Suppose we load a line with a 100 ohm resistor instead of 75:


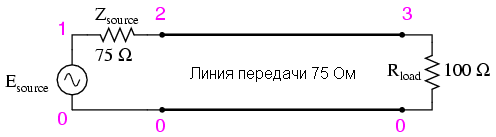
We build a model for this case:

Transmission line v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 75 td = 1u rload 3 0 100 .ac lin 101 1m 1meg * Using "Nutmeg" program to plot analysis .end

If we run another SPICE analysis with the output of text values ​​instead of a graph, we can find that all the interesting frequencies remain the same (DC, 250 kHz, 500 kHz, 750 kHz, and 1 MHz):

Transmission line v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0 = 75 td = 1u rload 3 0 100 .ac lin 5 1m 1meg .print ac v (1,2) v (1) v (2) v (3) .end

freq	v (1,2)	v (1)	v (2)	v (3)
1.000E-03	4.286E-01	1.000E + 00	5.714E-01	5.714E-01
2.500E + 05	5.714E-01	1.000E + 00	4.286E-01	5.714E-01
5.000E + 05	4.286E-01	1.000E + 00	5.714E-01	5.714E-01
7.500E + 05	5.714E-01	1.000E + 00	4.286E-01	5.714E-01
1.000E + 06	4.286E-01	1.000E + 00	5.714E-01	5.714E-01

At all frequencies, the voltage at the source at point 1 is 1 volt, as expected. The voltage at the load also remains constant, but has a lower amplitude (0.5714 Volts). However, the line voltage (point 2, graph v (2)) and current (graph v (1,2)) indicates that the current from the source varies with frequency.






At the odd harmonics of the fundamental frequency (250 kHz and 750 kHz), we see different voltage levels at the beginning and end of the line, because at these frequencies, standing waves create a node on one side of the line and antinode on the other. In contrast to the open and short-circuited lines, the maximum values ​​do not reach either zero or 100% of the original signal. But we still have points with a minimum and maximum voltage. The same is true for current. If the load resistance of the line does not correspond to the wave resistance of the line, we will have points of maximum and minimum current at some fixed points of the transmission line corresponding to nodes and antinodes.

One way to express the level of standing waves is the ratio of the maximum amplitude (at the antinode point) to the minimum amplitude for voltage or current. This ratio is called the SWR - standing wave coefficient. If the line is open or short-circuited, then the SWR is equal to infinity, since the minimum amplitude will be zero. In the example, a 75 Ohm line with a load of 100 Ohm SWR will be 1.333: the maximum line voltage at 250 or 750 kHz (0.5714 V) divided by the minimum line voltage (0.4286 V).

The SWR can also be calculated by knowing the load resistance and wave impedance of the line by dividing a larger value by a smaller one. In our example, 100Ω / 75Ω = 1.333.



A line with a perfectly matched load will have an SWR equal to 1. This is considered ideal not only because the reflected waves are energy that has not reached the load, but because of the high voltage and current: a high voltage can create a breakdown in the insulation, and high current damage the conductors.

Also, a line with poor SWR acts as an antenna. This is undesirable: such an antenna can interfere with nearby wires. Interestingly, antennas are open transmission lines, and they work with an SWR as close to 1. This means that all the energy is radiated.

The following photo shows the connection point in the communication line of the radio transmitter. Large copper pipes with a ceramic insulator are a rigid coaxial line with a wave impedance of 50 Ohms.



Flexible coaxial cable with a wave impedance of 50 ohms. A white plastic pipe connects the gas inside the pipes: they are sealed to protect against moisture. Pay attention to the flat wires for connecting the lines. Why aren't they round? This is due to the skin effect, which makes useless a large cross-sectional area at high frequencies.

Like many communication lines, they operate at low SWR. As we will see in the next section, the phenomenon of standing waves in communication lines is not always harmful, since they can be used for a useful function: impedance conversion.

Impedance conversion

Standing waves at the resonant points of short-circuited or open lines can produce unusual effects. With a line length of ½ wavelength (and a multiple of times greater), the source sees the load as it is. In the following illustrations, this is shown:




In both cases, at the ends of the line, the antinode for voltage and the node for current. The line imitates the load - infinite resistance, the source sees a break.
The same is true if there is a short circuit on the line: at the point of connection of the source there will be a minimum of voltage and a maximum of current.




However, if the line length is equal to a quarter of the wavelength, the source will see a break at a short circuit at the end of the line, and will see the broken line as a short circuit.

The line is open and the source sees a short circuit:




The line is closed and the source sees a break:



At these frequencies, the transmission line behaves like a resistance transformer, turning infinite resistance to zero and vice versa. This happens only at the resonant points, when a quarter of the wave fits in the line and is much larger (3/4, 5/4, 7/4, 9/4 ...), but if the frequency is known and unchanged, then this phenomenon can be used for matching different wave impedances with each other.
Take, for example, a 75Ω transmission line with a load of 100Ω. From the numerical simulation of SPICE we determine what resistance the source sees:






A simple equation relates the wave impedance of a line (Z0), the load impedance (Zload) and the input impedance (Zinput) for an inconsistent line at an odd harmonic:


Consider a practical example when you need to match a load of 300Ω and a source of 75Ω. All we need to do is calculate the correct line impedance and length for a quarter wavelength at 50 MHz.
First, calculate the line resistance. Z0 = Sqrt (75 * 300) = 150Ω.

Secondly, you need to calculate the length of the line. Suppose a shortening factor of 0.85, a speed of light of 300 thousand km / s, a signal speed of 255 thousand km / s. Divide this speed by the signal frequency and get a wavelength of 5.1 meters. We need a quarter wavelength - it will be 1,275m.

Here is a diagram for SPICE analysis:



We can indicate the line length by signal delay. At a frequency of 50 MHz, the period will be 20 ns. A quarter-wave delay time will be 5ns.

Transmission line v1 1 0 ac 1 sin rsource 1 2 75 t1 2 0 3 0 z0=150 td=5n rload 3 0 300 .ac lin 1 50meg 50meg .print ac v(1,2) v(1) v(2) v(3) .end

freq	v(1,2)	v(1)	v(2)	v(3)
5.000E+07	5.000E-01	1.000E+00	5.000E-01	1.000E+00

At a frequency of 50 MHz at point 1-2 exactly half - 0.5V drops, and the second half of the voltage drops on the communication line in the 2-0 circuit. This means that the source sees 75Ω in the load. The load, however, receives not half but 1 volt (voltage v (3)). At a resistance of 75Ω, 0.5V or 3.333mW drops - the same as at a load of 300 ohms at a voltage of 1V. In accordance with the maximum power theorem (Jacobi theorem), the maximum possible power is dissipated on the load. A quarter-wave transmission line with a wave impedance of 150Ω and a load of 300Ω behaves like a 75Ω load.

Of course, all this will work only at 50 MHz and odd harmonics. For other frequencies, the transmission line will have to be lengthened or shortened.

Oddly enough, a line of the same length will match a 300Ω source and a 75Ω load. This shows that the phenomenon of impedance conversion is fundamentally different from the principle of operation of a transformer with two windings.

Transmission line v1 1 0 ac 1 sin rsource 1 2 300 t1 2 0 3 0 z0 = 150 td = 5n rload 3 0 75 .ac lin 1 50meg 50meg .print ac v (1,2) v (1) v (2) v (3) .end

freq	v (1,2)	v (1)	v (2)	v (3)
5.000E + 07	5.000E-01	1.000E + 00	5.000E-01	2.500E-01

In this case, 0.5V, or 833μW, will fall on the internal resistance of the source. At the load there will be 0.25V - the same 833mW.

This method is often used to match transmission lines and antennas in radio transmitters, since there the frequency is often known and unchanged. The minimum impedance converter length corresponds to ¼ wavelength.