June 6, 2013 at 05:17Beale's hypothesis has risen to $ 1 million
The American Mathematical Society on Tuesday announced an increase in the reward to $ 1 million for proving Beale's hypothesis or for finding a counterexample.
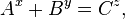
where
- natural and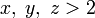 
, then 
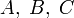they have a common simple divisor.
That is, if you pick up such numbers that A, B, C did not have a common prime divisor, then you will earn a million dollars.
The American banker, billionaire and math lover, Andrew Beal, put forward his hypothesis in 1993. Everyone can put forward a hypothesis, but the banker in 1997 managed to fuel the interest of the mathematical community by announcing an award for its proof or a counterexample. The reward was $ 5,000. Since then, Bill has raised rewards several times, and now it has grown to $ 1 million .
The trick is that proving Beale's conjecture means that Fermat’s Great Theoremcan be proven by contradiction. And over such elegant proof of Fermat’s Great Theorem, mathematicians have been struggling since 1637. The author himself said that it is. At the same time, the 1995 proof on 107 pages cannot be called elegant, and in the 17th century it could not be formulated in principle.
You can concentrate on finding a counterexample for Beale's hypothesis. To date, the values of all six variables up to 1000 have been checked . That is, in a successful counterexample, at least one variable must exceed 1000.
Hypothesis
If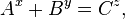where
- natural and 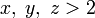, then 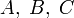they have a common simple divisor. That is, if you pick up such numbers that A, B, C did not have a common prime divisor, then you will earn a million dollars.
The American banker, billionaire and math lover, Andrew Beal, put forward his hypothesis in 1993. Everyone can put forward a hypothesis, but the banker in 1997 managed to fuel the interest of the mathematical community by announcing an award for its proof or a counterexample. The reward was $ 5,000. Since then, Bill has raised rewards several times, and now it has grown to $ 1 million .
The trick is that proving Beale's conjecture means that Fermat’s Great Theoremcan be proven by contradiction. And over such elegant proof of Fermat’s Great Theorem, mathematicians have been struggling since 1637. The author himself said that it is. At the same time, the 1995 proof on 107 pages cannot be called elegant, and in the 17th century it could not be formulated in principle.
You can concentrate on finding a counterexample for Beale's hypothesis. To date, the values of all six variables up to 1000 have been checked . That is, in a successful counterexample, at least one variable must exceed 1000.