Is it possible to instantly transfer information? Experiments with quantum entangled particles

Good day to all!
We continue to consider the possibilities of quantum mechanics for the transmission of information using the correlation of quantum-entangled particles. Unlike classical methods of communication, the use of quantum entangled particles provides the potential to instantly transfer information over long distances. The difficulty is to find ways to encode and decode the transmitted information. This article is devoted to finding solutions to this problem and the possibility of creating an experimental setup. If you are also interested in this task - welcome under the cut!

Let me remind you that in the last articlewe considered one of the possible schemes for transferring information between two remote objects. In particular, an optical scheme with beam splitters for receiving interference, as well as a detection and quantum erasure scheme using two down-converters was considered. In the comments there was a lot of discussion about the performance of such a scheme, as well as criticism from Hub users, that the use of down converters leads to interaction with the original particle, the phase shift of the interference pattern and other unpleasant consequences. I do not exclude such a possibility, so after detailed consideration I decided to exclude the use of down-converters and construct a circuit using circular and linear polarizers. Looking ahead, I can say that this solution has its own difficulties, due to which it is impossible to get a picture of interference. To solve these difficulties, we apply an elegant approach that follows from the consequence of quantum mechanics itself. I am deeply grateful to everyone who participated in the discussion of the previous article. Your arguments and criticism helped me to better understand the difficulties involved, to seek more information and find new solutions.

To begin, consider a real experimental setup . The laser beam hits a nonlinear optical device: a barium beta borate crystal (BBO), due to which one photon is converted into two entangled photons of lower frequency. The process is known as spontaneous parametric scattering. The resulting pair of photons follow different paths, one of which goes directly to detector 1 , and the second passes through a double slit and goes to detector 2 . Both detectors are connected to a coincidence circuit, ensuring that only entangled pairs of photons are counted. The stepper motor moves the second detector and scans the target area, creating an intensity map that forms a familiar interference pattern.


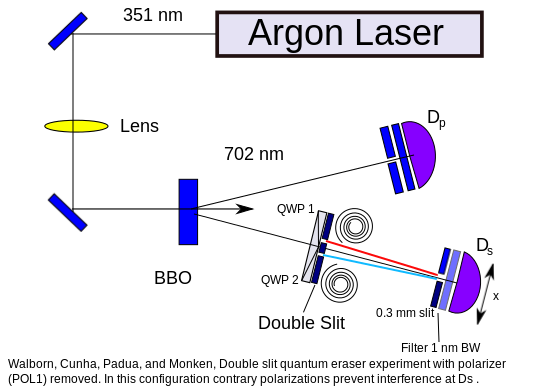
For a photon passing through a double slit, circular polarizers are placed in front of each slit, creating a clockwise polarization of light when passing through one slit, and counter-clockwise polarization when passing another slit. The photons passing through the polarizer in a clockwise direction cannot pass through the polarizer directed counterclockwise. And photons passing through the polarizer counterclockwise, respectively, can not pass through the polarizer directed clockwise. Circular polarizers "mark" photons, destroying the interference pattern on the second detector ( Fresnel-Arago laws ).

Next, a linear polarizer is introduced in the path of the first photon, which makes it possible to obtain diagonal polarization of photons. Entanglement also provides additional diagonal polarization in its partner, which passes through a double slit. This changes the effect of circular polarizers - now every photon is able to pass through circular polarizers in a clockwise and counterclockwise direction. Thus, it is no longer possible to determine by which path the photons have passed, and the interference fringes are restored.

Let's take a closer look at the following example. Imagine Alice using linear or circular polarization on the first detector, instantly influencing the measurement results of Bob on the second detector. Suppose that a BBO crystal produces the following state:


If Alice places a circular polarizer in front of the detector that filters clockwise polarized photons, then each time Alice measures a photon, the corresponding Bob photon necessarily has a clockwise polarization:


Since Bob has placed opposite polarization filters near each slit, we know that these photons can pass only (say) the first slit. From this slot, they fall on the screen in accordance with the wave function:


where a is the distance between the slits, d is the distance from the slits to the screen, and x is the distance to the middle of the screen. The intensity of light on the screen (number of photons) will be proportional to the square of the amplitude of this wave, in other words


Similarly, when Alice measures a photon with counterclockwise polarization, the corresponding photon of Bob is polarized counterclockwise, which can pass only through the second slit and hit the screen with the wave function


Note that the only difference is the a / 2 sign, because the photon was emitted from another slot. We will also see a spot on the screen - but this is another spot that is shifted a distance a . There is one important point: if Bob never knows what kind of polarization Alice applied, then Bob actually sees on his screen the sum of two intensities:


since both are produced in equal quantities by crystal. Bob can distinguish only two peaks in its data. Only after receiving Alice’s measurement results can he see that for a set of photons where Alice measured clockwise polarization, a subset of Bob’s photons was distributed according to a for a set of photons, where Alice measured counterclockwise polarization, a subset of Bob’s photons were distributed according to

(two peaks and their sum, when Alice measures the polarization of photons using a circular polarizer)

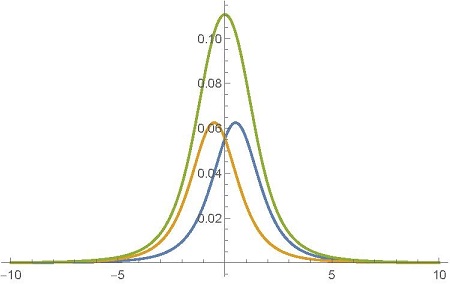
Now consider the situation where Alice uses a linear polarizer instead of a circular one. The first thing to do is to write the wave function of the system in terms of linear polarization states:


When Alice uses a horizontal polarizer, the Bob photon wave function will be in a state of superposition of polarization clockwise and counterclockwise. This means that the photon can really pass through both slots! If we hit the screen, we will get the wave amplitude

and its intensity

where is the phase difference between the two wave functions at position x on the screen. Now the screen is really an interference pattern! Similarly, if Alice uses a vertical polarizer, the amplitude of Bob’s photon waves is

and intensity

And again the interference pattern appears on the screen, but it has slightly changed from the previous one due to the phase difference of the photons intersecting the horizontal and vertical polarizer.

So can Alice send a message to Bob by coding her message using linear and circular polarizers? Unfortunately not. Since Bob was not told what polarization Alice had used, all he sees is the sum of two interferences. Therefore, the result


again is a stain.


(two interference patterns and their sum when Alice measures the polarization of photons with a linear polarizer) The

correlations change depending on which experiment Alice is conducting. Although the overall picture is the same, the two subsets ultimately produce radically different correlations: if Alice uses linear polarization, the full picture on the screen is formed from two interference patterns, and if Alice uses circular polarization, the picture is the sum of two peaks.

To detect the interference, it will be necessary to change this experiment as follows: instead of two slits with circular polarizers, it will be necessary to install a Mach Zehnder interferometer. Let us consider in more detail the principle of operation of this interferometer and try to find out what changes when using it.

INTERFEROMETER OF THE MAX TENDER
At the entrance of the interferometer there is a translucent mirror splitting the light flux into two beams. Reflecting from two opaque mirrors, they are brought together in the second translucent mirror. If a photon were a classical particle, then with a probability of 50% it could pass through the first translucent mirror, and with a probability of 50% it would reflect on it.
Suppose a photon has passed the first translucent mirror and moves along the lower branch. On the second translucent mirror, it can also pass or be reflected with a probability of 50%. That is, the contribution of the lower branch is as follows: 25% of the original number of photons will move up after the second translucent mirror and 25% down. If the photon reflected on the first translucent mirror and went along the upper branch, then on the second translucent mirror it, too, can either pass or be reflected. The contribution of the upper branch will also be 25% up and down. The overall probability is the sum of the contributions from the two branches and is 50% that the photon will move up after passing through the second translucent mirror and 50% down.

If we conduct a real experiment, we will see that all the photons passing through the device will move down. Not a single photon after the second translucent mirror will move up. The fact is that after passing through the first semi-transparent mirror, the photon will be described not by classical probabilities, but by quantum superposition.

Denote by base ket vectors with arrows two possible directions of photon motion: up and down. Then initially the photon will be described by the state of the "down". After passing through the first translucent mirror, the photon will be in a superposition of the basis vectors “up” and “down”. This superposition is another physical realization of the qubit, along with the electron spin and the photon polarization.
The squares of the absolute value of the amplitudes of the probabilities are just the classical probabilities of the passage and reflection of the photon. After the first translucent mirror they will coincide with the classical ones: 50% that the photon moves up and 50% that down. After passing through the second translucent mirror, the amplitudes of probability change their values. Moreover, within the framework of quantum mechanics, one can calculate that one of them will be equal to zero, and the other to one. That is, the photon will return to the state described by the base vector down. With one hundred percent probability after passing through the second translucent mirror, the photon will move down.

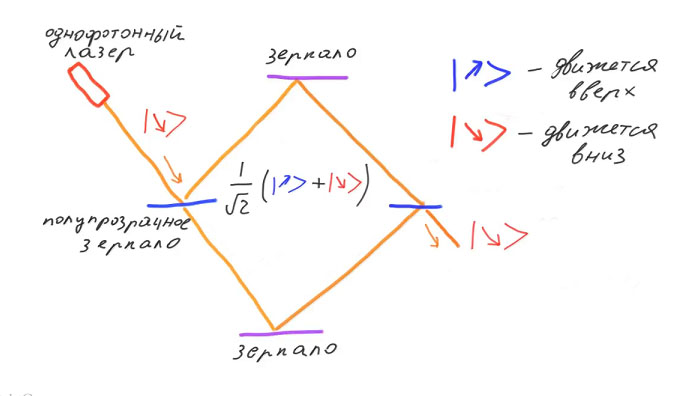
At the output of the second translucent mirror, nothing more than the interference of the photon with itself is observed. If we try to find out which of the interferometer arms actually passed the photon, then the interference disappears.

EXPERIMENT
Let us try to place circular polarizers in the Mach Zehnder interferometer. On one arm of the interferometer, we will install a circular polarizer clockwise. On the other shoulder we will install a circular polarizer counterclockwise. Moreover, on the upper shoulder a circular polarizer is installed directly after the translucent mirror. On the lower shoulder a circular polarizer is installed after the reflecting mirror. The fact is that a photon with circular polarization reflected from a mirror changes the direction of polarization to the opposite. Therefore, for photons that are not reflected from a translucent mirror, circular polarization is established after reflection from the mirror.
The presence of polarizers in the interferometer provides a potential opportunity to determine the path that the photon traveled. Therefore, the photon will pass either along the upper arm or along the lower arm, and will never pass through both shoulders at the same time. Accordingly, we do not observe interference at the output. The absence of interference leads to the fact that at the output we get 50% of photons directed upwards and 50% of photons directed downwards.

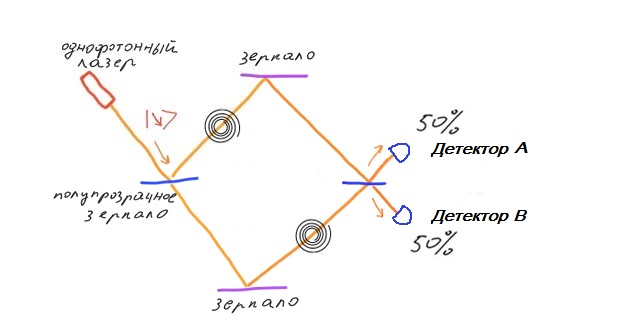
The situation will change if you use quantum-entangled particles. Suppose a laser beam hits a nonlinear optical device: a crystal of barium beta borate (BBO), due to which one photon is converted into two entangled photons of lower frequency. The resulting pair of photons will follow different paths, one of which passes a polarizer and goes directly to the detector 1, and the second passes through an interferometer with circular polarizers and hits detector 2 or 3 .
If we place a circular polarizer on the path of the first photon, we also will not see the interference. Accordingly, at the output we get 50% of photons directed upwards and 50% of photons directed downwards.
But if a linear polarizer located diagonally is placed on the path of the first photon, the entangled state will provide additional diagonal polarization in its partner. The presence of additional linear polarization will allow photons to pass through both arms and interfere with themselves. In this case, the interference will have a phase difference (photons, whose partners passed through a linear polarizer and whose partners did not pass, will create an interference on the screen that is offset from each other). Despite this, the photon at the exit from the second translucent mirror will return to the state described by the base vector down. Therefore, after passing through the second translucent mirror, all photons will move down.

Such a scheme of implementation is convenient because it does not require to establish a scheme of coincidence of entangled particles, release photons one by one and analyze the position of each photon on the screen. By installing or removing a linear polarizer in the path of entangled particles, you can instantly influence the distribution of their partners between detectors 2 and 3. It is enough to compare the intensity of the light flux in both detectors and determine the transmitted bit of information. Naturally, at the output of a BBO crystal, not all photons will turn out to be entangled. The number of tangled pairs will be several tens of percent of the total. But even a small change in the intensity of light can be detected by detectors, which will allow deciphering the transmitted information. The second big plus is that entangled pairs are not in a state of superposition between themselves.

RELATED CHALLENGES
The use of such schemes will allow to achieve a minimum delay in the transmission of information over long distances. The speed of information transfer can significantly exceed the speed of light in a vacuum. Some argue that the STO / GTR prohibits the transfer of information at a speed higher than the speed of light. The idea of ​​the finiteness of the speed of light was proposed by Poincare and derived from Maxwell’s formulas. In this case, initially it was about the electromagnetic field, and then with a light hand, Albert Germanovich was extended to all massive and massless material objects. It is important to emphasize that there was no talk about information. If you open any book on the Special Relativity / GTR, the information is not present in the mathematical formalism. Therefore, when it is argued that the CTO / GR prevents the transmission of information above the speed of light, an implicit assumption is made that except to “plant information” on a photon / electron beam, etc. does not exist.

PRINCIPLE OF CAUSE
One of the main problems of instant information transfer is a violation of the principle of causality. But it can be noted that modern physics does not anywhere require adherence to causality at the quantum level, so there is no physics among its postulates. There are quantum experiments in which the arrow of time may well be reversed. However, a person cannot refuse adherence to causality, since this is contrary to our logic.

According to Einstein’s theory of relativity, the instantaneous transmission of information allows information to be obtained before it is sent. For example, if we decide to send information to ourselves, then we can conduct an experiment in such a way as to obtain information before we send it. Assume that we will transmit information using a confusing pair. Then one photon will pass through the interferometer and fall on the detector, and the second photon, for example, will go to the Moon, where it will reflect from the mirror and return to us.
By installing or removing a linear polarizer in the path of the second photon, we can influence the result at the output of the interferometer. So, watching the detectors at the output of the interferometer, we will know in advance what information we decide to send in 2.5 seconds (the flight time of photons to the Moon and back). This can lead to the “paradox of the murdered grandfather,” when we saw one meaning and decided to send the opposite.

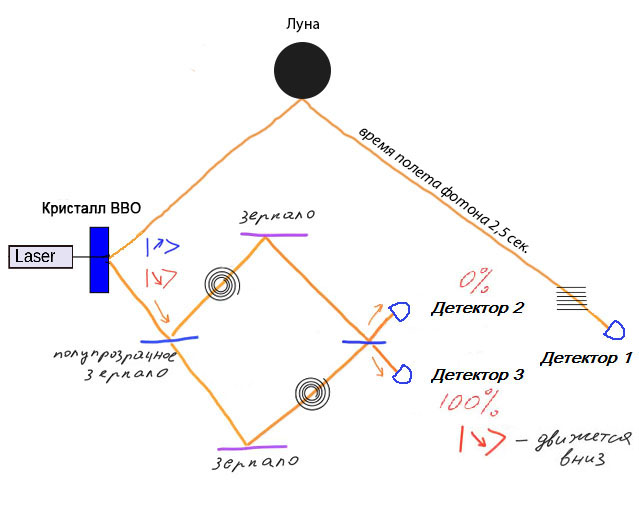
This problem can be solved by the theory of alternative realities by Hugh Everett, who today has many supporters. According to Everett's theory, there are countless alternative realities. With each choice opportunity, our reality is divided into several alternative realities, in which all possible choices are realized. Reality can intersect and diverge, forming a variety of options for the past and future.

According to this theory, the interference on two slits is the intersection of two similar realities without any collapse of the wave function. In one reality, the photon passed through the first slit, in another reality, the photon passed through the second slit. At the intersection of two realities, it turns out that the photon passed through both slits. We can’t find out what kind of slit the photon went through, because the past of the photon is uncertain for us. The same applies to the future. After the emission of a photon, we cannot know where it is. A photon can be located anywhere, and in each version of the future one of the probabilities is realized, where the photon's trajectory is precisely defined.

If Hugh Everett's theory is correct, then our decision to send the opposite value instead of what we saw will not lead to the "paradox of the murdered grandfather." In this case, we will see on the screen only the average of the two possible options, according to which we can no longer determine what information we decided to send to ourselves in the future. We can send any option and it will not cause any problems.

Conducting real experiments, perhaps, will allow us to obtain experimental confirmation of this theory. Although indirect confirmation of the theory already exists. For example, it is possible to obtain a photograph of microscopic objects without disturbing the object under study (that is, without sending a single photon to the object). This phenomenon is being actively studied in order to build new types of microscopes.

ENTROPY
As we know, entropy is a measure of disorder. It is believed that the passage of time leads to an increase in entropy. Hence, the past must have less entropy than the future. And if we try to return to the past, this will lead to the problem of increased entropy. In fact, entropy has nothing to do with the transfer of information, since we do not send any material bodies to the past. Therefore, the problem of the increased entropy of thermodynamic systems cannot be applied to photons.

ANALYSIS OF THE FUTURE
The theory of multi-world interpretation does not mean that there is no way to obtain reliable information from the future. Using the above scheme in deterministic systems will allow to obtain a reliable forecast with a high degree of probability. For example, if we decide to find out if the moon will disappear tomorrow, then in many alternative scenarios (diverging from our reality today), this probability will be minimal. Accordingly, the results of the experiment will indicate primarily one answer. You can also get a weather forecast with a high degree of confidence, bypassing the huge amount of computing in supercomputers. The possibilities of application in the field of forecasting are very large. One of the important tasks for the analysis can be the prediction of the most important decisions (for example, the beginning of hostilities, and

It should be noted that the real use in the field of forecasting the future is still far. To get a day delay, you need to bring a dielectric mirror to the border of the solar system, and make a very high-quality laser with a minimum angle of divergence. If you use multiple beam reflections, you will need to create perfectly reflective dielectric mirrors. For example, a day will have 70,000 times to repulse a laser beam between the Earth and the Moon. Perhaps the solution will be to slow down the speed of light using a super-cooled medium known as Bose-Einstein condensate. As far as I know, physicists from the Rowland Institute for Scientific Research managed to slow down the speed of light to 17 meters per second.a few years later a group of scientists from Harvard University even managed to completely stop the light for 10-20 ms.

Sources:
Quantum eraser experiment
Interference of a qubit with itself.
Is multidimensional real?