Quantum mechanics for all, for nothing, and let no one go offended: part two
- Transfer
- Recovery mode
Hello! Quantum mechanics continues in the second part of the Eliezer Yudkowski cycle, and today you will learn a little more about configurations, as well as understand why the observation process affects the observation object. Criticism of the slow-witted humanity, by itself, will also be plenty. In general, do not pass by!
← read the first part
One of the key points in quantum mechanics is that configurations always describe the state of more than one particle. Look: this time we have a little complicate the experiment from the first article, at the same time sending two photon to D - from the point B and the C .
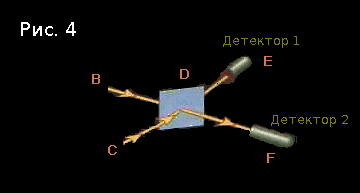
The initial configuration is “the photon flies from B to D , and the photon flies from C to D ”. As last time, we assume that its amplitude is (-1 + 0 i ).
In D there is a half-silvered mirror already familiar to us, which multiplies the amplitude by 1 when the photon is reflected, and by - i- during the passage of a photon (in the original it was i , but this is not entirely true - approx. Per. ).
Consider four cases:
Please note that completely different situations in the first and fourth cases led to the same resulting configuration! Therefore, when we consider the final value of the configuration “the photon flies in E and the photon flies in F ”, we get (1 + 0 i ) + (−1 + 0 i ) = 0. And this means that this will never happen . Both detectors cannot work simultaneously.
One important lesson to be learned from this experiment: photons are indistinguishable . If there was even the slightest difference between the two photons, the result of the experiment would be completely different.
In the classical model of the world, where amplitudes can be considered probabilities, everyone is free to choose the method of grouping outcomes. Let me explain: I could consider all four outcomes described above to be different; could distinguish only two outcomes (“each photon arrives at a photon” and “both photons arrive at a single detector”); could do something else. And nothing would have changed. In the same way, if I need to calculate the probability that odd numbers will fall out on two dice, I can make a plate of 36 possible results of the throw - but I can immediately divide the edges into “even” and “odd” and reduce the number of outcomes to four.
Why does this not work in the quantum model? Because the probabilities of events non-linearly depend on the amplitudes, and the square of the sum, as you know, cannot be replaced by the sum of squares:
It follows from this that we can experimentally establish which configurations are different and which are not. In particular, these configurations are identical:
And here is the second important lesson (which I hinted at in the first paragraph, and which I will discuss in detail later): the laws of quantum mechanics are not applicable to individual particles . The divide and conquer strategy does not work here. It is a great temptation to consider the behavior of each elementary particle without any particular difficulties, and then to somehow compose an integral picture of the world from pieces of mosaics ... But it was this approach that had hindered the development of quantum mechanics for so many years.
Immediately take the bull by the horns. When are the two configurations different?
To answer this question, we will conduct the following experiment:

At point S is a sensor. The only thing he does is goes into another state when a photon passes through it. We assume that at the beginning of the experiment the sensor is in a state
So, the initial configuration:
What happens after a photon arrives at A ? In the previous version of this experiment — without a sensor — the possible configurations were “photon flies from A to B ” with amplitude i and “photon flies from A to C ” with amplitude −1. But since each configuration describes the complete state of the system, we must include the state of the sensor in their descriptions. So:
Now mirrors B and C come into play :
Finally, the semi-mirror D :
Remember: when we conducted this experiment without a sensor , outcomes # 1 and # 3 “neutralized” each other, because the configurations corresponding to them were identical. But now they are not identical - and all thanks to the S sensor . The squares of the amplitude modules of all four configurations are equal, and if you actually conducted this experiment, you would make sure that both detectors operate at the same frequency. ( If I didn’t mess up anything, of course. Personally, I did not conduct any experiment.)
The same will happen if we are not indifferent to the state of the sensor. The laws of physics are just as indifferent to our thoughts.
The same would happen if we did not even bother to check if the photon went through the S . Configurations # 1 and # 3 are different - nothing else is needed.
The same will happen if we do not know about the existence of S at all .
The same will happen if the experiment is carried out in space, and S signals its state by sending a single photon in one direction if it was in a state
(But the same will not happen if S has a sufficiently large extent in the configuration space. In this case, the action of a photon on Smay not be enough to form a separate outcome. I just wanted to remind you that in fact the configuration space is continuous, not discrete.)
And now let's try to imagine what a person who is doing an experiment like this is thinking if he has no idea about the amplitudes and configurations.
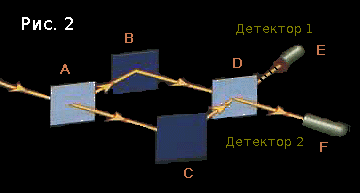
Our experimenter discovers that a) photons do not want to come to the first detector, and b) photons suddenly begin to come to both detectors if one of the paths is blocked, but they are never separated. Hm.
Firstly, he believes that he is dealing with particles - because all that he observes is individual photons, each of which is located (as he believes) in a strictly defined position at each moment in time. This is logical, although false.
Secondly, he is sure of the existence of a certain ... mysterious phenomenon ... which does not allow the photon to appear in the first detector. For this, it is imperative that the photonhad the opportunity to be in any of the detectors. Even if in the end he always chooses the second.
The cunning photon not only wants to not be obstructed - he also knows that the path is blocked, even without walking along it . What the hell is going on here?
Our experimenter decides to place the sensor between A and C in order to track which path the photon chooses each time.

And the mysterious phenomenon was blown away by the wind.
From this and become paranoid for long.
In the twenty-first century, we already realized that “knowing” what happened to the photon is tantamount to changing the position of the septillonsparticles in our brain. If even one photon emitted by the sensor in an unknown direction is enough to make the configurations different and prevent the reduction in amplitudes, then the sophisticated measuring device with which we will catch the photon is definitely enough.
But if you haven’t thought of all this, your affairs are bad. Your thoughts are likely to go in a slightly different direction.
A photon does not just want to have the physical ability to go both ways - the sensor is completely transparent to it. Everything is much worse. The photon does not want you to know where he is and what he is doing.
If you know exactly what the photon flew here , all other possibilities will become somewhatimplausible . This interferes with the photon no less than a real obstacle in its path. The important thing is not what happened, but what could happen. What you know - or rather, what you theoretically can know - is a determining factor.
Urgent in the room! Conscious understanding can influence experimental results! Reason is still primary!
Nah yes. Was it really so hard to notice that a simple stone “observing” the course of the experiment has the same effect on it? Perhaps the stones also have a consciousness?
However, in hindsight, everyone is smart. Don't you think that you would do better than John von Neumann if you lived at that time? The main thing then was that the theory, albeit delusional, gave true predictions; do not repair what is not broken, and everything will be fine.
← read the first part
← read the first part
Configurations as Combinations
One of the key points in quantum mechanics is that configurations always describe the state of more than one particle. Look: this time we have a little complicate the experiment from the first article, at the same time sending two photon to D - from the point B and the C .

The initial configuration is “the photon flies from B to D , and the photon flies from C to D ”. As last time, we assume that its amplitude is (-1 + 0 i ).
In D there is a half-silvered mirror already familiar to us, which multiplies the amplitude by 1 when the photon is reflected, and by - i- during the passage of a photon (in the original it was i , but this is not entirely true - approx. Per. ).
Consider four cases:
- Both photons were reflected. The amplitude equal to (−1 + 0 i ) × - i × - i = (1 + 0 i ) is taken into account the configuration “the photon flies from D to E , and the photon flies from D to F ”.
- A photon flying from B reflected; a photon flying from C flew by. The amplitude equal to (−1 + 0 i ) × - i × 1 = (0 + i ) is taken into account the configuration “two photons fly from D to E ”.
- A photon flying from B flew by; a photon flying from C is reflected. The amplitude equal to (−1 + 0 i ) × 1 × - i = (0 + i ) is taken into account the configuration “two photons fly from D to F ”.
- Both photons flew by. The amplitude equal to (−1 + 0 i ) × 1 × 1 = (−1 + 0 i ) is taken into account the configuration “the photon flies from D to E and the photon flies from D to F ”.
Please note that completely different situations in the first and fourth cases led to the same resulting configuration! Therefore, when we consider the final value of the configuration “the photon flies in E and the photon flies in F ”, we get (1 + 0 i ) + (−1 + 0 i ) = 0. And this means that this will never happen . Both detectors cannot work simultaneously.
One important lesson to be learned from this experiment: photons are indistinguishable . If there was even the slightest difference between the two photons, the result of the experiment would be completely different.
In the classical model of the world, where amplitudes can be considered probabilities, everyone is free to choose the method of grouping outcomes. Let me explain: I could consider all four outcomes described above to be different; could distinguish only two outcomes (“each photon arrives at a photon” and “both photons arrive at a single detector”); could do something else. And nothing would have changed. In the same way, if I need to calculate the probability that odd numbers will fall out on two dice, I can make a plate of 36 possible results of the throw - but I can immediately divide the edges into “even” and “odd” and reduce the number of outcomes to four.
Why does this not work in the quantum model? Because the probabilities of events non-linearly depend on the amplitudes, and the square of the sum, as you know, cannot be replaced by the sum of squares:
((2 + i ) + (1 + - i )) 2 = (3 + 0 i ) 2 = 3 2 + 0 2 = 9
(2 + i ) 2 + (1 + - i ) 2 = (2 2 + 1 2 ) + (1 2 + (−1) 2 ) = (4 + 1) + (1 + 1) = 7
It follows from this that we can experimentally establish which configurations are different and which are not. In particular, these configurations are identical:
- “A photon from B is reflected in D and flies in E ; photon C is reflected in D and flies in F ";
- “A photon from B flies through D to E ; photon C flies through D to F ".
And here is the second important lesson (which I hinted at in the first paragraph, and which I will discuss in detail later): the laws of quantum mechanics are not applicable to individual particles . The divide and conquer strategy does not work here. It is a great temptation to consider the behavior of each elementary particle without any particular difficulties, and then to somehow compose an integral picture of the world from pieces of mosaics ... But it was this approach that had hindered the development of quantum mechanics for so many years.
Various configurations
Immediately take the bull by the horns. When are the two configurations different?
To answer this question, we will conduct the following experiment:

At point S is a sensor. The only thing he does is goes into another state when a photon passes through it. We assume that at the beginning of the experiment the sensor is in a state
НЕТ, and a passing photon brings it into a state ДА. So, the initial configuration:
- “The photon flies towards A ; S in the state
НЕТ”= (−1 + 0 i )
What happens after a photon arrives at A ? In the previous version of this experiment — without a sensor — the possible configurations were “photon flies from A to B ” with amplitude i and “photon flies from A to C ” with amplitude −1. But since each configuration describes the complete state of the system, we must include the state of the sensor in their descriptions. So:
- “The photon flies from A to B ; S in the state
НЕТ"= (0 + i ) - “The photon flies from A to C ; S in the state
ДА”= (−1 + 0 i )
Now mirrors B and C come into play :
- “The photon flies from B to D ; S in the state
НЕТ”= (−1 + 0 i ) - “The photon flies from C to D ; S in the state
ДА"= (0 + i )
Finally, the semi-mirror D :
- “The photon flies from D to E ; S in the state
НЕТ"= (0 + i ) - “The photon flies from D to F ; S in the state
НЕТ”= (−1 + 0 i ) - “The photon flies from D to E ; S in the state
ДА"= (0 + i ) - “The photon flies from D to F ; S in the state
ДА"= (1 + 0 i )
Remember: when we conducted this experiment without a sensor , outcomes # 1 and # 3 “neutralized” each other, because the configurations corresponding to them were identical. But now they are not identical - and all thanks to the S sensor . The squares of the amplitude modules of all four configurations are equal, and if you actually conducted this experiment, you would make sure that both detectors operate at the same frequency. ( If I didn’t mess up anything, of course. Personally, I did not conduct any experiment.)
The same will happen if we are not indifferent to the state of the sensor. The laws of physics are just as indifferent to our thoughts.
The same would happen if we did not even bother to check if the photon went through the S . Configurations # 1 and # 3 are different - nothing else is needed.
The same will happen if we do not know about the existence of S at all .
The same will happen if the experiment is carried out in space, and S signals its state by sending a single photon in one direction if it was in a state
ДА, and in the other if it was in a state НЕТ. For us it is all the same that it is not; but one particle in the whole Universe is in another place, and that’s enough. (But the same will not happen if S has a sufficiently large extent in the configuration space. In this case, the action of a photon on Smay not be enough to form a separate outcome. I just wanted to remind you that in fact the configuration space is continuous, not discrete.)
And now let's try to imagine what a person who is doing an experiment like this is thinking if he has no idea about the amplitudes and configurations.

Our experimenter discovers that a) photons do not want to come to the first detector, and b) photons suddenly begin to come to both detectors if one of the paths is blocked, but they are never separated. Hm.
Firstly, he believes that he is dealing with particles - because all that he observes is individual photons, each of which is located (as he believes) in a strictly defined position at each moment in time. This is logical, although false.
Secondly, he is sure of the existence of a certain ... mysterious phenomenon ... which does not allow the photon to appear in the first detector. For this, it is imperative that the photonhad the opportunity to be in any of the detectors. Even if in the end he always chooses the second.
The cunning photon not only wants to not be obstructed - he also knows that the path is blocked, even without walking along it . What the hell is going on here?
Our experimenter decides to place the sensor between A and C in order to track which path the photon chooses each time.

And the mysterious phenomenon was blown away by the wind.
From this and become paranoid for long.
In the twenty-first century, we already realized that “knowing” what happened to the photon is tantamount to changing the position of the septillonsparticles in our brain. If even one photon emitted by the sensor in an unknown direction is enough to make the configurations different and prevent the reduction in amplitudes, then the sophisticated measuring device with which we will catch the photon is definitely enough.
But if you haven’t thought of all this, your affairs are bad. Your thoughts are likely to go in a slightly different direction.
A photon does not just want to have the physical ability to go both ways - the sensor is completely transparent to it. Everything is much worse. The photon does not want you to know where he is and what he is doing.
If you know exactly what the photon flew here , all other possibilities will become somewhatimplausible . This interferes with the photon no less than a real obstacle in its path. The important thing is not what happened, but what could happen. What you know - or rather, what you theoretically can know - is a determining factor.
Urgent in the room! Conscious understanding can influence experimental results! Reason is still primary!
Nah yes. Was it really so hard to notice that a simple stone “observing” the course of the experiment has the same effect on it? Perhaps the stones also have a consciousness?
However, in hindsight, everyone is smart. Don't you think that you would do better than John von Neumann if you lived at that time? The main thing then was that the theory, albeit delusional, gave true predictions; do not repair what is not broken, and everything will be fine.
← read the first part
