March 13, 2013 at 23:04

Building an optical recognition system for structural information using the example of Imago OCR

    In this note, I will talk about how you can build an optical recognition system for structural information based on the algorithms used in image processing and their implementation in the framework of the OpenCV library. Behind the description of the system is the actively developing open source project Imago OCR , which can be directly useful in the recognition of chemical structures , but in this article I will not talk about chemistry, but I will touch on more general issues, the solution of which will help in the recognition of structured information of various kinds, for example, tables or graphics.

    Recognition Engine Structure


    One of the most common options for displaying the structure of the engine of the optical recognition system can be selected as follows:

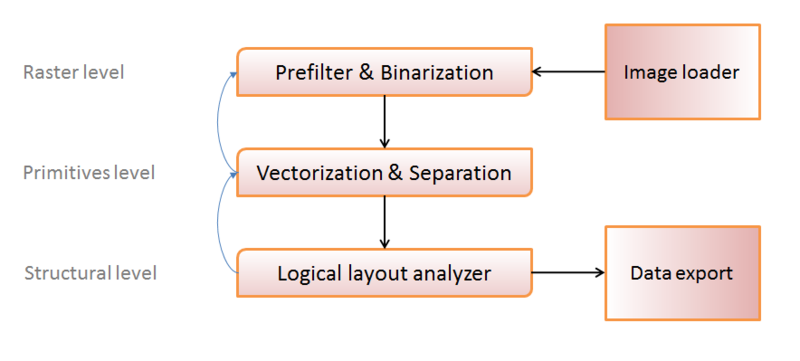
    Conventionally, processing methods can be divided into three levels:
    • Raster level (working with a set of image pixels);
    • Level of primitives (we identify groups of pixels with certain primitives - symbols, lines, circles, etc.);
    • Structural level (we collect groups of primitives into logical units - “table”, “table cell”, “label”, etc.)

    With black arrows I depicted the main direction of data transfer: we load an image, convert it to a convenient form for processing, get primitives, organize primitives into structures, write the result.

    Blue arrows represent “feedback” - in some cases it becomes impossible to recognize an object at a certain level (to assemble at least some logically acceptable structure from primitives, or to isolate at least some primitive from a set of points). This indicates either a “bad” original image or an error in the previous step, and to avoid such errors, we try to process the object again, possibly with other parameters, at the previous structural level.

    At this stage, we will not go into details, but this makes optical recognition systems of structural information significantly different from “general recognition” - we have the opportunity to correct some errors by understanding the necessary output structure. This circumstance slightly changes the approach to the construction of particular recognition methods, making it possible to create adaptive algorithms that depend on some tolerances that are changed during processing and have quality metrics that can be calculated at the stage of structural processing.

    Raster Level: Image Download


    Since we used the wonderful OpenCV library , this step is as simple as possible. OpenCV can load many popular raster formats: PNG, JPG, BMP, DIB, TIFF, PBM, RAS, EXR, and in fact in one line:
    cv::Mat mat = cv::imread(fname, CV_LOAD_IMAGE_GRAYSCALE);

    The selected CV_LOAD_IMAGE_GRAYSCALE parameter allows you to upload a picture in the form of a matrix of pixel intensities (the conversion to grayscale will happen automatically). In some tasks it is necessary to use color information, but in ours it is not necessary, which allows to significantly save memory allocation. Of the tricks, except that the loading of “transparent” PNGs, the transparent background will be interpreted as black, which can easily be done by loading with the CV_LOAD_IMAGE_UNCHANGED parameter and manually processing the BGRA color information (yes, OpenCV stores color data in this order).

    Let at this stage we get something like this:
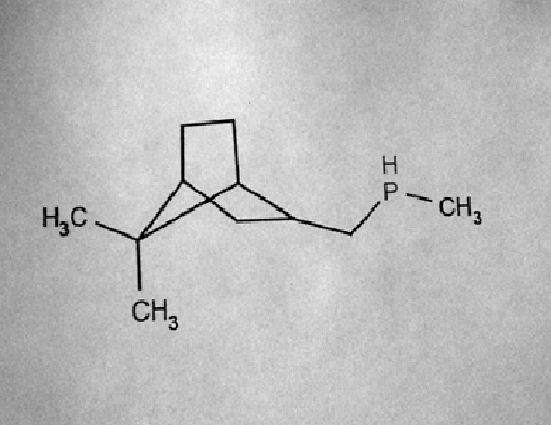
    I deliberately chose the picture “worse” to show that optical recognition is associated with many difficulties that we will solve further, but it is from “real life” - mobile phone cameras “and not that”.

    Raster Level: Pre-Filtering


    The main task of pre-filtering is to improve the "quality" of the image: to remove noise, without loss in detail and restore contrast.

    Armed with a graphical editor, you can figure out a lot of tricky schemes on how to improve image quality, but here it is important to understand the boundary between what can be done automatically and what is fiction, applicable to exactly one image. Here are examples of more or less automated approaches: sparse masks , median filters , for those who like to google .

    I would like to compare methods, and showwhy we chose a certain one, but in practice it’s difficult. In various images, certain methods have their advantages and disadvantages, on average there is no better solution, therefore, in Imago OCR we designed a stack of filters, each of which can be applied in certain cases, and the choice of the result will depend on the quality metric.

    But I want to talk about one interesting solution: Retinex Poisson Equation.

    The advantages of the method include:
    • Pretty high speed;
    • Parameterizable quality of the result;
    • Lack of erosion during work, and as a result, “sensitivity” to details;
    • And the main interesting feature is the normalization of local levels of illumination.

    The last property is perfectly illustrated by the image from the article, and it is important for recognition because of the possible heterogeneity of illumination of objects when shooting (a piece of paper turned to the light source so that the light falls unevenly):


    Surface description of the algorithm:
    • Local threshold image filtering ( laplacian threshold ) with threshold T;
    • Discrete cosine transform of the received image;
    • Filtering high-frequency characteristics and solving a special equation for low and medium frequencies (Retinex Equation);
    • Inverse discrete cosine transform.

    The algorithm itself is rather sensitive to the parameter T, but we used its adaptation:
    • We consider Retinex (T) for T = 1,2,4,8
    • Per-pixel median filtering between Retinex results
    • Normalize contrast

    How OpenCV will help: there is a ready-made function for computing a discrete cosine transform:
    void dct(const Mat& src, Mat& dst, int flags=0); // flags = DCT_INVERSE for inverse DCT

    And it works no worse in speed than the analogous one from libfftw, although I don’t presume to say this in the general case (tested on Core i5, Core Duo).

    For the original image, the above method gives a pretty nice result:


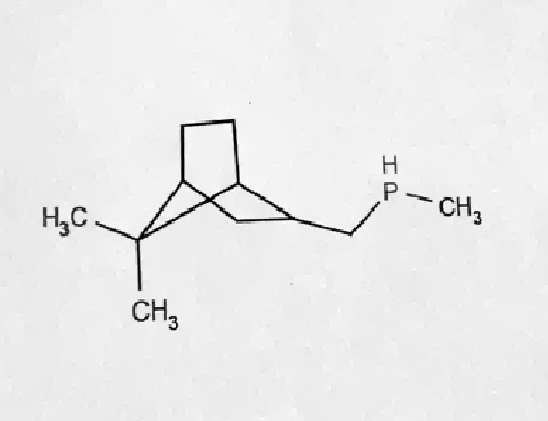
    Now we understand roughly what preliminary filtering should do, and we already have one parameter that can change in the feedback mechanism: the index of the filter used .

    Hereinafter : in fact, of course, there are many other parameters (for example, the same ones, “magic” T = 1,2,4,8), but in order not to “boggle your head”, we will not talk about them now. There are many of them, references to them will pop up in the section on machine learning, but I will omit the specifics so as not to overload the presentation with the number of parameters.

    Raster Level: Binarization


    The next step is to obtain a black and white image, where black will correspond to the presence of “paint”, and white to its absence. This is done because a number of algorithms, for example, obtaining the contour of an object, do not constructively work with halftones. One of the simplest binarization methods is threshold filtering (we select t as the threshold value, all pixels with intensity greater than t are the background, less are “paint”), but due to its low adaptability, the otsu threshold or adaptive gaussian threshold is more often used .

    Despite the adaptability of more advanced methods, they still contain threshold values ​​that determine the "amount" of output information. In the case of more stringent thresholds - some of the elements may be lost, in the case of “soft” ones - “noise” may come out.
    Strong thresholdingWeak thresholding

    You can try to accurately guess the thresholds for each image, but we went the other way - we used the correlation between the received images with different adaptive binarization thresholds:
    • We consider strong and weak binarization (with given thresholds t1 and t2);
    • We break the images into a set of connected pixel-by-pixel regions ( marking segments );
    • We remove all the “weak” segments that have a correlation with the corresponding strong ones, less than the given (cratio);
    • We remove all the "weak" segments of low density (the proportion of black / white pixels is less than the specified bwratio);
    • The remaining “weak” segments are the result of binarization.

    As a result, in most cases we get an image devoid of noise and without loss in detail:

    The described solution may look strange in the light of the fact that we wanted to “get rid” of one parameter, but introduced a whole bunch of others, but the main idea is that the correctness binarization is now ensured if the “real” binarization threshold falls into the interval between the t1 and t2 chosen by us (although we cannot “infinitely” increase this interval, there is also a restriction on the difference t1 and t2).

    The idea is quite viable when applied with various threshold filtering methods, and OpenCV “helped” by the presence of built-in adaptive filtering functions:
    cv::adaptiveThreshold(image, strongBinarized, 255, cv::ADAPTIVE_THRESH_GAUSSIAN_C, CV_THRESH_BINARY, strongBinarizeKernelSize, strongBinarizeTreshold);
cv::threshold(image, otsuBinarized, otsuThresholdValue, 255, cv::THRESH_OTSU);

    If the final image does not contain segments at all, then a filtering error has probably occurred and it is worth considering another preliminary filter (“feedback”; “the same” blue arrows in the image of the engine structure).

    Primitive Level: Vectorization


    The next step in the recognition process is the conversion of sets of pixels (segments) into primitives. Primitives can be figures - a circle, a set of segments, a rectangle (a specific set of primitives depends on the problem being solved), or symbols.

    While we do not know which class each object belongs to, we are therefore trying to vectorize it in various ways. The same set of pixels can be successfully vectorized both as a set of segments and as a symbol, for example, "N", "I". Or the circle and symbol are “O”. At this stage, we do not need to know reliably which class the object has, but we need to have a certain metric of similarity of the object with its vectorization in a certain class. This is usually solved by a set of recognizing functions.

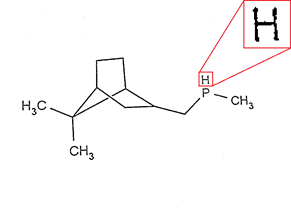
    For example, for a set of pixels we will get a set of the following objects (do not think about specific numbers of the metric, they are given to represent what we want from the recognition process, but they themselves do not make sense yet):
    • vectorization in the form of the “H” symbol with a metric (distance) value of 0.1 (maybe this is exactly H) ;
    • vectorization in the form of the symbol “R” with a metric value of 4.93 (unlikely, but it is possible that R is also) ;
    • vectorization in the form of three segments "|", "-", "|" with a metric value of 0.12 (it is possible that these are three segments) ;
    • vectorization as a rectangle with x, y side dimensions with a metric value of 45.4 (not at all like a rectangle) ;
    • vectorization as a circle with metric value + inf (guaranteed is not a circle) ;
    • ...

    In order to get a list of vectorizations, it is necessary to implement recognition primitives for each particular class.

    Segment Set Recognition

    Typically, a raster region is vectorized into a set of segments as follows:
    • Performing a thinning filter ( -> );
    • Segmentation (decorner) ( );
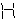    • Approximation of points of each segment;
    • The result is a set of approximations and a deviation of the approximation from the original.

    There is no ready-made thinning filter in OpenCV, but it is not at all difficult to implement it . Segmentation (decorner), too, but this is completely trivial: we throw out all the points from the region that have more than two neighbors. But the approximation of points as a set of segments in OpenCV is present, and we used it:
    cv::approxPolyDP(curve, approxCurve, approxEps, closed); // approximation of curve -> approxCurve

    An important parameter is the approximation tolerance ( approxEps ), with an increase in which we get a larger number of segments as a result, and with a decrease - a coarser approximation, and, as a result, a larger metric value. How to choose it right ?

    Firstly, it strongly depends on the average line thickness (intuitively - the larger the line thickness, the less detail; the drawing drawn with a sharp pencil can be much more detailed than that drawn with a marker), which we used in our implementation:
    approxEps = averageLineThickness * magicLineVectorizationFactor;

    Secondly, taking into account the above approach to the classification of objects, it is possible to try to vectorize segments with different approxEps (with a certain step) and choose “more suitable” already at the stage of analyzing the logical structure.

    Circle recognition

    Pretty simple:
    • We are looking for the center of the circle (average over the coordinates of the points) - (x, y);
    • We are looking for the radius (the average distance of points from the center) - r;
    • We consider the error: the average distance by points to a circle with center (x, y) and radius r and thickness averageLineThickness;
    • We consider an additional penalty for circle breaks: magicCirclePenalty * (% of breaks).

    After selecting magicCirclePenalty there were absolutely no problems with this code, as well as with rectangle recognition similar to it.

    Character recognition

    A much more interesting part, as this is a challenge problem - there is not a single algorithm that claims to be the “most optimal” recognition indicators. There are very simple methods based on heuristics , there are more complex ones, for example, using neural networks , but none guarantee a “good” quality of recognition.

    Therefore, the decision to use several subsystems of character recognition and the choice of aggregate result seemed quite natural: if p1 = the metric value of the fact that, by algorithm 1, region A is recognized as the symbol s, and p2 = the metric value of what algorithm 2 recognizes region A as the symbol s, then final value p = f (p1, p2). We have chosen two algorithms with conveniently comparable values, high speed and sufficient stability:
    • recognition based on Fourier descriptors;
    • masks of quadratic deviation of points.

    Character recognition based on Fourier descriptors

    Training:
    • Getting the external contour of the object;
    • Transformation of coordinates of contour points (x; y) into complex numbers x + iy;
    • The discrete Fourier transform of the set of these numbers;
    • The rejection of the high-frequency part of the spectrum.

    When performing the inverse Fourier transform, we obtain a set of points that describes the initial figure with a given degree of approximation (N is the number of coefficients left):


    The “recognition” operation consists in calculating Fourier descriptors for the recognized region and comparing them with predefined sets that are responsible for the supported characters. To get the metric value from two sets of descriptors, you need to perform an operation called convolution: d = sum ((d1 [i] -d2 [i]) * w [i], i = 1, N), where d1 and d2 are sets of descriptors Fourier, and w is the weight vector for each coefficient (we got it by machine learning). The convolution value is invariant with respect to the scale of the compared symbols. In addition, the function is resistant to high-frequency noise (random pixels that do not change the "geometry" of the figure).

    OpenCV helps pretty much in implementing this method; There is a ready-made function for obtaining the external contours of objects:
    cv::findContours(image, storage, CV_RETR_EXTERNAL);

    And there is a function for computing the discrete Fourier transform:
    cv::dft(src, dst);

    It remains only to implement convolution and intermediate type conversions, saving a set of descriptors.

    The method is good for handwritten characters (probably because some others give less high-quality results against it), however, it is poorly suited for low-resolution characters due to the fact that high-frequency noise, that is, “extra” pixels become large in relation to the whole image and begin to influence those coefficients that we do not discard. You can try to reduce the number of compared coefficients, but then it becomes more difficult to make a choice of similar small characters. And so another recognition method was introduced.

    Character recognition based on quadratic deviation masks

    This is a pretty intuitive solution, which, as it turned out, works great for printed characters of any resolution; if we have two black and white images of the same resolution, then we can learn to compare them pixel by pixel.

    For each point in Image 1, a penalty is considered: the minimum distance to Image 2 in the same color. Accordingly, a metric is simply the sum of fines with a normalizing coefficient. Such a method will be much more stable on small-resolution images with noise: for an image with side length n, individual pixels up to k percent will not “spoil” a metric of more than k * n in the worst case, and in practical cases, by no more than k , because in most cases they are adjacent to the "correct" pixels of the image.

    The disadvantage of the method, as I described, will be low speed. For each pixel (O (n 2 )), we consider the minimum distance to a pixel of the same color of another picture (O (n 2 )), which gives O (n 4 ).

    But this is quite easily treated by precomputing: we will build two masks penalty_white (x, y) and penalty_black (x, y) in which the calculated fines will be stored for the pixel (x, y) being white or black, respectively. Then the process of “recognition” (that is, calculation of the metric) fits into O (n 2 ):
    for (int y = 0; y < img.cols; y++)
{
	for (int x = 0; x < img.rows; x++)
	{
		penalty += (image(y,x) == BLACK) ? penalty_black(y,x) : penalty_white(y,x);
	}
}

    All that remains is to store the masks (penalty_white, penalty_black) for each spelling of each character and iterate over them in the process of recognition. OpenCV will hardly help us in implementing this algorithm, but it is trivial. But, as I already said, the images to be compared must be of the same resolution, so to bring one to another, you may need a function:
    cv::resize(temp, temp, cv::Size(size_x, size_y), 0.0, 0.0);

    If we return to the general process of character recognition, then as a result of running both methods we get a table of metric values:

    The recognition value is not one element, but the whole table from which we know that with the highest probability it is the character “C”, but it’s possible it is “0”, or “6” (or “O”, or “c” that did not fit on the screen). And if it is a bracket, then it is more likely to open than close. But for now, we don’t even know if this is a symbol at all ...

    Primitive Level: Separation


    If we lived in an ideal world of superproductive (quantum?) Computers, then most likely this step would not be necessary: ​​we have a set of some objects, for each of which there is a table of “probabilities” that determines what exactly it is. We sort through all the elements in the table for each object, build a logical structure, and select the most probable (by the sum of the metrics of individual objects) from the valid ones. Business, except perhaps the exponential complexity of the algorithm.

    But in practice, it is usually required to determine the type of an object by default. That is, to choose some ready-made interpretation of objects in the image, and then, it is possible to slightly change it. Why couldn’t we choose the type of objects in the previous step (vectorization)? We did not have enough statistical information about all the objects, and if we treat a certain set of pixels in isolation from the whole picture, then reliably determining its meaning becomes problematic.

    This is one of the most important issues in recognizing structural information. Everything is much better for a person with this than for a car, because he simply does not know how to see pixels separately. And one of the initial stages of disappointment in building an OCR system is an attempt to algorithmize a seemingly human approach “in steps” and to obtain unsatisfactory results. It seems that right now, it is worth improving the recognition algorithms of primitives a bit so that they are not “mistaken”, and we will get better results, but there are always a few pictures that “break” any logic.

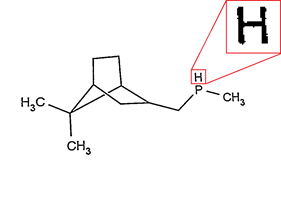
    And so, we ask the person what it is -
    Of course, this is just a curved line. But if you need to rank it either as symbols or as a set of straight line segments, then what is it? Then it is most likely either the letter “l” or two straight lines at an angle (just the corner is drawn rounded). But how to choose the right interpretation? The machine at the previous step could also solve an approximate problem, and solve it correctly with a probability of 1/2. But 1/2 is a complete collapse for the structural information recognition system, we will just ruin the structure, it will not pass validation, you will have to fix the “errors”, which, by good chance, may not coincide with the true problem. We can get anything.

    But if we look at neighboring objects, a lot can become clear:

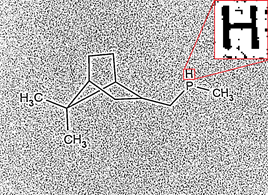
    And even if you have never encountered structural formulas in chemistry ever, but from this picture for some reason it becomes obvious that this is a connection (a line, a straight line or two straight lines with a rounded corner). We see the image of three symbols, we see how neat they are, we estimate their approximate size, we understand that the "rounded thing" is not a symbol.

    There is another option:

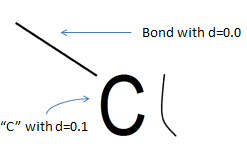
    We saw a line that is absolutely straight, we saw a “perfect” symbol standing next to it, our object is similar in size, although it is drawn less qualitatively. It is more difficult to say for sure here, but if we know that connections should connect objects, and there is nothing in the direction of the ends of our object, then it is hardly a connection. And if we recall that “Cl” (chlorine) is a very likely combination of symbols in our subject area, then yes, it is still the symbol “l”.

    Here I practically outlined in a free style sketches of the separation algorithm. And now more formally.

    Threshold part:
    • If in the metrics table for an object only one value is “good” (close to zero), and all the others differ by a minimum by constant C, then we mark it with the corresponding class.

    It’s great, but it’s not always like that.

    For the remaining objects, we resort to statistical analysis:
    • Determination of the average size of potential symbols and deviations from it;
    • Determination of the average length of potential lines, deviation from it;
    • Determination of the average curvature of potential lines;
    • Determination of the average thickness of lines, symbols;
    • And other statistical criteria, for example hu moments (which, by the way, OpenCV can count).

    We still don’t know for each object - what class it has, we simply look at the metrics table and select the object closest in value to it - this is what I put in the concept of " potential ".

    Then we build a classification tree, in the nodes of which the following conditions can be met: (if the height of the object lies in the range from mean_height_symbol-1 to mean_height_character + 2, while it has a curvature greater than 3 * mean_curvature_line and its length is less than 0.5 * average length of lines), then it It is marked as a symbol. The method of constructing classification trees is well described here , and I allow myself not to repeat it.

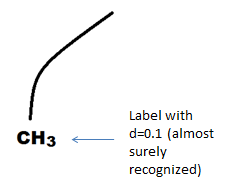
    After passing through the statistical part, some objects will be marked with hypothetical classes. In most practical cases, almost all objects. If we were unable to mark at least half of the objects, then most likely something went wrong with us (and this often happens for handwritten pictures). But we will not “despair” and simply select half of the objects with the smallest metric values ​​and mark them without taking into account statistical information (for this strange squiggle from the example, just look at the distance table, and if it is closer to “l”, we will assign it with the symbol “ l. ”What problems may arise in this case, I have already described, but this is a necessary solution).

    For the remaining objects, we apply a local analysis:
    • Find all the neighbors for the selected object;
    • If some of the neighbors already have the selected class, then we select from the probability table of local configurations the more probable one;
    • Additionally: if there are no other objects standing in the direction of the ends of the object, then it is a symbol.

    For the remaining objects, we select the class “by default” - the one that is closer in metric value.

    As a result of all the torment, we can divide the image into a set of objects that are supposedly symbols and the part responsible for the structure.


    Structural level


    Now it remains to assemble the finished structure from a set of elements. Here, of course, the algorithms themselves begin to depend heavily on the subject area.

    Without going into chemical details, in Imago OCR we work with images of molecules, which in fact represent a bond graph with vertices (labels) at the tops of them, so the very task of assembling the structure is quite trivial. But not every combination of symbols is a valid label of an atom, and it is not possible to construct a correct graph from any set of segments. Labels can use superscripts and superscripts, charge signs, and parenthesis sequences. For further discussion, I will choose the most interesting, and possibly potentially useful points.

    Structure graph processing

    The first important step is actually getting this graph. After vectorization, all we have is a set of disparate segments, each of which has a “beginning” and “end”, which I marked with circles in the image of the structure:

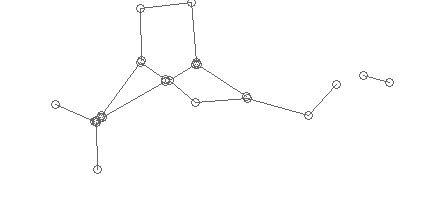
    We statistically determine the average radius of possible gluing, and “collect” the segments whose ends lie in this radius to the vertices of the graph:

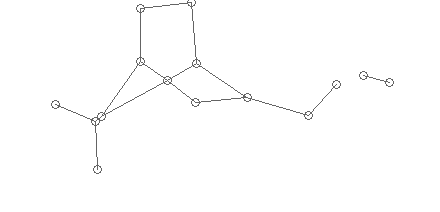
    The radius can be defined as follows - for each vertex calculate the minimum distance to the neighbors and find the peak of the histogram. If this peak gives a radius larger than the average size of the symbol, then we can assume that all segments are not connected.

    Then remove too short edges:

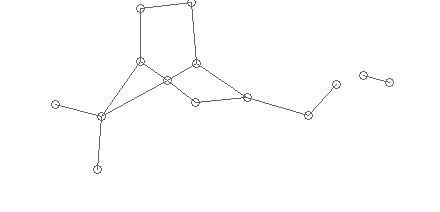
    Too short edges are the result of vectorization of lines with artifacts (bends, pixel noise). We have an average symbol size, we can assume that a bond length shorter than the symbol size is impossible (with a number of exceptions that are checked in a special way - chemical specificity).

    The above items will be useful in recognizing tables, for example. And we still have a search for multiple edges, finding "bridges" (a planar image of disjoint edges), finding the image of the "arrow". All this is much more convenient to do, working with the graph structure, and not with intermediate recognition results - you should not achieve "ideal" vectorization.

    Label assembly and processing

    For symbols, it is necessary to carry out grouping and here a solution similar to the “assembly" of the graph is applied. Each collected label must be recognized, and since there may be superscripts and subscripts - the task becomes more interesting.
    To begin with, the “baseline” of the label
    is calculated: This is a straight line (in fact, just a certain value of baseline_y), above which are the capital letters of the label, and under which are the indices. To determine baseline_y, statistics will help us:
    • determination of the average size of the uppercase character (for most characters, the spelling of uppercase and lowercase is different);
    • when analyzing each specific label, we select the average value of the y coordinate for all characters whose size is within the average.

    Why do we take the average, and not the maximum (the line should go under the label symbols)? So more stable; if we made a mistake in interpreting the symbol as capital, we can erroneously classify the index as capital, draw a line under it, and, accordingly, “we will no longer have indexes”. The choice of the middle one, on the one hand, does not significantly change the value of baseline_y in good cases, and on the other hand, the price of the error of the incorrect choice of capital letters falls.

    Then we recognize the characters, one by one. For each character we calculate:
    • % of its height under the baseline;
    • Relation to the average height of uppercase characters.

    The threshold decision regarding these parameters would be rather unfortunate: if at least 30% of the symbol is under the base line, then it is an index. And if 29? In general, the entire recognition process can be described as well as possible with the idea of ​​duck test. If something looks like an index, then most likely it is an index. And it looks like an index, if it looks like something else even less.

    What increases the likelihood of a character being an index? The smaller it is, and the lower it is relative to the baseline. And the numbers are more likely to be an index. One of the good ideas for recognition was to use a set of changes to the list of metrics (do you still remember that for each object we store all possible objects similar to it?). Now, interpretations as subscripts are also added to this set of metrics. These are the metric values ​​that were originally copied from ordinary values ​​during the recognition process change:
    • If a symbol lies k% below the baseline, then the metric for its interpretation as a lower index decreases f (k) times;
    • If a symbol is n% smaller in height than the average height, then the metric for its treatment as a..z symbol decreases by g (n) times.

    Accordingly, in the recognition process, after applying all the rules, we simply select the interpretation with the lowest metric value - this is the winning symbol, the most similar. But we still will not “forget” the other interpretations.

    Tag validation

    The next step after receiving ready-made interpretations of labels entirely is their validation. In each subject area, it has its own: for the Russian language, this is a check according to dictionaries, for a number of identifiers it can be checksums, and in chemistry a set of valid elements. To implement this particular part, we still have a complete set of alternatives for each object.

    Let our label consist of two characters: {c1, c2}
    Moreover, c1 is “Y” with a metric value of 0.1 and “X” with a metric value of 0.4;
    c2 is “c” with a metric value of 0.3 and “e” with a metric value of 0.8.
    I could just write that our label is Yc . But the Yc labelnot valid. To get a valid label, we can go through the possible alternatives and select a valid one. Among the valid ones, the one with the minimum metric value.
    In this case, out of all 4 options, only one " Xe " is valid , giving the final metric 1.2.

    It seems that we have solved the problem, now the label value is valid. But what if “Yc” was what the author of the picture wanted to use, contrary to correctness. In order to understand this, we subtract the new value of the metric (1.2) from the old (0.4), and interpret the resulting difference (0.8). It can be compared with a certain threshold, and prohibit correction if it exceeds it. But how to choose this threshold?

    Machine learning


    How do you choose the numerous constants, threshold restrictions used in the recognition process? Initial values, of course, can be chosen on the basis of common sense, but will they be optimal?

    The solution to such problems can be partially entrusted to the machine - to perform random changes in the parameters and choose those that give on average the best result. Random changes can be systematized using a modification of the genetic algorithm , which we did.

    But it should be understood that the recognition process from a computational point of view is a black box, and it can work indefinitely on some sets of parameters. To do this, we used runtime measurements and the limitation of those sets on which this time increased significantly. This approach has been shown to be effective in most cases.

    The topic deserves a separate note, but now, as a thesis, I will say that training a system assembled from adaptive functional blocks works much more efficiently than training a neural network based on threshold activation functions; there are fewer constants and each has a direct (and usually explainable) effect on the result. They could be chosen manually, but the relationship of the parameters, and their correct change after a partial change in the algorithms is a difficult task for a person.

    Instead of a conclusion


    Much remains "in the shadows" and the creation of an OCR system building guide is still a long way off, if at all with a similar goal. I would like it to be clear from the note what problems may arise, what possible solutions exist, and that there is a significant difference between the character recognition algorithm and the construction of a complete optical recognition system for structural information. I will be glad to constructive criticism and suggestions to supplement the notes.

    In addition, if it will be interesting to implement the methods described in the note, I will duplicate the link to the open-source project Imago OCR , discussion and suggestions for the development of which are welcomed in the corresponding google group .
    Tags:

    Also popular now: