Differential Evolution: Genetic Function Optimization Algorithm
On Habré there are many articles on evolutionary algorithms in general and genetic algorithms in particular. Such articles usually describe the general structure and ideology of the genetic algorithm in more or less detail, and then give an example of its use. Each such example includes some version of the procedure of crossing individuals, mutation and selection chosen by the author, and in most cases for each new task you have to come up with your own version of these procedures. By the way, even the choice of representing the element of the decision space by the gene vector greatly affects the quality of the resulting algorithm and is essentially an art.
At the same time, many practical problems can easily be reduced to the optimization problem of finding the minimum of the function nmaterial variables, and for such a typical variant, I would like to have a ready-made reliable genetic algorithm. Since even the determination of the cross and mutation operators for vectors consisting of real numbers is not entirely trivial, the “production” of a new algorithm for each such task is especially time-consuming.
Under the cut is a brief description of one of the most famous genetic algorithms for material optimization - the differential evolution algorithm (Differential Evolution, DE). For complex problems of optimizing the function of n variables, this algorithm has such good properties that it can often be considered as a ready-made “building block” for solving many problems of identification and pattern recognition.
I will assume that the reader is familiar with the basic concepts used in the description of genetic algorithms, therefore I will immediately turn to the essence of the matter, and in conclusion I will describe the most important properties of the DE algorithm.
A random set of N vectors from the space R n is selected as the initial population . The distribution of the initial population should be selected based on the characteristics of the optimization problem being solved — usually a sample is used from an n- dimensional uniform or normal distribution with given mathematical expectation and dispersion.
At the next step of the algorithm is made crossing each individual X from the initial population of randomly chosen individual of the C , different from X . The coordinates of vectors X and C are considered as genetic traits. Before crossing used special operator mutations - in the cross involves not original and distorted genetic traits individuals the C :

where A and Bed and - randomly selected representatives of the population, different from X and the C . The parameter F determines the so-called mutation strength- the amplitude of the disturbances introduced into the vector by external noise. It should be noted that the noise distorting the “gene pool” of an individual C is not an external source of entropy, but an internal source - the difference between randomly selected representatives of the population. Below we dwell on this feature in more detail.
Crossing is as follows. Given the probability P , which descendant T inherits another (distorted mutation) genetic trait from the parent C . Relevant features of the parent X inherited with probability 1 - P . In fact, a binary random variable with mathematical expectation P is played out n timesAnd its values for single inheritance is performed (transfer) by distorted genetic trait parent C (i.e., corresponding to the coordinates of the vector C ' ), while for zero values - genetic trait inheritance from the parent X . As a result, a descendant vector T is formed .
Selection is carried out at each step of the functioning of the algorithm. After the formation of progeny vectors T compares goal function for him and his "direct" parent X . The one of the vectors X and T is transferred to the new population , on which the objective function reaches a lower value (we are talking about the minimization problem). It should be noted here that the described selection rule guarantees the invariability of the size of the population during the operation of the algorithm.
In general, the DE algorithm is one of the possible “continuous” modifications of the standard genetic algorithm. At the same time, this algorithm has one significant feature that largely determines its properties. In the DE algorithm, the source of noise is not an external random number generator, but an “internal” one, implemented as the difference between randomly selected vectors of the current population. Recall that a set of random points selected from a certain general distribution is used as the initial population. At each step, the population is transformed according to certain rules, and as a result, at the next step, a set of random points is again used as a noise source, but a new distribution law corresponds to these points. Experiments show that in general, the evolution of the population corresponds to the dynamics of the “swarm of midges” (ie, a random cloud of points) moving as a whole along the relief of the optimized function, repeating its characteristic features. In case of falling into the ravine, the “cloud” takes the form of this ravine and the distribution of points becomes such that the mathematical expectation of the difference of two random vectors is directed along the long side of the ravine. This ensures rapid movement along narrow elongated ravines, whereas gradient methods under similar conditions are characterized by vibrational dynamics “from wall to wall”. The given heuristic considerations illustrate the most important and attractive feature of the DE algorithm - the ability to dynamically model the terrain features of the optimized function, adjusting the distribution of the “built-in” noise source for them.
For population size N , Q * n is usually recommended , where 5 <= Q <= 10 .
For the mutation strength F, reasonable values are selected from the interval [0.4, 1.0] , with 0.5 being a good initial value , but with fast degeneration of the population far from the solution, the parameter F should be increased .
The probability of mutation P varies from 0.0 to 1.0 , and it should begin with relatively large values ( 0.9 or even 1.0) to check the possibility of quickly obtaining a solution by random search. Then, the parameter values should be reduced to 0.1 or even 0.0 , when practically no variability is introduced into the population and the search is convergent.
Convergence is most affected by population size and the strength of the mutation, and the probability of mutation serves to fine tune.
The features of the DE method are well illustrated when it is run on the standard Rosenbrock test function of the form

This function has an obvious minimum at x = y = 1 , which lies at the bottom of a long winding ravine with steep walls and a very flat bottom.
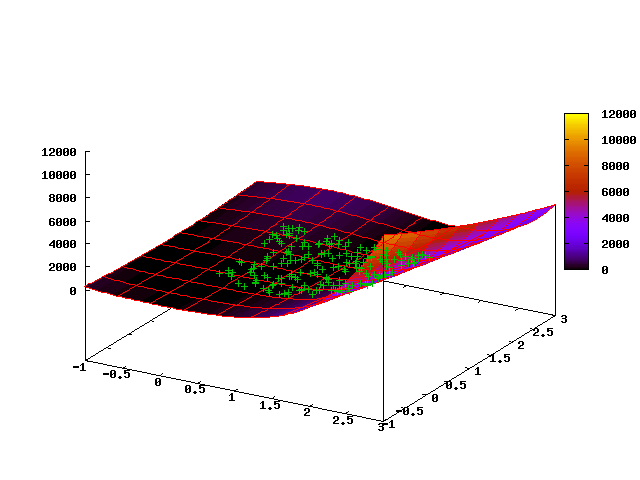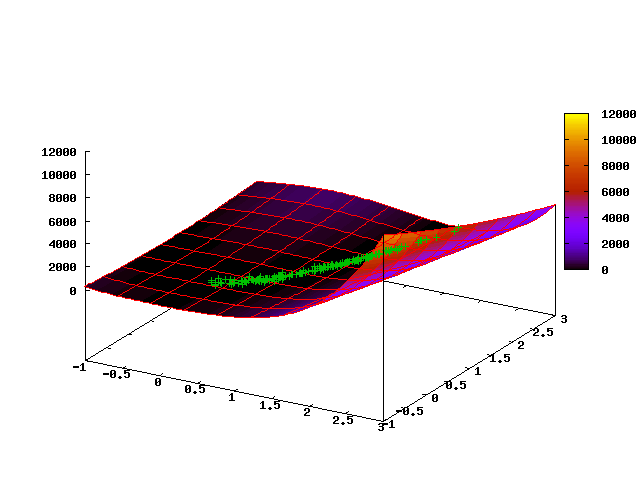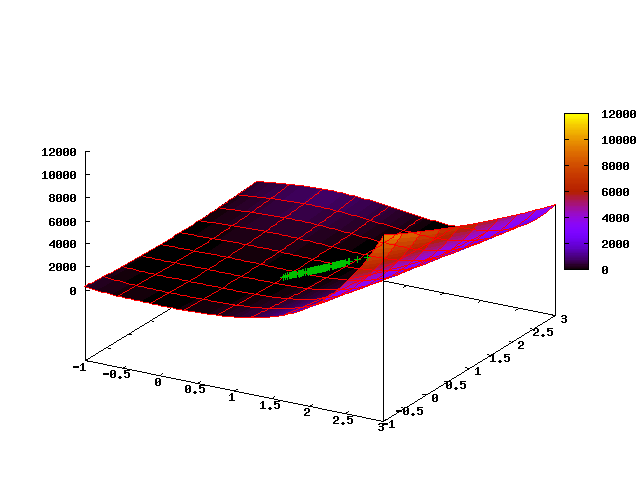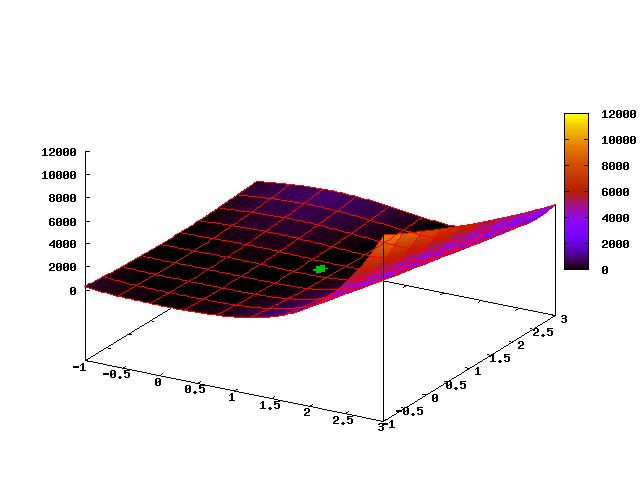
When starting with a uniform initial distribution of 200 points in the square [0, 2] x [0, 2] after 15 steps, we get the following distribution of the population:

It can be seen that the “cloud” of points is located along the bottom of the ravine and most mutations will also lead to a shift of points along the bottom of the ravine, i.e. the method adapts well to the features of the geometry of the space of solutions.
The following animated picture shows the evolution of a point cloud in the first 35 steps of the algorithm (the first frame corresponds to the initial uniform distribution):
At the same time, many practical problems can easily be reduced to the optimization problem of finding the minimum of the function nmaterial variables, and for such a typical variant, I would like to have a ready-made reliable genetic algorithm. Since even the determination of the cross and mutation operators for vectors consisting of real numbers is not entirely trivial, the “production” of a new algorithm for each such task is especially time-consuming.
Under the cut is a brief description of one of the most famous genetic algorithms for material optimization - the differential evolution algorithm (Differential Evolution, DE). For complex problems of optimizing the function of n variables, this algorithm has such good properties that it can often be considered as a ready-made “building block” for solving many problems of identification and pattern recognition.
I will assume that the reader is familiar with the basic concepts used in the description of genetic algorithms, therefore I will immediately turn to the essence of the matter, and in conclusion I will describe the most important properties of the DE algorithm.
Initial population generation
A random set of N vectors from the space R n is selected as the initial population . The distribution of the initial population should be selected based on the characteristics of the optimization problem being solved — usually a sample is used from an n- dimensional uniform or normal distribution with given mathematical expectation and dispersion.
Reproduction of descendants
At the next step of the algorithm is made crossing each individual X from the initial population of randomly chosen individual of the C , different from X . The coordinates of vectors X and C are considered as genetic traits. Before crossing used special operator mutations - in the cross involves not original and distorted genetic traits individuals the C :

where A and Bed and - randomly selected representatives of the population, different from X and the C . The parameter F determines the so-called mutation strength- the amplitude of the disturbances introduced into the vector by external noise. It should be noted that the noise distorting the “gene pool” of an individual C is not an external source of entropy, but an internal source - the difference between randomly selected representatives of the population. Below we dwell on this feature in more detail.
Crossing is as follows. Given the probability P , which descendant T inherits another (distorted mutation) genetic trait from the parent C . Relevant features of the parent X inherited with probability 1 - P . In fact, a binary random variable with mathematical expectation P is played out n timesAnd its values for single inheritance is performed (transfer) by distorted genetic trait parent C (i.e., corresponding to the coordinates of the vector C ' ), while for zero values - genetic trait inheritance from the parent X . As a result, a descendant vector T is formed .
Selection
Selection is carried out at each step of the functioning of the algorithm. After the formation of progeny vectors T compares goal function for him and his "direct" parent X . The one of the vectors X and T is transferred to the new population , on which the objective function reaches a lower value (we are talking about the minimization problem). It should be noted here that the described selection rule guarantees the invariability of the size of the population during the operation of the algorithm.
Discussion of the features of the DE algorithm
In general, the DE algorithm is one of the possible “continuous” modifications of the standard genetic algorithm. At the same time, this algorithm has one significant feature that largely determines its properties. In the DE algorithm, the source of noise is not an external random number generator, but an “internal” one, implemented as the difference between randomly selected vectors of the current population. Recall that a set of random points selected from a certain general distribution is used as the initial population. At each step, the population is transformed according to certain rules, and as a result, at the next step, a set of random points is again used as a noise source, but a new distribution law corresponds to these points. Experiments show that in general, the evolution of the population corresponds to the dynamics of the “swarm of midges” (ie, a random cloud of points) moving as a whole along the relief of the optimized function, repeating its characteristic features. In case of falling into the ravine, the “cloud” takes the form of this ravine and the distribution of points becomes such that the mathematical expectation of the difference of two random vectors is directed along the long side of the ravine. This ensures rapid movement along narrow elongated ravines, whereas gradient methods under similar conditions are characterized by vibrational dynamics “from wall to wall”. The given heuristic considerations illustrate the most important and attractive feature of the DE algorithm - the ability to dynamically model the terrain features of the optimized function, adjusting the distribution of the “built-in” noise source for them.
Selection of parameters
For population size N , Q * n is usually recommended , where 5 <= Q <= 10 .
For the mutation strength F, reasonable values are selected from the interval [0.4, 1.0] , with 0.5 being a good initial value , but with fast degeneration of the population far from the solution, the parameter F should be increased .
The probability of mutation P varies from 0.0 to 1.0 , and it should begin with relatively large values ( 0.9 or even 1.0) to check the possibility of quickly obtaining a solution by random search. Then, the parameter values should be reduced to 0.1 or even 0.0 , when practically no variability is introduced into the population and the search is convergent.
Convergence is most affected by population size and the strength of the mutation, and the probability of mutation serves to fine tune.
Numerical example
The features of the DE method are well illustrated when it is run on the standard Rosenbrock test function of the form

This function has an obvious minimum at x = y = 1 , which lies at the bottom of a long winding ravine with steep walls and a very flat bottom.
When starting with a uniform initial distribution of 200 points in the square [0, 2] x [0, 2] after 15 steps, we get the following distribution of the population:

It can be seen that the “cloud” of points is located along the bottom of the ravine and most mutations will also lead to a shift of points along the bottom of the ravine, i.e. the method adapts well to the features of the geometry of the space of solutions.
The following animated picture shows the evolution of a point cloud in the first 35 steps of the algorithm (the first frame corresponds to the initial uniform distribution):

References
- The homepage of the algorithm contains many implementations and examples of use in various fields.
- Article in Dr. Dobb's Journal contains a very simple and understandable implementation in C, which can be taken as a basis when using the DE algorithm in your projects.
