Let math fold hearts

One and one - it turns out two. All are alone - here you are, and there I am.
People are always doubly alone with themselves alone.
If something could bring them closer together, just one of the two would turn out to be one.
Let mathematics add hearts - to make our way to the end.

Williams Jay, Heroes of Nowhere

Probably, the post should be titled "How to draw an animated heart for Valentine's Day, using math for other purposes." I rejected this name in favor of a more poetic one: after all, a wonderful romantic holiday is approaching, which we, IT specialists and other nerds, should meet fully armed. I will immediately show you the result, and under the habrakat there will be many letters about how I achieved this result.

Disclaimer

I realize that a beautiful blinking heart can be made without the slightest knowledge of mathematics. But is it really interesting?

Step 1. Parameterize the heart.

To begin with, we need a mathematical object, at least remotely resembling a heart. Fortunately, for me this step was trivial: a couple of years ago I discovered a wonderful formula just for such a case (for aesthetic reasons, the graph in the figure is stretched horizontally, in fact, it should fit between -1 and 1).



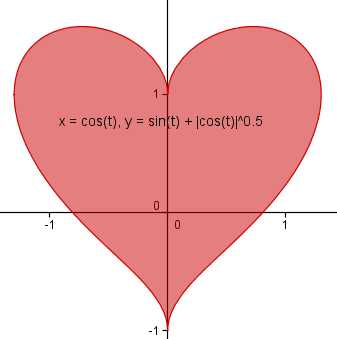
The formula was discovered from the following considerations: take an ordinary circle (x = cos (t); y = sin (t))and imagine that it consists of jelly, while being firmly attached to the y-axis. Now we “blow” to it from below: we add to the coordinate of the game a certain function w (x) = w (x (t)), which is equal to zero at x = 0, monotonically increasing at x> 0 and even in x. After such a “blow”, the halves of the circle will shift upward, forming a “bulge” of the heart, and due to the rigid attachment to the Y axis, a lower “tail” and an upper “dent” will form. In this case, w (x (t)) = | x | ^1/2 = | cos (t) | ^1/2 . You can try another “blow function” yourself and see what comes of it.

Step 2. From a parametric job to an implicit function.

For our insidious plan, the parametric equation (x (t); y (t)) is inconvenient; an implicit assignment of the form f (x, y) = 0 would be preferable. Well, everything is in our hands. So, the pants turn:

x = cos (t)
y = sin (t) + | cos (t) | ^1/2
y - | x | ^1/2 = sin (t)
(y - | x | ^1/2 ) ² + x ² = 1
f (x, y) = (y - | x | ^1/2 ) ² + x ² - 1 = 0

Step 3. From an implicit function to a function of two variables. Color function.

With f (x, y) on hand, we can finally fulfill our dream: to draw a beautiful color picture. To do this, we need another function: the color function. It should take a real argument r and return an integer value from 0 to 255. It is also desirable that it be monotonous on each axis and have a maximum at zero. As such a function, you can take, for example, this:

c (r) = max ([255 - 100 * | r |], 0)

Here 100 is a “magic number”, later we will replace it in full accordance with the “good programming style” with a parameter.
Now for each point (x, y) we can set the color as rgb (c (f (x, y)), 0, 0). Those points that used to belong directly to the “heart” chart turned bright red (pay attention to the motionless light outline on the gif). As you move away from the graph, the color will fade until it turns black at some distance from it.

Step 4. Add a parameter, create an animation.

Now replace the magic number 100 with the parameter k. The new color feature looks like this:

c (r, k) = max ([255 - k * | r |], 0)

Let k be a function of time. Then for each point in the image at each moment in time we can calculate its color (which is, in fact, the mathematical definition of animation). At first I wanted to take something like k (t) = 80 (sin (t) +1). Then, however, I realized that with a large number of frames, the gif will weigh more than 640 kilobytes. On the other hand, with a small number of frames, it makes no sense to bother with the analytical task k (t). As a result, in order to achieve a pulsating heart, I sequentially assigned k values ​​of 80, 90, 100, 110, 120, 110, 100, 90, and then combined the images generated for these values ​​into a cyclic GIF. In general, that's all.

Conclusion

Unfortunately, I could not arrange a surprise for my girlfriend: she insidiously crept up behind me just when I generated frames for animation. However, she liked it.
Artists, designers and other comrades with a heightened sense of beauty will surely say that the heart could have been more beautiful. In part, I agree with them: the picture is not without flaws. However, its true beauty lies in mathematical rigor. My girlfriend appreciated it. And you?